Аналитическая статистика.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Выборочное наблюдение презентация
Содержание
- 1. Выборочное наблюдение
- 2. 2 Выборочное наблюдение Под выборочным наблюдением понимается
- 3. 3 Выборочное наблюдение
- 4. 4 Ошибка выборочного наблюдения Ошибка выборочного наблюдения
- 5. 5 Теорема П.Л.Чебышева При достаточно большом числе
- 6. 6 Теорема А.М.Ляпунова Распределение выборочных средних (а
- 7. 7 Теорема А.М.Ляпунова Значение интеграла F(t) для
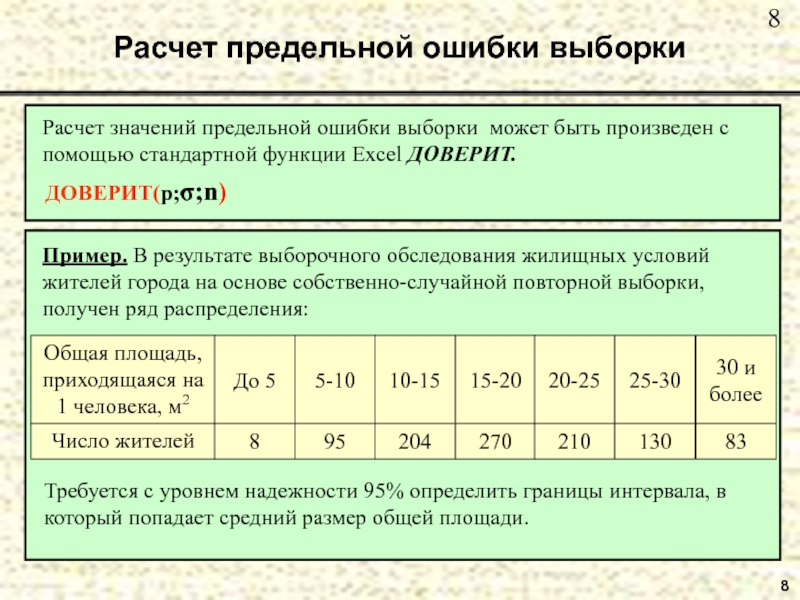
- 8. 8 Расчет предельной ошибки выборки
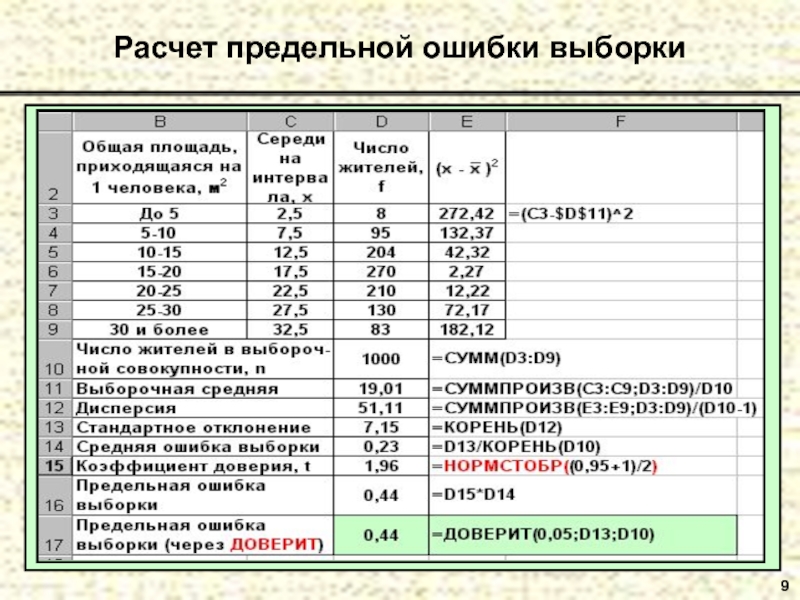
- 9. 9 Расчет предельной ошибки выборки
- 10. 10 Теорема Бернулли
- 11. 11 Теорема Бернулли
- 12. 12 Уточнение формулы средней ошибки выборки
- 13. 13 Уточнение формулы средней ошибки выборки Для
- 14. 14 Предельная ошибка альтернативного признака Для приведенного
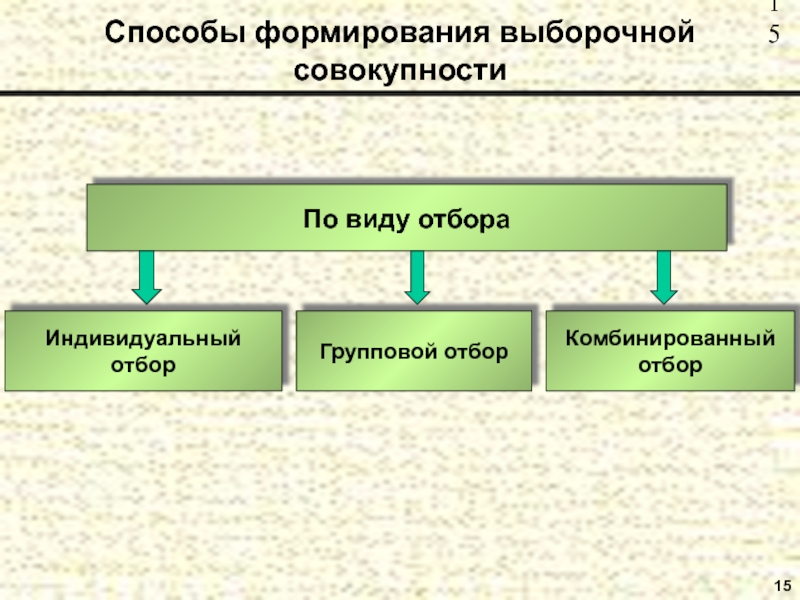
- 15. 15 Способы формирования выборочной совокупности По виду отбора
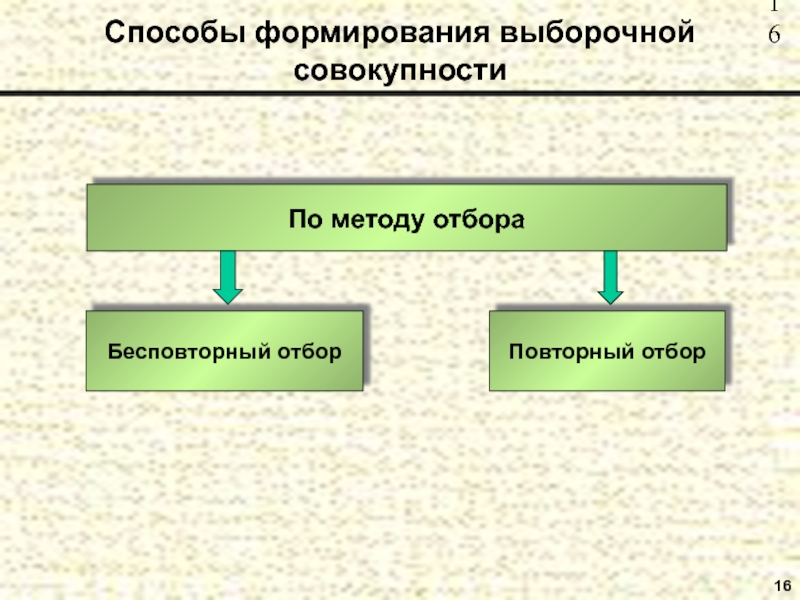
- 16. 16 Способы формирования выборочной совокупности По методу отбора
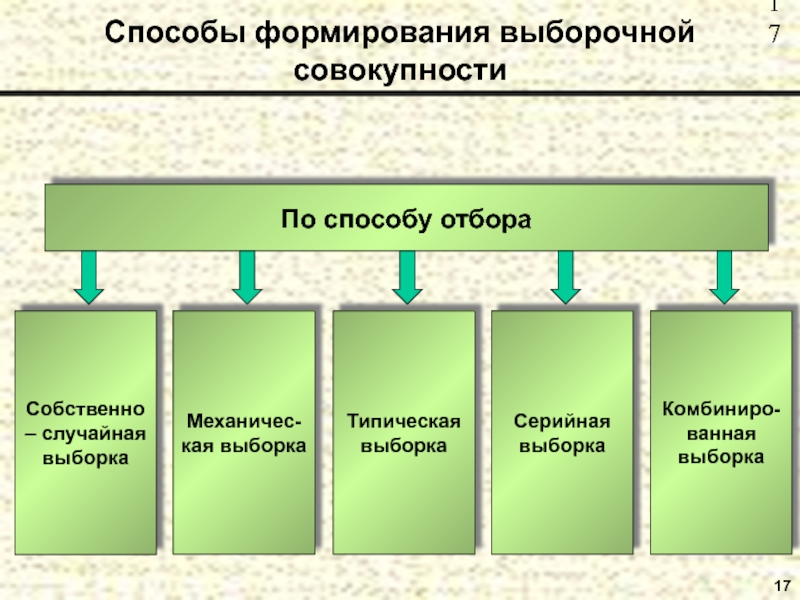
- 17. 17 Способы формирования выборочной совокупности По способу отбора
- 18. Типическая выборка 18
- 19. Типическая выборка 19 Пример. 10%-ный бесповторный
- 20. 20 Типическая выборка 1. Расчет пропорционально объему типических групп.
- 21. 21 Типическая выборка 2. Расчет пропорционально дифференциации признака.
- 22. 22 Серийная выборка Средняя ошибки выборки: повторный отбор бесповторный отбор Межгрупповая дисперсия:
- 23. Определение необходимого объема выборки 23
- 24. 24 Определение необходимого объема выборки
- 25. 25 Определение необходимого объема выборки
- 26. 26 Определение необходимого объема выборки Пример
- 27. 27 Определение необходимого объема выборки Пример
- 28. 28 Малая выборка Распределение Стьюдента Под
- 29. 29 Способы нахождения критерия Стьюдента. 1.
- 30. 30 Малая выборка Распределение Стьюдента
- 31. 31 Малая выборка Распределение Стьюдента Пример.
Слайд 1Автор: Равичев Л.В.
РХТУ им. Д.И.Менделеева
Кафедра управления технологическими инновациями
Москва - 2013
СТАТИСТИКА
Лекция
Слайд 22
Выборочное наблюдение
Под выборочным наблюдением понимается такое несплошное наблюдение, при котором статистическому
Совокупность отобранных для обследования единиц в статистике принято называть выборочной, а совокупность единиц, из которых производится отбор, - генеральной.
Слайд 44
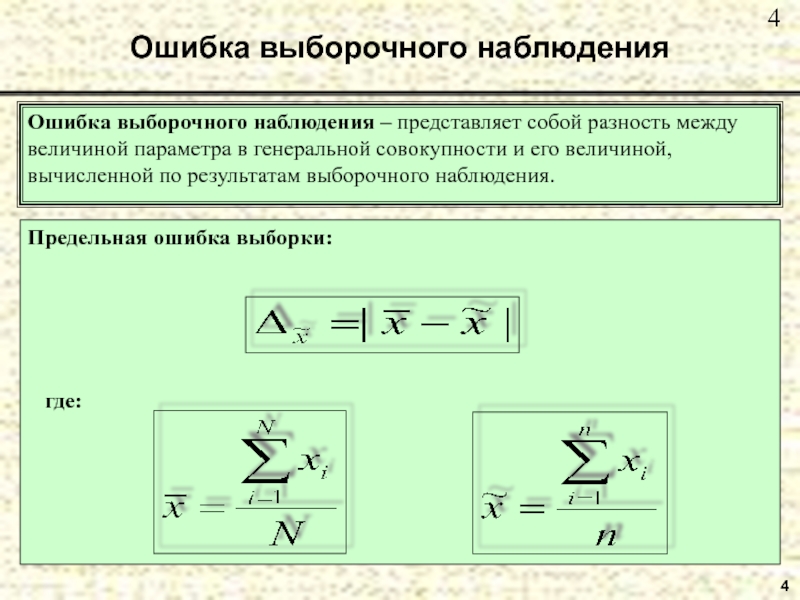
Ошибка выборочного наблюдения
Ошибка выборочного наблюдения – представляет собой разность между величиной
Слайд 55
Теорема П.Л.Чебышева
При достаточно большом числе независимых наблюдений с вероятностью, близкой к
Слайд 66
Теорема А.М.Ляпунова
Распределение выборочных средних (а следовательно, и их отклонений от генеральной
Предельная ошибка выборки дает возможность выяснить, в каких преде-лах находится величина генеральной средней.
Слайд 77
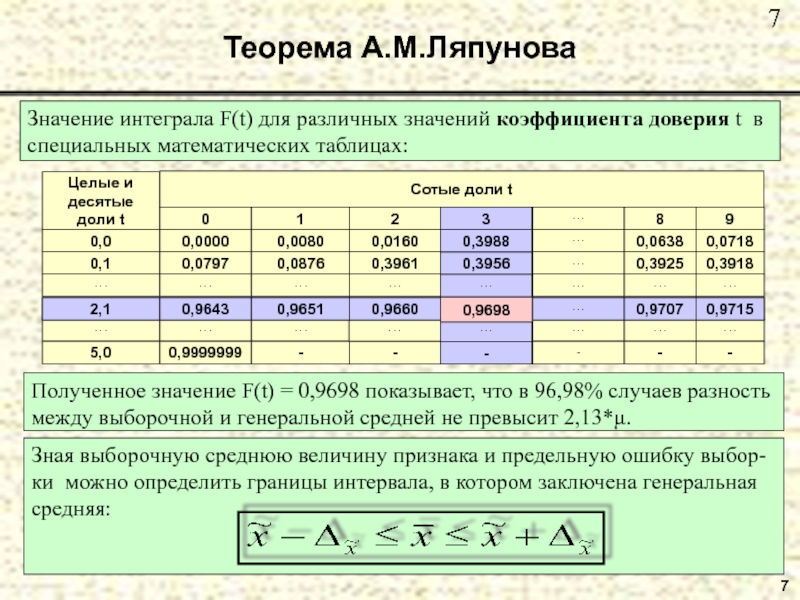
Теорема А.М.Ляпунова
Значение интеграла F(t) для различных значений коэффициента доверия t в
Полученное значение F(t) = 0,9698 показывает, что в 96,98% случаев разность между выборочной и генеральной средней не превысит 2,13*μ.
Слайд 1313
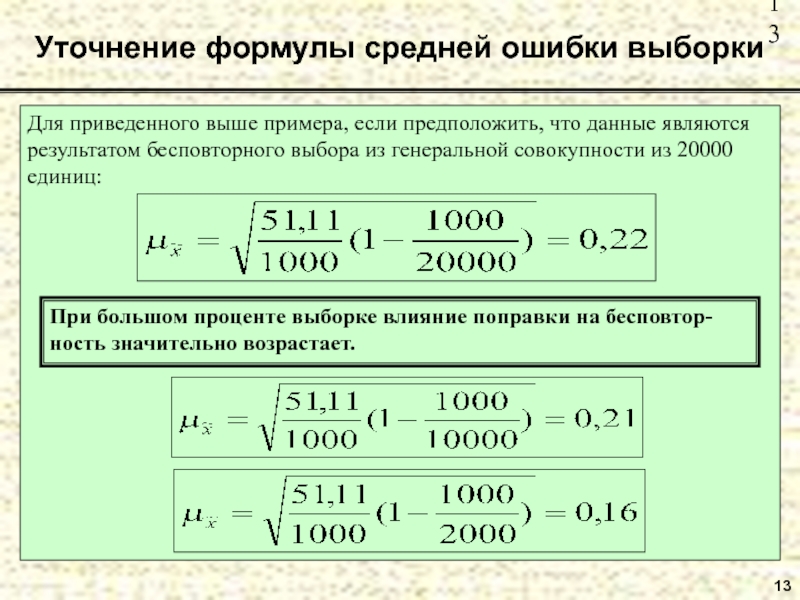
Уточнение формулы средней ошибки выборки
Для приведенного выше примера, если предположить, что
При большом проценте выборке влияние поправки на бесповтор-ность значительно возрастает.
Слайд 1414
Предельная ошибка альтернативного признака
Для приведенного выше примера, определим предельную ошибку выборки
1. Выборочная доля:
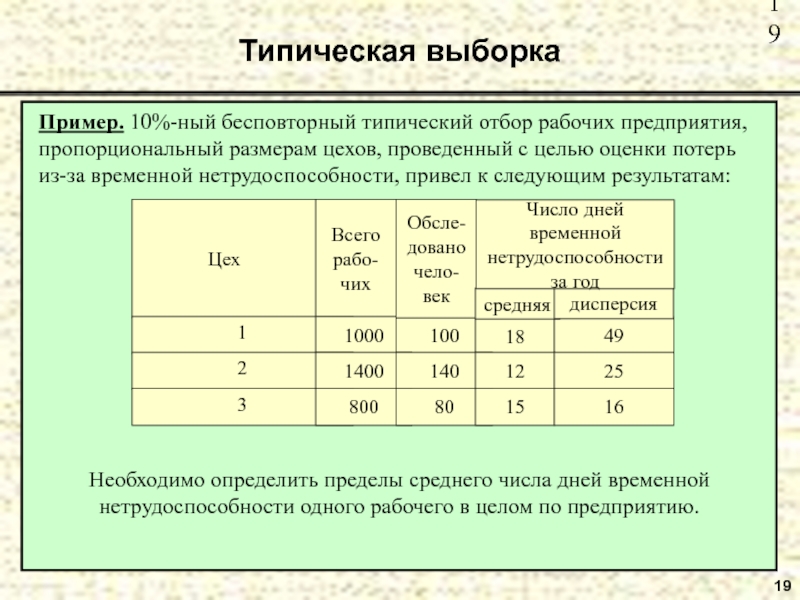
Слайд 19Типическая выборка
19
Пример. 10%-ный бесповторный типический отбор рабочих предприятия, пропорциональный размерам цехов,
Необходимо определить пределы среднего числа дней временной нетрудоспособности одного рабочего в целом по предприятию.
Слайд 2222
Серийная выборка
Средняя ошибки выборки:
повторный отбор
бесповторный отбор
Межгрупповая дисперсия:
Слайд 2626
Определение необходимого объема выборки
Пример 3. В фермерских хозяйствах области 10 000
Слайд 2727
Определение необходимого объема выборки
Пример 4. На склад поступило 100 ящиков деталей
Методики, разработанные в рамках конкретных обследований и опре-деленных способов формирования выборочной совокупности, требу-ют дальнейшего теоретического обоснования и практической провер-ки.
Слайд 2828
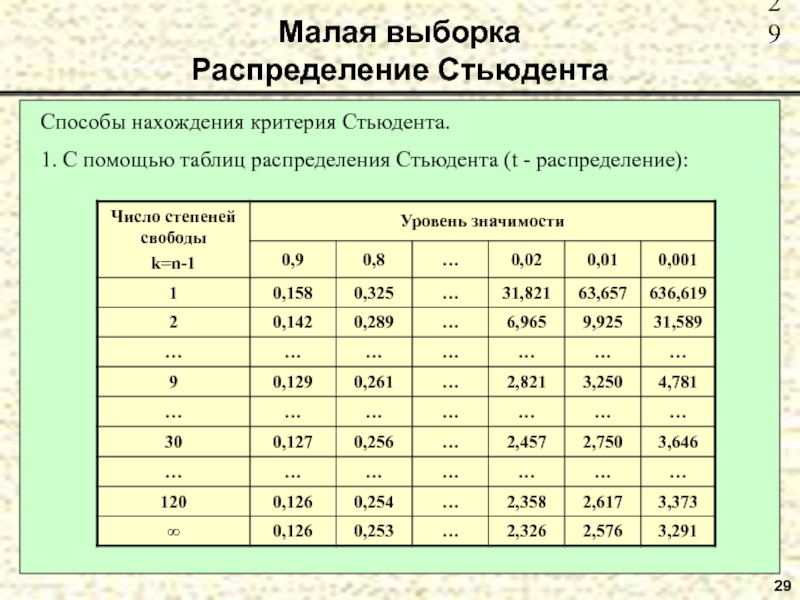
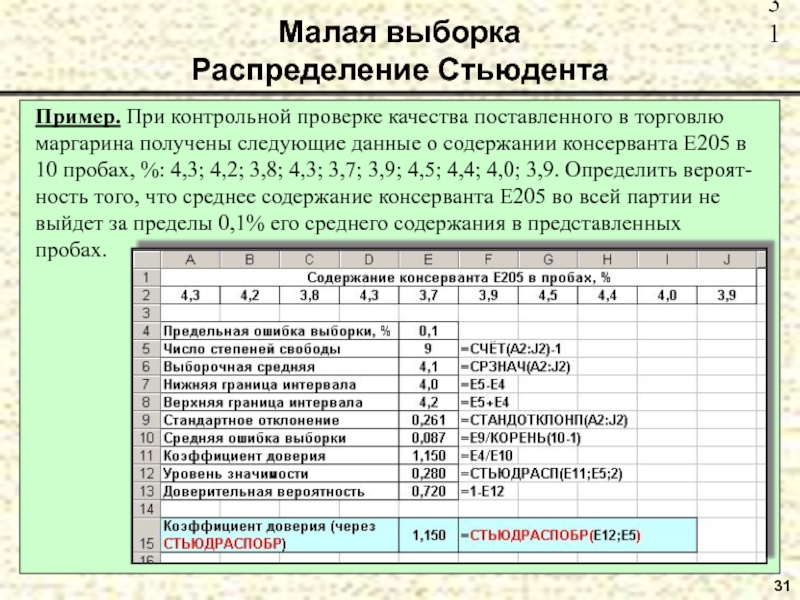
Малая выборка
Распределение Стьюдента
Под малой выборкой понимается такое выборочное наблюдение, числен-ность единиц
Критерий Стьюдента:
где:
мера случайных колебаний выборочной средней в малой выборке.
Слайд 2929
Способы нахождения критерия Стьюдента.
1. С помощью таблиц распределения Стьюдента (t -
Малая выборка
Распределение Стьюдента