- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Площади фигур презентация
Содержание
- 1. Площади фигур
- 2. Тема проекта: «Площади фигур»
- 3. Тип проекта: Информационный
- 4. Цель проекта: « Ознакомиться с формулами по нахождению площади в разных фигурах».
- 6. З а
- 7. Формулы площади треугольника 1)Формула площади треугольника
- 9. Формулы площади квадрата 1)Формула площади квадрата
- 10. Задача Найти площадь квадрата
- 11. Формула площади прямоугольника Площадь прямоугольника равна произведению
- 12. Задача Найти площадь прямоугольника.
- 13. Формулы площади
- 14. Задача Найти площадь параллелограмма Дано:
- 15. Формулы площади ромба 1)Формула площади ромба
- 16. Задача Найти площадь ромба
- 17. Формулы площади трапеции 1)Формула Герона для
- 18. Задача Найти площадь трапеции Дано:
- 19. Формулы площади выпуклого четырехугольника 1)Формула площади
- 20. Задача Найти площадь выпуклого четырехугольника
- 21. Формулы площади круга 1)Формула площади круга
- 22. Задача Найти площадь круга
- 23. Формулы площади эллипса Площадь эллипса равна
- 24. Задача Найти площадь эллипса
- 25. The END
Слайд 6 З а д а ч и п
А) Познакомиться с формулами S треугольника
Б)Познакомиться с формулами S квадрата
В)Познакомиться с формулами S прямоугольника
Г)Познакомиться с формулами S параллелограмма
Д)Познакомиться с формулами S ромба
Е) Познакомиться с формулами S трапеции
Ж) Познакомиться с формулами S
Выпуклого четырехугольника
З) Познакомиться с формулами S
круга
И) Познакомиться с формулами S
эллипса
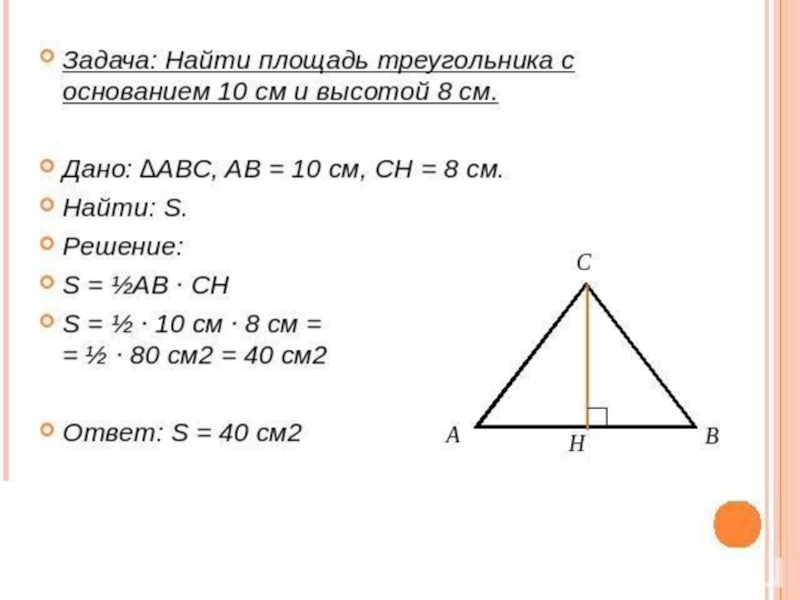
Слайд 7Формулы площади треугольника
1)Формула площади треугольника по стороне и высоте
Площадь треугольника равна
2)Формула площади треугольника по трем сторонам Формула Герона
S = √p(p - a)(p - b)(p - c)
3)Формула площади треугольника по двум сторонам и углу между ними Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними. S = 1/2 a · b · sin γ
4)Формула площади треугольника по трем сторонам и радиусу описанной окружности S = (a · b · с)/4R
5)Формула площади треугольника по трем сторонам и радиусу вписанной окружности Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности. S = p · r где S - площадь треугольника, a, b, c - длины сторон треугольника, h - высота треугольника, γ - угол между сторонами a и b, r - радиус вписанной окружности, R - радиус описанной окружности, p = (a + b + c) /2 - полупериметр треугольника.
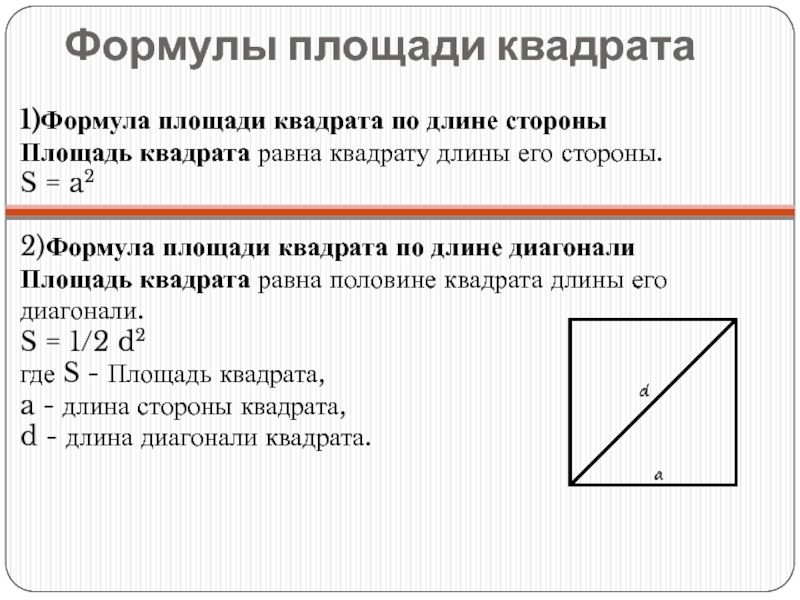
Слайд 9Формулы площади квадрата
1)Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины
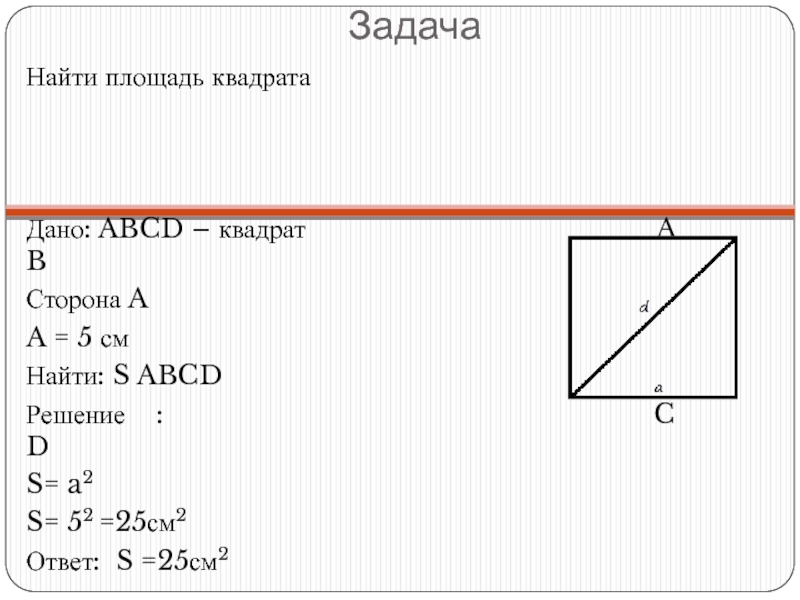
Слайд 10Задача
Найти площадь квадрата
Дано: ABCD – квадрат
Сторона A
A = 5 см
Найти: S ABCD
Решение : C D
S= a2
S= 52 =25см2
Ответ: S =25см2
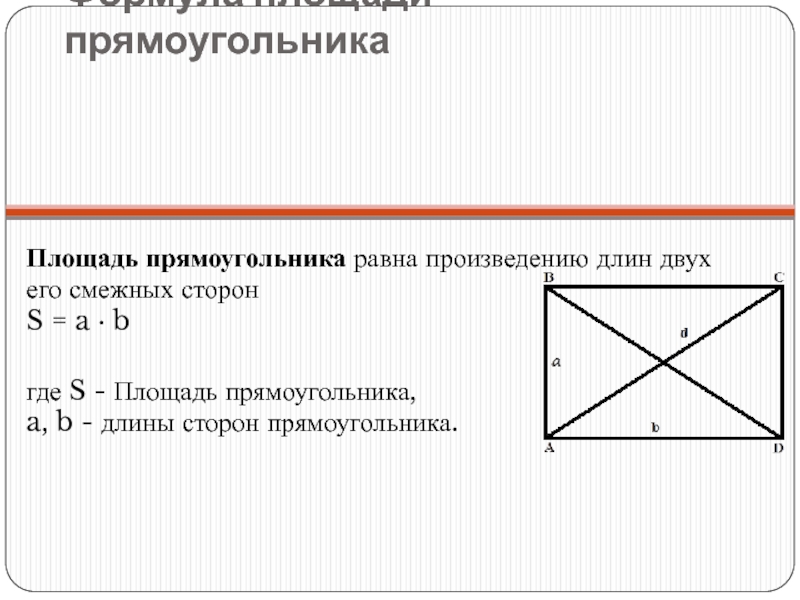
Слайд 11Формула площади прямоугольника
Площадь прямоугольника равна произведению длин двух его смежных сторон
S = a · b
где S
Слайд 12Задача
Найти площадь прямоугольника.
Дано: прямоугольник со сторонами a и b,
a = 4
Найти: S.
Решение:
S = ab
S = 4 см ∙ 2 см = 8 см2
Ответ: S = 8 см2
Слайд 13
Формулы площади параллелограмма
1)Формула площади параллелограмма по длине стороны и высоте
Площадь
2)Формула площади параллелограмма по двум сторонам и углу между ними Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними. S = a · b · sin α
3)Формула площади параллелограмма по двум диагоналям и углу между ними Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними. S = 1/2 d1 d2 · sin γ где S - Площадь параллелограмма, a, b - длины сторон параллелограмма, h - длина высоты параллелограмма, d1, d2 - длины диагоналей параллелограмма, α - угол между сторонами параллелограмма, γ - угол между диагоналями параллелограмма.
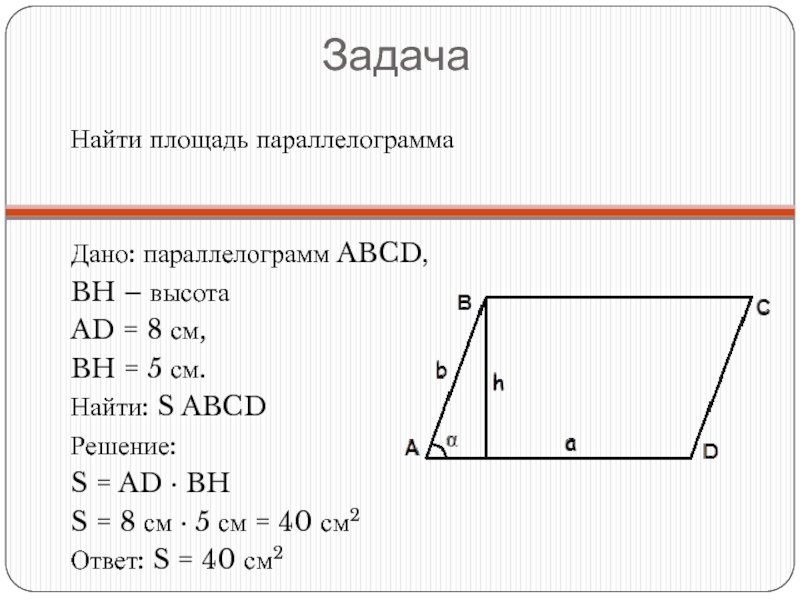
Слайд 14Задача
Найти площадь параллелограмма
Дано: параллелограмм ABCD,
BH – высота
AD = 8 см,
BH = 5 см.
Найти: S ABCD
Решение:
S = AD ∙ BH
S = 8 см ∙ 5 см = 40 см2
Ответ: S = 40 см2
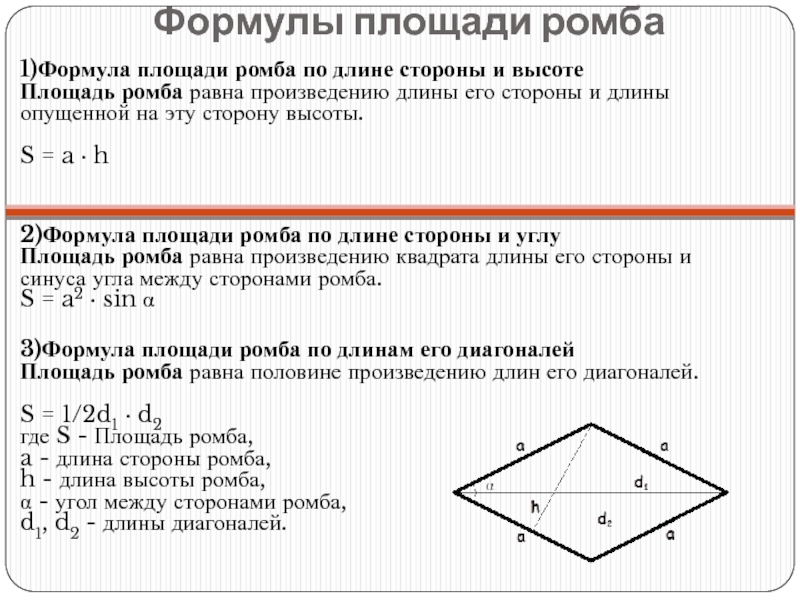
Слайд 15Формулы площади ромба
1)Формула площади ромба по длине стороны и высоте
Площадь ромба равна
2)Формула площади ромба по длине стороны и углу Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба. S = a2 · sin α
3)Формула площади ромба по длинам его диагоналей Площадь ромба равна половине произведению длин его диагоналей. S = 1/2d1 · d2 где S - Площадь ромба, a - длина стороны ромба, h - длина высоты ромба, α - угол между сторонами ромба, d1, d2 - длины диагоналей.
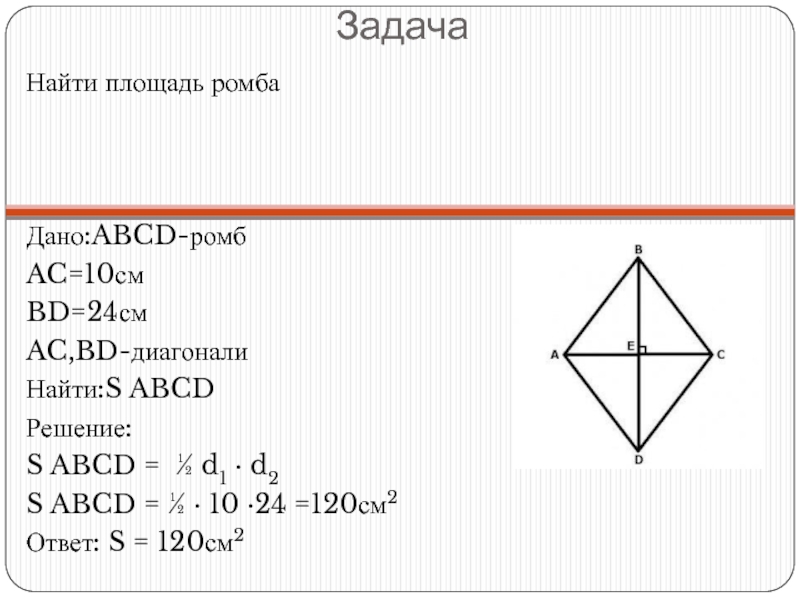
Слайд 16Задача
Найти площадь ромба
Дано:ABCD-ромб
AC=10см
BD=24см
AC,BD-диагонали
Найти:S ABCD
Решение:
S ABCD = ½ d1 · d2
S ABCD = ½ ·
Ответ: S = 120см2
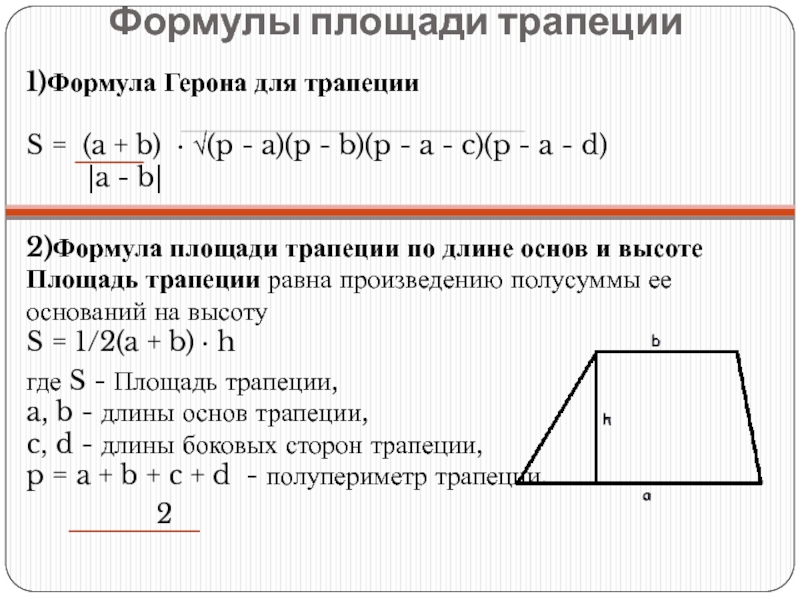
Слайд 17Формулы площади трапеции
1)Формула Герона для трапеции
S = (a + b) · √(p - a)(p - b)(p - a - c)(p - a - d)
2)Формула площади трапеции по длине основ и высоте Площадь трапеции равна произведению полусуммы ее оснований на высоту S = 1/2(a + b) · h
где S - Площадь трапеции, a, b - длины основ трапеции, c, d - длины боковых сторон трапеции, p = a + b + c + d - полупериметр трапеции.
2
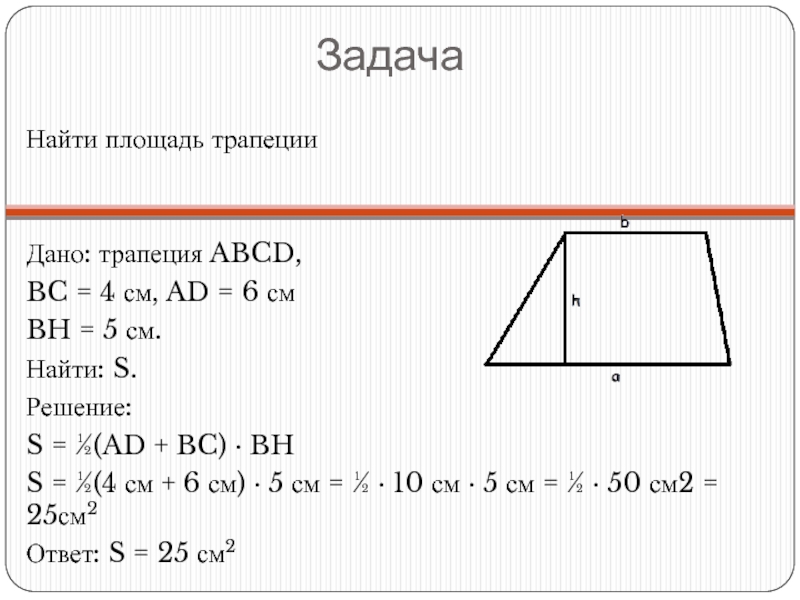
Слайд 18Задача
Найти площадь трапеции
Дано: трапеция ABCD,
BC = 4 см, AD =
BH = 5 см.
Найти: S.
Решение:
S = ½(AD + BC) ∙ BH
S = ½(4 см + 6 см) ∙ 5 см = ½ ∙ 10 см ∙ 5 см = ½ ∙ 50 см2 = 25см2
Ответ: S = 25 см2
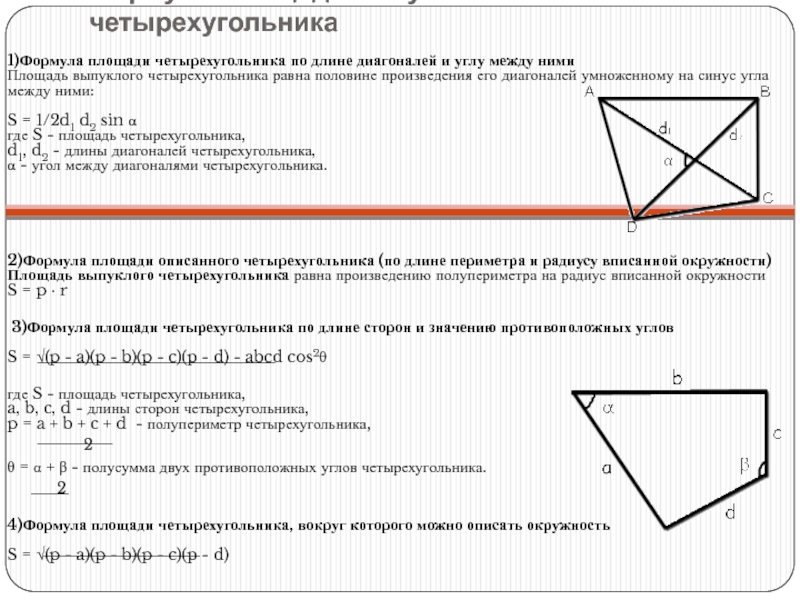
Слайд 19Формулы площади выпуклого четырехугольника
1)Формула площади четырехугольника по длине диагоналей и углу
2)Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности) Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности S = p · r
3)Формула площади четырехугольника по длине сторон и значению противоположных углов S = √(p - a)(p - b)(p - c)(p - d) - abcd cos2θ
где S - площадь четырехугольника, a, b, c, d - длины сторон четырехугольника, p = a + b + c + d - полупериметр четырехугольника,
2
θ = α + β - полусумма двух противоположных углов четырехугольника.
2
4)Формула площади четырехугольника, вокруг которого можно описать окружность S = √(p - a)(p - b)(p - c)(p - d)
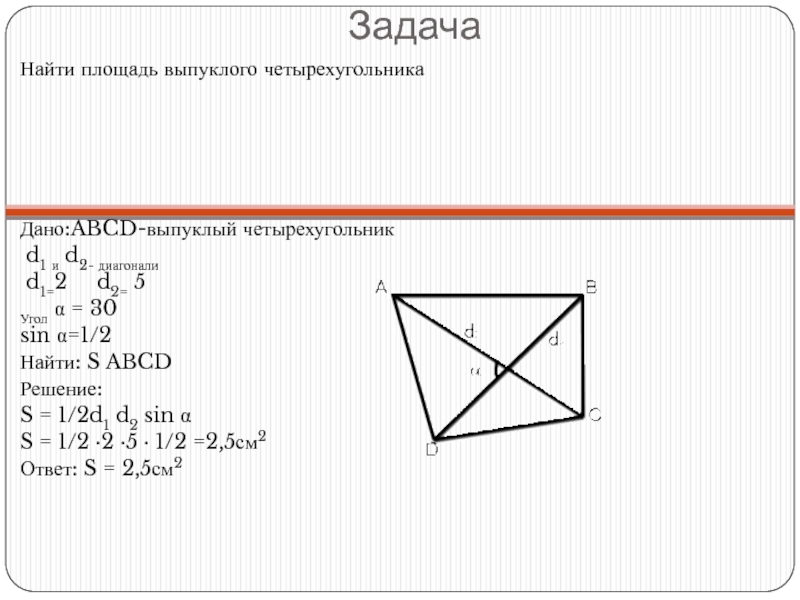
Слайд 20Задача
Найти площадь выпуклого четырехугольника
Дано:ABCD-выпуклый четырехугольник
d1 и d2- диагонали
d1=2
Угол α = 30
sin α=1/2
Найти: S ABCD
Решение:
S = 1/2d1 d2 sin α
S = 1/2 ∙2 ∙5 ∙ 1/2 =2,5см2
Ответ: S = 2,5см2
Слайд 21Формулы площади круга
1)Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса
2)Формула площади круга через диаметр Площадь круга равна четверти произведения квадрата диаметра на число пи.
S = 1π d2
4
где S - Площадь круга, r - длина радиуса круга, d - длина диаметра круга.
Слайд 22Задача
Найти площадь круга
Дано: Окр(О;r=2)
π =3.14
Найти:S окружности
Решение:
S = π r2
S =3.14 ∙ 22 =12.56 см2
Ответ:
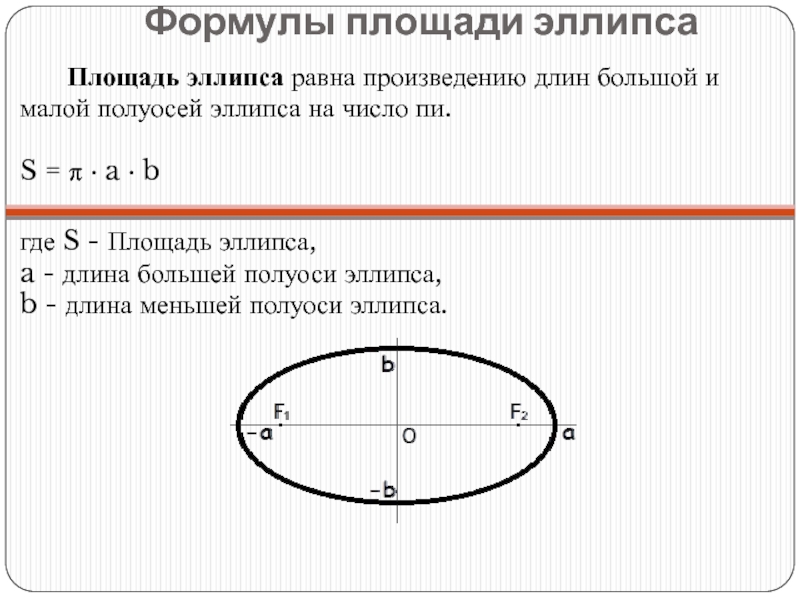
Слайд 23Формулы площади эллипса
Площадь эллипса равна произведению длин большой и малой полуосей
где S - Площадь эллипса, a - длина большей полуоси эллипса, b - длина меньшей полуоси эллипса.
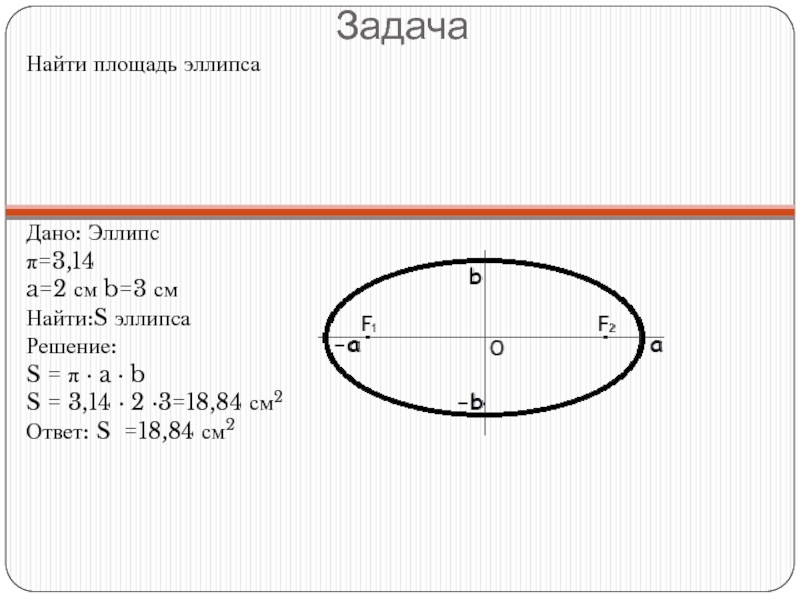
Слайд 24Задача
Найти площадь эллипса
Дано: Эллипс
π=3,14
a=2 см b=3 см
Найти:S эллипса
Решение:
S = π · a · b
S = 3,14 ·
Ответ: S =18,84 см2