- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Икосаэдр. Виды икосаэдров презентация
Содержание
- 1. Икосаэдр. Виды икосаэдров
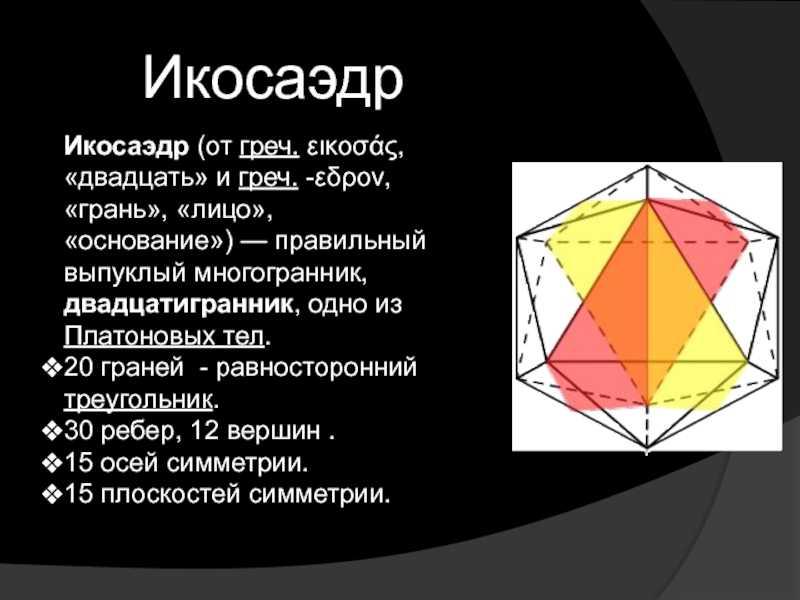
- 2. Икосаэдр Икосаэдр (от греч. εικοσάς, «двадцать» и
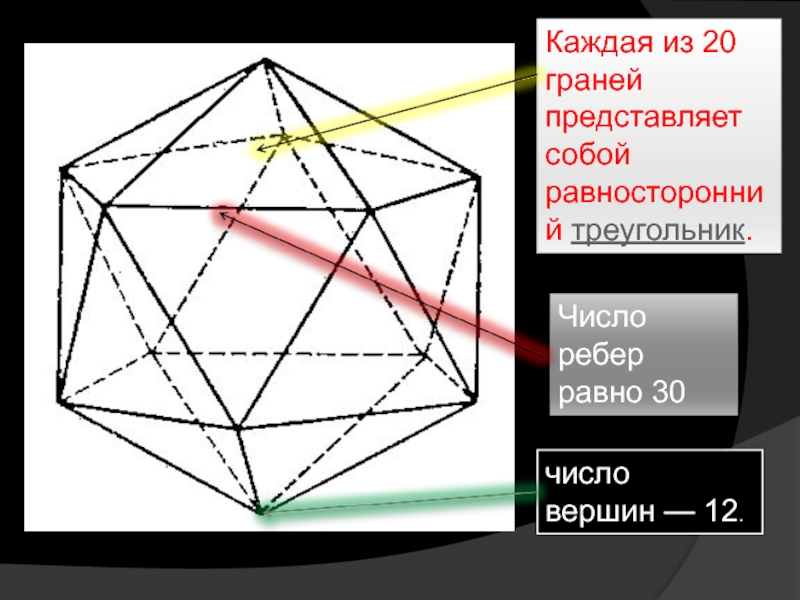
- 3. Каждая из 20 граней представляет собой равносторонний треугольник. Число ребер равно 30 число вершин — 12.
- 4. Различные виды икосаэдров ЗВЁЗДЧАТЫЙ
- 5. Различные виды икосаэдров ЗВЁЗДЧАТЫЙ
- 6. Применение икосадэра: Икосаэдр лучше всего из
- 7. Усеченный икосаэдр применяется как приблизительная модель сферы
- 8. Икосаэдр можно вписать в куб, при этом,
- 9. В икосаэдр может быть вписан тетраэдр, притом,
- 10. Икосаэдр можно вписать в додекаэдр, при том вершины икосаэдра будут совмещены с центрами граней додекаэдра.
- 11. В икосаэдр можно вписать додекаэдр, при том вершины додекаэдра будут совмещены с центрами граней икосаэдра.
Икосаэдр Икосаэдр (от греч. εικοσάς, «двадцать» и греч. -εδρον, «грань», «лицо», «основание») — правильный выпуклый многогранник, двадцатигранник, одно из Платоновых тел. 20 граней - равносторонний треугольник. 30 ребер, 12 вершин .
Слайд 2Икосаэдр
Икосаэдр (от греч. εικοσάς, «двадцать» и греч. -εδρον, «грань», «лицо», «основание») —
правильный выпуклый многогранник, двадцатигранник, одно из Платоновых тел.
20 граней - равносторонний треугольник.
30 ребер, 12 вершин .
15 осей симметрии.
15 плоскостей симметрии.
20 граней - равносторонний треугольник.
30 ребер, 12 вершин .
15 осей симметрии.
15 плоскостей симметрии.
Слайд 3Каждая из 20 граней представляет собой равносторонний треугольник.
Число ребер равно 30
число
вершин — 12.
Слайд 4Различные виды икосаэдров
ЗВЁЗДЧАТЫЙ
УСЕЧЁННЫЙ
Первая звёздчатая форма
Вторая звёздчатая форма
Шестая звёздчатая форма
20 треугольных пирамид
пятигранные пики, 10 тетраэдров
12 длинных пиков
Слайд 5Различные виды икосаэдров
ЗВЁЗДЧАТЫЙ
УСЕЧЁННЫЙ
Правильный выпуклый многогранник, полученный добавлением к исходной фигуре
множества отсеков, которые образуются при продолжении граней икосаэдра. Учёные: Брюкнер, Уиллер, Дюваль, Флэзер, Петри, Дж. Миллер, Кокстер.
Свойства:
Икосаэдр можно вписать в куб
В икосаэдр может быть вписан тетраэдр
Икосаэдр можно вписать в додекаэдр
Усечённый икосаэдр может быть получен срезанием 12 вершин с образованием граней в виде правильных пятиугольников
Слайд 6Применение икосадэра:
Икосаэдр лучше всего из всех правильных многогранников подходит для
триангуляции сферы методом рекурсивного разбиения. Поскольку он содержит наибольшее среди них количество граней, искажение получающихся треугольников по отношению к правильным минимально.
Слайд 7Усеченный икосаэдр применяется как приблизительная модель сферы в футбольном мячеУсеченный икосаэдр
применяется как приблизительная модель сферы в футбольном мяче, в химии его структуру повторяет простейший из фуллеренов
Слайд 8Икосаэдр можно вписать
в куб, при этом, шесть
Взаимно
перпендикулярных рёбер
икосаэдра будут
Расположены
соответственно на шести
гранях
куба, остальные 24
ребра внутри куба, все
двенадцать вершин
икосаэдра будут лежать
на шести гранях куба
ребра внутри куба, все
двенадцать вершин
икосаэдра будут лежать
на шести гранях куба
Свойства:
Слайд 9В икосаэдр может быть вписан тетраэдр, притом, четыре вершины тетраэдра будут
совмещены с четырьмя вершинами икосаэдра.
Слайд 10Икосаэдр можно вписать в додекаэдр, при том вершины икосаэдра будут совмещены
с центрами граней додекаэдра.
Слайд 11В икосаэдр можно вписать додекаэдр, при том вершины додекаэдра будут совмещены
с центрами граней икосаэдра.
