- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Площа бічної та повної поверхонь конуса презентация
Содержание
- 1. Площа бічної та повної поверхонь конуса
- 2. Назва цієї фігури пішла від
- 3. Конус серед нас
- 5. Конус – це тіло, отримане обертанням прямокутного
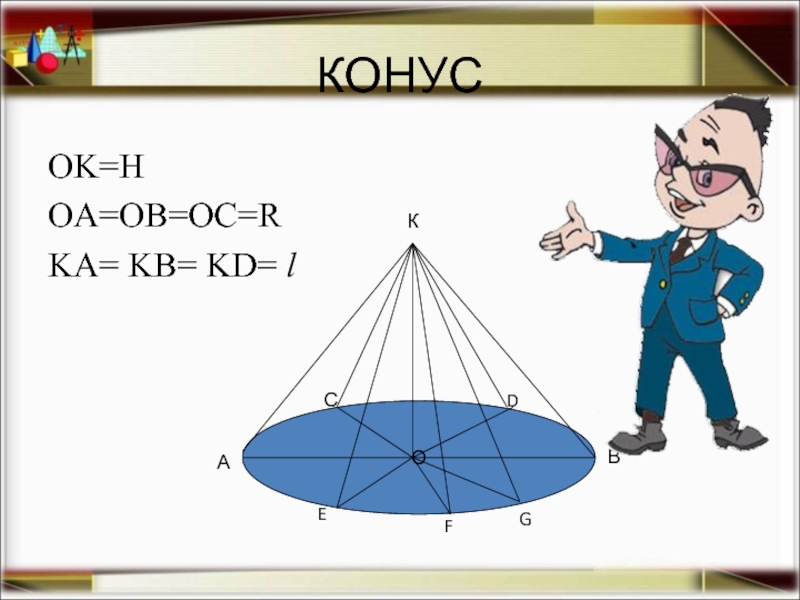
- 6. КОНУС OK=H OA=OB=OC=R KA= KB= KD= l
- 7. B P O R L Вісь
- 8. Розмітка БІЧНОЇ ПОВЕРХНІ КОНУСА – AK = r ПЛОЩА КРУГА: S = πr2
- 9. ФОРМУЛА ПЛОЩІ БІЧНОЇ ПОВЕРХНІ КОНУСА: Sб. =
- 10. ФОРМУЛА ПЛОЩІ ПОВНОЙ ПОВЕРХНІ КОНУСА Sп =
- 11. ЗАДАЧА 1 Дано: конус; R=3,l=5.
- 12. ЗАДАЧА 2. За даними малюнка
- 13. ЗАДАЧА 3. Дано: конус; R=5, h=12.
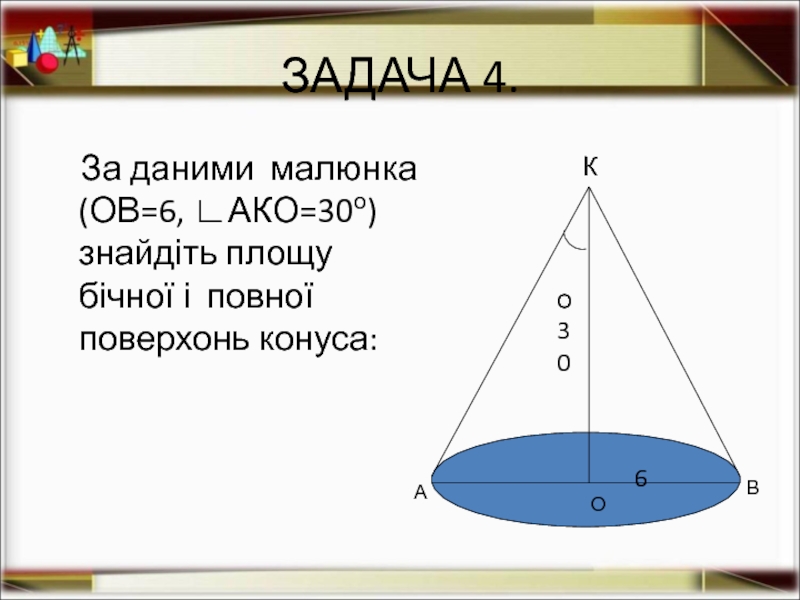
- 14. ЗАДАЧА 4. За даними малюнка
- 15. ЗАДАЧА 4. Дано: конус; R=6,∟АКО=30о. Знайти: SБ
- 16. Площа поверхні зрізаного конуса Площа бічної
- 17. Домашнє завдання: Зробити конспект лекції. Проаналізувати розв'язки
- 18. Задача № 1. Конусоподібну палатку висотою
- 19. Розв'язання задачі № 1 Нехай h
- 20. Розв'язання задачі № 2 Нехай h
- 21. ДЯКУЮ за урок!
Назва цієї фігури пішла від грецького слова «конос», так греки називали ялинкову шишку. Конус
Слайд 2 Назва цієї фігури пішла від грецького слова «конос», так
греки називали ялинкову шишку.
Конус
Слайд 5Конус – це тіло, отримане обертанням прямокутного трикутника навколо прямої, яка
є нерухомим катетом.
Це є одна з фігур обертання
Слайд 7
B
P
O
R
L
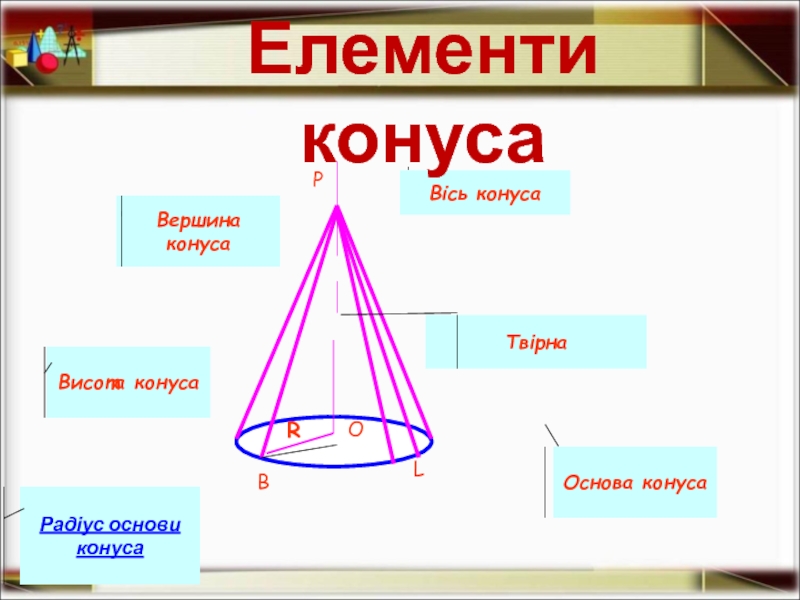
Вісь конуса
Вершина конуса
Твірна
Основа конуса
Висота конуса
Радіус основи конуса
Елементи конуса
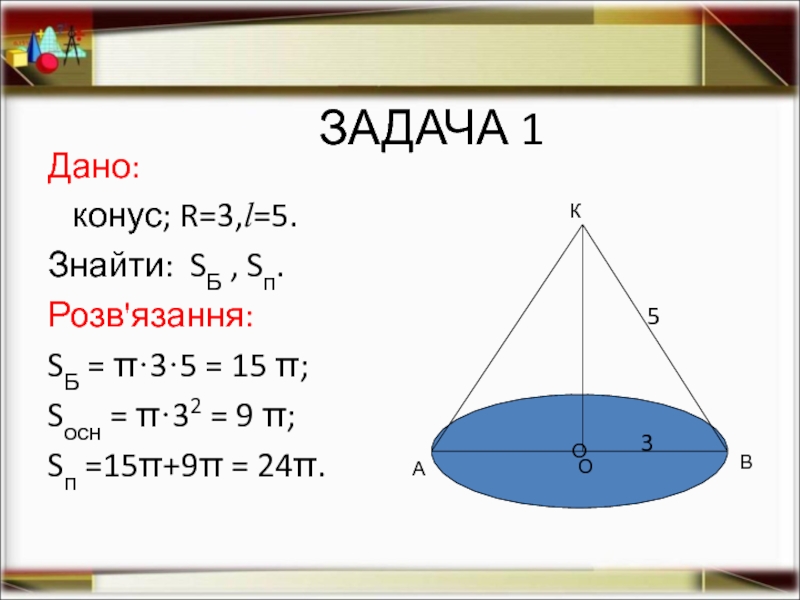
Слайд 11ЗАДАЧА 1
Дано:
конус; R=3,l=5.
Знайти: SБ , Sп.
Розв'язання:
SБ = π·3·5 =
15 π;
Sосн = π·32 = 9 π;
Sп =15π+9π = 24π.
Sосн = π·32 = 9 π;
Sп =15π+9π = 24π.
О
А
В
К
3
5
О
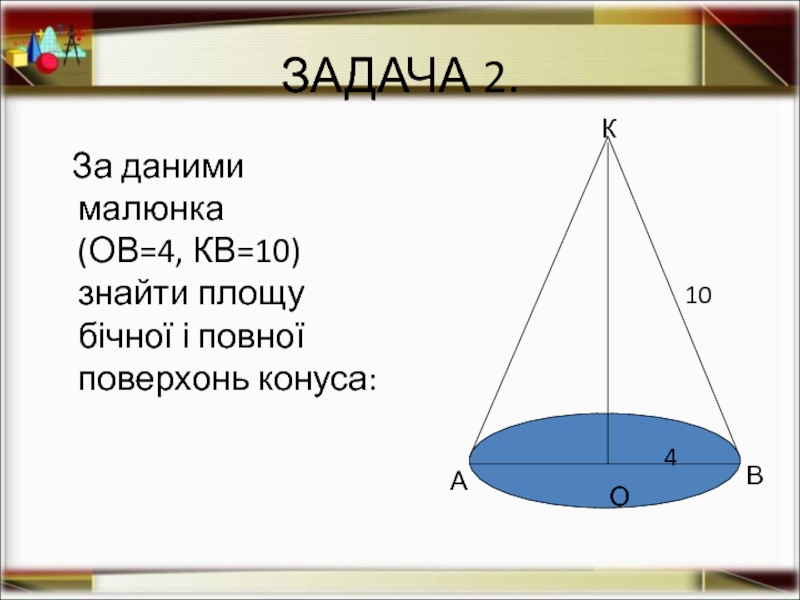
Слайд 12ЗАДАЧА 2.
За даними малюнка (ОВ=4, КВ=10)
знайти площу бічної і повної поверхонь конуса:
А
О
В
К
4
10
Слайд 13ЗАДАЧА 3.
Дано: конус; R=5, h=12.
Знайти: SБ , Sп.
Розв'язання:
l2=144+25=169,
l =13;
SБ=π·13·5=65 π;
Sосн = π·52 =25 π;
Sп = 65π+25π; Sп = 90π.
SБ=π·13·5=65 π;
Sосн = π·52 =25 π;
Sп = 65π+25π; Sп = 90π.
О
В
К
5
12
А
Слайд 14ЗАДАЧА 4.
За даними малюнка (ОВ=6, ∟АКО=30о)
знайдіть площу бічної і повної поверхонь конуса:
о
30
К
А
В
О
6
Слайд 15ЗАДАЧА 4.
Дано: конус; R=6,∟АКО=30о.
Знайти: SБ , Sп.
Розв'язання:
l = R/sin30о,l=6/0.5=12;
SБ= π·12·6=72π;
Sосн =
π·62 =36π;
Sп = 72π+36π;
Sп = 108π.
Sп = 72π+36π;
Sп = 108π.
о
30
К
А
В
О
6
Слайд 16Площа поверхні зрізаного конуса
Площа бічної поверхні зрізаного конуса дорівнює добутку півсуми
довжин кіл основ на твірну конуса:
Sбіч = π(r + R)l.
площа повної поверхні зрізаного конуса.
Sзр.к = Sбіч + πr2 + πR2
Sзр.к =π(r + R)l + πr2 + πR2
Sбіч = π(r + R)l.
площа повної поверхні зрізаного конуса.
Sзр.к = Sбіч + πr2 + πR2
Sзр.к =π(r + R)l + πr2 + πR2
Слайд 17Домашнє завдання:
Зробити конспект лекції.
Проаналізувати розв'язки задач і заповнити пропуски у їх
розв'язанні.
Виконати індивідуальні завдання (10 варіантів)
Виконати індивідуальні завдання (10 варіантів)
Слайд 18
Задача № 1. Конусоподібну палатку висотою 3,5 м і діаметром основи
4 м покрито тканиною. Скільки квадратних метрів тканини пішло на палатку?
Задача № 2. Дах силосної башти має форму конуса. Висота доху 2 м, а діаметр башти 6 м. Знайти поверхню даху.
Задача № 2. Дах силосної башти має форму конуса. Висота доху 2 м, а діаметр башти 6 м. Знайти поверхню даху.
Слайд 19Розв'язання задачі № 1
Нехай h = 3,5 м і D =
... м,
тоді S = πrl, де r — радіус основи конуса;
r=………. =2 (м);
l — твірна конуса; l=…………………………………………………(м).
S = π ·2 · ... 25,3 (м2).
Відповідь. 25,3 м2.
тоді S = πrl, де r — радіус основи конуса;
r=………. =2 (м);
l — твірна конуса; l=…………………………………………………(м).
S = π ·2 · ... 25,3 (м2).
Відповідь. 25,3 м2.
Слайд 20Розв'язання задачі № 2
Нехай h = ... і D = 6
м,
тоді S = πrl, де r — радіус основи конуса;
r = …………………… (м);
l — твірна конуса;
l = ……………………………………………………………(м).
S = 3,14 · 3 · 3,6 = ... (м2).
Відповідь. 33,98 м2.
тоді S = πrl, де r — радіус основи конуса;
r = …………………… (м);
l — твірна конуса;
l = ……………………………………………………………(м).
S = 3,14 · 3 · 3,6 = ... (м2).
Відповідь. 33,98 м2.
