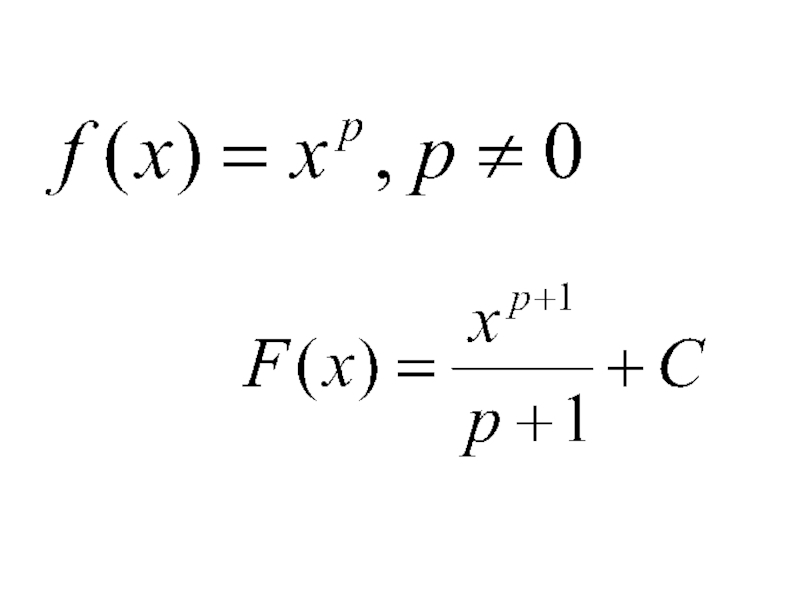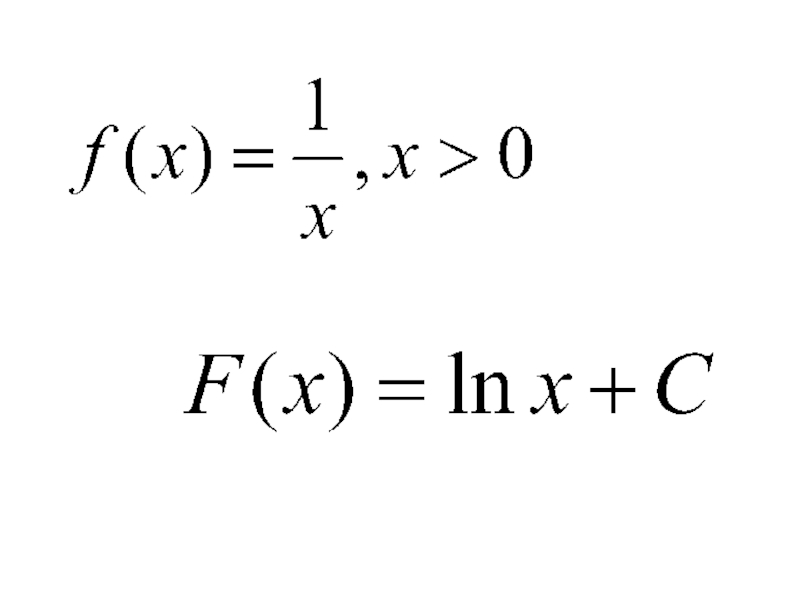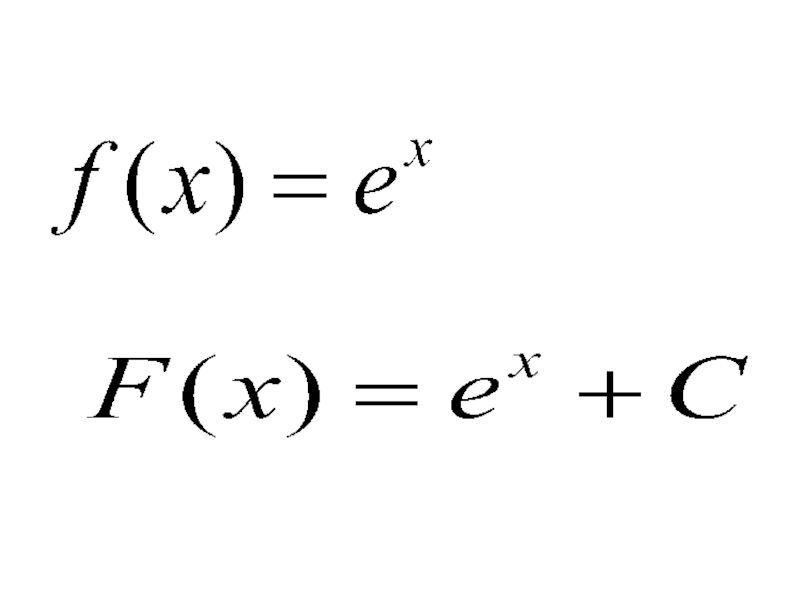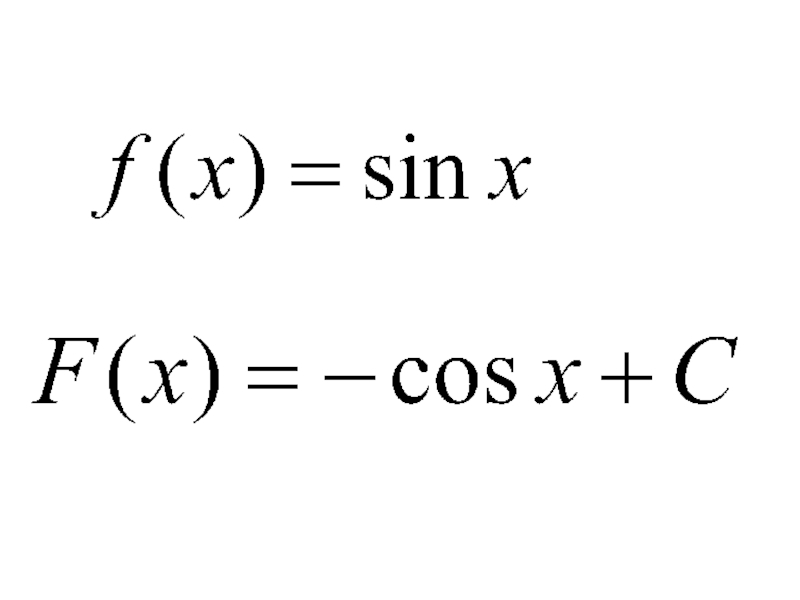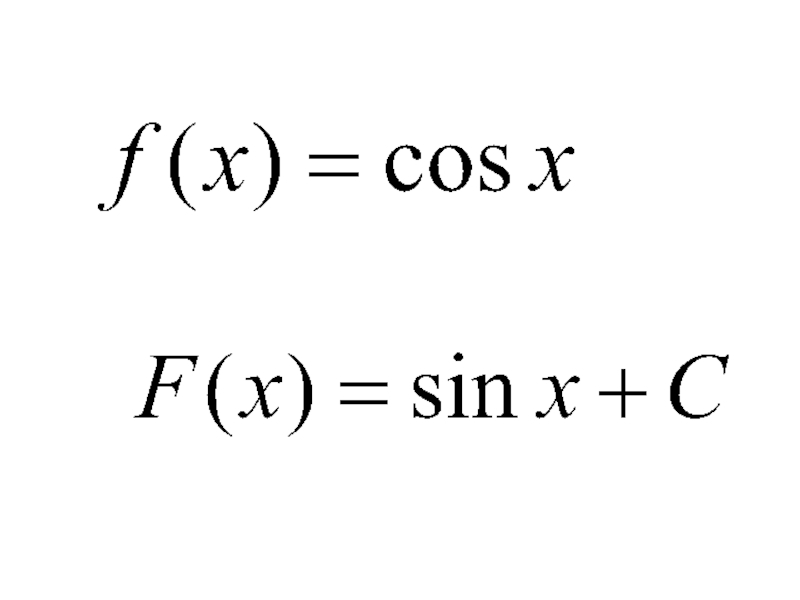Первообразная. Правила нахождения первообразных презентация

Содержание

1. Первообразная. Правила нахождения первообразных
2. Функция F(x)называется первообразной для функции f(x)на некотором
3. Показать, что функция является первообразной для функции Решение:
4. Показать, что функция является первообразной для функции Решение:
5. Если F(x)– первообразная для функции f(x) на
11. Правила нахождения первообразных
12. Если F(x)– первообразная для функции f(x), а
13. Если F(x)– первообразная для функции f(x), а
14. Если F(x) – первообразная для функции f(x),
15. Найти первообразные для функции Решение:

Функция F(x)называется первообразной для функции f(x)на некотором промежутке, если для всех x из этого промежутка

Главная
Математика
Первообразная. Правила нахождения первообразных

Слайд 1Первообразная
Правила нахождения первообразных

Слайд 2Функция F(x)называется первообразной для функции f(x)на некотором промежутке, если для всех

x из этого промежутка

Слайд 3Показать, что функция
является первообразной для функции
Решение:

Слайд 4Показать, что функция
является первообразной для функции
Решение:

Слайд 5Если F(x)– первообразная для функции f(x) на некотором промежутке, то функция

F(x)+C также является первообразной функции f(x) на этом промежутке, где C –произвольная постоянная.

Слайд 6

Слайд 7

Слайд 8

Слайд 9

Слайд 10

Слайд 11Правила нахождения первообразных

Слайд 12Если F(x)– первообразная для функции f(x), а G(x)– первообразная для функции

g(x), то F(x)+G(x)– первообразная для функции f(x)+g(x)

Первообразная суммы равна сумме первообразных

Слайд 13Если F(x)– первообразная для функции f(x), а а –константа, то аF(x)–

первообразная для функции аf(x)

Постоянный множитель можно выносить за знак первообразной

Слайд 14Если F(x) – первообразная для функции f(x), а k и b-

константы, причем

то

-первообразная для функции

Слайд 15Найти первообразные для функции
Решение:

Скачать презентацию

Первообразная. Правила нахождения первообразных презентация

Содержание

Слайд 1Первообразная
Правила нахождения первообразных

Слайд 2Функция F(x)называется первообразной для функции f(x)на некотором промежутке, если для всех

Слайд 3Показать, что функция
является первообразной для функции
Решение:

Слайд 4Показать, что функция
является первообразной для функции
Решение:

Слайд 5Если F(x)– первообразная для функции f(x) на некотором промежутке, то функция

Слайд 6

Слайд 7

Слайд 8

Слайд 9

Слайд 10

Слайд 11Правила нахождения первообразных

Слайд 12Если F(x)– первообразная для функции f(x), а G(x)– первообразная для функции

Слайд 13Если F(x)– первообразная для функции f(x), а а –константа, то аF(x)–

Слайд 14Если F(x) – первообразная для функции f(x), а k и b-

Слайд 15Найти первообразные для функции
Решение:

Обратная связь

Что такое ThePresentation.ru?

Первообразная. Правила нахождения первообразных презентация

Содержание

Слайд 1Первообразная Правила нахождения первообразных

Слайд 2Функция F(x)называется первообразной для функции f(x)на некотором промежутке, если для всех

Слайд 3Показать, что функция является первообразной для функции Решение:

Слайд 4Показать, что функция является первообразной для функции Решение:

Слайд 5Если F(x)– первообразная для функции f(x) на некотором промежутке, то функция

Слайд 6

Слайд 7

Слайд 8

Слайд 9

Слайд 10

Слайд 11Правила нахождения первообразных

Слайд 12Если F(x)– первообразная для функции f(x), а G(x)– первообразная для функции

Слайд 13Если F(x)– первообразная для функции f(x), а а –константа, то аF(x)–

Слайд 14Если F(x) – первообразная для функции f(x), а k и b-

Слайд 15Найти первообразные для функцииРешение:

Похожие презентации

Обратная связь

Что такое ThePresentation.ru?

Слайд 1Первообразная
Правила нахождения первообразных

Слайд 3Показать, что функция
является первообразной для функции
Решение:

Слайд 4Показать, что функция
является первообразной для функции
Решение:

Слайд 15Найти первообразные для функции
Решение: