- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Гармонический анализ презентация
Содержание
- 1. Гармонический анализ
- 2. 15. 1. ОСНОВЫ ГАРМОНИЧЕСКОГО АНАЛИЗА Функция
- 3. Если Т – период функции, то при
- 4. 1
- 5. Где Аn и αn – постоянные величины,
- 6. Проверим это для одной из функций: Если
- 7. Поставим обратную задачу: можно ли данную периодическую
- 8. Ряд вида называется тригонометрическим рядом.
- 9. Числа an и bn –называются коэффициентами этого
- 10. Следовательно, любая частичная сумма тригонометрического ряда тоже
Слайд 215. 1. ОСНОВЫ ГАРМОНИЧЕСКОГО
АНАЛИЗА
Функция f(x) называется периодической на
промежутке Х, если
наименьшее число Т, называемое периодом
функции, что для любого х выполняется
равенство
f(x+T)=f(x)
Слайд 3Если Т – период функции, то при
где n – целое
Поэтому число nТ тоже часто называют периодом функции в широком понимании этого слова.
Простейшими периодическими функциями являются sin x и cоs x с периодом 2П.
Из простых периодических функций можно составить более сложные.
Например, рассмотрим функции
Слайд 5Где Аn и αn – постоянные величины, которые называются амплитудой и
Периоды для этих функций равны:
Слайд 6Проверим это для одной из функций:
Если сложить эти функции, то снова
Слайд 7Поставим обратную задачу: можно ли данную периодическую функцию f(x) с периодом
Такая задача решается для широкого класса функций и называется гармоническим анализом.
При этом отдельные функции вида (1) называются гармоническими составляющими или гармониками функции f(x).
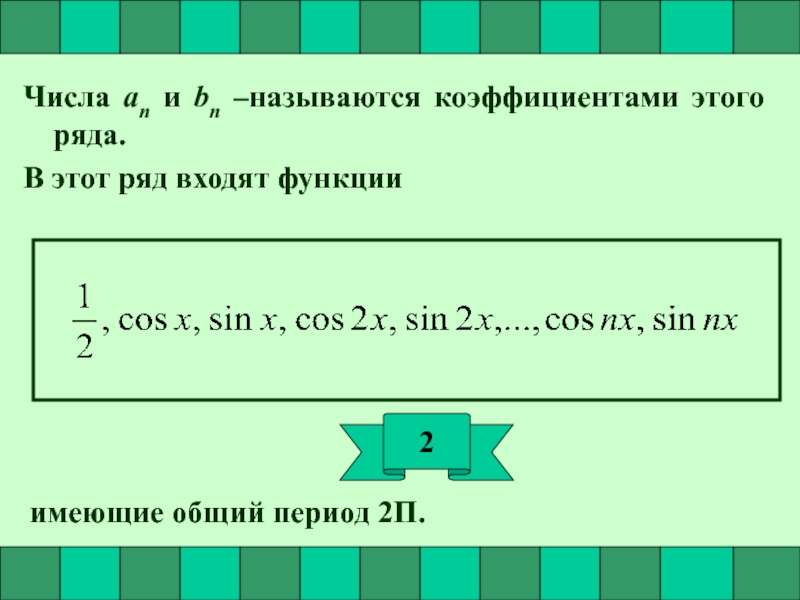
Слайд 9Числа an и bn –называются коэффициентами этого ряда.
В этот ряд входят
имеющие общий период 2П.
2
Слайд 10Следовательно, любая частичная сумма тригонометрического ряда тоже будет периодической функцией с
Поэтому, если ряд сходится на отрезке [-П,П], то он сходится и на всей числовой прямой.