- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вычисление объемов пространственных тел с помощью интеграла презентация
Содержание
- 1. Вычисление объемов пространственных тел с помощью интеграла
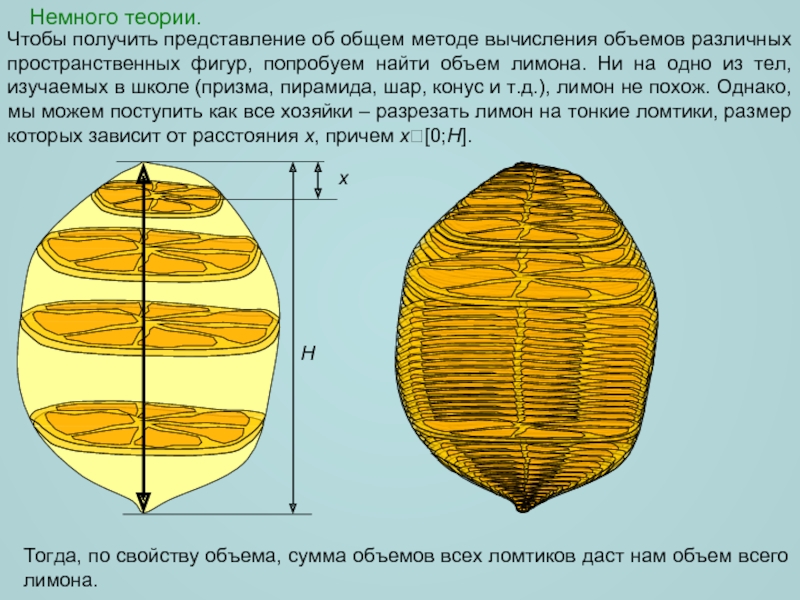
- 2. Немного теории. Чтобы получить представление об
- 3. Немного теории. H x x С
- 4. Немного теории (базовые классы могут пропустить).
- 5. I. Объем прямоугольного параллелепипеда с
- 6. II. Объем прямой призмы с высотой
- 7. III. Объем n-угольной прямой призмы
- 8. IV. Объем наклонной призмы с высотой
- 9. V. Объем треугольной пирамиды с высотой H
- 10. VI. Объем n-угольной пирамиды с высотой
- 11. VII. Объем усеченной пирамиды. текст
- 12. VIII. Объем цилиндра с высотой H
- 13. IX. Объем конуса с высотой H
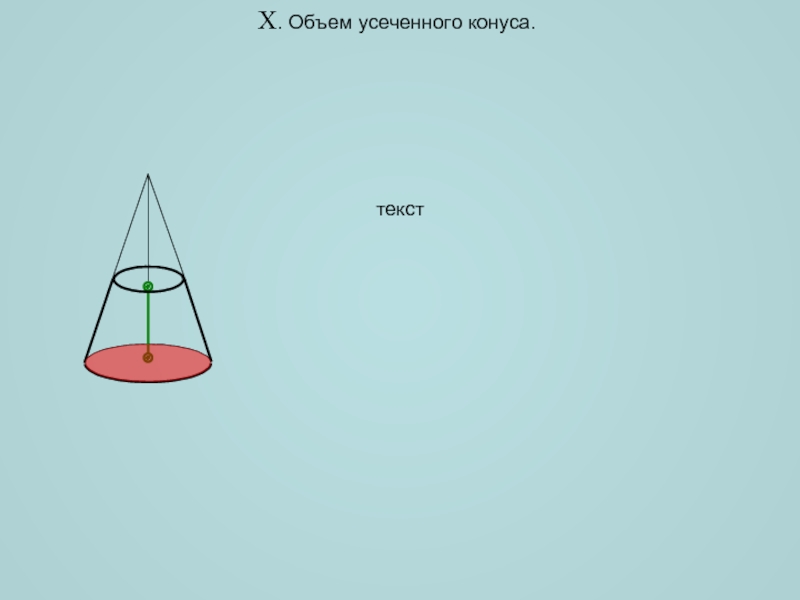
- 14. X. Объем усеченного конуса. текст
- 15. XI. Объем шара с радиусом R. Найдем
- 16. XII. Объем шарового сегмента.
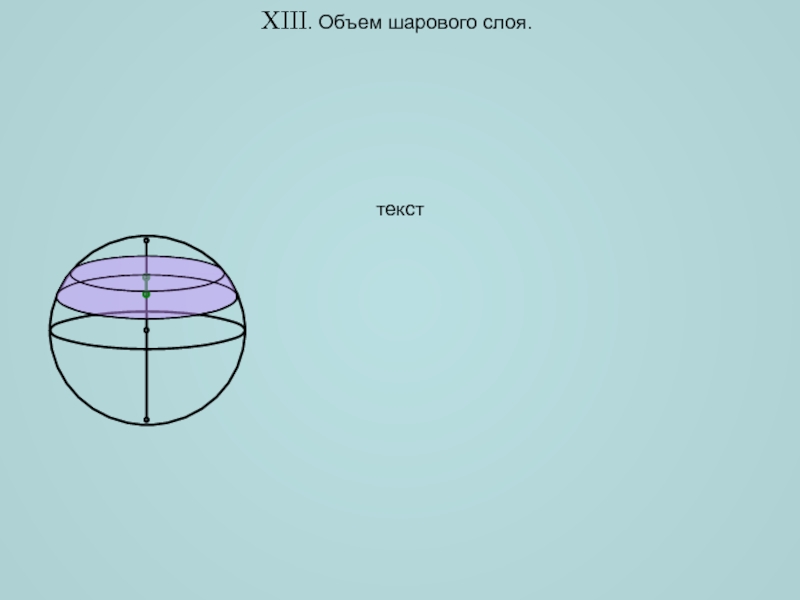
- 17. XIII. Объем шарового слоя. текст
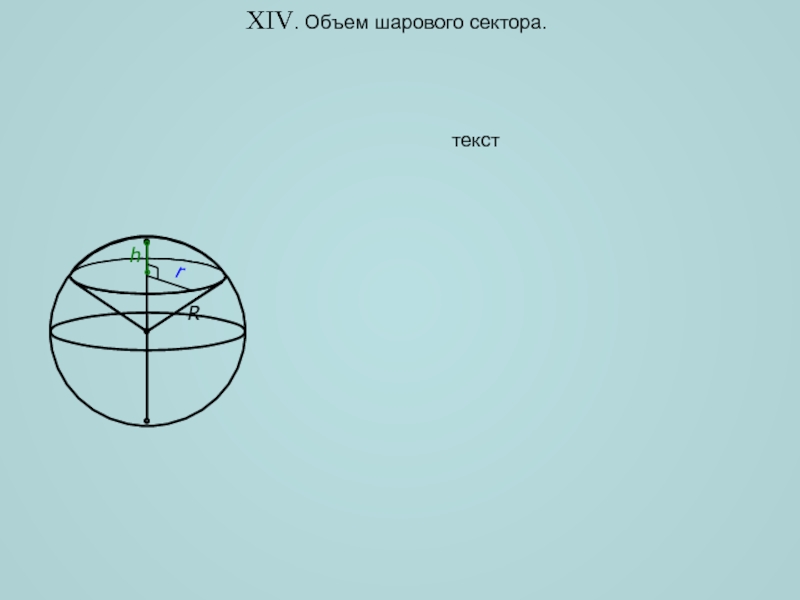
- 18. XIV. Объем шарового сектора. текст
Слайд 1Вычисление объемов пространственных тел с помощью интеграла.
Воробьев Леонид Альбертович, г.Минск
Слайд 2
Немного теории.
Чтобы получить представление об общем методе вычисления объемов различных пространственных
H
x
Тогда, по свойству объема, сумма объемов всех ломтиков даст нам объем всего лимона.
Слайд 3
Немного теории.
H
x
x
С точки зрения геометрии мы построили сечения пространственной фигуры плоскостями,
Проще говоря, при бесконечном числе разбиений каждый ломтик «вырождается» в плоское сечение и объем лимона равен бесконечной интегральной сумме площадей таких сечений, зависящих от расстояния x, т.е.
где H – высота тела, а Sсеч. – некоторая функция, зависящая от x, причем x[0;H].
Sсеч.
Слайд 4
Немного теории (базовые классы могут пропустить).
H
x
x
Если принять число разбиений бесконечно большим
где H – высота тела, а Sсеч. – некоторая функция, зависящая от x, причем x[0;H].
Sсеч.
Слайд 5
I. Объем прямоугольного параллелепипеда
с высотой H и площадью основания S.
x
H
x[0;H]
0
Площадь сечения
x
Слайд 6
II. Объем прямой призмы
с высотой H и площадью основания S.
x
x[0;H]
H
0
Площадь сечения
x
Слайд 7
III. Объем n-угольной прямой призмы
с высотой H и площадью основания
x
x[0;H]
H
0
Площадь сечения не изменяется в любой точке отрезка от 0 до H и равна площади основания.
x
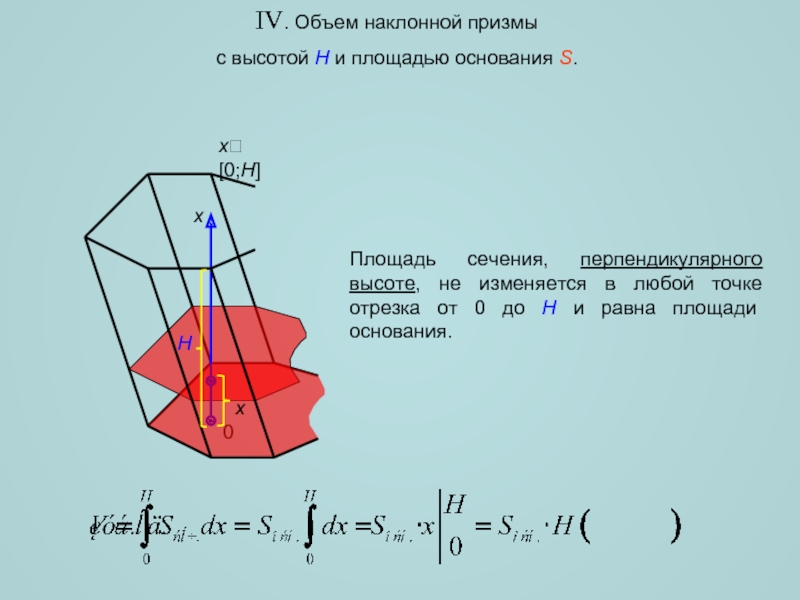
Слайд 8IV. Объем наклонной призмы
с высотой H и площадью основания S.
Площадь
x
H
x[0;H]
0
x
Слайд 9V. Объем треугольной пирамиды
с высотой H и площадью основания S.
H
x
x[0;H]
⇒
x
Площадь сечения
0
Слайд 10
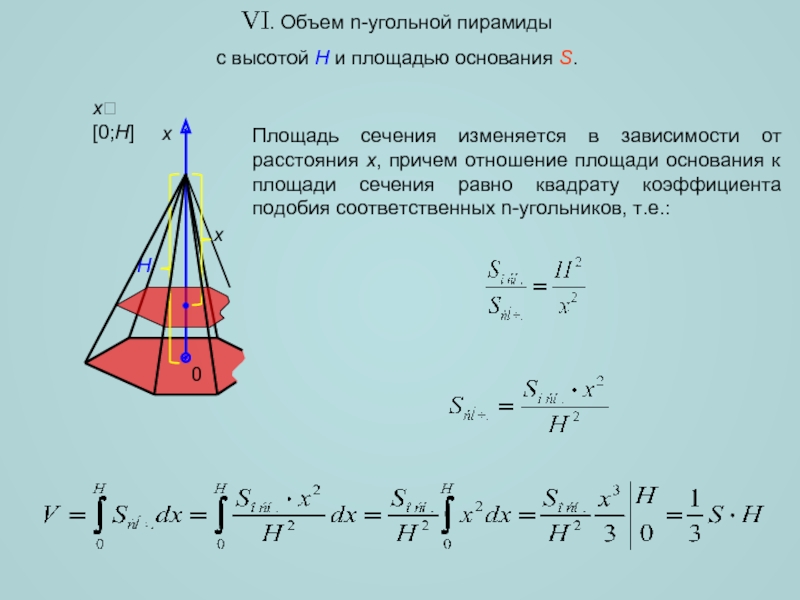
VI. Объем n-угольной пирамиды
с высотой H и площадью основания S.
H
x
Площадь сечения
x
x[0;H]
0
Слайд 12
VIII. Объем цилиндра с высотой H и площадью основания S.
x
x[0;H]
H
0
x
Площадь сечения
Слайд 13
IX. Объем конуса с высотой H и площадью основания S.
x
x[0;H]
H
x
Площадь сечения
0
Слайд 15XI. Объем шара с радиусом R.
Найдем объем полушария, как бесконечную интегральную
R
x
Значит, объем всего шара равен:
x
0
r
Слайд 16XII. Объем шарового сегмента.
Вывод объема шарового сегмента с высотой h и
r
R
h
x
Обратите внимание, что в формуле объема шарового сегмента участвует радиус шара (R), а не радиус основания сегмента (r)!



![I. Объем прямоугольного параллелепипедас высотой H и площадью основания S.xHx[0;H]0Площадь сечения не изменяется в любой](/img/tmb/2/135261/d4d7816c161ea91120d327cf1887e206-800x.jpg)
![II. Объем прямой призмыс высотой H и площадью основания S.xx[0;H]H0Площадь сечения не изменяется в любой](/img/tmb/2/135261/fc83b7f10985127af12bab877914b7c5-800x.jpg)
![III. Объем n-угольной прямой призмы с высотой H и площадью основания S.xx[0;H]H0Площадь сечения не изменяется](/img/tmb/2/135261/808704d5714f747df7bd979da0913ec7-800x.jpg)
![V. Объем треугольной пирамидыс высотой H и площадью основания S.Hxx[0;H]⇒xПлощадь сечения изменяется в зависимости от](/img/tmb/2/135261/4e3c2718807330b4cb163fae071ad7ad-800x.jpg)

![VIII. Объем цилиндра с высотой H и площадью основания S.xx[0;H]H0xПлощадь сечения не изменяется в любой](/img/tmb/2/135261/e55a136cbc5255f377531518c9a96f2e-800x.jpg)
![IX. Объем конуса с высотой H и площадью основания S.xx[0;H]HxПлощадь сечения изменяется в зависимости от](/img/tmb/2/135261/58d292af03dad1bc9ca85530481dec84-800x.jpg)