А.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Особые приёмы решения логарифмических неравенств с переменной в основании презентация
Содержание
- 1. Особые приёмы решения логарифмических неравенств с переменной в основании
- 2. Решение простейших логарифмических неравенств: a >
- 3. В предыдущем занятии было доказано: выражения log
- 4. Решение логарифмических неравенств с применением доказанного свойства:
- 5. Алгоритм решения неравенства log
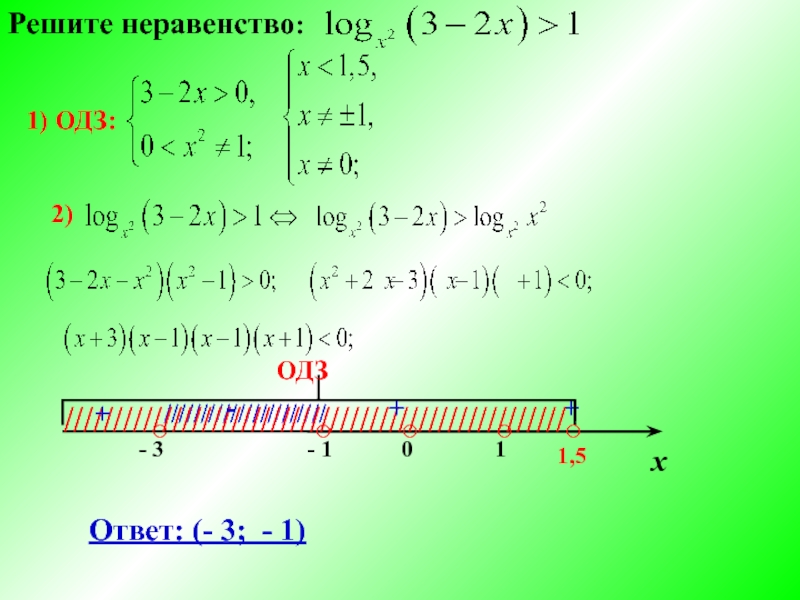
- 6. Решите неравенство: 1)
- 7. Решите неравенство:
- 8. Решите неравенство:
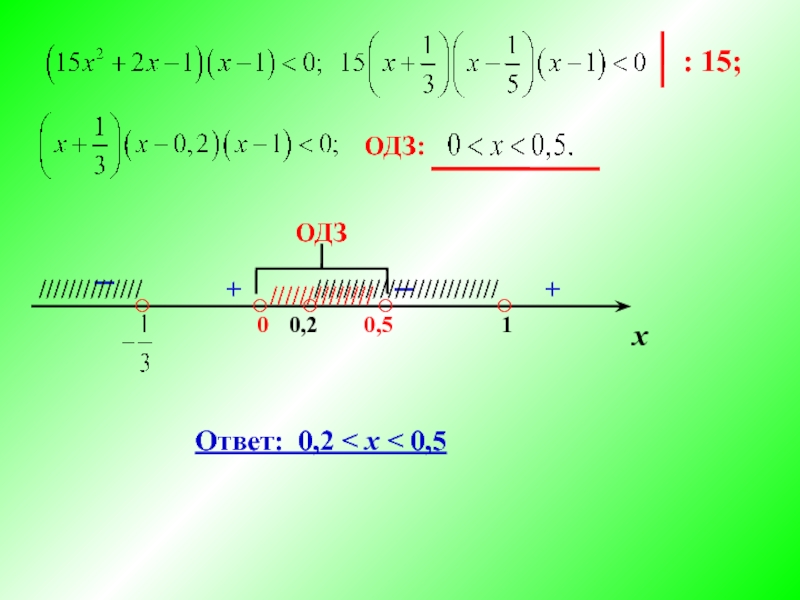
- 9. Решите неравенство: 1) ОДЗ: 2) ∙ ( - 1); ∙ ( - 15);
- 10. : 15; х 0,2 1 ○ ○
- 11. 1) Решите неравенство: Ответ: 2) Решите неравенство: Ответ:
- 12. Продолжение следует, до новых встреч
Решение простейших логарифмических неравенств: a > 1 x1 > x2 > 0 a > 1 x2 > x1 > 0 0 < a < 1 x2 > x1
Слайд 1Особые приёмы решения
логарифмических
неравенств с переменной
в основании
Занятие №2
Методическая разработка
учителя Поляковой Е.
Слайд 2
Решение простейших логарифмических неравенств:
a > 1
x1 > x2 > 0
a >
1
x2 > x1 > 0
x2 > x1 > 0
0 < a < 1
x2 > x1 > 0
0 < a < 1
x1 > x2 > 0
Слайд 5
Алгоритм решения неравенства log h(x) f(x) > log h(x) g(x)
1)
Находим область допустимых значений переменной (ОДЗ):
2) Решаем неравенство (f(х) – g(х))(h(х) – 1) > 0.
(Условимся далее две последние строки системы писать одной так: 0 < h(x) ≠ 1)
3) Для найденного решения учитываем ОДЗ.
4) Записываем ответ.
Слайд 6
Решите неравенство:
1) ОДЗ:
2) Переписываем неравенство в виде
Решаем неравенство (х – 1
– (х – 3) 2)(х – 3 – 1) < 0;
(х – 1 – х 2 + 6 x – 9)(х – 4) < 0;
–( х 2 – 7 x + 10)(х – 4) < 0;
(х – 5)(х – 2)(х – 4) > 0;
х
○
○
3
5
+
–
+
/////////////////////////////////
2
○
/////////////////////////////////////////
ОДЗ
( х 2 – 7 x + 10)(х – 4) > 0;
○
4
–
//////////////////
Ответ: 3 < x < 4; x > 5
Слайд 7
Решите неравенство:
1) ОДЗ:
○
- 3
- 1
1
х
+
2)
//////////////////////
1,5
///////////////////////////////////////////////////
ОДЗ
○
○
+
-
+
0
○
○
Ответ: (- 3; - 1)
Слайд 8
Решите неравенство:
1) ОДЗ:
○
- 3
1
х
+
2)
○
○
-
+
○
-
+
///////////
///////////////////////
//////////////////
0
○
///////////////////////////
ОДЗ
Ответ:
Слайд 10: 15;
х
0,2
1
○
○
○
+
─
+
─
//////////////
/////////////////////////
ОДЗ:
0
○
0,5
○
//////////////
ОДЗ
Ответ: 0,2 < x < 0,5
