- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы теории случайных процессов презентация
Содержание
- 1. Основы теории случайных процессов
- 2. Пространство элементарных событий (генеральная совокупность) Основные понятия
- 3. Основные понятия теории вероятностей
- 4. Случайная величина
- 5. Случайная величина
- 8. Примеры ФР и ПРВ
- 9. Числовые характеристики с.в.
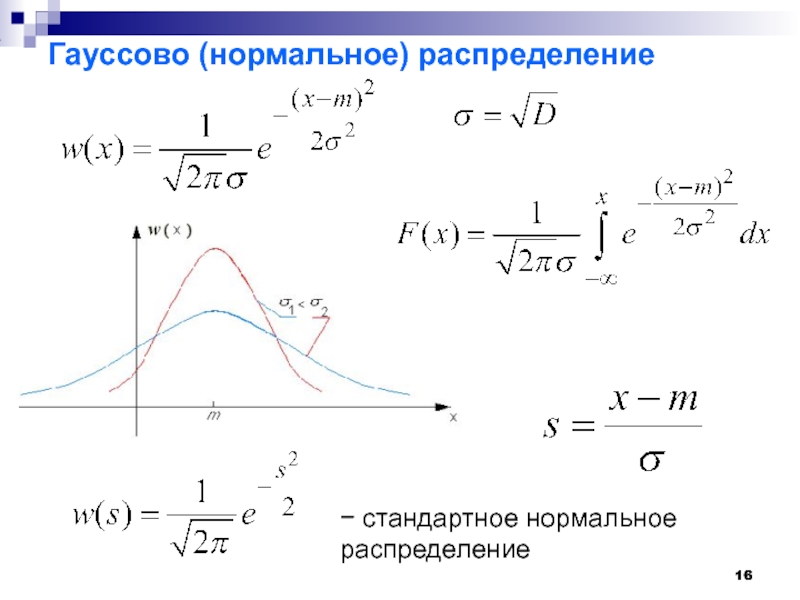
- 16. Гауссово (нормальное) распределение
- 17. Стандартное гауссово распределение
- 18. Стандартное гауссово распределение
- 20. Числовые характеристики с.в.
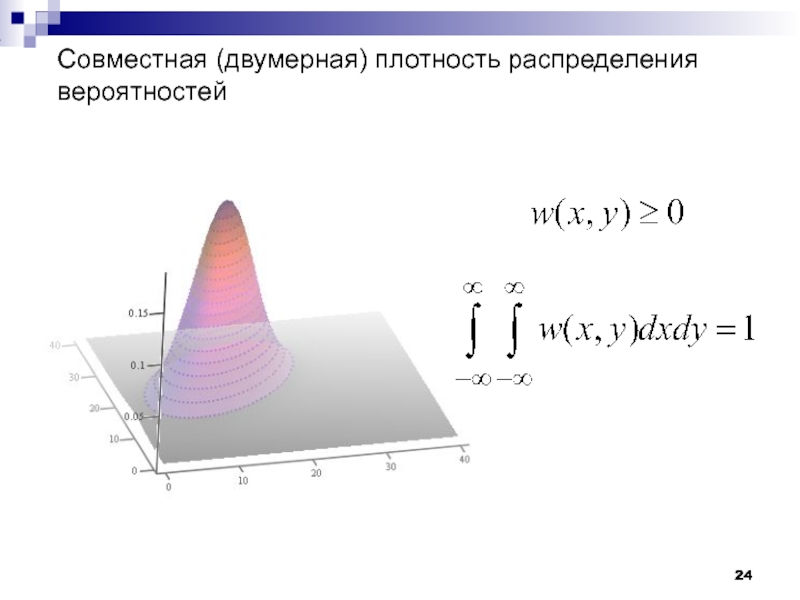
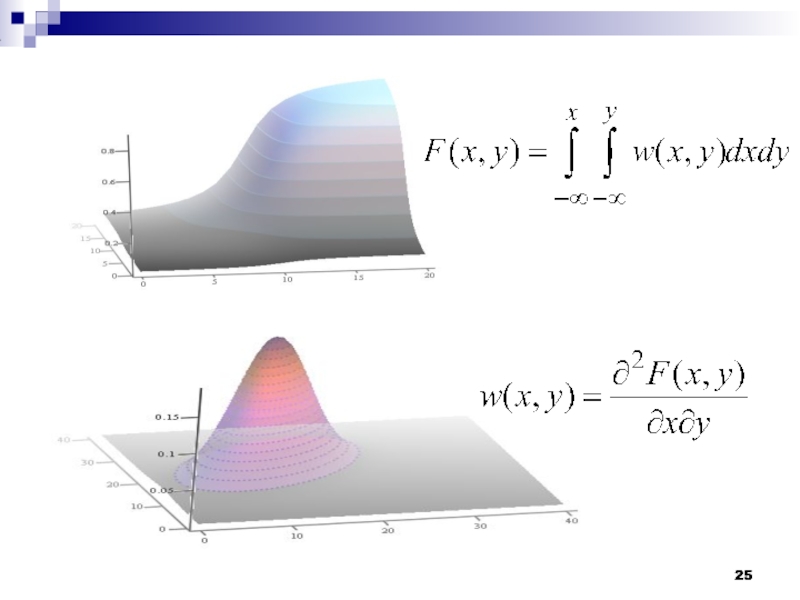
- 21. Системы случайных величин
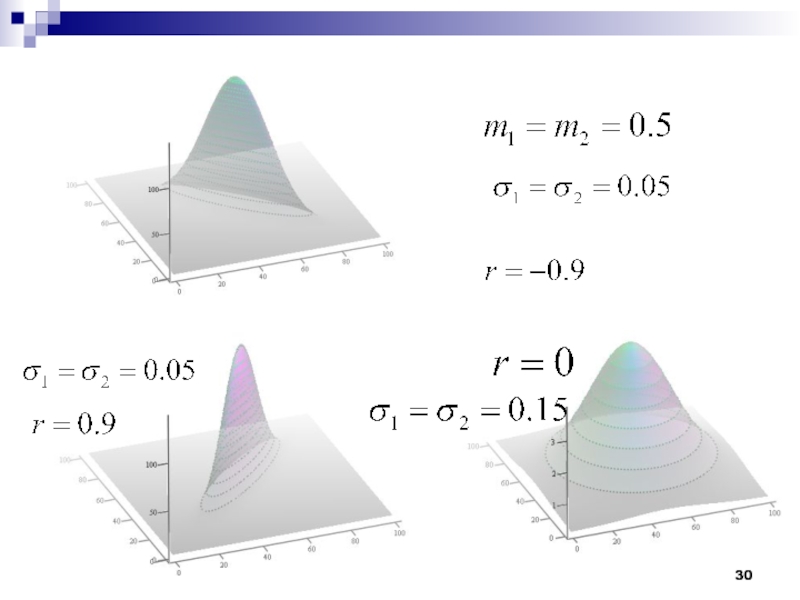
- 26. Числовые характеристики системы 2 случайных величин
- 28. Пример. Пара гауссовских случайных величин
Пространство элементарных событий (генеральная совокупность) Основные понятия теории вероятностей Все сигналы
Слайд 2Пространство элементарных событий (генеральная совокупность)
Основные понятия теории вероятностей
Все сигналы и все
помехи являются случайными, то есть непредсказуемыми.
Математическими моделями случайных сигналов и помех служат случайные процессы.
Математическими моделями случайных сигналов и помех служат случайные процессы.
В основе лежит понятие случайного события
− случайное событие
элементарное событие
Слайд 3Основные понятия теории вероятностей
− случайное событие
− элементарное случайное событие
− вероятностная мера
(функция множеств)
− вероятность случайного события
достоверное событие
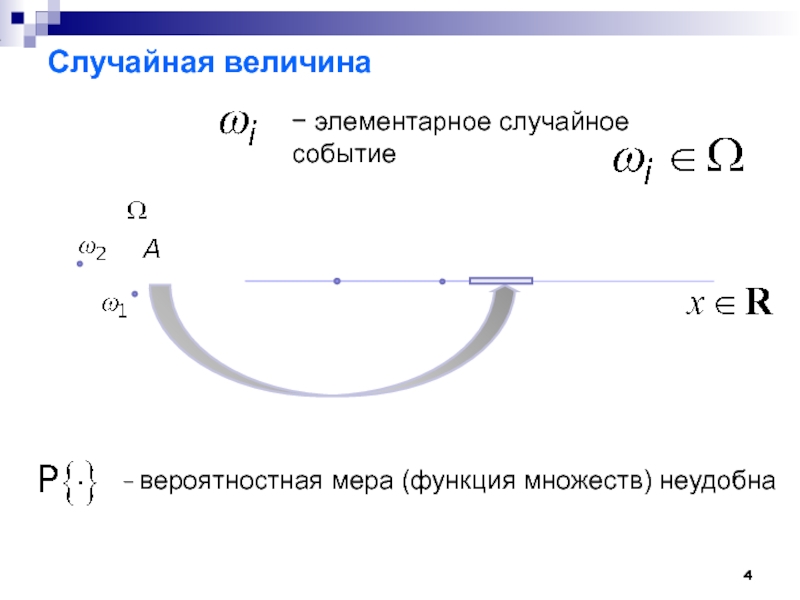
Слайд 4
Случайная величина
− элементарное случайное событие
− вероятностная мера (функция множеств) неудобна
Слайд 5Случайная величина
− вероятностная мера (функция множеств) неудобна
− функция распределения с.в.
функция распределения
не убывает !
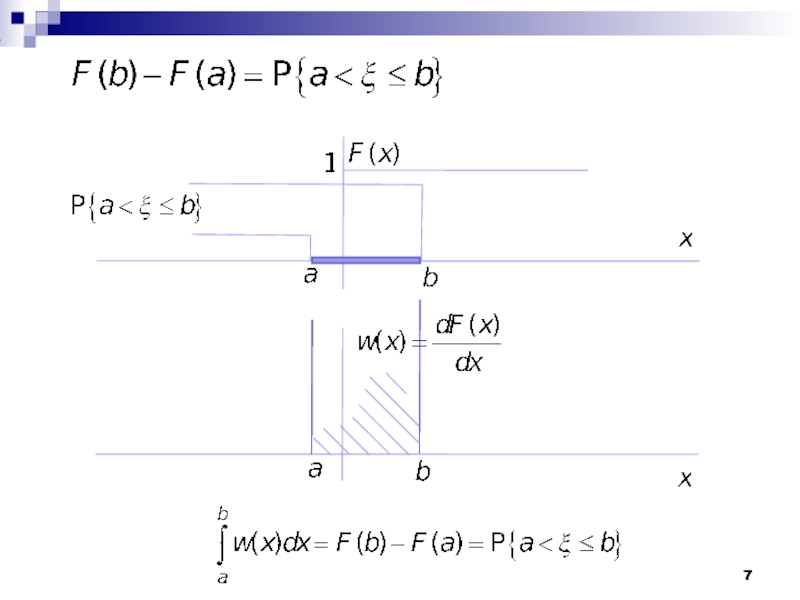
Слайд 6
− функция распределения с.в.
не убывает, но может оставаться постоянной на участках
оси
− плотность распределения вероятностей
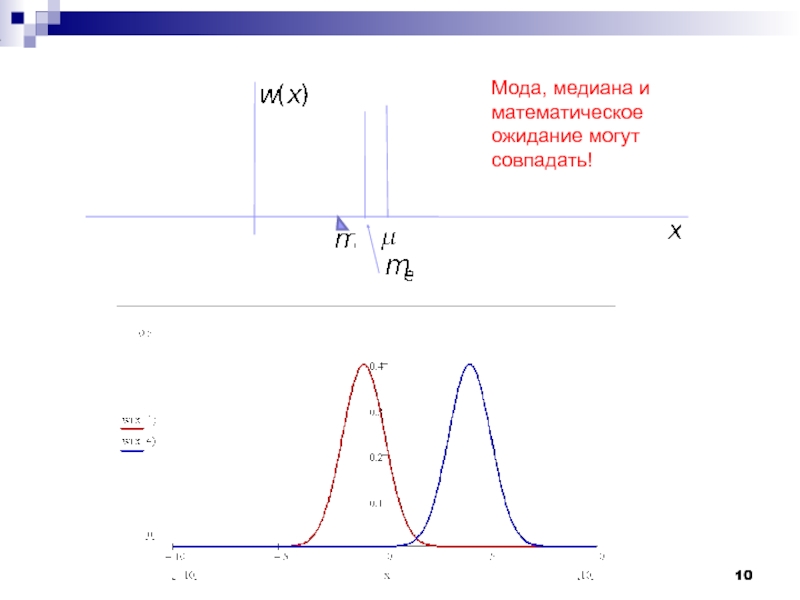
Слайд 9Числовые характеристики с.в.
− начальный момент k-го порядка
− начальный момент 1-го порядка,
математическое ожидание, «центр распределения»
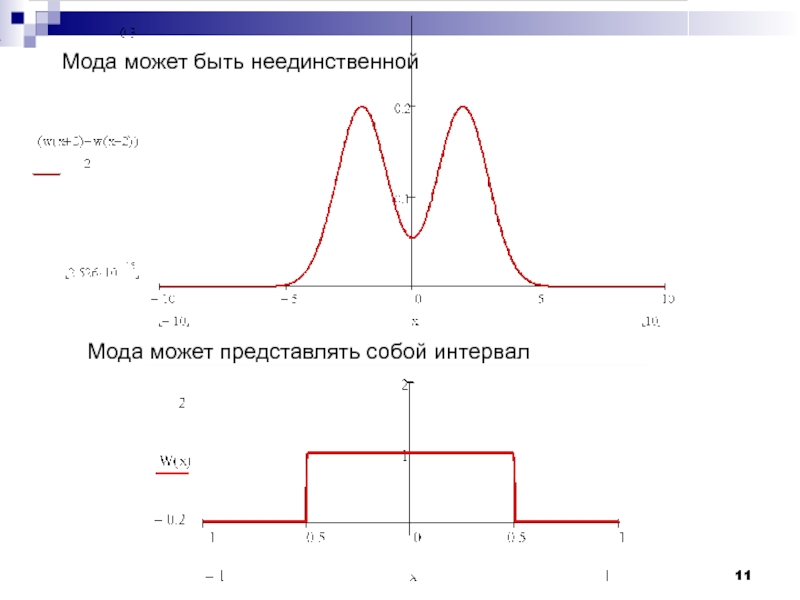
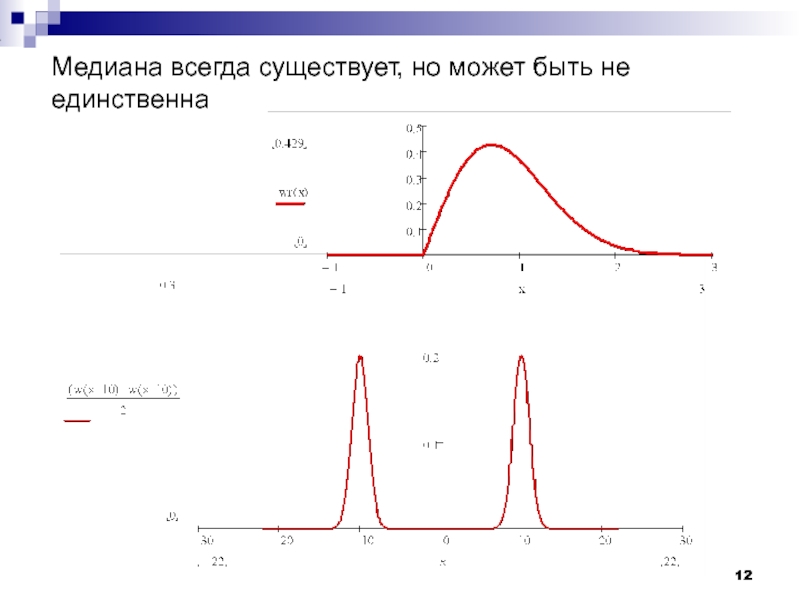
− мода
− медиана
Слайд 13
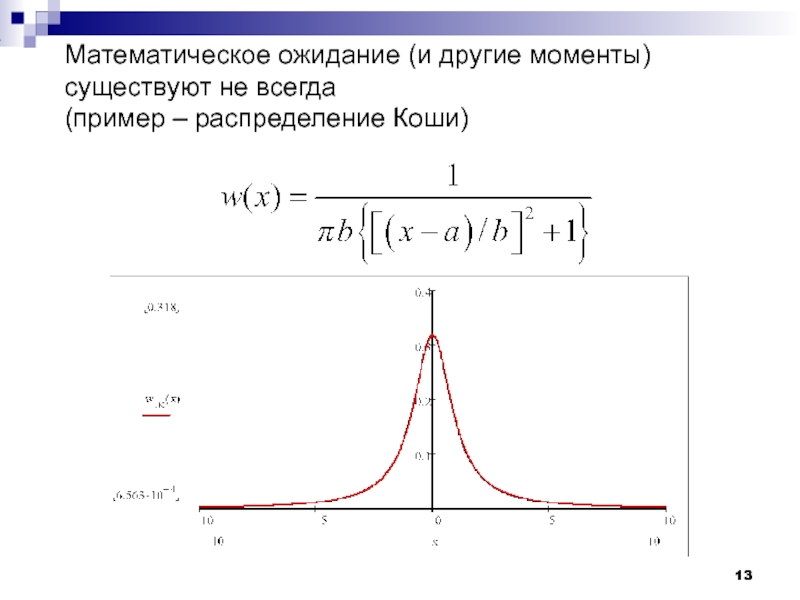
Математическое ожидание (и другие моменты) существуют не всегда
(пример – распределение
Коши)
Слайд 14
− центральный момент k-го порядка
− центральный момент 2-го порядка (дисперсия)
− среднеквадратическое
отклонение (СКО)
Слайд 15
− центральный момент 2-го порядка (дисперсия)
− среднеквадратическое отклонение (СКО)
− средний квадрат
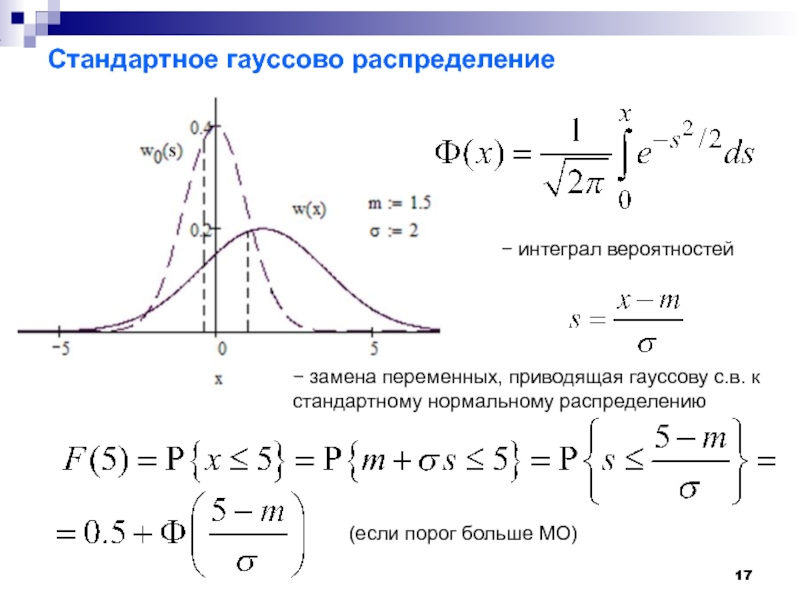
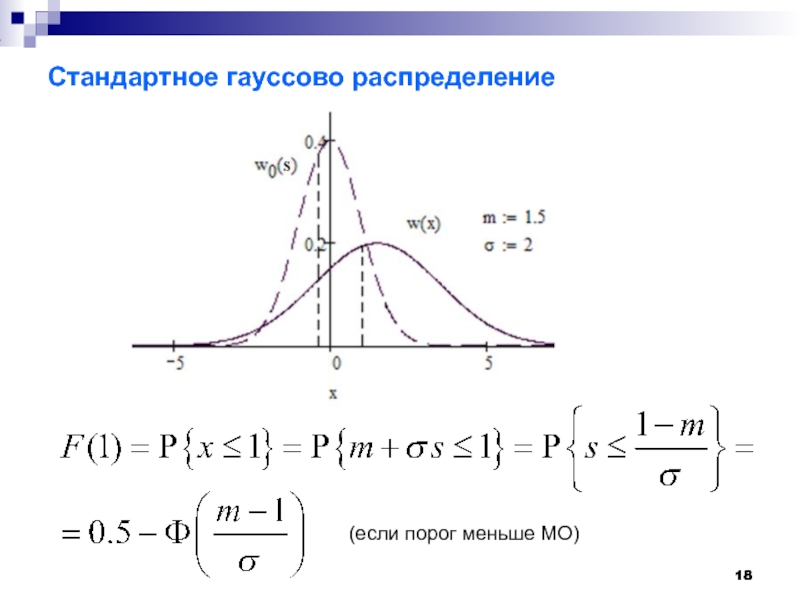
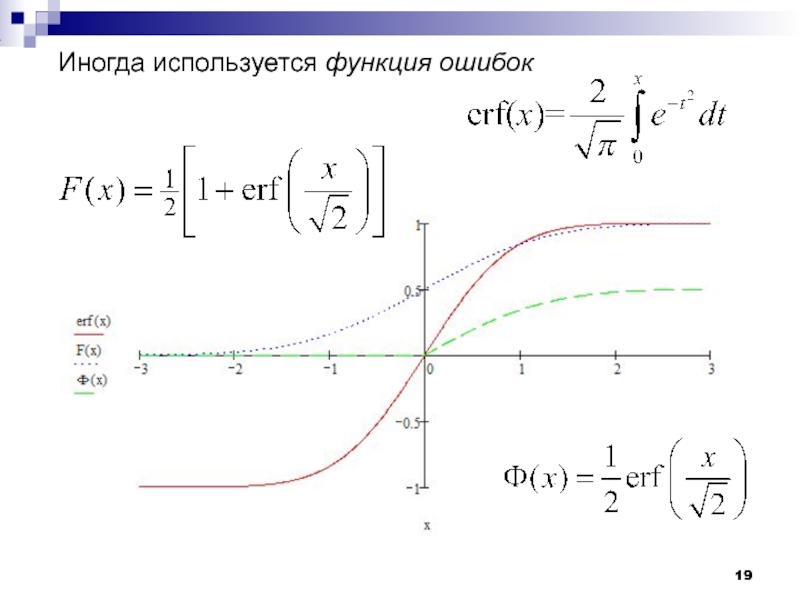
Слайд 17Стандартное гауссово распределение
− интеграл вероятностей
− замена переменных, приводящая гауссову с.в. к
стандартному нормальному распределению
(если порог больше МО)
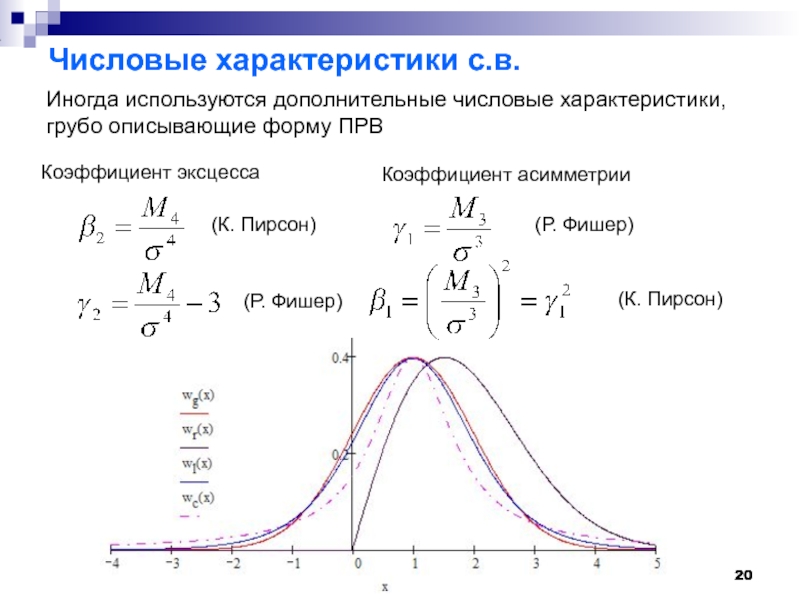
Слайд 20Числовые характеристики с.в.
Иногда используются дополнительные числовые характеристики, грубо описывающие форму ПРВ
Коэффициент
эксцесса
Коэффициент асимметрии
(К. Пирсон)
(Р. Фишер)
(Р. Фишер)
(К. Пирсон)
Слайд 26Числовые характеристики системы 2 случайных величин
Начальные смешанные моменты
Центральные смешанные моменты
Слайд 28Пример. Пара гауссовских случайных величин
коэффициент корреляции
При нулевом коэффициенте корреляции
Некоррелированные гауссовские с.в.
– независимы!
