- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математика Вавилона и Древнего Египта презентация
Содержание
- 1. Математика Вавилона и Древнего Египта
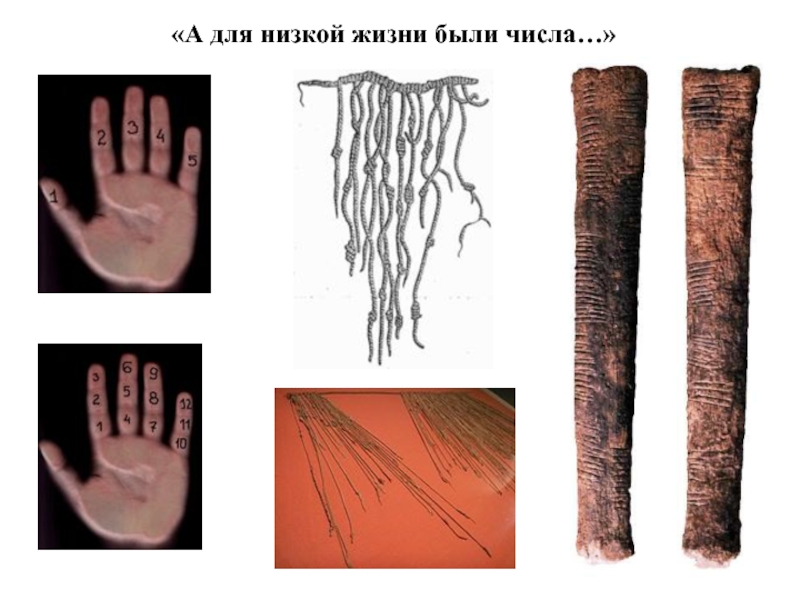
- 2. «А для низкой жизни были числа…»
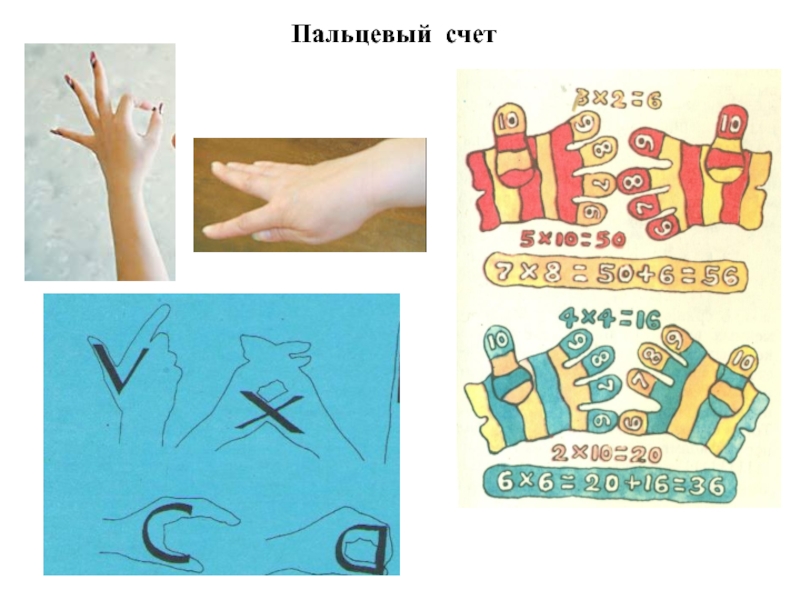
- 3. Пальцевый счет
- 4. Аддитивный II, VI, XX Принципы нумерации Субстрактивный
- 5. Две цивилизации Ван дер Варден Б.Л. Пробуждающаяся
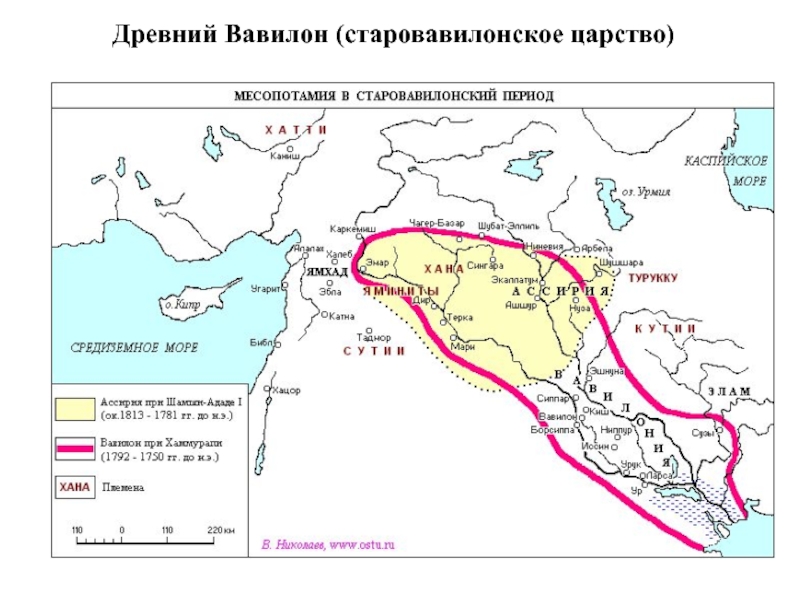
- 6. Древний Вавилон (старовавилонское царство)
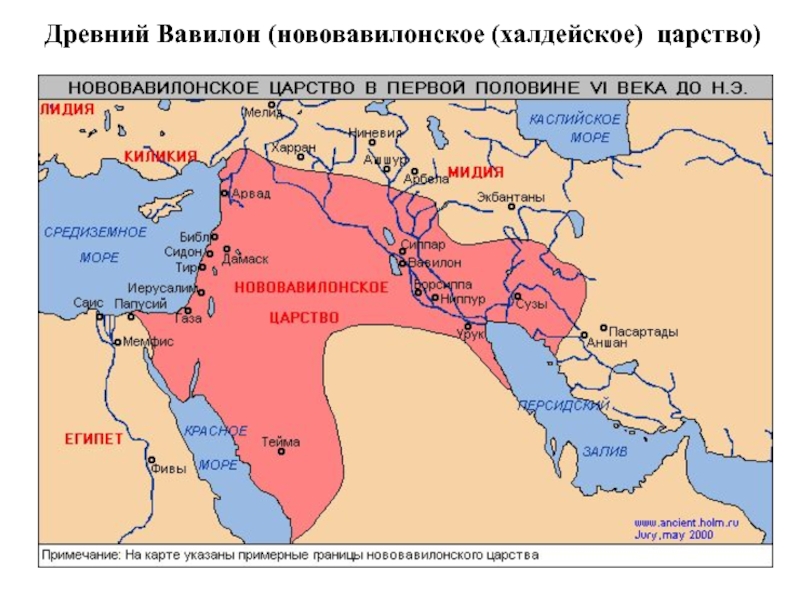
- 7. Древний Вавилон (нововавилонское (халдейское) царство)
- 8. Древний Вавилон (старовавилонское царство)
- 9. Древний Вавилон (нововавилонское (халдейское) царство)
- 11. Древний Вавилон 1900-1700 г. до н.э 2040 г. до н.э 500 г. до н.э.
- 12. Древний Вавилон
- 13. Древний Вавилон Вавилонская глиняная табличка, содержащая геометрические
- 14. Древний Вавилон - нумерация 92=60+32 444=420+24=7*60+24
- 15. Древний Вавилон - арифметика Произведения, Обратные значения,
- 16. Древний Вавилон (основные достижения) Зачатки линейной алгебры
- 17. Древний Вавилон (основные достижения) Геометрия пропорциональность
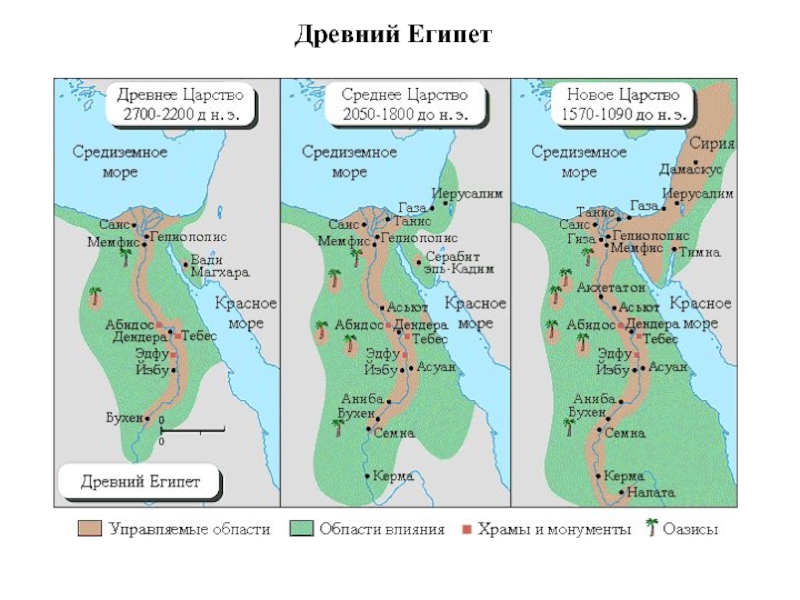
- 18. Древний Египет
- 19. Древний Египет
- 20. Древний Египет Меекс Д., Фавар-Меекс К. Повседневная жизнь египетских богов. – М.: Молодая гвардия, 2008
- 21. Древний Египет
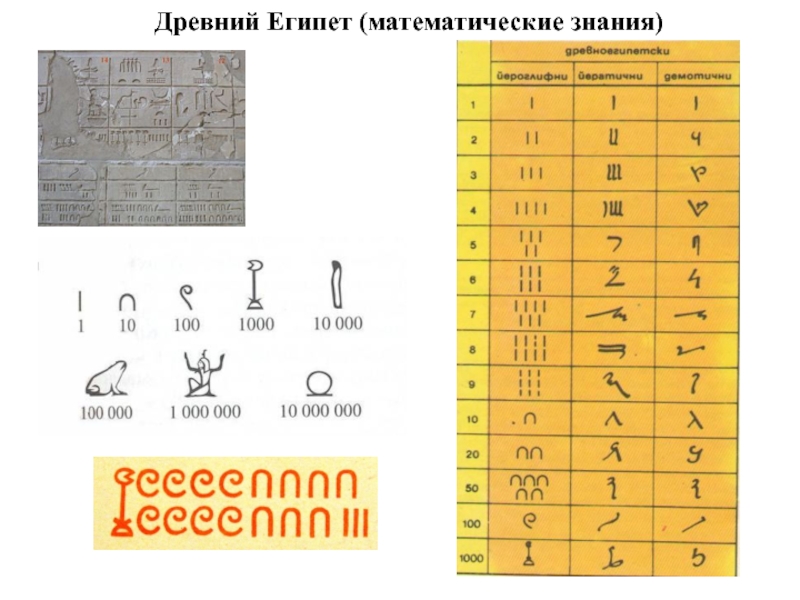
- 22. Древний Египет (математические знания)
- 23. Древний Египет (математические знания)
- 24. Задачи на «аха» Задача № 26 папируса
- 25. Древний Египет (математические знания) Геометрия
- 26. Древний Египет (математические знания) Геометрия
- 27. «Ещё нельзя говорить о математике как о
Слайд 4Аддитивный
II, VI, XX
Принципы нумерации
Субстрактивный
IV, IX, XL
Мультипликативный
двадцать, двести
Системы счисления
Непозиционная
Позиционная
MDCCLXXXII
3333= 3×1000 +
Слайд 5Две цивилизации
Ван дер Варден Б.Л. Пробуждающаяся наука. - М.: ГФМЛ, 1959
Выгодский М.Я. Арифметика и алгебра в древнем мире. – М.: Наука, 1967.
Нейгебауэр О. Точные науки в древности. – М.: Наука, 1968 (и позже)
Раик А.Е. Очерки по истории математики в древности. – Саранск: Мордовское кн. изд-во, 1967.
Раик А.Е. Две лекции о египетской и вавилонской математике // Историко-матем. исследования, в.XII. – М .: ГИФМЛ, 1959. – С. 271-320.
Слайд 13Древний Вавилон
Вавилонская глиняная табличка, содержащая геометрические задачи. Начало II тысячелетия до
Древневавилонский клинописный текст. На изображённом участке содержится 16 задач с решениями, относящихся к расчёту плотин, валов, колодцев. Задача, снабженная чертежом, относится к расчету кругового вала. Британский музей
Слайд 15Древний Вавилон - арифметика
Произведения,
Обратные значения,
Таблицы квадратных и кубических корней
Таблицы величин,
Таблицы чисел вида
таблицы эфемерид Солнца, Луны и планет
.
Основные достижения
правило приближённого вычисления квадратного корня
задачи на пропорции, среднее арифметическое
арифметическая и геометрическая прогрессии
задачи на проценты и сложные проценты
Слайд 17Древний Вавилон (основные достижения)
Геометрия
пропорциональность
теорема Пифагора
площади треугольника и
площадь круга и длина окружности с плохим приближением π=3
объемы призмы, цилиндра (площадь основания на высоту), неверные формулы для объема усеченного конуса и пирамиды
Аллен Дж. Д. Вавилонская математика
http://elenakosilova.narod.ru/studia3/math/translatio/babylon.htm
Слайд 20Древний Египет
Меекс Д., Фавар-Меекс К.
Повседневная жизнь египетских богов. – М.: Молодая
Слайд 24Задачи на «аха»
Задача № 26 папируса Ринда.
«Количество и его четвертая
Задача № 19 Московского папируса.
«1 и 1/2 кучи сосчитано вместе с 4, получается 10. Что есть куча? Подсчитай число, на которое 10 превышает 4. Выступает 6. Сколько раз надо взять 1 и 1/2, чтобы получить 1? Это 2*(1/3). Возьмем 2*(1/3) от 6. Это есть 4. 4 ты берешь. Ты нашел верно.»
Прогрессии
Слайд 25Древний Египет (математические знания)
Геометрия
Евдем Родосский (V в. до н.э.). «Геометрия была
Слайд 26Древний Египет (математические знания)
Геометрия
площади треугольников, прямоугольников, трапеций
приближённое вычисление площадей четырёхугольников
объемы кубов,
площадь круга S=(8d/9)2 π≈4(8/9)2=3, 1605…
правило нахождения объема усечённой пирамиды