- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы математического анализа презентация
Содержание
- 1. Основы математического анализа
- 2. Литературв Дискретная математика.Курс лекций / И.А. Палий.
- 3. Элементы линейной алгебры Алгебра матриц
- 4. Матрица Матрица A размера m×n – таблица
- 5. Элемент матрицы A, находящийся в i-ой
- 6. Матрица, в которой имеется только одна строка,
- 7. Квадратная матрица Матрица, в которой число
- 8. Диагональная матрица Диагональная матрица – квадратная
- 9. Единичная матрица Единичная матрица –диагональная матрица,
- 10. Верхней (нижней) треугольной матрицей называется квадратная
- 11. ОПЕРАЦИИ НАД МАТРИЦАМИ
- 12. Транспонирование матрицы Результат транспонирования матрицы
- 13. Умножение матрицы на число Результат
- 14. Сложение матриц Результат сложения двух
- 15. Вычитание матриц Результат вычитания двух
- 16. Умножение матриц Результат умножения матрицы
- 17. Умножение матриц
- 18. Свойства операций: 1. A+B= B+A 2.
- 19. ОПРЕДЕЛИТЕЛИ КВАДРАТНЫХ МАТРИЦ A –
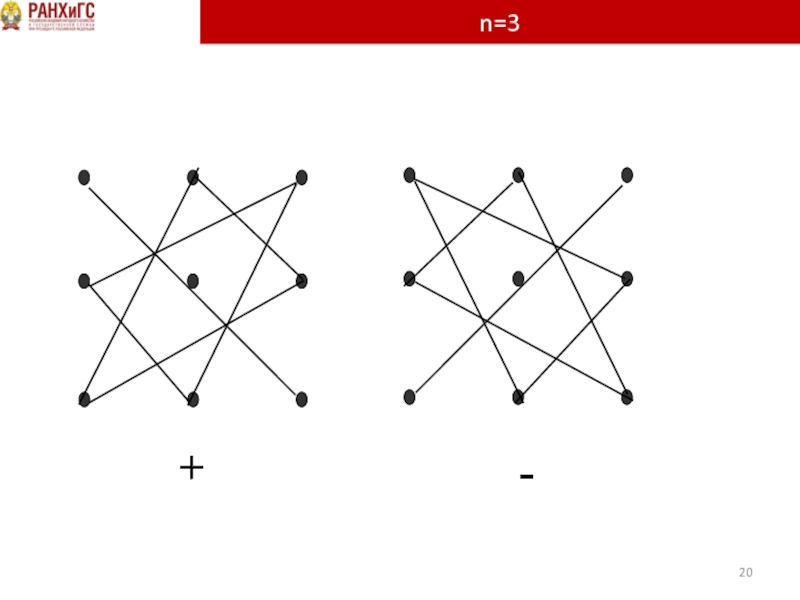
- 20. n=3
- 21. Минор Mij элемента aij матрицы A
- 22. Разложение определителя по строке (или столбцу):
- 23. Квадратная матрица, определитель которой равен нулю – вырожденная.
- 24. Спасибо за внимание!
Литературв Дискретная математика.Курс лекций / И.А. Палий. М.: Эксмо, 2008. Дискретная математика. Курс лекций и практических занятий/ С.Д. Шапорев. СПб.:БХВ-Петербург, 2007. Учебно-методическое пособие по математике. Математическая логика. Дискретная математика. Линейная алгебра
Слайд 1
Основы математического анализа
Зарубежное регионоведение
1 курс
Сафонова Татьяна Евгеньевна, к.ф.-м.н., доцент
Слайд 2Литературв
Дискретная математика.Курс лекций / И.А. Палий. М.: Эксмо, 2008.
Дискретная математика. Курс
лекций и практических занятий/ С.Д. Шапорев. СПб.:БХВ-Петербург, 2007.
Учебно-методическое пособие по математике. Математическая логика. Дискретная математика. Линейная алгебра / Под ред. А.Н. Данчула. М.: Изд-во РАГС, 2004.
Кремер Н.Ш. Высшая математика для бакалавриата экономических специальностей. М.: Юрайт, 2014.
Учебно-методическое пособие по математике. Математическая логика. Дискретная математика. Линейная алгебра / Под ред. А.Н. Данчула. М.: Изд-во РАГС, 2004.
Кремер Н.Ш. Высшая математика для бакалавриата экономических специальностей. М.: Юрайт, 2014.
Слайд 6Матрица, в которой имеется только одна строка, – вектор-строка
Матрица, в
которой есть только один столбец, – вектор-столбец
Слайд 7Квадратная матрица
Матрица, в которой число строк равно числу столбцов, –
квадратная матрица n-го порядка
Слайд 8Диагональная матрица
Диагональная матрица – квадратная матрица, у которой все элементы,
не принадлежащие главной диагонали, равны нулю
Главня диагональ матрицы – множество ее элементов, у которых номер строки равен номеру столбца
Главня диагональ матрицы – множество ее элементов, у которых номер строки равен номеру столбца
Слайд 9Единичная матрица
Единичная матрица –диагональная матрица, у которой все элементы, принадлежащие
главной диагонали, равны единице
Слайд 10
Верхней (нижней) треугольной матрицей называется квадратная матрица произвольного порядка, все элементы
которой, стоящие под (над) главной диагональю, равны нулю.
Нулевой матрицей называется матрица произвольного порядка, все элементы которой равны нулю.
Нулевой матрицей называется матрица произвольного порядка, все элементы которой равны нулю.
Слайд 12
Транспонирование матрицы
Результат транспонирования матрицы размера m×n – матрица размера n×m, столбцы
которой являются строками исходной матрицы и записаны в том же порядке.
B =AT [bij]n m =[aji]m n
B =AT [bij]n m =[aji]m n
Слайд 13
Умножение матрицы на число
Результат умножения матрицы размера m×n на число λ
– матрица того же размера, все элементы которой равны соответствующим элементам исходной матрицы, умноженным на это число. Bmn=λAmn [bij]mn =[λaij]mn
Слайд 14
Сложение матриц
Результат сложения двух матриц одинакового размера m×n – матрица того
же размера, все элементы которой равны сумме соответствующих элементов матриц-слагаемых. Cmn =Amn + Bmn [cij]mn =[aij+bij]mn
Слайд 15
Вычитание матриц
Результат вычитания двух матриц одинакового размера m×n – матрица того
же размера, все элементы которой равны разности соответствующих элементов матриц-слагаемых.
Cmn =Amn - Bmn
[cij]mn =[aij - bij]mn
Cmn =Amn - Bmn
[cij]mn =[aij - bij]mn
Слайд 16
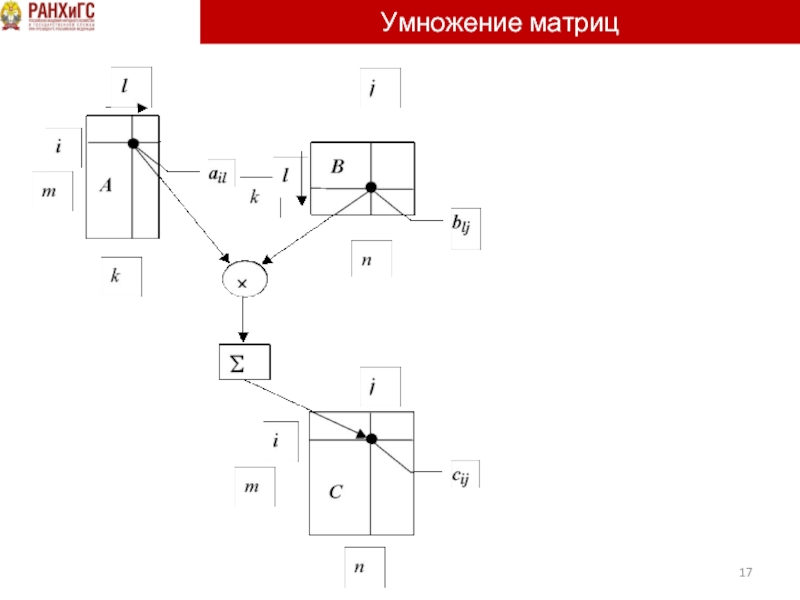
Умножение матриц
Результат умножения матрицы A размера m×k на матрицу B размера
k×n – матрица C размера m×n, каждый элемент которой cij равен сумме всех попарных произведений элементов, стоящих на одинаковых местах в i-ой строке матрицы A и j-ом столбце матрицы B.
Cmn =AmkBkn
Cmn =AmkBkn
Слайд 18Свойства операций:
1. A+B= B+A
2. (A+B)+C=A+(B+C)
3. λ(A+B)= λA+λB
4. A(B+C)=AB+AC (A+B)C=AC+BC
5. λ(AB) = (λA)B
= A(λB)
6. A(B C)=(AB)C
7. В общем случае AB≠BA
6. A(B C)=(AB)C
7. В общем случае AB≠BA
Слайд 19
ОПРЕДЕЛИТЕЛИ КВАДРАТНЫХ МАТРИЦ
A – квадратная матрица порядка n, ее определитель обозначается
det(A) или ⎜A⎪.
Если n =1, то⎜A⎪=⎜a11⎪=a11
Если n =2, то:
Если n =1, то⎜A⎪=⎜a11⎪=a11
Если n =2, то:
Слайд 21
Минор Mij элемента aij матрицы A n-го порядка – определитель матрицы
(n-1)-го порядка, полученной из A вычеркиванием i–ой строки и j–го столбца.
Алгебраическое дополнение Aij элемента aij матрицы A n-го порядка – его минор, взятый со знаком, определяемым по правилу шахматной доски
Алгебраическое дополнение Aij элемента aij матрицы A n-го порядка – его минор, взятый со знаком, определяемым по правилу шахматной доски
