правило Лопиталя.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основные теоремы о дифференцируемых функциях, правило Лопиталя. (Лекция 11) презентация
Содержание
- 1. Основные теоремы о дифференцируемых функциях, правило Лопиталя. (Лекция 11)
- 2. Теорема Ферма′ (Пьер Ферма). Пусть функция y
- 3. Доказательство Для определенности будем считать, что в
- 4. Пусть x ∈ (a, x0), то есть
- 5. Перейдем к пределу в (1) и рассмотрим
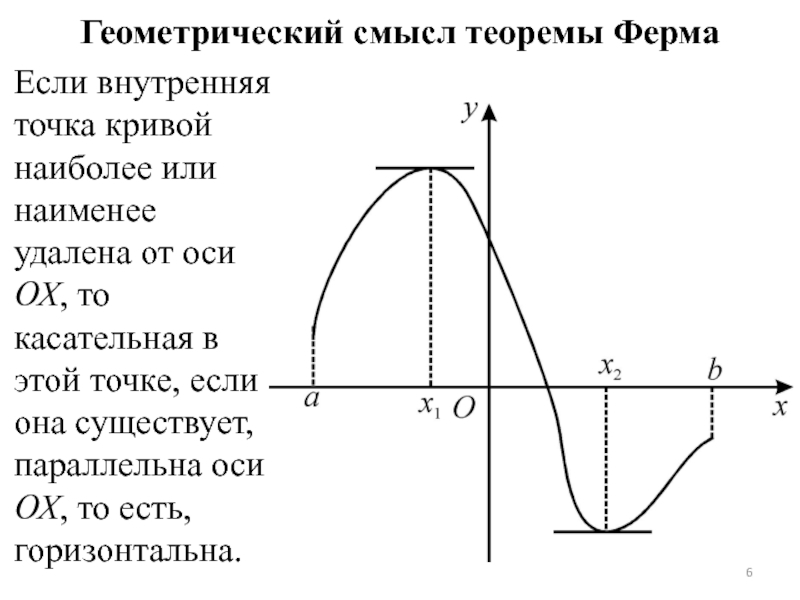
- 6. Геометрический смысл теоремы Ферма Если внутренняя точка
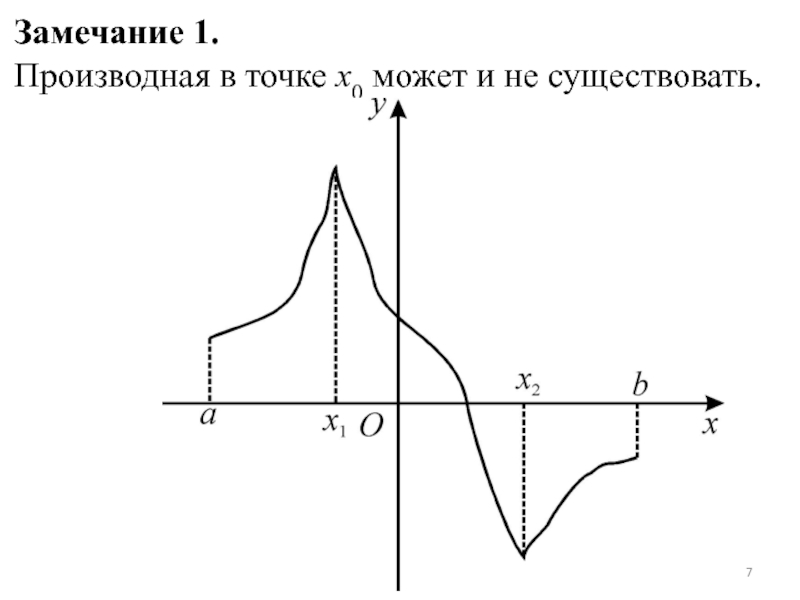
- 7. Замечание 1. Производная в точке x0 может и не существовать.
- 8. Замечание 2. Условие, что точка x0 внутренняя,
- 9. Определение. Пусть x0 – внутренняя точка из
- 10. Отыскание наибольшего и наименьшего значений функции Пусть
- 11. Может случиться так, что наибольшее или наименьшее значение принимается внутри отрезка [a,b] в точке x0.
- 12. Возможны два случая: а) f ′(x0) не
- 13. Алгоритм решения задачи: 1) Находим f
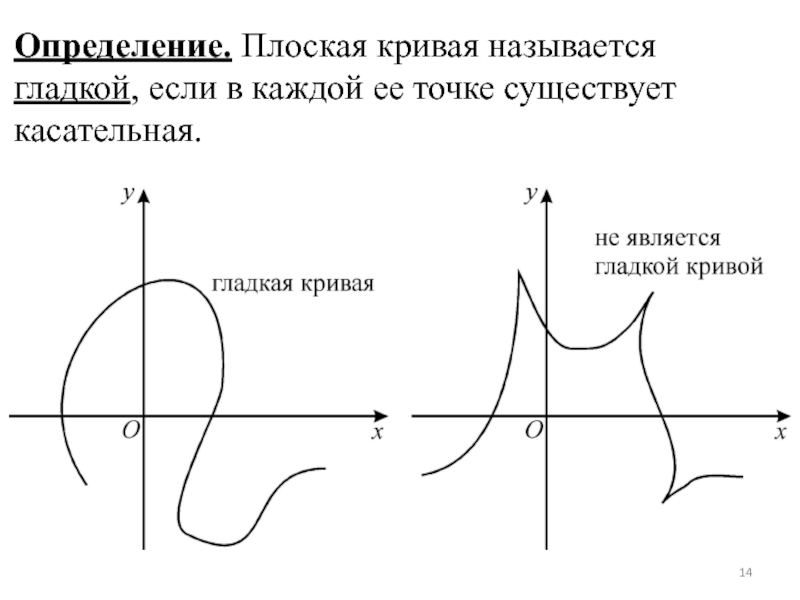
- 14. Определение. Плоская кривая называется гладкой, если в каждой ее точке существует касательная.
- 15. Теорема Ролля. Пусть функция y = f(x)
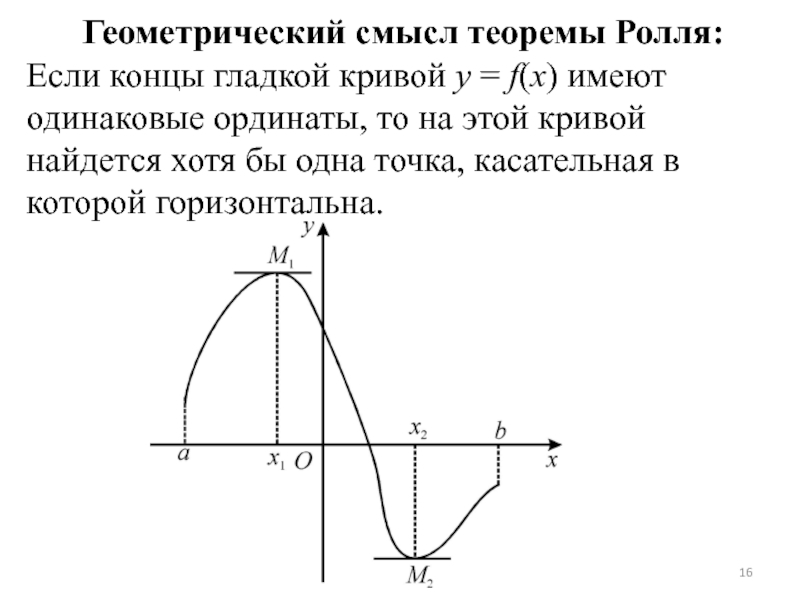
- 16. Геометрический смысл теоремы Ролля: Если концы гладкой
- 17. Доказательство Возможны два случая: а) функция на
- 18. b) функция не является постоянной на этом
- 20. Теорема Лагранжа. Пусть функция y = f(x)
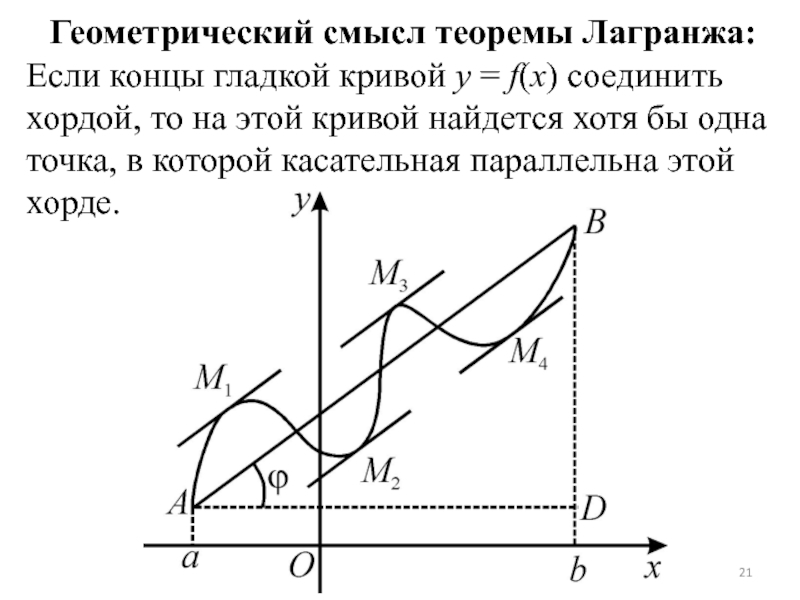
- 21. Геометрический смысл теоремы Лагранжа: Если концы гладкой
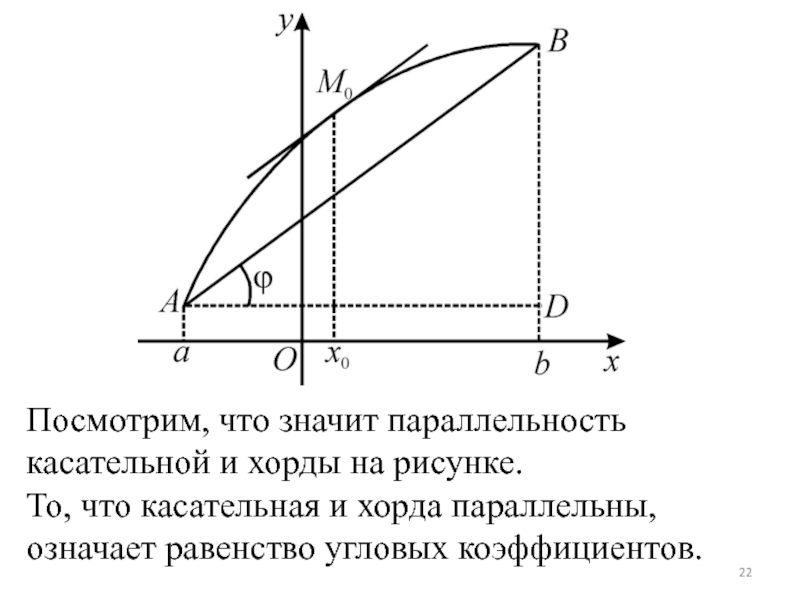
- 22. Посмотрим, что значит параллельность касательной и хорды
- 23. Пусть k1 - угловой коэффициент касательной, k2
- 24. Доказательство теоремы Лагранжа Рассмотрим вспомогательную функцию:
- 25. 3) ϕ(a) = ϕ(b). Действительно:
- 26. Замечание. Теорема Ролля является частным случаем
Слайд 2Теорема Ферма′ (Пьер Ферма). Пусть функция y = f(x) определена на
отрезке [a,b], и в некоторой внутренней точке этого отрезка принимает свое наибольшее или наименьшее значение, тогда, если производная в этой точке f ′(x0) существует, то она непременно = 0.
Слайд 3Доказательство
Для определенности будем считать, что в точке x0 функция принимает свое
наибольшее значение, то есть: ∀ x ∈ [a,b] ( f (x0) ≥ f (x)), иными словами:
f (x) - f (x0) ≤ 0. Пусть производная f ′(x) в точке x0
f ′(x0) = существует.
Требуется показать (!) f ′(x0) = 0.
Поскольку в точке x0 существует,
то стало быть существуют левый и правый преде-лы в этой точке и они равны по третьему крите-рию существования предела в точке, а именно:
f (x) - f (x0) ≤ 0. Пусть производная f ′(x) в точке x0
f ′(x0) = существует.
Требуется показать (!) f ′(x0) = 0.
Поскольку в точке x0 существует,
то стало быть существуют левый и правый преде-лы в этой точке и они равны по третьему крите-рию существования предела в точке, а именно:
Слайд 4Пусть x ∈ (a, x0), то есть находится слева от x0,
тогда x - x0 < 0 и поэтому:
Пусть x ∈ (x0,b), то есть находится справа от x0, тогда x - x0 > 0 и поэтому:
Пусть x ∈ (x0,b), то есть находится справа от x0, тогда x - x0 > 0 и поэтому:
Слайд 5Перейдем к пределу в (1) и рассмотрим левый предел:
С другой стороны,
переходя к пределу в (2) и рассматривая правый предел, получаем:
Из (*) заключаем, f ′(x0) ≥ 0 & f ′(x0) ≤ 0 ⇒ f ′(x0)=0.
Что и требовалось доказать.
Определение. Точка кривой называется внутренней точкой, если она не совпадает ни с одним из концов этой прямой.
Из (*) заключаем, f ′(x0) ≥ 0 & f ′(x0) ≤ 0 ⇒ f ′(x0)=0.
Что и требовалось доказать.
Определение. Точка кривой называется внутренней точкой, если она не совпадает ни с одним из концов этой прямой.
Слайд 6Геометрический смысл теоремы Ферма
Если внутренняя точка кривой наиболее или наименее удалена
от оси ОХ, то касательная в этой точке, если она существует, параллельна оси ОХ, то есть, горизонтальна.
Слайд 8Замечание 2.
Условие, что точка x0 внутренняя, является важным. Если x0 не
является внутренней точкой, то производная в ней не обязана быть равной нулю.
Пример
y = x2 на [1,2]
y′ = 2x наибольшее значение в точке 2, наименьшее в точке 1.
y′(1) = 2 ≠ 0.
y′(2) = 4 ≠ 0.
Слайд 9Определение. Пусть x0 – внутренняя точка из D(f) функции y =
f(x). Точка x0 называется критической точкой этой функции, если производная f ′(x0)=0, либо вовсе не существует. Те критические точки в которых производная = 0 называются стационарными.
x2, x3, x4 – стационарные точки
Слайд 10Отыскание наибольшего и наименьшего
значений функции
Пусть задана непрерывная функция y = f(x)
на [a,b]. Может случиться, что наибольшее или наименьшее значение принимается на концах этого отрезка.
Слайд 11Может случиться так, что наибольшее или наименьшее значение принимается внутри отрезка
[a,b] в точке x0.
Слайд 12Возможны два случая:
а) f ′(x0) не существует ⇒ x0 – критическая
точка;
b) f ′(x0) существует ⇒ (по теореме Ферма)
f ′(x0) = 0 ⇒ x0 – критическая стационарная точка.
Таким образом, внутренние точки, в которых достигается наибольшее или наименьшее значение нужно искать в критических точках.
Постановка задачи:
Найти наибольшее и наименьшее значения функции y = f (x) на [a,b].
Исходя из предыдущих рассуждений, получаем алгоритм.
b) f ′(x0) существует ⇒ (по теореме Ферма)
f ′(x0) = 0 ⇒ x0 – критическая стационарная точка.
Таким образом, внутренние точки, в которых достигается наибольшее или наименьшее значение нужно искать в критических точках.
Постановка задачи:
Найти наибольшее и наименьшее значения функции y = f (x) на [a,b].
Исходя из предыдущих рассуждений, получаем алгоритм.
Слайд 13Алгоритм решения задачи:
1) Находим f (a) и f (b) – значения
функции на концах отрезка.
2) Находим все критические точки данной функции на данном отрезке. Пусть это x1, x2, …, xn (в частности, их может и не быть).
3) Вычисляем f (x1), f (x2), …, f (xn).
4) Рассматриваем все полученные значения
f (a), f (b), f (x1), f (x2), …, f (xn) и выбираем из них наибольшее и наименьшее. Это и есть искомые значения.
2) Находим все критические точки данной функции на данном отрезке. Пусть это x1, x2, …, xn (в частности, их может и не быть).
3) Вычисляем f (x1), f (x2), …, f (xn).
4) Рассматриваем все полученные значения
f (a), f (b), f (x1), f (x2), …, f (xn) и выбираем из них наибольшее и наименьшее. Это и есть искомые значения.
Слайд 14Определение. Плоская кривая называется гладкой, если в каждой ее точке существует
касательная.
Слайд 15Теорема Ролля. Пусть функция y = f(x) определена на отрезке [a,b],
и удовлетворяет трем условиям:
1) f(x) непрерывна на отрезке [a,b].
2) f(x) дифференцируема на (a,b).
3) f(a) = f(b).
Тогда внутри отрезка [a,b] найдется хотя бы одна точка x0, в которой f ′(x0) = 0.
1) f(x) непрерывна на отрезке [a,b].
2) f(x) дифференцируема на (a,b).
3) f(a) = f(b).
Тогда внутри отрезка [a,b] найдется хотя бы одна точка x0, в которой f ′(x0) = 0.
Слайд 16Геометрический смысл теоремы Ролля:
Если концы гладкой кривой y = f(x) имеют
одинаковые ординаты, то на этой кривой найдется хотя бы одна точка, касательная в которой горизонтальна.
Слайд 17Доказательство
Возможны два случая:
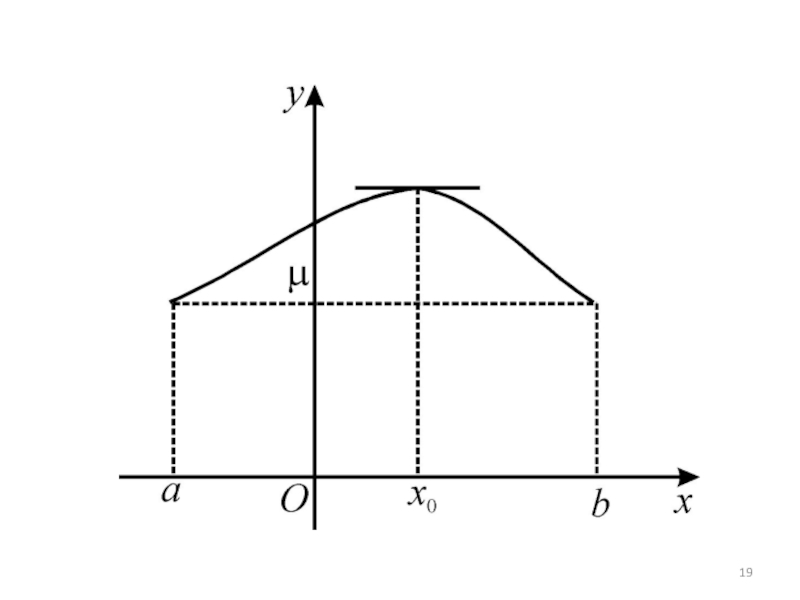
а) функция на этом отрезке постоянна, т.е.
∀ x ∈
[a,b] ( f(x) = f(a) = f(b) = μ).
В этом случае роль точки x0 может играть любая точка данного отрезка. Тогда f ′(x0) = 0 как производная константы.
В этом случае роль точки x0 может играть любая точка данного отрезка. Тогда f ′(x0) = 0 как производная константы.
Слайд 18b) функция не является постоянной на этом отрезке. В этом случае
внутри [a,b] эта функция принимает значения, отличные от f(a) = f(b) = μ.
Для определенности будем считать, что в некоторых внутренних точках функция принимает положительные значения (если отрицательные, то рассуждения аналогичны). Но тогда свое наибольшее значение функция принимает в некоторой внутренней точке x0 больше μ.
По условия f ′(x0) существует. Тогда по теореме Ферма f ′(x0) = 0.
Что и требовалось доказать.
Для определенности будем считать, что в некоторых внутренних точках функция принимает положительные значения (если отрицательные, то рассуждения аналогичны). Но тогда свое наибольшее значение функция принимает в некоторой внутренней точке x0 больше μ.
По условия f ′(x0) существует. Тогда по теореме Ферма f ′(x0) = 0.
Что и требовалось доказать.
Слайд 20Теорема Лагранжа. Пусть функция y = f(x) определена на отрезке [a,b],
и удовлетворяет двум условиям:
1) f(x) непрерывна на отрезке [a,b].
2) f(x) дифференцируема на (a,b).
Тогда внутри отрезка [a,b] найдется хотя бы одна точка x0, в которой:
f(b) – f(a) = f ′(x0)(b – a).
1) f(x) непрерывна на отрезке [a,b].
2) f(x) дифференцируема на (a,b).
Тогда внутри отрезка [a,b] найдется хотя бы одна точка x0, в которой:
f(b) – f(a) = f ′(x0)(b – a).
Слайд 21Геометрический смысл теоремы Лагранжа:
Если концы гладкой кривой y = f(x) соединить
хордой, то на этой кривой найдется хотя бы одна точка, в которой касательная параллельна этой хорде.
Слайд 22Посмотрим, что значит параллельность касательной и хорды на рисунке.
То, что касательная
и хорда параллельны, означает равенство угловых коэффициентов.
Слайд 23Пусть k1 - угловой коэффициент касательной,
k2 - хорды.
k1 = f ′(x0).
k2
= tgϕ = BD/AD = .
Так как k1 = k2, следовательно:
= f ′(x0).
Или
f(b) – f(a) = f ′(x0)(b – a).
Так как k1 = k2, следовательно:
= f ′(x0).
Или
f(b) – f(a) = f ′(x0)(b – a).
Слайд 24Доказательство теоремы Лагранжа
Рассмотрим вспомогательную функцию:
ϕ(x) = f(x) – f(a) –
(x – a).
Эта функция определена на отрезке [a,b], и удовлетворяет трем условиям теоремы Ролля:
1) ϕ(x) непрерывна на отрезке [a,b] как сумма напрерывных на этом отрезке функций.
2) ϕ(x) дифференцируема на (a,b). Действитель-но, ее производная существует и равна:
ϕ′(x) = f ′(x) – .
Эта функция определена на отрезке [a,b], и удовлетворяет трем условиям теоремы Ролля:
1) ϕ(x) непрерывна на отрезке [a,b] как сумма напрерывных на этом отрезке функций.
2) ϕ(x) дифференцируема на (a,b). Действитель-но, ее производная существует и равна:
ϕ′(x) = f ′(x) – .
Слайд 253) ϕ(a) = ϕ(b). Действительно:
ϕ(a) = f(a) –
f(a) – (a – a) = 0.
ϕ(b) = f(b) – f(a) – (b – a) = 0.
Тогда по теореме Ролля найдется такая точка
∃ x0 ∈ (a,b), в которой ϕ′(x0) = 0, то есть:
ϕ′(x) = f ′(x) – = 0.
Или
f (b) – f (a) = f ′(x0)(b – a).
Что и требовалось доказать.
ϕ(b) = f(b) – f(a) – (b – a) = 0.
Тогда по теореме Ролля найдется такая точка
∃ x0 ∈ (a,b), в которой ϕ′(x0) = 0, то есть:
ϕ′(x) = f ′(x) – = 0.
Или
f (b) – f (a) = f ′(x0)(b – a).
Что и требовалось доказать.
Слайд 26Замечание.
Теорема Ролля является частным случаем теоремы Лагранжа, или иными словами теорема
Лагранжа является обобщением теоремы Ролля.
Действительно, в том частном случае, когда
f (b) = f (a)
из теоремы Лагранжа:
f (b) – f (a) = f ′(x0)(b – a),
следует, что f ′(x0) = 0.
Действительно, в том частном случае, когда
f (b) = f (a)
из теоремы Лагранжа:
f (b) – f (a) = f ′(x0)(b – a),
следует, что f ′(x0) = 0.

![Теорема Ферма′ (Пьер Ферма). Пусть функция y = f(x) определена на отрезке [a,b], и в](/img/tmb/4/336899/780de2bea4e22bce1a0a0b339a9a0d92-800x.jpg)





![Отыскание наибольшего и наименьшегозначений функцииПусть задана непрерывная функция y = f(x) на [a,b]. Может случиться,](/img/tmb/4/336899/485c8cd03e72f9de85d690ae9ee39a4b-800x.jpg)
![Может случиться так, что наибольшее или наименьшее значение принимается внутри отрезка [a,b] в точке x0.](/img/tmb/4/336899/a10a551fddecef8348f4d42d4f7105f1-800x.jpg)


![Теорема Ролля. Пусть функция y = f(x) определена на отрезке [a,b], и удовлетворяет трем условиям:1)](/img/tmb/4/336899/6b97794d628ae3be6761d15c377d84de-800x.jpg)
![ДоказательствоВозможны два случая:а) функция на этом отрезке постоянна, т.е.∀ x ∈ [a,b] ( f(x) =](/img/tmb/4/336899/e520738a59c3445f0708661c104236e4-800x.jpg)
![b) функция не является постоянной на этом отрезке. В этом случае внутри [a,b] эта функция](/img/tmb/4/336899/1f841922f717ef00cdbafcc225948b73-800x.jpg)
![Теорема Лагранжа. Пусть функция y = f(x) определена на отрезке [a,b], и удовлетворяет двум условиям:1)](/img/tmb/4/336899/feb9cd090603e106b4eb0ffc02b8a3ed-800x.jpg)