- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Определённый интеграл презентация
Содержание
- 1. Определённый интеграл
- 2. Понятие о криволинейной трапеции Фигура, ограниченная неотрицательной
- 3. Задачи, приводящие к понятию определённого интеграла Для
- 4. Понятие определённого интеграла Предел такой суммы называют
- 5. Геометрический и физический смысл определённого интеграла
- 6. Формула Ньютона-Лейбница
- 7. Вычисление определённого интеграла
- 8. Примеры вычисления определённых интегралов
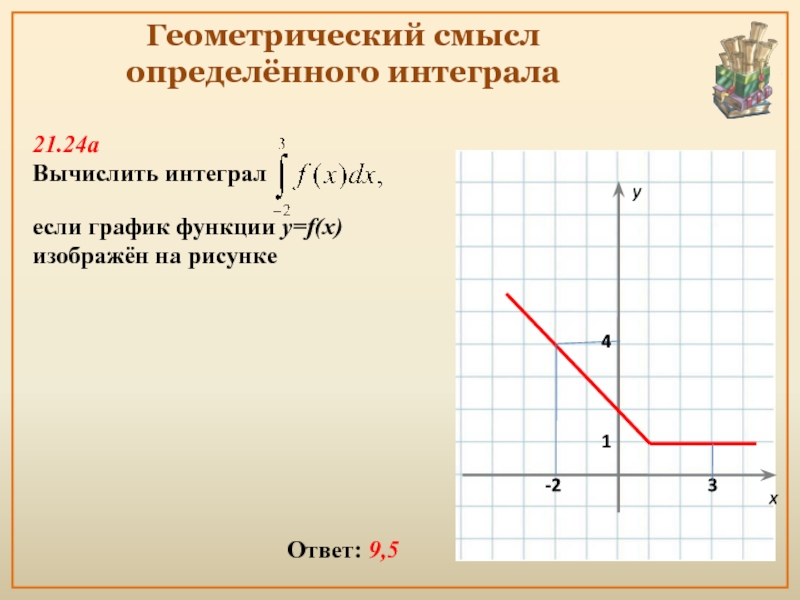
- 9. Геометрический смысл определённого интеграла Ответ: 9,5
- 10. Физический смысл определённого интеграла 21.40а Материальная точка
- 11. Физический смысл определённого интеграл 21.42а Дан прямолинейный
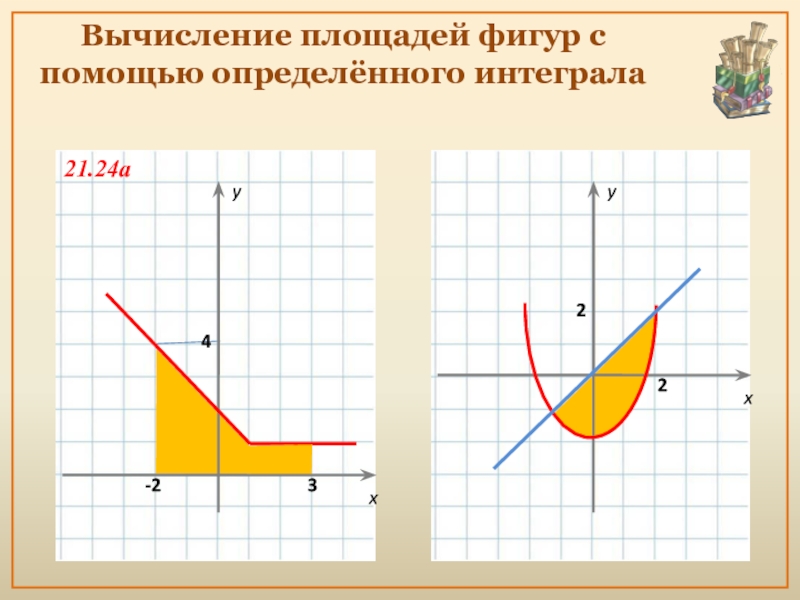
- 12. Вычисление площадей фигур с помощью определённого интеграла
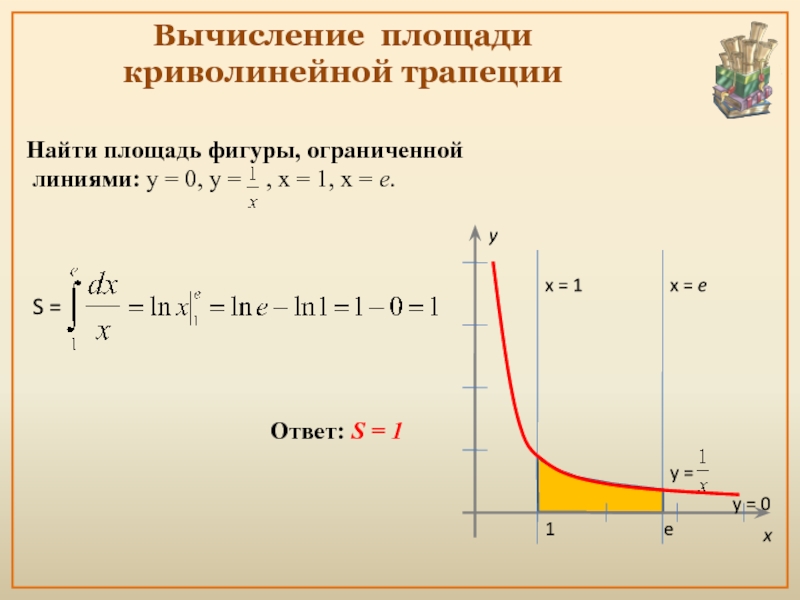
- 13. Вычисление площади криволинейной трапеции S = Ответ: S = 1
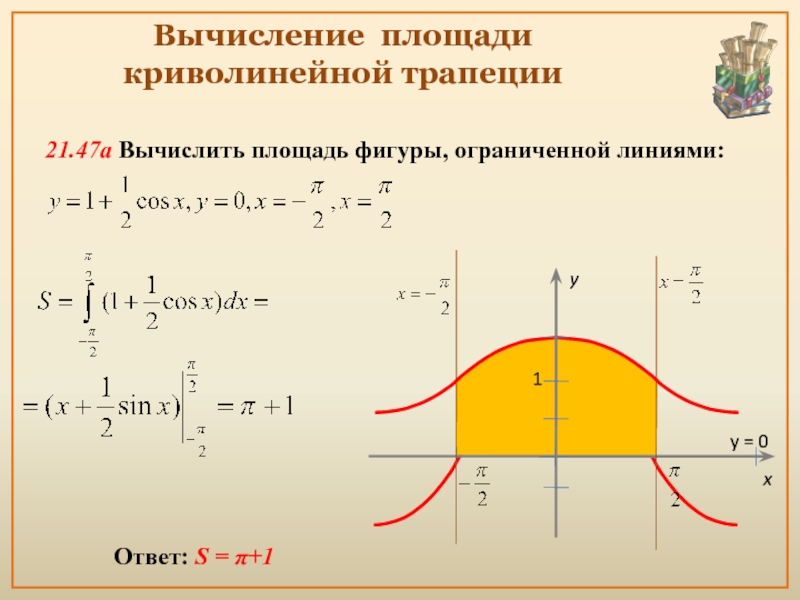
- 14. Вычисление площади криволинейной трапеции Ответ: S = π+1
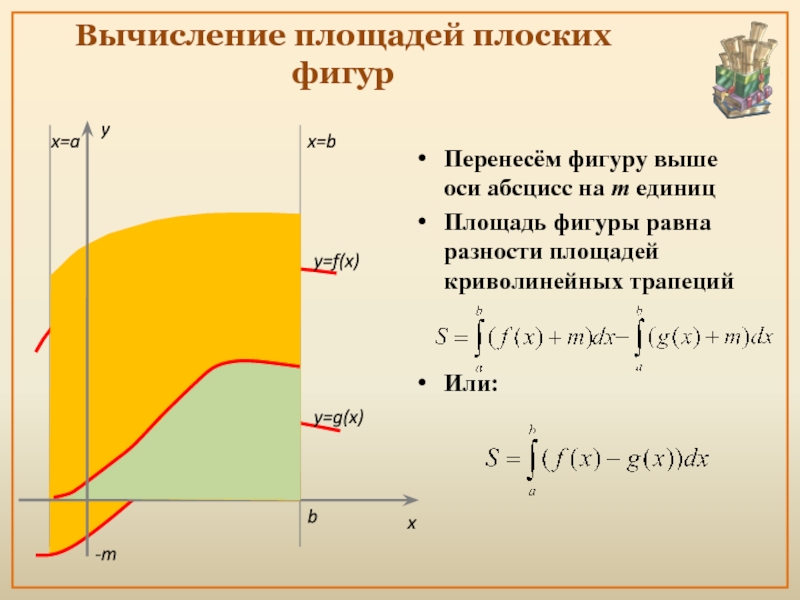
- 15. Вычисление площадей плоских фигур Перенесём фигуру выше
- 16. Вычисление площадей плоских фигур Вычислить площадь фигуры,
- 17. Рефлексия Криволинейная трапеция Формула Ньютона-Лейбница Геометрический и
- 18. Формула Ньютона-Лейбница
- 19. Формула Ньютона-Лейбница Ньютон открыл новый метод раньше,
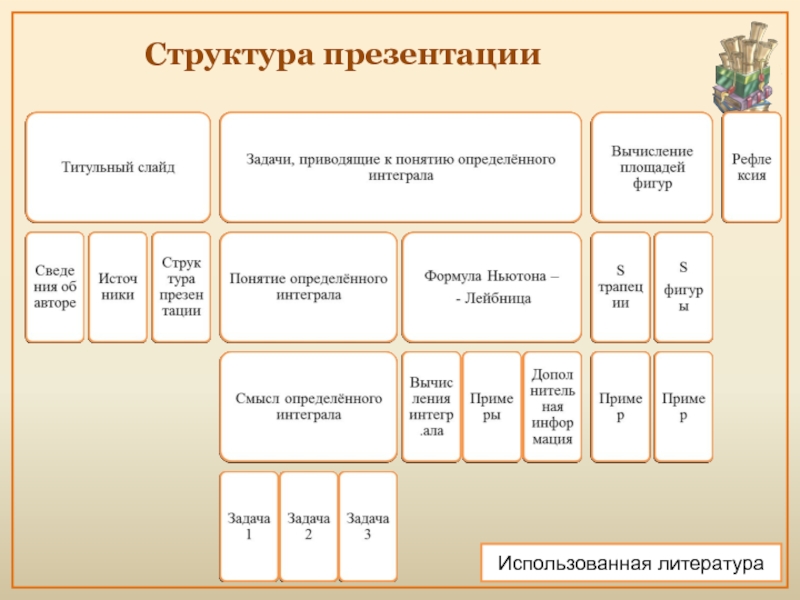
- 20. Структура презентации Использованная литература
- 21. Использованные ресурсы А.Г. Мордкович, П.В. Семёнов. Алгебра
Слайд 2Понятие о криволинейной трапеции
Фигура, ограниченная неотрицательной на отрезке [a; b] функцией
криволинейной трапецией
a
b
Слайд 3Задачи, приводящие к понятию определённого интеграла
Для функции y=f(x) на отрезке [a;b]:
Разбить
Составить сумму Sn =f(x0)·∆x0+…+ f(xn)·∆xn
Вычислить предел этой суммы при n→∞
Слайд 4Понятие определённого интеграла
Предел такой суммы называют
определённым интегралом по отрезку [a;b]:
Напоминание
Стиллизованная буква S (сумма)
Слайд 10Физический смысл определённого интеграла
21.40а Материальная точка движется по прямой со скоростью,
Какой путь пройдёт точка за 3 секунды,
считая от начала движения (t=0)?
Ответ: 12см
Слайд 11Физический смысл определённого интеграл
21.42а Дан прямолинейный неоднородный стержень [0;6], его плотность
Найдите массу стержня.
Ответ: 96
Слайд 15Вычисление площадей плоских фигур
Перенесём фигуру выше оси абсцисс на m единиц
Площадь
Или:
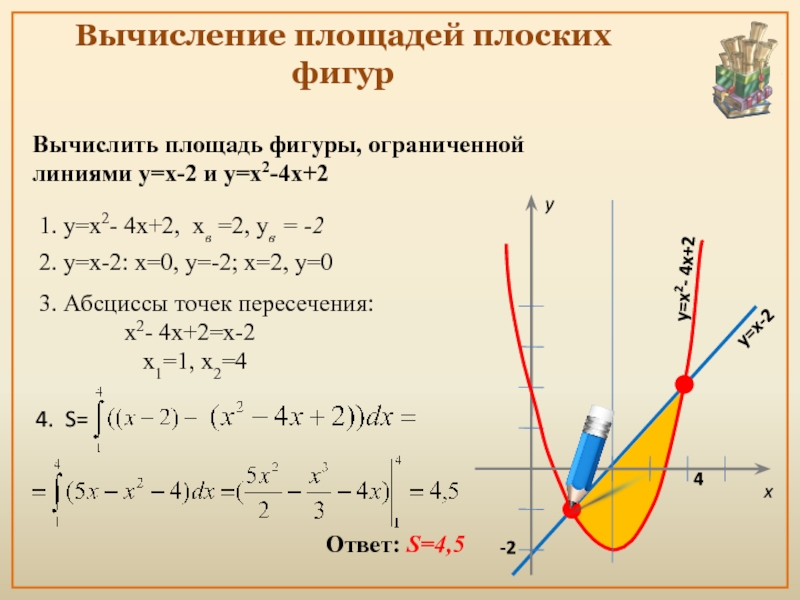
Слайд 16Вычисление площадей плоских фигур
Вычислить площадь фигуры, ограниченной
линиями y=x-2 и y=x2-4x+2
1.
3. Абсциссы точек пересечения:
x2- 4x+2=x-2
х1=1, х2=4
4. S=
Ответ: S=4,5
2. у=х-2: х=0, у=-2; х=2, у=0
Слайд 17Рефлексия
Криволинейная трапеция
Формула Ньютона-Лейбница
Геометрический и физический смысл определённого интеграла
Формула для вычисления площади
Слайд 19Формула Ньютона-Лейбница
Ньютон открыл новый метод раньше, но
опубликовал его позже Лейбница,
«Надеюсь, что я при этом не написал ничего,
что было бы тебе неприятно, если же это
случилось, то прошу сообщить, потому что
друзья мне дороже математических открытий»
Лейбниц ответил в резкой форме. Распря двух
гениев дорого обошлась науке: английская
математическая школа увяла на целый век,
а европейская проигнорировала многие
выдающиеся идеи Ньютона.
Спор тянулся почти 40 лет, пока аббат Конти не
сообщил Ньютону: «Лейбниц умер – диспут окончен»
Слайд 21Использованные ресурсы
А.Г. Мордкович, П.В. Семёнов. Алгебра и начала анализа. Учебник (профильный
А.Г. Мордкович, Л.О. Денищева и др. Алгебра и начала анализа. Задачник (профильный уровень)
Картинка "книги“
Материал Википедии Лейбниц Материал Википедии Лейбниц Ньютон
Рисунок карандаш
Значок Информация
Видео Величайший из учёных – Исаак Ньютон

![Понятие о криволинейной трапецииФигура, ограниченная неотрицательной на отрезке [a; b] функцией y=f(x) и прямыми y=0,](/img/tmb/3/247688/0f901eaf580a93b9ed8174f1e239a6d6-800x.jpg)
![Задачи, приводящие к понятию определённого интегралаДля функции y=f(x) на отрезке [a;b]:Разбить отрезок [a;b] на n](/img/tmb/3/247688/f3c814e900b50071848ade0f6ce0f071-800x.jpg)
![Понятие определённого интегралаПредел такой суммы называют определённым интегралом по отрезку [a;b]:Напоминание о слагаемых вида f(xn)∆xn](/img/tmb/3/247688/bfdaadf88bd22b4a2380fb7f485f84b0-800x.jpg)





![Физический смысл определённого интеграл21.42а Дан прямолинейный неоднородный стержень [0;6], его плотность в точке х определяется](/img/tmb/3/247688/ff13cdff689f335d4fdac70384b638e5-800x.jpg)