- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Описательная статистика презентация
Содержание
- 1. Описательная статистика
- 2. План лекции: Показатели центральной тенденции. Среднее арифметическое,
- 3. Показатели центральной тенденции. Среднее арифметическое, его свойства.
- 4. Средняя арифметическая ( х )
- 5. Для негруппированных данных эта величина определяется
- 6. Для данных, группируемых с учетом повторяемости или
- 7. Свойства среднего арифметического: 1. Если каждую
- 8. 2. Если каждую варианту совокупности разделить или
- 9. 3. Сумма произведений отклонений вариант от их
- 10. 4. Сумма квадратов отклонений вариант
- 11. Мода, медиана. Квартили. Соотношение между показателями центральной тенденции.
- 12. Медиана эмпирического распределения (Me) (от лат. Mediana
- 13. Если выборка распределена в вариационный ряд, медиана
- 14. Мода (Mo) – величина, которая встречается в
- 15. Квантили - структурные средние характеристики вариационного ряда,
- 16. Квартиль – величина, отсекающая 1/4
- 17. Показатели изменчивости
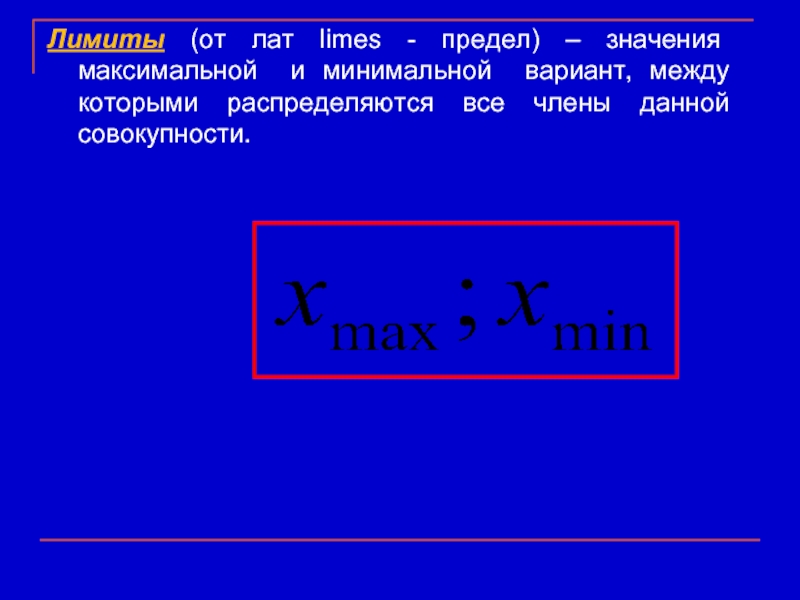
- 18. Лимиты (от лат limes - предел) –
- 19. Размах вариации – показатель, характеризующий варьирование признаков.
- 20. Дисперсия (от лат. Dispersion - рассеяние) или
- 21. Знак суммирования произведений отклонений вариант xi от
- 22. Свойства дисперсии: 1. Если каждую варианту
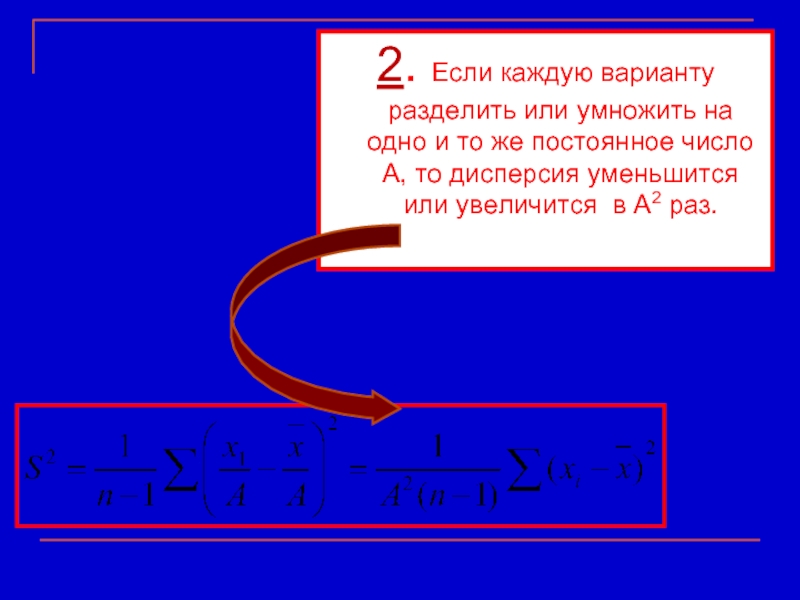
- 23. 2. Если каждую варианту разделить или умножить
- 24. Среднее квадратическое отклонение (Sx) Характеризует величину
- 25. Показатель, предложенный К. Пирсеном –обозначаемый буквой V (или CV) называется коэффициентом вариации.
- 26. В качестве констант, характеризующих случайную величину, можно
- 27. Проверка нормальности распределения с помощью показателей асимметрии
- 28. Асимметрия или коэффициент асимметрии (термин был впервые
- 29. Асимметрия или коэффициент асимметрии (термин был впервые
- 31. Асимметрия ряда выражается графически в виде скошенной
- 32. Коэффициент ассиметрии – величина безразмерная, может принимать
- 33. Асимметрию называют правосторонней или положительной, если вершина
- 34. Эксцесс Термин был впервые введен Пирсоном,
- 35. Эксцесс Термин был впервые введен Пирсоном,
- 37. Если эксцесс значимо отличен от 0, то
- 39. Благодарю за внимание!
Слайд 2План лекции:
Показатели центральной тенденции. Среднее арифметическое, его свойства.
Мода, медиана. Квартили. Соотношение
Показатели изменчивости: размах, дисперсия, среднее квадратическое отклонение, коэффициент вариации. Свойства дисперсии.
Показатели ассиметрии и эксцесса.
Слайд 4
Средняя арифметическая ( х ) – одна из основных характеристик вариационного
Слайд 5
Для негруппированных данных эта величина определяется как сумма всех членов совокупности
где:
- значения вариант
- знак суммирования вариант в пределах от первой до n- й варианты
- общее число вариант
Слайд 6Для данных, группируемых с учетом повторяемости или веса (pi) отдельных вариант
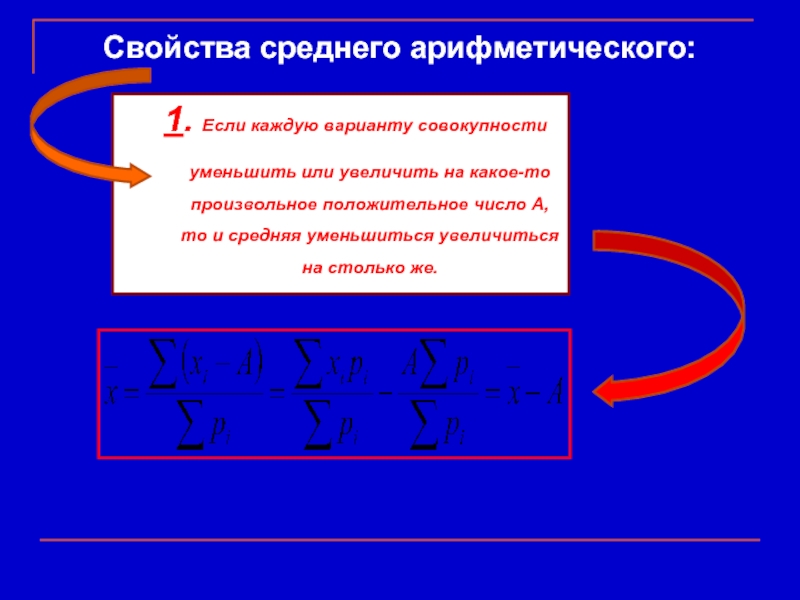
Слайд 7Свойства среднего арифметического:
1. Если каждую варианту совокупности уменьшить или увеличить на
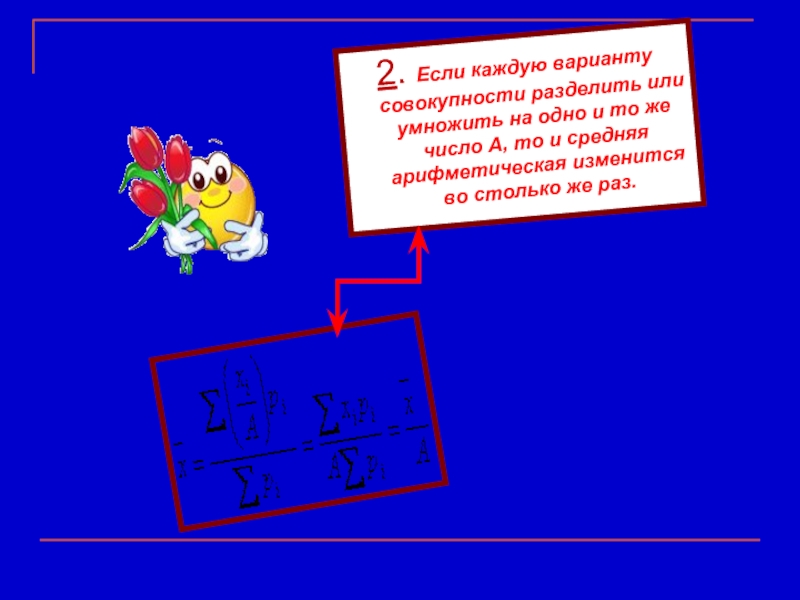
Слайд 82. Если каждую варианту совокупности разделить или умножить на одно и
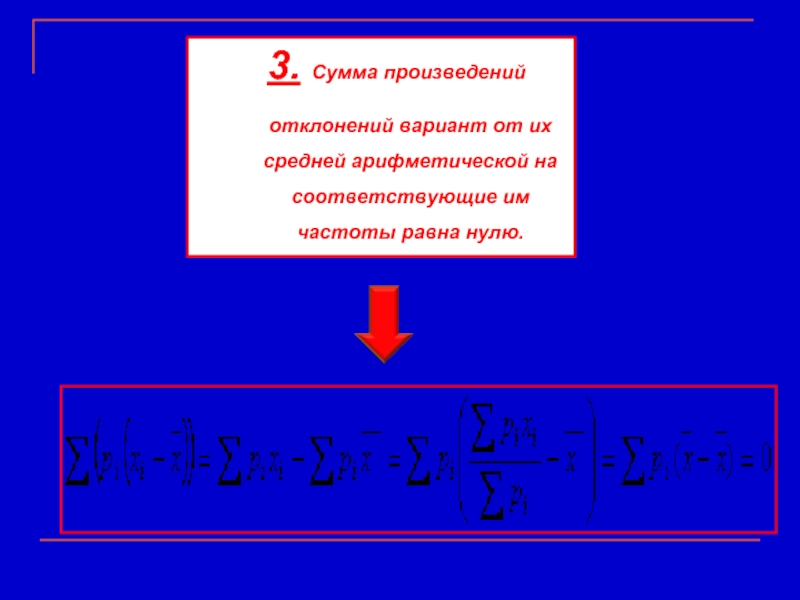
Слайд 93. Сумма произведений отклонений вариант от их средней арифметической на соответствующие
Слайд 10
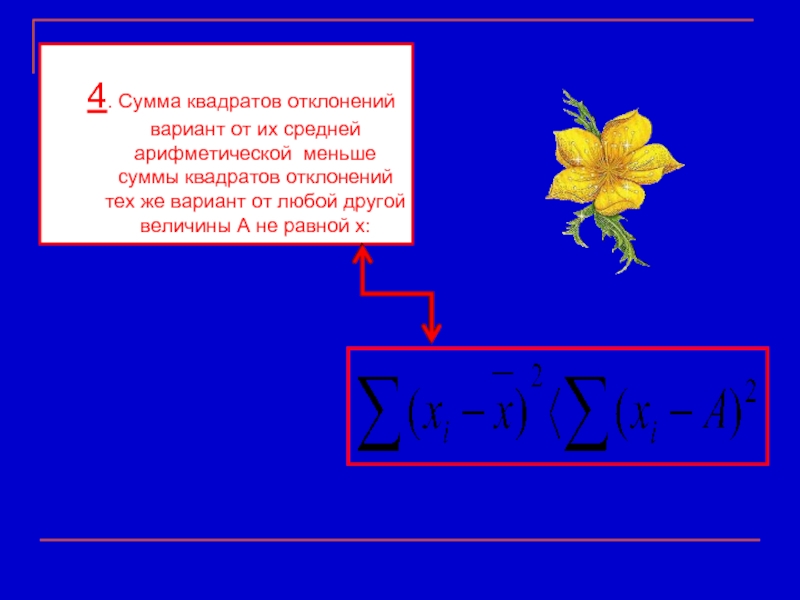
4. Сумма квадратов отклонений вариант от их средней арифметической меньше суммы
Слайд 12Медиана эмпирического распределения (Me) (от лат. Mediana – средняя) – средняя,
Если число членов ранжированного ряда нечетное, то центральная варианта и будет Me.
При четном числе членов ряда медиана определяется по полусумме двух соседних вариант, расположенных в центре ряда.
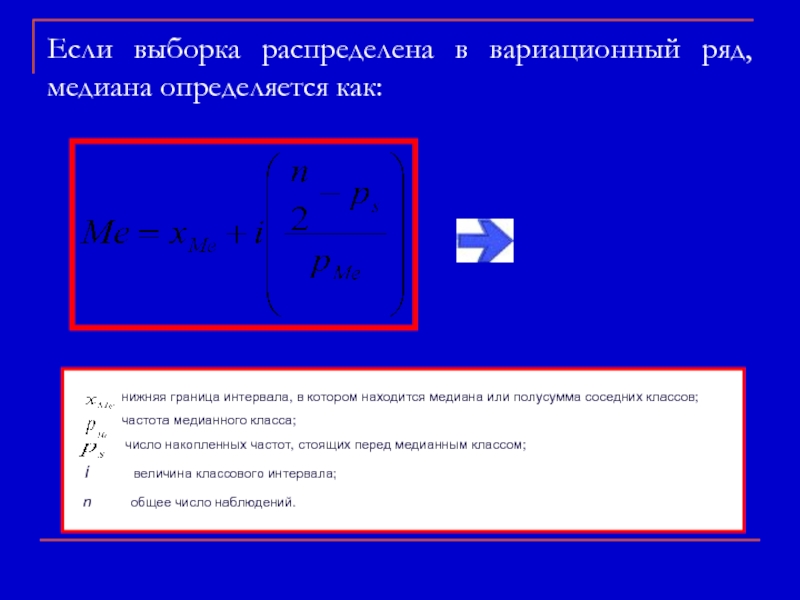
Слайд 13Если выборка распределена в вариационный ряд, медиана определяется как:
нижняя
частота медианного класса;
число накопленных частот, стоящих перед медианным классом;
i величина классового интервала;
n общее число наблюдений.
Слайд 14Мода (Mo) – величина, которая встречается в данной совокупности наиболее часто.
Класс с наибольшей частотой называется модальным.
где:
- нижняя граница модального класса, т.е. класса с
наибольшей частотой ( )
- частота класса, предшествующего модальному,
- частота класса, следующего за модальным,
- ширина классового промежутка.
Слайд 15Квантили - структурные средние характеристики вариационного ряда, отсекающие в пределах вариационного
Слайд 16Квартиль – величина, отсекающая 1/4
(3 квартиля делят весь вариационный ряд на четыре равночисленные части (кварты)).
Дециль – величина, отделяющая 1/10 часть всех членов вариационного ряда.
(9 децилей делят весь вариационный ряд на десять равных частей).
Перцентиль (процентиль) отсекает сотые доли вариант.
(99 децилей делят совокупность на 100 равных частей).
Слайд 18Лимиты (от лат limes - предел) – значения максимальной и минимальной
Слайд 20Дисперсия (от лат. Dispersion - рассеяние) или варианса (англ. Variance -
Дисперсия генеральной совокупности - σ², дисперсия выборки - S² .
Слайд 21Знак суммирования произведений отклонений вариант xi от их средней
Частоты
Объем
Число степеней свободы
Число степеней свободы - число свободно варьирующих единиц или элементов в составе данной ограниченной совокупности.
Слайд 22Свойства дисперсии:
1. Если каждую варианту совокупности увеличить или уменьшить на одно
Т.о. дисперсию можно вычислить не только по значениям признака, но и по их отклонениям от какой-нибудь постоянной величины А.
Слайд 232. Если каждую варианту разделить или умножить на одно и то
Слайд 24Среднее квадратическое отклонение (Sx)
Характеризует величину и специфику варьирования признака.
Среднее квадратическое отклонение
Cтандартное отклонение (standard deviation – англ.)
Чем сильнее варьирует признак, тем больше среднее квадратическое отклонение.
Дисперсия и среднее квадратическое отклонение выражаются в тех же единицах, что и характеризуемый признак.
Слайд 25Показатель, предложенный К. Пирсеном –обозначаемый буквой V (или CV) называется коэффициентом
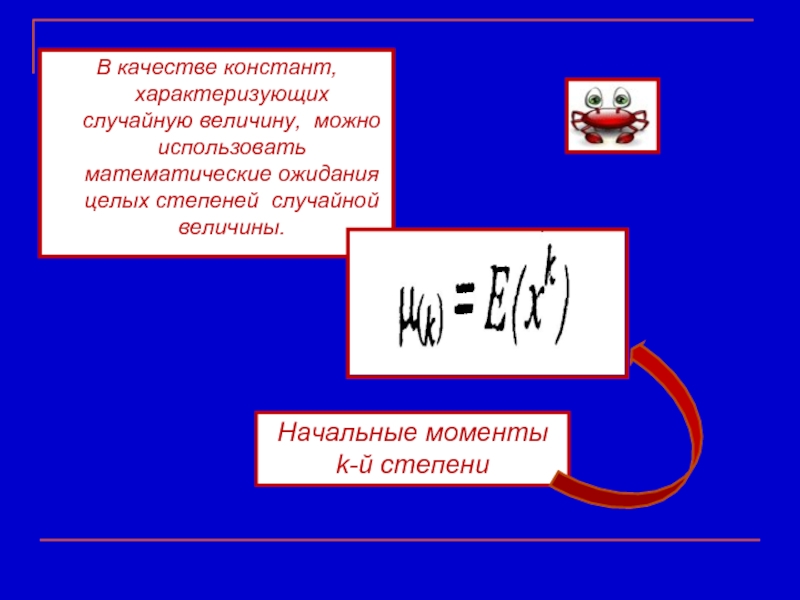
Слайд 26В качестве констант, характеризующих случайную величину, можно использовать математические ожидания целых
Начальные моменты k-й степени
Слайд 27Проверка нормальности распределения с помощью показателей асимметрии и эксцесса
Выборочные характеристики
Многие биологические признаки распределяются нормально. Нередко, однако, эмпирические ряды распределения отклоняются более или менее заметно от нормальной кривой. Эти отклонения могут быть различными, обнаруживая в одних случаях асимметрию, в других — эксцесс, а иногда и то и другое одновременно.
Слайд 28Асимметрия или коэффициент асимметрии (термин был впервые введен Пирсоном, 1895) является
Где:
μ3 - равно ∑(xi- среднееx)3
σ3 - стандартное отклонение (сигма), возведенное в
третью степень;
n - число наблюдений.
Слайд 29Асимметрия или коэффициент асимметрии (термин был впервые введен Пирсоном, 1895) является
Где:
μ3 - равно ∑(xi- среднееx)3
σ3 - стандартное отклонение (сигма), возведенное в
третью степень;
n - число наблюдений.
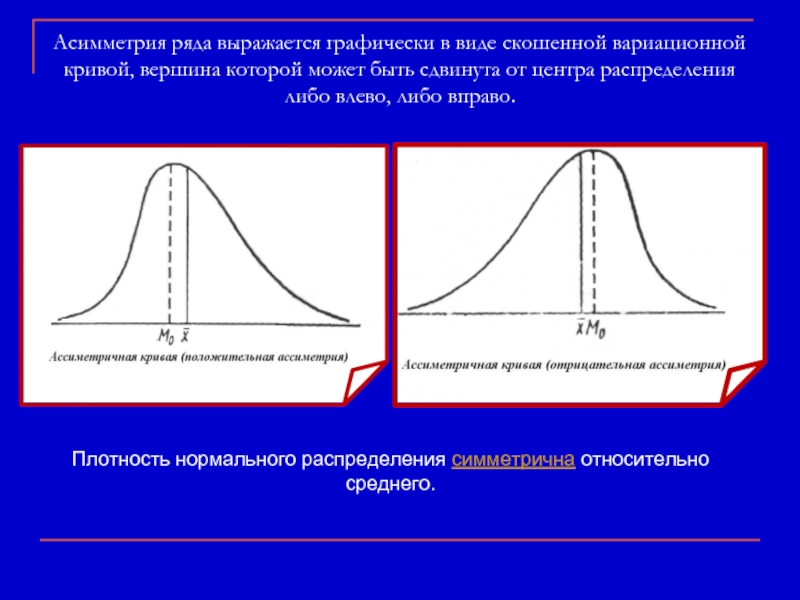
Слайд 31Асимметрия ряда выражается графически в виде скошенной вариационной кривой, вершина которой
Плотность нормального распределения симметрична относительно среднего.
Слайд 32Коэффициент ассиметрии – величина безразмерная, может принимать значения от -∞ до
При симметричном распределении μ(3)=0 и α=0.
Слайд 33Асимметрию называют правосторонней или положительной, если вершина кривой сдвинута влево от
При левосторонней, или отрицательной, асимметрии, наоборот, вершина кривой сдвинута вправо от центра распределения, а ее пологая часть находится на левой стороне.
Слайд 34Эксцесс
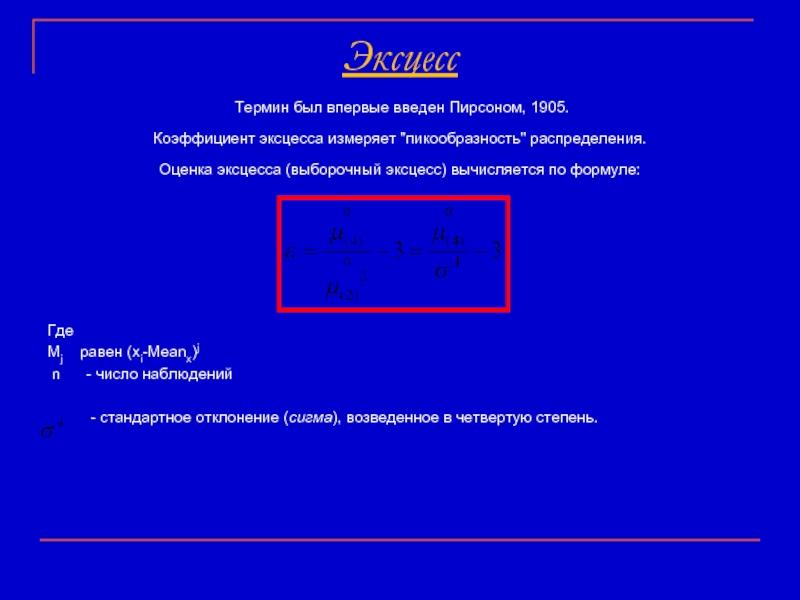
Термин был впервые введен Пирсоном, 1905.
Коэффициент эксцесса измеряет "пикообразность" распределения.
Оценка эксцесса (выборочный эксцесс) вычисляется по формуле:
Где
Mj равен (xi-Meanx)j
n - число наблюдений
- стандартное отклонение (сигма), возведенное в четвертую степень.
Слайд 35Эксцесс
Термин был впервые введен Пирсоном, 1905.
Коэффициент эксцесса измеряет "пикообразность" распределения.
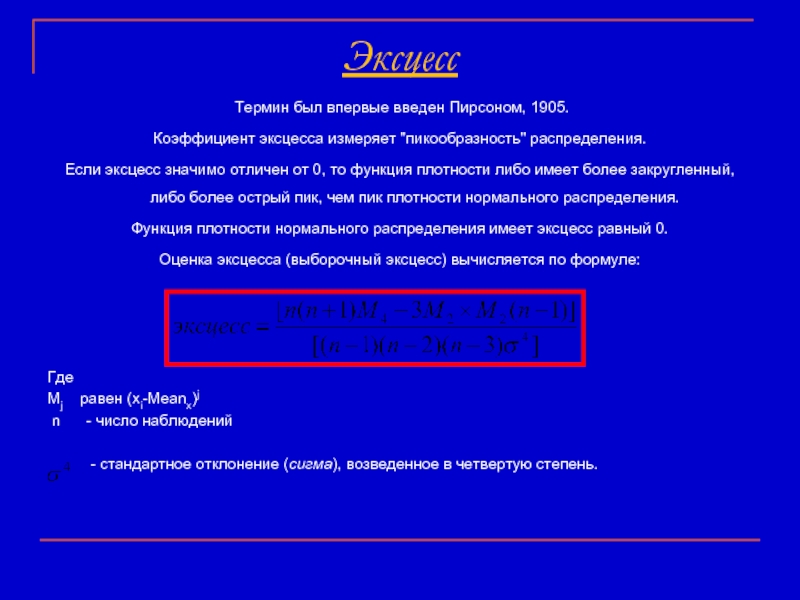
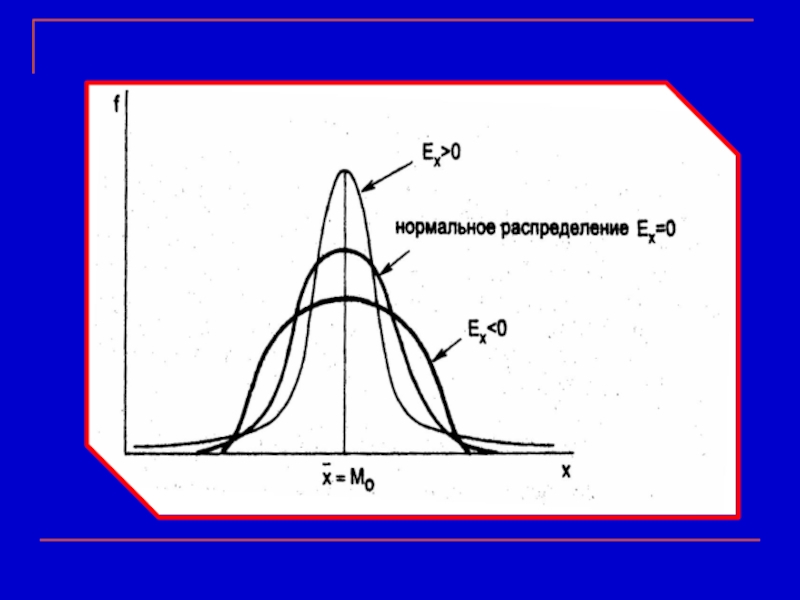
Если эксцесс значимо отличен от 0, то функция плотности либо имеет более закругленный, либо более острый пик, чем пик плотности нормального распределения.
Функция плотности нормального распределения имеет эксцесс равный 0.
Оценка эксцесса (выборочный эксцесс) вычисляется по формуле:
Где
Mj равен (xi-Meanx)j
n - число наблюдений
- стандартное отклонение (сигма), возведенное в четвертую степень.
Слайд 37Если эксцесс значимо отличен от 0, то функция плотности либо имеет
Функция плотности нормального распределения имеет эксцесс равный 0.