- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Обработка результатов эксперимента в MathCad презентация
Содержание
- 1. Обработка результатов эксперимента в MathCad
- 2. 1. Законы распределения случайных чисел Распределение случайной
- 3. Законы распределения случайных чисел Для непрерывных случайных
- 4. Равномерное распределение 2 параметра: a,
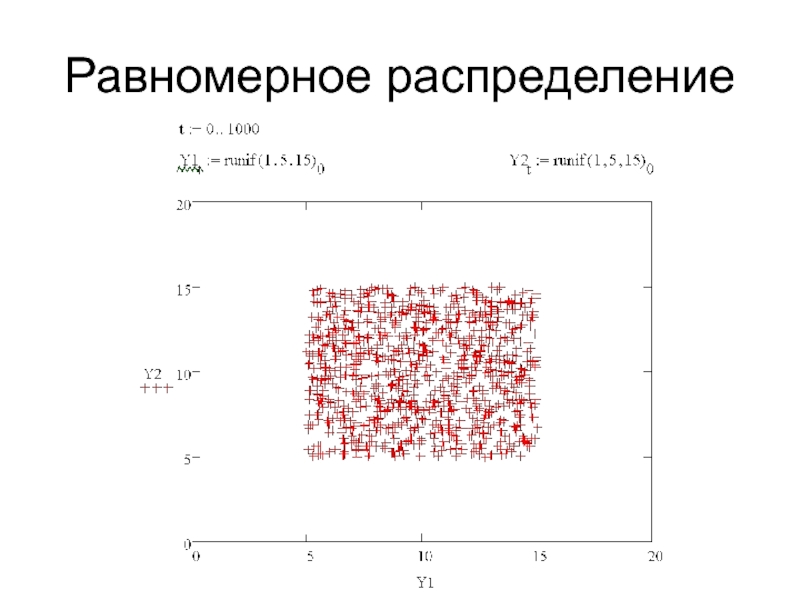
- 5. Равномерное распределение
- 6. Нормальное распределение 2 параметра: μ – мат. ожидание σ – стандартное, или среднеквадратическое, отклонение
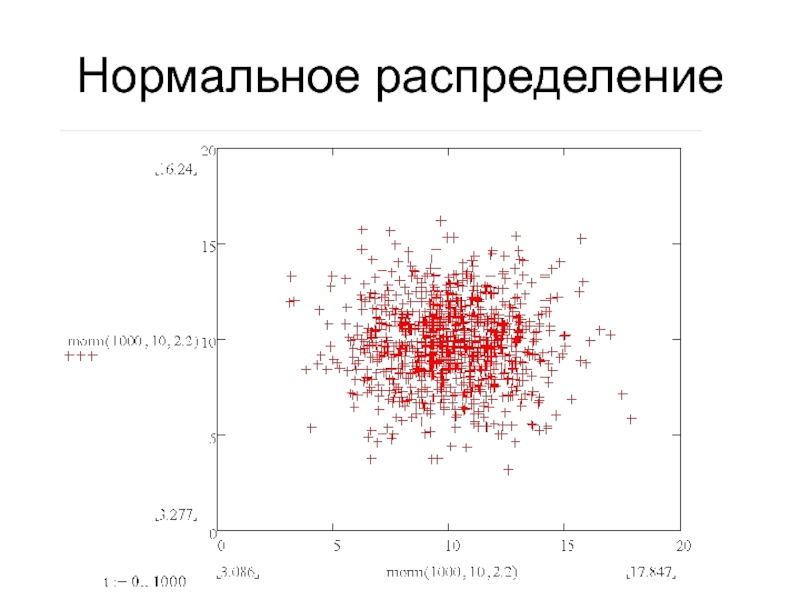
- 7. Нормальное распределение
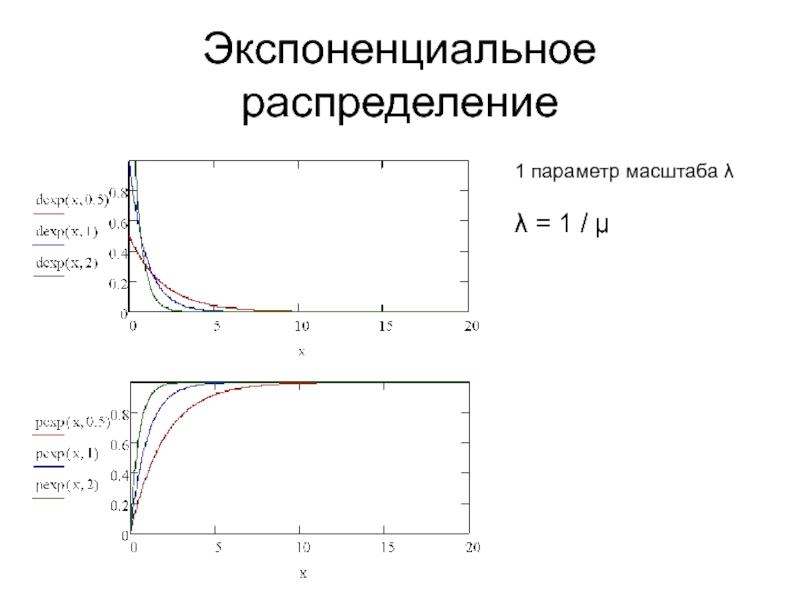
- 8. Экспоненциальное распределение 1 параметр масштаба λ λ = 1 / μ
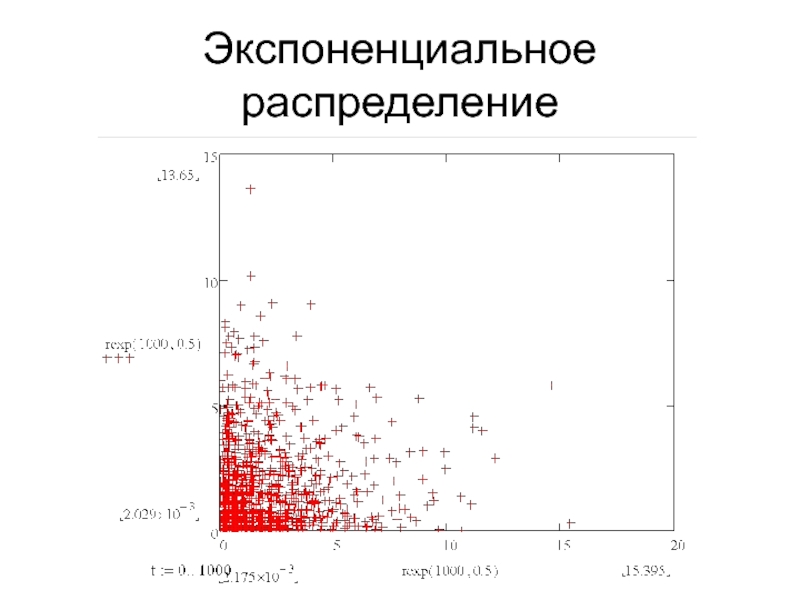
- 9. Экспоненциальное распределение
- 10. Гамма-распределение 2 параметра: k – параметр формы
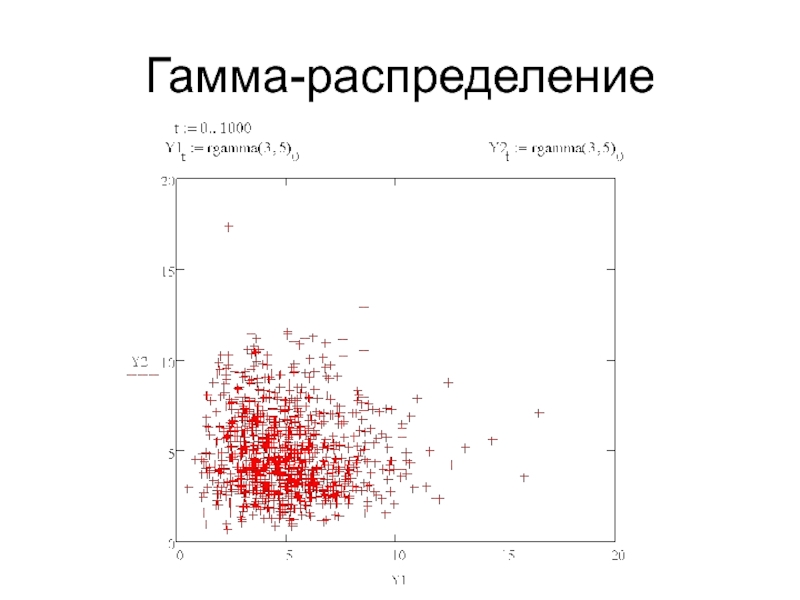
- 11. Гамма-распределение
- 12. 2. Построение гистограмм плотности вероятности
- 13. Построение гистограмм плотности вероятности и интегральной функции распределения Построение гистограммы плотности вероятности:
- 14. Построение гистограмм плотности вероятности и
- 15. Построение гистограмм плотности вероятности и интегральной функции распределения Построение гистограммы интегральной функции распределения:
- 16. 4. Вычисление математического ожидания, стандартного отклонения, дисперсии
- 17. 5. Критерии достоверности гипотез Гипотеза – предположение
- 18. Критерии достоверности гипотез Для проверки гипотез вычисляют
- 19. Использование критерия Колмогорова Упорядочить случайные числа по
- 20. Использование критерия Колмогорова при заданном уровне
- 21. Поиск критической точки для критерия Колмогорова Для
- 22. Критерий Колмогорова: пример Пассажир, приходящий в случайные
- 23. Решение
- 24. Решение задачи в MathCAD
- 25. Использование критерия Пирсона Критерий используется для дискретных
- 26. Использование критерия Пирсона Определить число степеней свободы
- 27. Использование критерия Пирсона Вычисление χ2:
- 28. Пример Измерены интервалы в минутах между 100
- 29. Неравенство χ2 < χ2кр выполнено, гипотезу можно принять.
- 30. 6. Коэффициент линейной корреляции Коэффициент линейной
- 31. Задание к работе 6 Сгенерировать случайные числа
Слайд 21. Законы распределения случайных чисел
Распределение случайной величины – это функция, позволяющая
определить вероятность появления заданного значения случайной величины.
В теории вероятностей сформулировано несколько законов распределения как для дискретных, так и для непрерывных случайных величин.
Наблюдаемые на практике случайные величины часто не вполне соответствуют теоретическим распределениям, но с некоторой точностью могут быть приближенно ими представлены.
В теории вероятностей сформулировано несколько законов распределения как для дискретных, так и для непрерывных случайных величин.
Наблюдаемые на практике случайные величины часто не вполне соответствуют теоретическим распределениям, но с некоторой точностью могут быть приближенно ими представлены.
Слайд 3Законы распределения случайных чисел
Для непрерывных случайных величин рассмотрим следующие законы:
Равномерное распределение
Нормальное
распределение
Экспоненциальное распределение
Гамма-распределение
Экспоненциальное распределение
Гамма-распределение
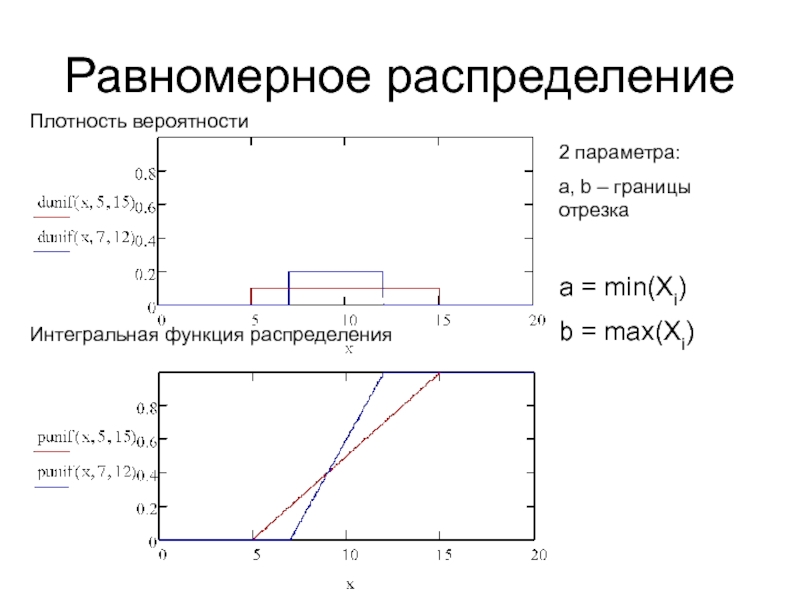
Слайд 4Равномерное распределение
2 параметра:
a, b – границы отрезка
a = min(Xi)
b =
max(Xi)
Плотность вероятности
Интегральная функция распределения
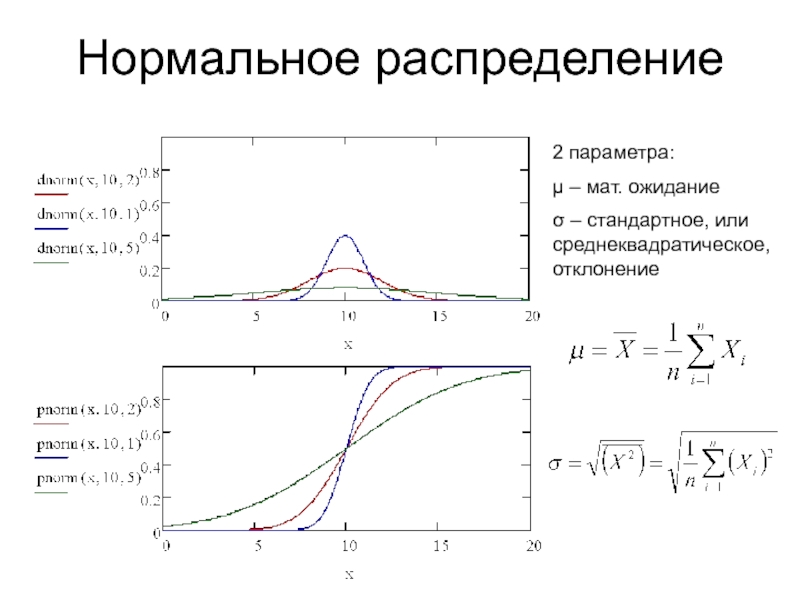
Слайд 6Нормальное распределение
2 параметра:
μ – мат. ожидание
σ – стандартное, или среднеквадратическое,
отклонение
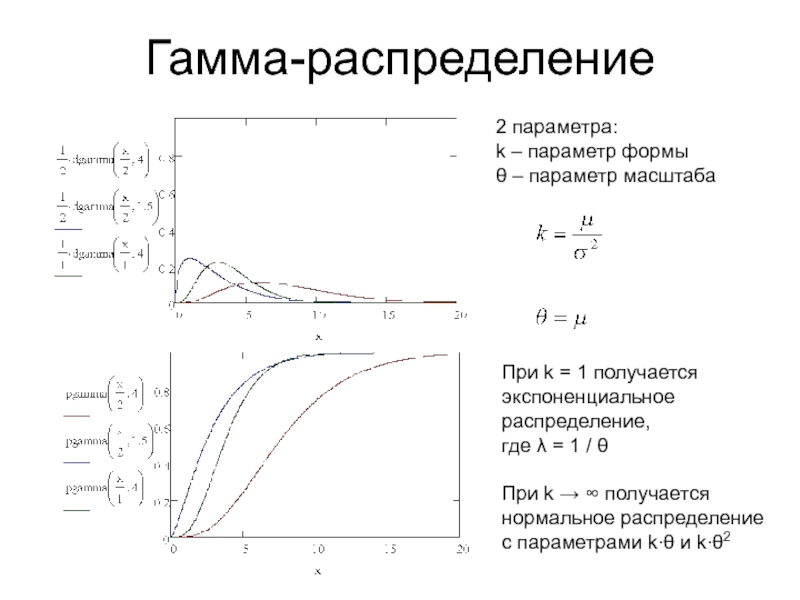
Слайд 10Гамма-распределение
2 параметра:
k – параметр формы
θ – параметр масштаба
При k = 1
получается экспоненциальное распределение,
где λ = 1 / θ
При k → ∞ получается нормальное распределение с параметрами k∙θ и k∙θ2
где λ = 1 / θ
При k → ∞ получается нормальное распределение с параметрами k∙θ и k∙θ2
Слайд 122. Построение гистограмм
плотности вероятности
и интегральной функции распределения
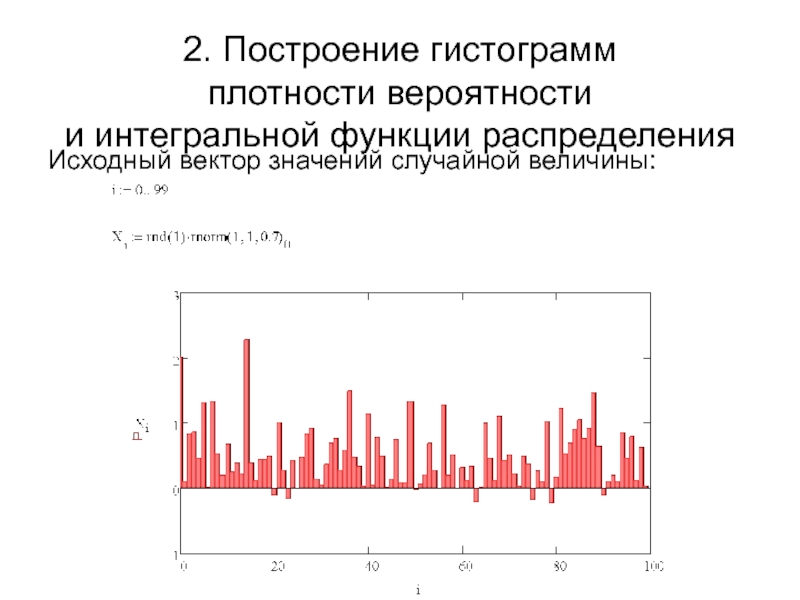
Исходный вектор значений
случайной величины:
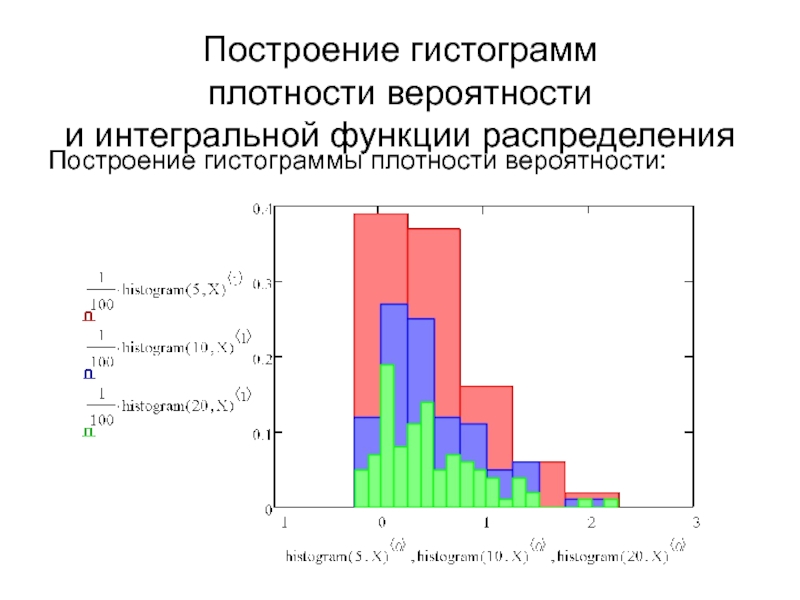
Слайд 13Построение гистограмм
плотности вероятности
и интегральной функции распределения
Построение гистограммы плотности вероятности:
Слайд 14Построение гистограмм
плотности вероятности
и интегральной функции распределения
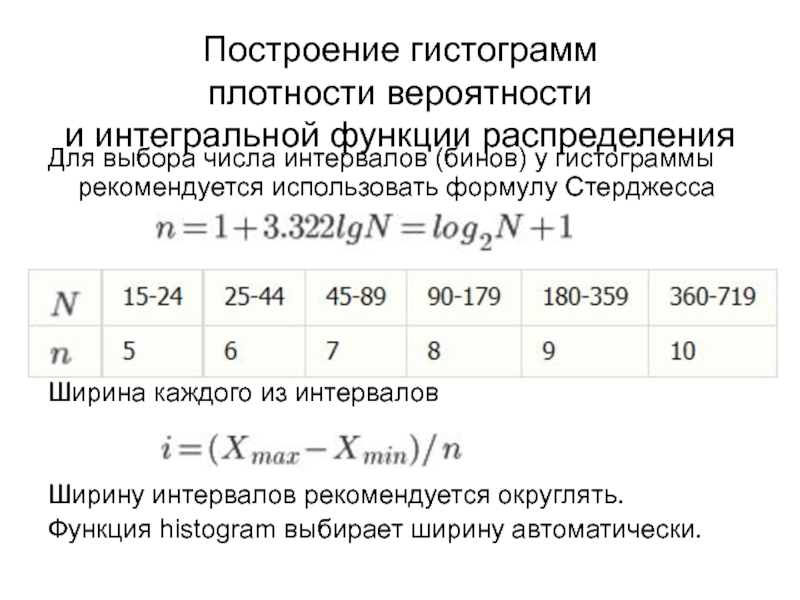
Для выбора числа интервалов
(бинов) у гистограммы рекомендуется использовать формулу Стерджесса
Ширина каждого из интервалов
Ширину интервалов рекомендуется округлять.
Функция histogram выбирает ширину автоматически.
Ширина каждого из интервалов
Ширину интервалов рекомендуется округлять.
Функция histogram выбирает ширину автоматически.
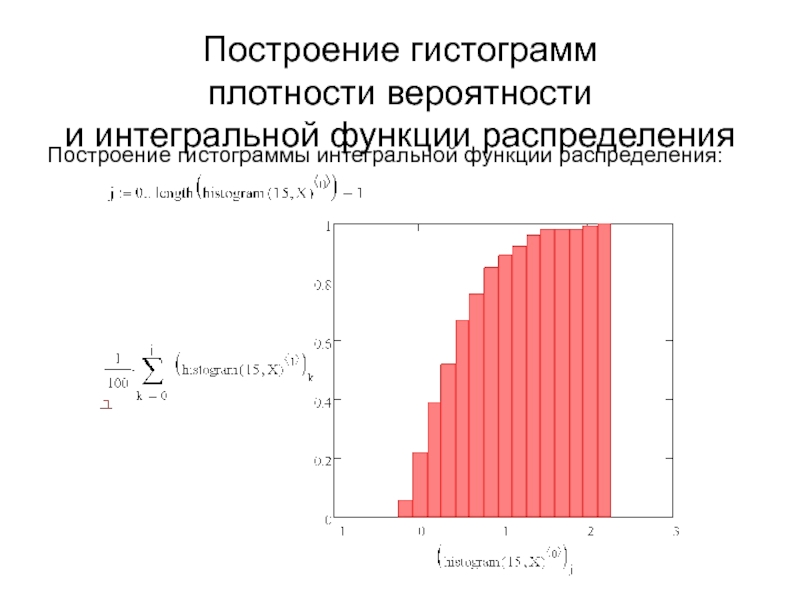
Слайд 15Построение гистограмм
плотности вероятности
и интегральной функции распределения
Построение гистограммы интегральной функции
распределения:
Слайд 164. Вычисление математического ожидания, стандартного отклонения, дисперсии
Математическое ожидание случайной величины
вычисляется как её среднее значение, в mathCad вычисляется функцией mean
Среднеквадратическое (стандартное) отклонение – корень из дисперсии, в mathCad вычисляется функцией stdev Обозначается σ
Дисперсия – среднее значение квадрата отклонений от среднего значения (σ2), в mathCad вычисляется функцией var
Среднеквадратическое (стандартное) отклонение – корень из дисперсии, в mathCad вычисляется функцией stdev Обозначается σ
Дисперсия – среднее значение квадрата отклонений от среднего значения (σ2), в mathCad вычисляется функцией var
Слайд 175. Критерии достоверности гипотез
Гипотеза – предположение о виде или параметрах неизвестного
распределения.
Например: гипотеза «случайная величина X подчиняется нормальному закону распределения»
Для каждой гипотезы есть вероятность p, что она верна, и вероятность 1 – p, что гипотеза ошибочна.
При проверке гипотез заранее задают уровень значимости α = 1 – p, то есть вероятность недостоверности гипотезы.
Например: гипотеза «случайная величина X подчиняется нормальному закону распределения»
Для каждой гипотезы есть вероятность p, что она верна, и вероятность 1 – p, что гипотеза ошибочна.
При проверке гипотез заранее задают уровень значимости α = 1 – p, то есть вероятность недостоверности гипотезы.
Слайд 18Критерии достоверности гипотез
Для проверки гипотез вычисляют значение критерия, зависящее от значений
проверяемой случайной величины, и проверяют его на нахождение в области значений, соответствующей достоверности гипотезы при заданном уровне значимости.
Наиболее часто используют критерий Колмогорова и критерий Пирсона (критерий «хи-квадрат» - χ2 ).
Наиболее часто используют критерий Колмогорова и критерий Пирсона (критерий «хи-квадрат» - χ2 ).
Слайд 19Использование критерия Колмогорова
Упорядочить случайные числа по возрастанию.
Вычислить значения Di и выбрать
максимальное из них D
Значение критерия λ = D √n
Найти вероятность совпадения законов распределения P(λ).
Значение критерия λ = D √n
Найти вероятность совпадения законов распределения P(λ).
Слайд 20Использование критерия Колмогорова
при заданном уровне значимости
Задавшись α и зная n,
выбрать критическое значение критерия Dкр.
Упорядочить случайные числа по возрастанию.
Вычислить значения критерия Di и выбрать максимальное из них D
Гипотезу о принадлежности случайной величины распределению можно принять, если D < Dкр
Упорядочить случайные числа по возрастанию.
Вычислить значения критерия Di и выбрать максимальное из них D
Гипотезу о принадлежности случайной величины распределению можно принять, если D < Dкр
Слайд 21Поиск критической точки для критерия Колмогорова
Для нахождения критической величины критерия Dкр
надо знать уровень значимости α и число опытов n
Для заданного α выбираем λкр:
Для заданного α выбираем λкр:
При больших n
(n > 35)
Для малых n пользоваться табличными значениями Dкр
Слайд 22Критерий Колмогорова: пример
Пассажир, приходящий в случайные моменты времени на автобусную остановку,
в течение пяти поездок фиксировал своё время ожидания автобуса: 5,1; 3,7; 1,2; 9,2; 4,8 мин. Проверить гипотезу о том, что время ожидания автобуса равномерно распределено на отрезке [0; 10] на уровне значимости 0,05.
Слайд 25Использование критерия Пирсона
Критерий используется для дискретных величин, либо непрерывных величин, разбитых
на интервалы.
Например, он может быть использован, если построена гистограмма результатов эксперимента.
Например, он может быть использован, если построена гистограмма результатов эксперимента.
Слайд 26Использование критерия Пирсона
Определить число степеней свободы
k = l – r
– 1, где
l – число интервалов гистограммы
r – число параметров предполагаемого распределения, оцениваемых по выборке
(2 для нормального, 1 для экспоненциального…)
Найти критическое значение критерия:
χ2кр = qchisq(1 – α, k)
Вычислить критерий χ2 по экспериментальным данным. Гипотеза верна, если
χ2 < χ2кр
Найти критическое значение критерия:
χ2кр = qchisq(1 – α, k)
Вычислить критерий χ2 по экспериментальным данным. Гипотеза верна, если
χ2 < χ2кр
Слайд 27Использование критерия Пирсона
Вычисление χ2:
где
ni – эмпирические частоты (фактическое количество попаданий случайной
величины в заданный интервал гистограммы)
npi – теоретические частоты (количество попаданий случайной величины в заданный интервал гистограммы, вычисленное по предполагаемому закону её распределения)
npi – теоретические частоты (количество попаданий случайной величины в заданный интервал гистограммы, вычисленное по предполагаемому закону её распределения)
Слайд 28Пример
Измерены интервалы в минутах между 100 поездами метро, прибывшими на станцию.
Результаты измерений представлены статистическим рядом:
На уровне значимости проверить гипотезу о том, что интервалы можно описать нормальным распределением.
На уровне значимости проверить гипотезу о том, что интервалы можно описать нормальным распределением.
Слайд 306. Коэффициент
линейной корреляции
Коэффициент линейной корреляции – величина, показывающая наличие линейной
связи между значениями двух случайных величин.
Для линейно зависящих величин он равен 1 или -1, для независимых величин – 0.
В MathCad вычисляется как функция от двух векторов случайных чисел.
Для линейно зависящих величин он равен 1 или -1, для независимых величин – 0.
В MathCad вычисляется как функция от двух векторов случайных чисел.
Слайд 31Задание к работе 6
Сгенерировать случайные числа по своему варианту два раза,
векторы по 50 и 500 шт.
Найти мат. ожидание, стандартное отклонение, дисперсию для обоих наборов случайных чисел
Определить параметры распределения случайной величины, предполагая, что она распределена по известному закону распределения, для каждого из рассмотренных законов.
Построить гистограммы плотности вероятности и интегральной функции распределения. Построить функции плотности вероятности и интегральных функций распределения с найденными параметрами на тех же графиках.
Найти вероятности достоверности гипотез о принадлежности случайной величины к каждому из 4 распределений из п. 4 по критерию Колмогорова. Проверить те же гипотезы по критерию Пирсона для уровня значимости 0,1.
Найти коэффициент корреляции между 1 вектором и первыми 50 числами второго вектора.
Найти мат. ожидание, стандартное отклонение, дисперсию для обоих наборов случайных чисел
Определить параметры распределения случайной величины, предполагая, что она распределена по известному закону распределения, для каждого из рассмотренных законов.
Построить гистограммы плотности вероятности и интегральной функции распределения. Построить функции плотности вероятности и интегральных функций распределения с найденными параметрами на тех же графиках.
Найти вероятности достоверности гипотез о принадлежности случайной величины к каждому из 4 распределений из п. 4 по критерию Колмогорова. Проверить те же гипотезы по критерию Пирсона для уровня значимости 0,1.
Найти коэффициент корреляции между 1 вектором и первыми 50 числами второго вектора.