- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Свойства функции презентация
Содержание
- 1. Свойства функции
- 2. План Возрастание и убывание функции Ограниченность
- 3. Определение № 1 Функцию у= f(x)
- 4. Возрастающая функция Функция возрастает, если большему
- 5. Определение № 2 Функцию у= f(x)
- 6. Убывающая функция Функция убывает,
- 7. Обычно термины «возрастающая функция», «убывающая функция» объединяют
- 8. Определение № 3 Функцию у= f(x)
- 9. Определение № 4 Функцию у=
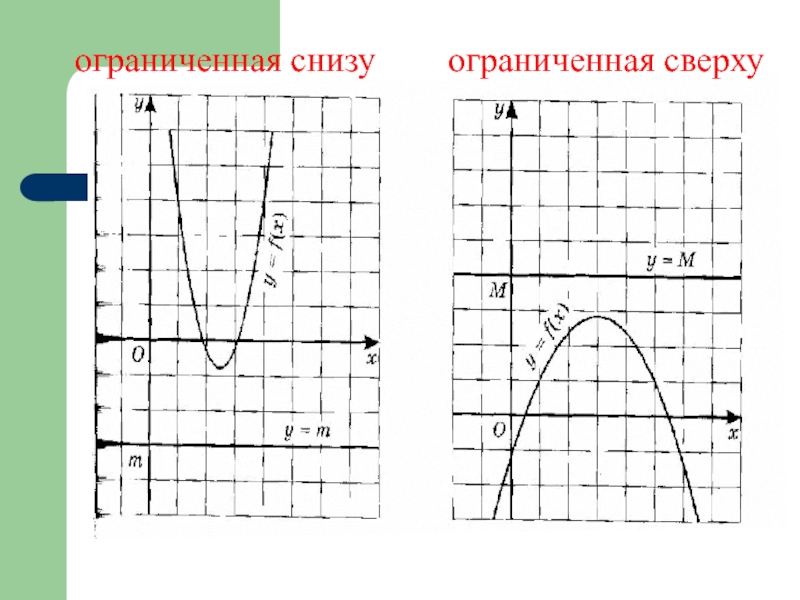
- 10. ограниченная сверху ограниченная снизу
- 11. Если функция ограничена и снизу
- 12. Определение № 5 Число m называют
- 13. Определение № 6 Число М называют
- 14. Утверждения: Если у функции существует yнаиб,
- 15. Определение № 7 Точку x0 называют
- 16. Определение № 8 Точку x0 называют точкой
- 17. а) Укажите точки экстремума и определите их вид; б) укажите наибольшее и наименьшее значение функции.
- 18. Выпуклость функции Функция выпукла вниз на промежутке
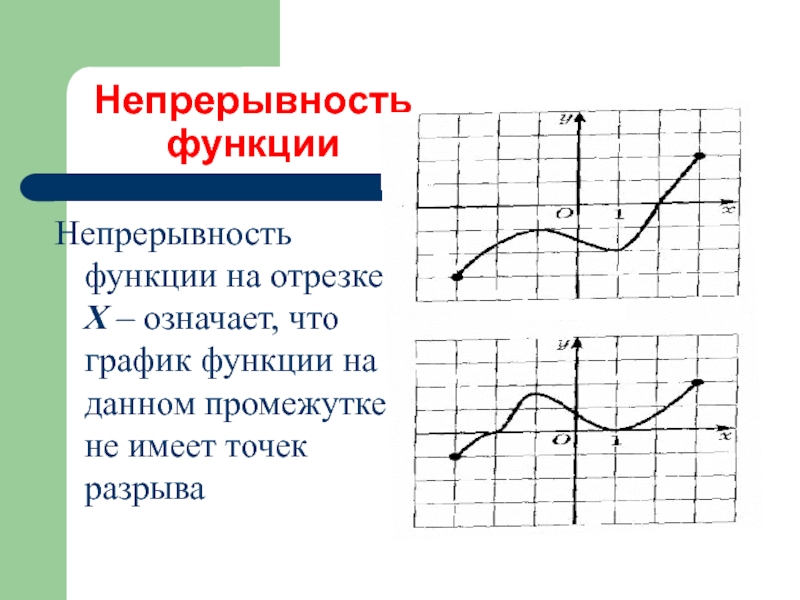
- 20. Непрерывность функции Непрерывность функции на
- 22. Определение 11 Функцию у= f(x) называют четной,
- 23. Определение 12 Функцию у= f(x) называют нечетной,
- 25. Утверждения: Если график функции симметричен относительно оси
- 26. Алгоритм исследования функции 1. Область определения
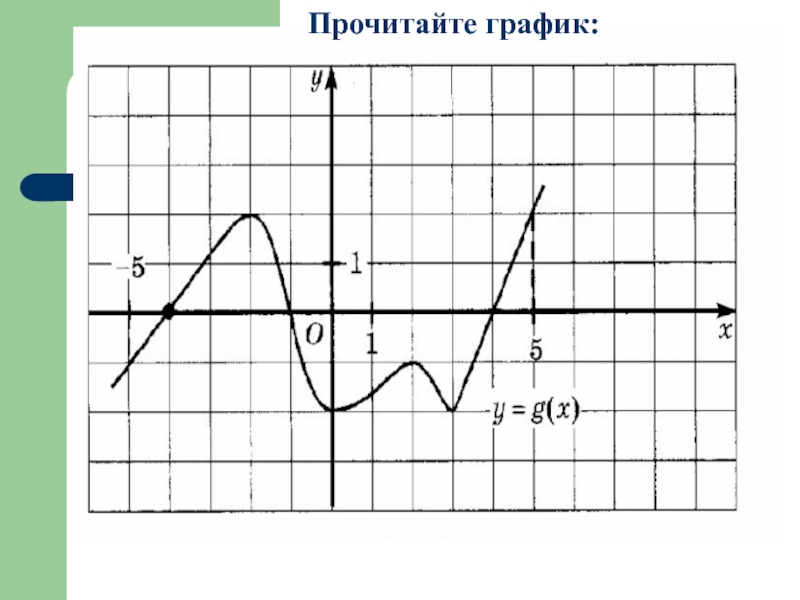
- 27. Прочитайте график:
План Возрастание и убывание функции Ограниченность функции Наибольшее и наименьшее значения функции Максимум и минимум функции Четность и нечетность
Слайд 2План
Возрастание и убывание функции
Ограниченность функции
Наибольшее и наименьшее значения функции
Максимум и
минимум функции
Четность и нечетность
Четность и нечетность
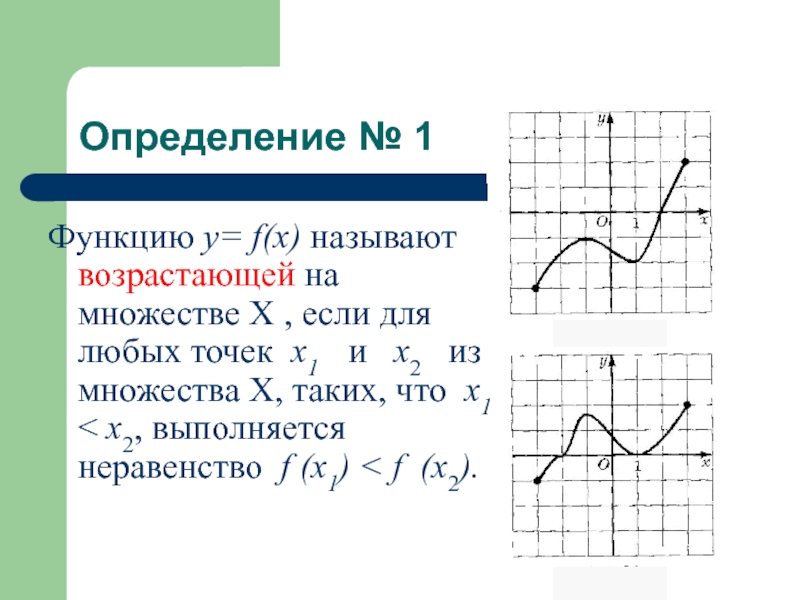
Слайд 3Определение № 1
Функцию у= f(x) называют возрастающей на множестве Х
, если для любых точек x1 и x2 из множества Х, таких, что x1 < x2, выполняется неравенство f (x1) < f (x2).
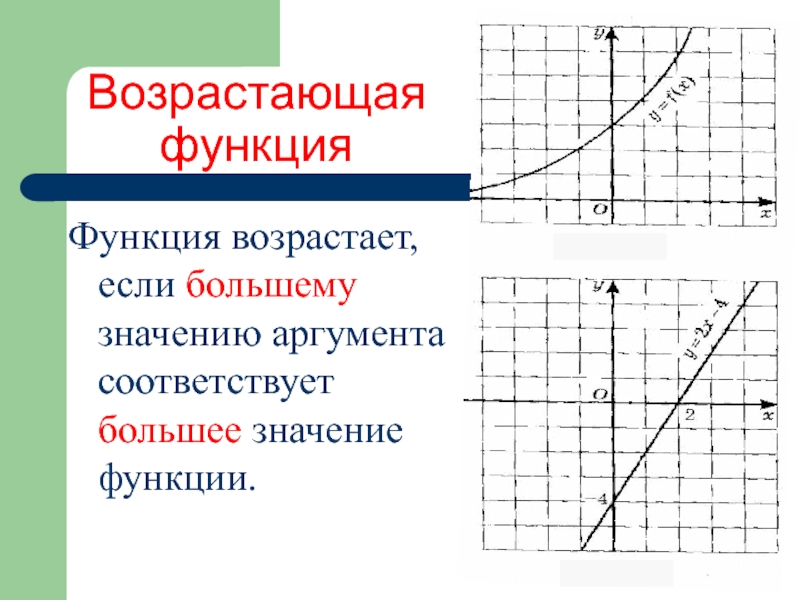
Слайд 4Возрастающая функция
Функция возрастает, если большему значению аргумента соответствует большее значение
функции.
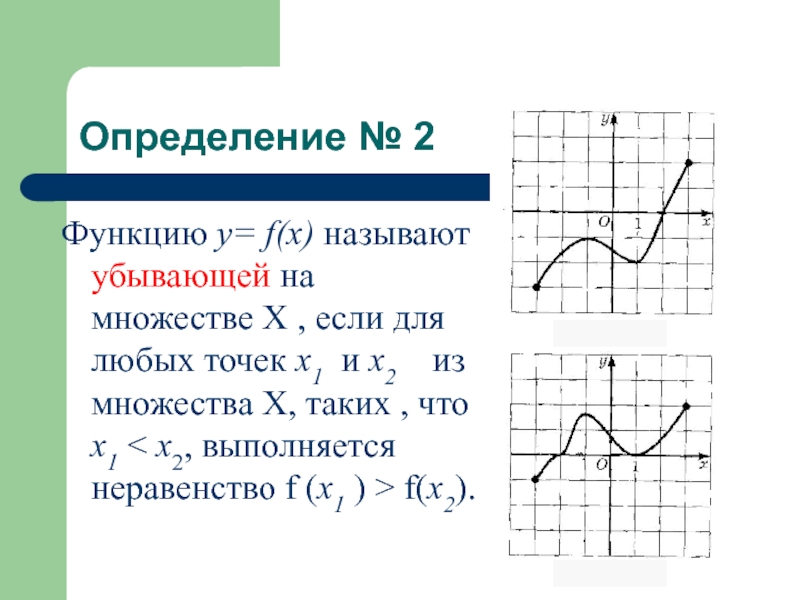
Слайд 5Определение № 2
Функцию у= f(x) называют убывающей на множестве Х
, если для любых точек x1 и x2 из множества Х, таких , что x1 < x2, выполняется неравенство f (x1 ) > f(x2).
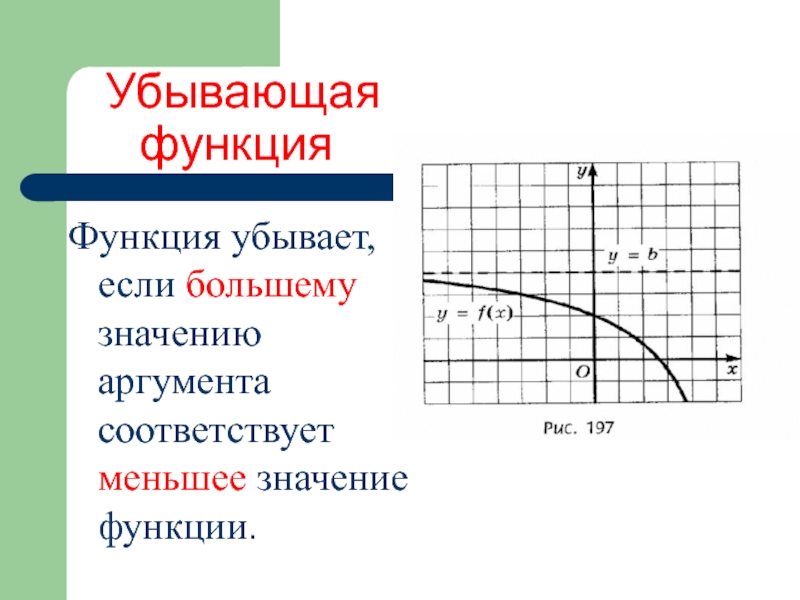
Слайд 6 Убывающая
функция
Функция убывает, если большему значению аргумента соответствует меньшее
значение функции.
Слайд 7Обычно термины «возрастающая функция», «убывающая функция» объединяют общим названием монотонная функция,
а исследование функции на возрастание или убывание называют исследованием функции на монотонность.
Слайд 8Определение № 3
Функцию у= f(x) называют ограниченной снизу на множестве
Х, если все значения этой функции на множестве Х больше некоторого числа, т.е., если существует такое число m, что для любого значения х выполняется неравенство f(x) > m
Слайд 9 Определение № 4
Функцию у= f(x) называют ограниченной сверху на
множестве Х , если все значения этой функции на множестве Х меньше некоторого числа , т.е. , если существует такое число М , что для любого значения х выполняется неравенство f(x) < М
Слайд 11
Если функция ограничена и снизу и сверху на всей области
определения, то ее называют ограниченной
Слайд 12Определение № 5
Число m называют наименьшим значением функции у= f(x)
на множестве Х , если:
1)во множестве Х существует такая точка x0 , что f(x0) = m
2) для любого значения х из множества Х выполняется неравенство
1)во множестве Х существует такая точка x0 , что f(x0) = m
2) для любого значения х из множества Х выполняется неравенство
Слайд 13Определение № 6
Число М называют набольшим значением функции у= f(x)
на множестве Х, если:
1)во множестве Х существует такая точка, что f(x0) = М
2) для любого значения х из множества Х выполняется неравенство
1)во множестве Х существует такая точка, что f(x0) = М
2) для любого значения х из множества Х выполняется неравенство
Слайд 14Утверждения:
Если у функции существует yнаиб,
то она ограничена сверху
Если у
функции существует yнаим, то она ограничена снизу.
Слайд 15Определение № 7
Точку x0 называют точкой максимума функции у= f(x),
если у этой точки существует окрестность, для всех точек которой (кроме самой точки x0) выполняется неравенство
Слайд 16Определение № 8
Точку x0 называют точкой минимума функции у= f(x), если
у этой точки существует окрестность, для всех точек которой ( кроме самой точки x0) выполняется неравенство
Точки максимума и минимума объединяют общим названием – точки экстремума
Точки максимума и минимума объединяют общим названием – точки экстремума
Слайд 17а) Укажите точки экстремума и определите их вид;
б) укажите наибольшее и
наименьшее значение функции.
Слайд 18Выпуклость функции
Функция выпукла вниз на промежутке Х, если, соединив любые две
точки ее графика (с абсциссами из Х) отрезком, мы обнаружим, что соответствующая часть графика лежит ниже проведенного отрезка.
Функция выпукла вверх на промежутке Х, если, соединив любые две точки ее графика (с абсциссами из Х) отрезком, мы обнаружим, что соответствующая часть графика лежит выше проведенного отрезка.
Функция выпукла вверх на промежутке Х, если, соединив любые две точки ее графика (с абсциссами из Х) отрезком, мы обнаружим, что соответствующая часть графика лежит выше проведенного отрезка.
Определение № 9,10
Слайд 20Непрерывность
функции
Непрерывность функции на отрезке Х – означает, что график
функции на данном промежутке не имеет точек разрыва
Слайд 22Определение 11
Функцию у= f(x) называют четной, если для любого значения х
из множества Х выполняется равенство
Слайд 23Определение 12
Функцию у= f(x) называют нечетной, если для любого значения х
из множества Х выполняется равенство
Слайд 25Утверждения:
Если график функции симметричен относительно оси ординат, то функция четная
Если график
функции симметричен относительно начала координат, то функция нечетная
Слайд 26Алгоритм исследования функции
1. Область определения функции
2. Четность , нечетность
3. Непрерывность
4.
Выпуклость
5. Нули функции
6. Промежутки возрастания и убывания
7. Точки экстремума
8. Ограниченность функции
9. Наибольшее и наименьшее значения функции
10. Множество значений функции
5. Нули функции
6. Промежутки возрастания и убывания
7. Точки экстремума
8. Ограниченность функции
9. Наибольшее и наименьшее значения функции
10. Множество значений функции
