- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Обернені тригонометричні функції презентация
Содержание
- 1. Обернені тригонометричні функції
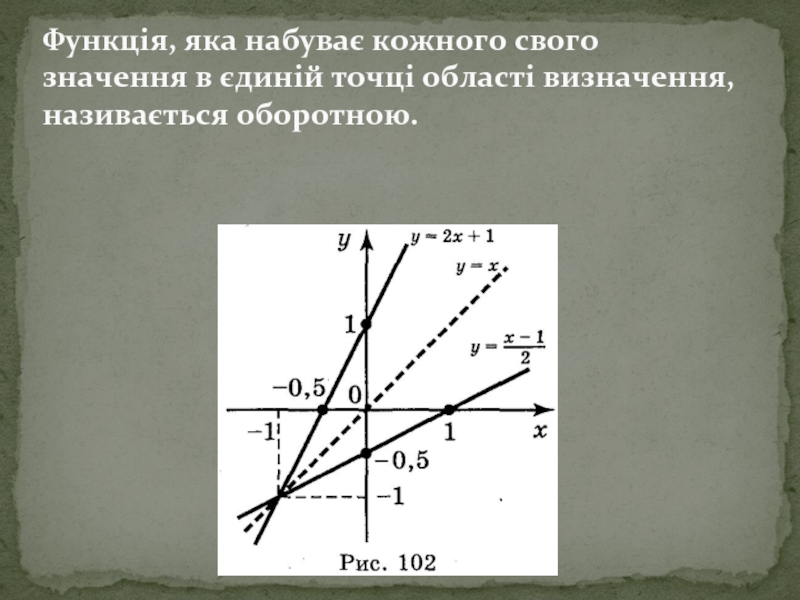
- 2. у = 2х + 1 Щоб
- 3. Функція, яка набуває кожного свого значення в єдиній точці області визначення, називається оборотною.
- 4. Якщо функція у = f(x) задана формулою,
- 5. 1. Які із поданих функцій є оборотними
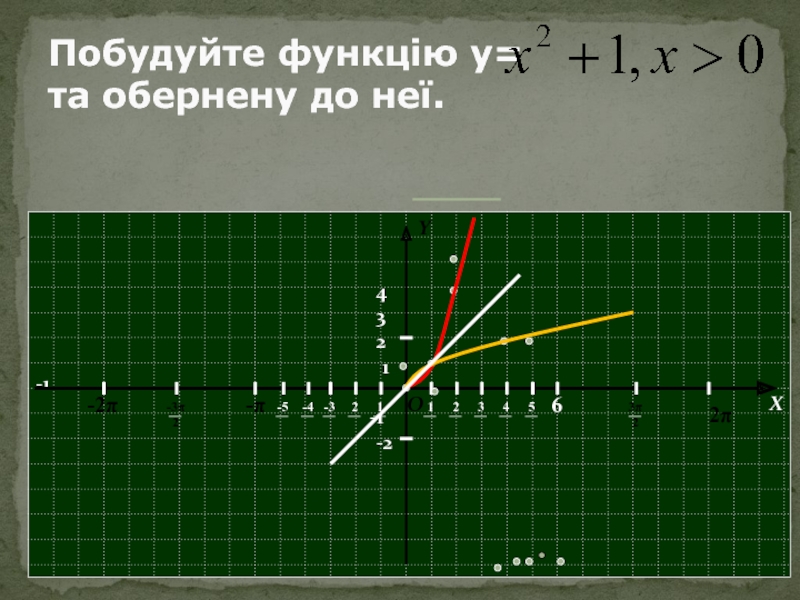
- 6. Побудуйте функцію у= та обернену до неї.
- 7. 1. D(y) = [-1; 1]. 2. Е(у)
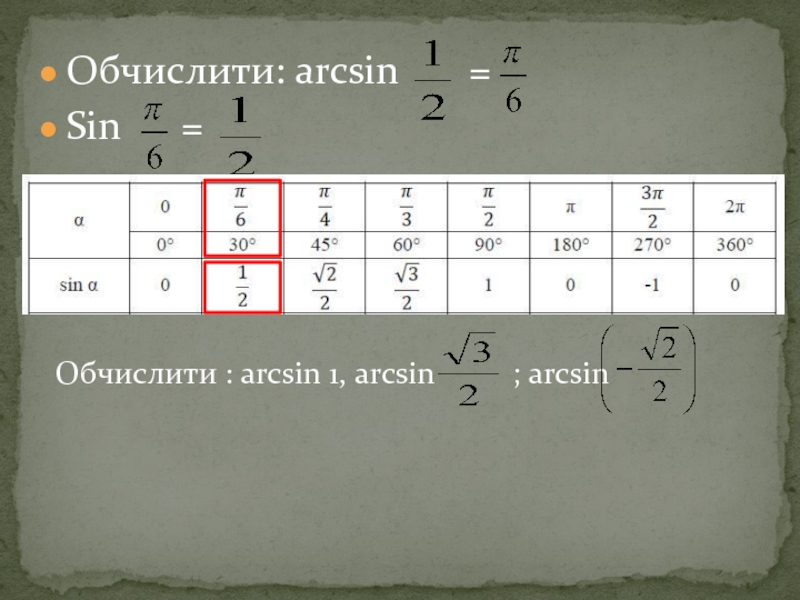
- 8. Обчислити: arcsin = Sin
- 9. 1. D(y) = [-1; 1]. 2. Е(y)=[0;π].
- 10. Обчислити: arcсоs =
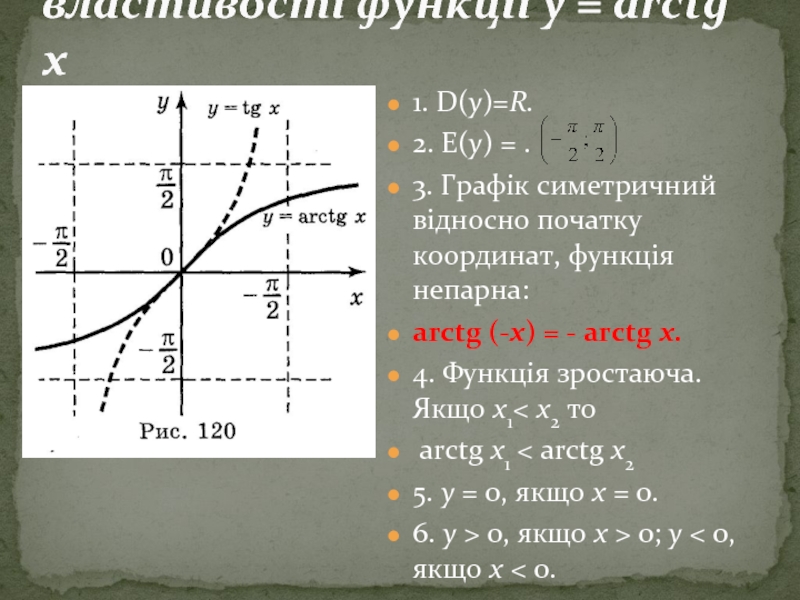
- 11. 1. D(y)=R. 2. Е(у) = . 3.
- 12. 1. D(y)=R. 2. E(y) = (0; π).
- 13. Домашнє завдання. М.І. Шкіль. Розділ
Слайд 2у = 2х + 1
Щоб знайти значення аргументу х, при
2х = у0 – 1 =>
Аргумент цієї функції позначений літерою у, а значення функції — літерою х. Перейшовши до звичних позначень (аргумент — х, функція — у), матимемо функцію:
яка називається оберненою до функції у = 2х + 1.
А функція у = 2х + 1 - оборотна
Слайд 3Функція, яка набуває кожного свого значення в єдиній точці області визначення,
Слайд 4Якщо функція у = f(x) задана формулою, то для знаходження оберненої
Графіки даної функції і оберненої до даної симетричні відносно прямої у = х.
Якщо функція у = f(x) зростає (спадає) на деякому проміжку, то вона оборотна. Обернена функція до даної, визначена області значень функції у = f(x), також є зростаючою (спадною).
Слайд 51. Які із поданих функцій є оборотними в області визначення:
а) у
г)
2. Знайдіть функцію, обернену до даної:
а) у = х - 3; б) ; в) ;
г) у = x2, де х (-∞ ; 0].
Слайд 71. D(y) = [-1; 1].
2. Е(у) = .
3. Графік симетричний відносно
arcsin (-х) = -arcsin х.
4. Функція зростаюча. Якщо х1 > х2 то
arcsin х1 > arcsin х2
5. у = 0, якщо х = 0.
6. уmах = y(1) = , ymіn = y(-1) = - .
Властивості функції у= arcsin х.
Слайд 91. D(y) = [-1; 1].
2. Е(y)=[0;π].
3. Графік не симетричний ні відносно
arccos (-х) = π - arccos х.
4. Функція спадна. Якщо х1 > х2
то arccos х1 < arccos х2.
5. у = 0, якщо х = 1.
6. уmах = y(-1) = π,
ymіn = y(1) = 0.
властивості функції у = arccos х.
Слайд 10Обчислити: arcсоs =
сos =
Обчислити :
arccos
arccos (-х) = π - arccos х.
Слайд 111. D(y)=R.
2. Е(у) = .
3. Графік симетричний відносно початку координат, функція
arctg (-х) = - arctg х.
4. Функція зростаюча. Якщо х1< х2 то
arctg х1 < arctg х2
5. у = 0, якщо х = 0.
6. у > 0, якщо х > 0; у < 0, якщо х < 0.
властивості функції у = arctg х
Слайд 121. D(y)=R.
2. E(y) = (0; π).
3. Графік не симетричний ні відносно
arcctg (-х) = π - arcctg х.
4. Функція спадна. Якщо х1< х2 то
arcctg х1 > arcctg х2.
5. х = 0, якщо у = .
6. у > О для всіх х є R.
властивості функції у = arcctg х.
Слайд 13Домашнє завдання.
М.І. Шкіль.
Розділ 2. §11, ст. 106 запитання 1-4
Ст. № 52 (1-6)
Розв'язати рівняння
a) arcsin(7х – 1) = ; б) arccos(2 – 3х) =




![1. D(y) = [-1; 1].2. Е(у) = .3. Графік симетричний відносно початку координат (функція непарна)](/img/tmb/2/162287/b9fce5d5891fd9fd13bd9359beb6c066-800x.jpg)
![1. D(y) = [-1; 1].2. Е(y)=[0;π].3. Графік не симетричний ні відносно початку координат, ні відносно](/img/tmb/2/162287/70e3f83deb294ebb951ab2009f573554-800x.jpg)