- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Нормальный закон распределения презентация
Содержание
Нормальный закон распределения Рис. 2.2. Смещение кривой нормального распределения при изменении центра рассеивания. Рис. 2.3. Смещение формы кривой нормального
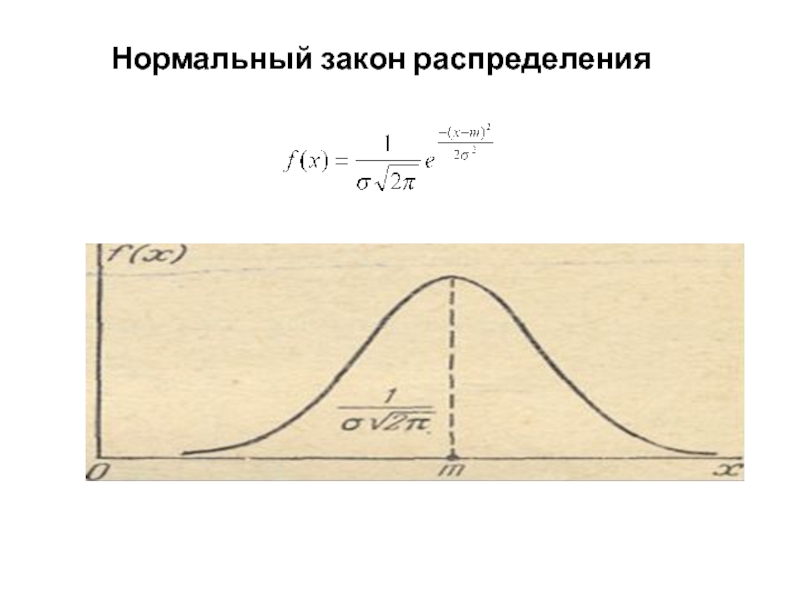
Слайд 2Нормальный закон распределения
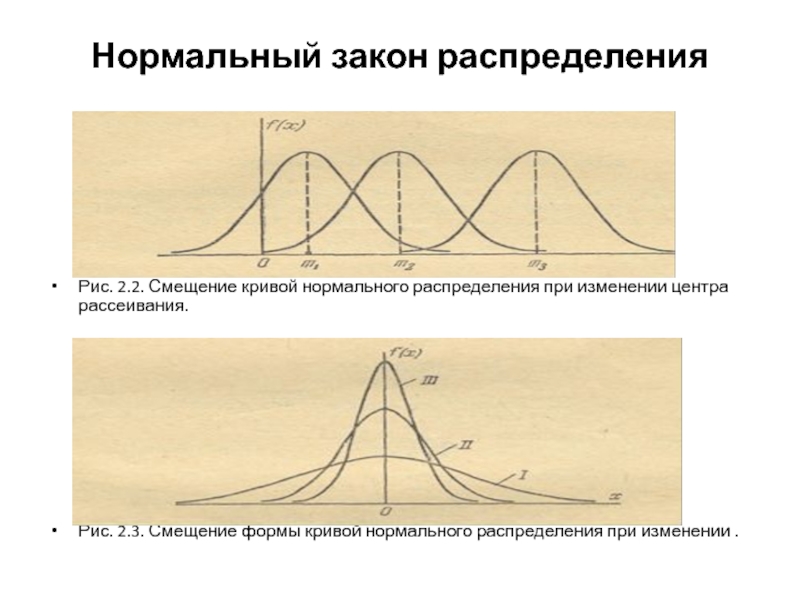
Рис. 2.2. Смещение кривой нормального распределения при изменении центра
рассеивания.
Рис. 2.3. Смещение формы кривой нормального распределения при изменении .
Рис. 2.3. Смещение формы кривой нормального распределения при изменении .
Слайд 3
Вероятность попадания случайной величины,
подчиненной нормальному закону, на заданный участок.
Слайд 4 Вероятность попадания случайной величины, подчиненной нормальному закону, на заданный участок. Как и всякая
функция распределения, функция Ф(х) обладает свойствами:
1. Ф( ) = 0.
2. Ф( ) = 1.
3. Ф(х) - неубывающая функция.
Кроме того, из симметричности нормального распределения с параметрами m = 0, = 1 относительно начала координат следует, что
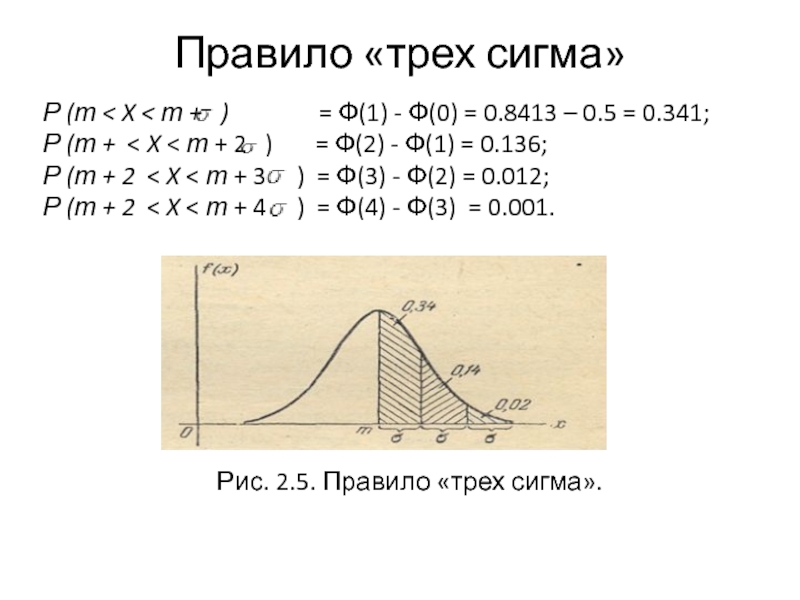
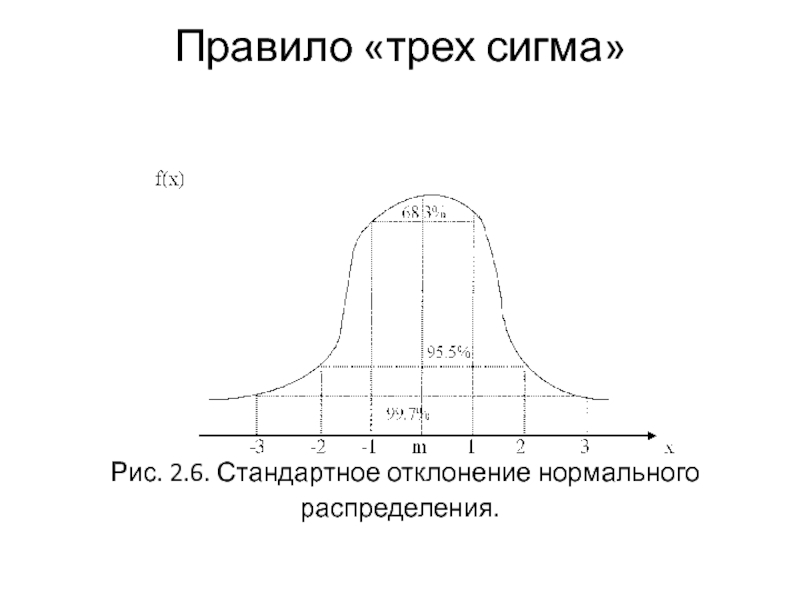
Слайд 5Правило «трех сигма»
Р (т < X < т +
) = Ф(1) - Ф(0) = 0.8413 – 0.5 = 0.341;
Р (т + < X < т + 2 ) = Ф(2) - Ф(1) = 0.136;
Р (т + 2 < X < т + 3 ) = Ф(3) - Ф(2) = 0.012;
Р (т + 2 < X < т + 4 ) = Ф(4) - Ф(3) = 0.001.
Рис. 2.5. Правило «трех сигма».
Рис. 2.5. Правило «трех сигма».
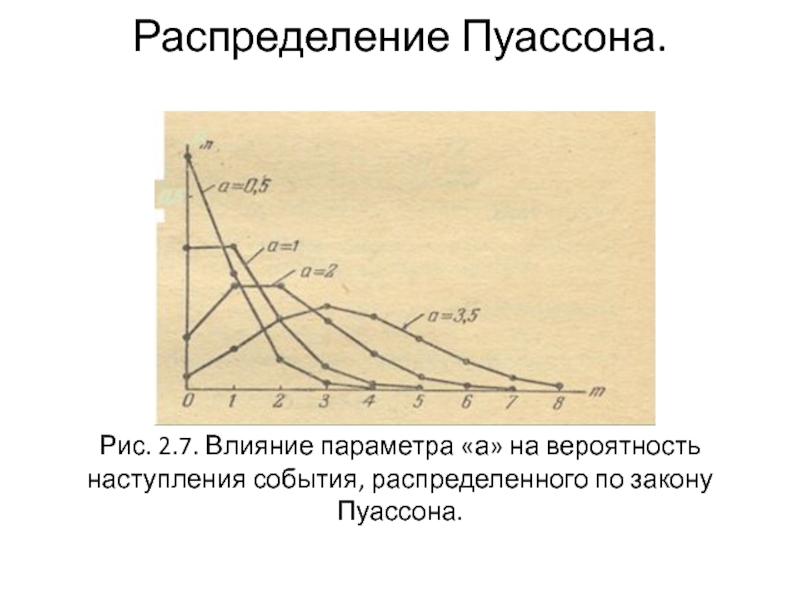
Слайд 8 Распределение Пуассона. Рис. 2.7. Влияние параметра «а» на вероятность наступления события, распределенного
по закону Пуассона.
Слайд 11
Логнормальное распределение.
Рис. 2.8. Плотность вероятностей логнормального распределения.
