- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Непрерывные случайные числа. (Лекция 3) презентация
Содержание
- 1. Непрерывные случайные числа. (Лекция 3)
- 2. Понятие непрерывной случайной величины Непрерывной случайной величиной
- 3. Формы задания закона распределения непрерывной случайной величины
- 4. Свойства функции распределения для непрерывной случайной величины. FX(x)=P(X
- 5. Свойства функции распределения. FX(x)=P(X
- 6. Свойства функции распределения. FX(x)=P(X x1
- 7. Вероятность попадания в интервал X x1
- 8. Плотность распределения Плотность распределения – это
- 9. Свойства плотности распределения 1. φ(х) ≥ 0,
- 10. Вероятность попадания в интервал X1 X2
- 11. Элемент вероятности Пусть Х є [A,B]
- 12. Элемент вероятности φ(x )dx - называют
- 13. Примеры Пример1. Пусть функция распределения случайной величины
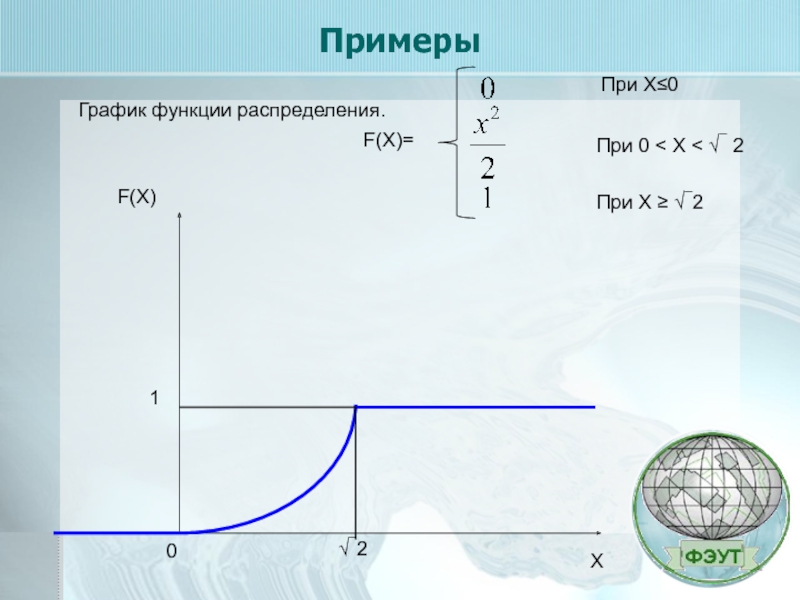
- 14. Примеры График функции распределения. F(X)=
- 15. Примеры F(X)= При Х≤0 При 0
- 16. Графическое представление вероятности попадания в интервал на
- 17. Примеры F(X)= При Х≤0 При 0
- 18. Примеры 5. Построить график плотности распределения. φ(х)
- 19. Графическое представление вероятности попадания в интервал на
- 20. Количественные характеристики законов распределения Функция распределения F(х),
- 21. Характеристики центра распределения Существует три характеристики центра
- 22. Математическое ожидание дискретной случайной величины Рассмотрим следующий
- 23. Математическое ожидание случайной величины Для дискретной случайной
- 24. Математическое ожидание дискретной случайной величины МХ=
- 25. Математическое ожидание непрерывной случайной величины МХ=
- 26. Пример F(X)= При Х≤0 При 0
- 27. Количественные характеристики законов распределения Так как математическое
- 28. Понятие центрального момента Центральным моментом порядка k
- 29. Дисперсия случайной величины μ2= μ2= Наиболее важной
- 30. X φ(X) МX 0 Скошенность
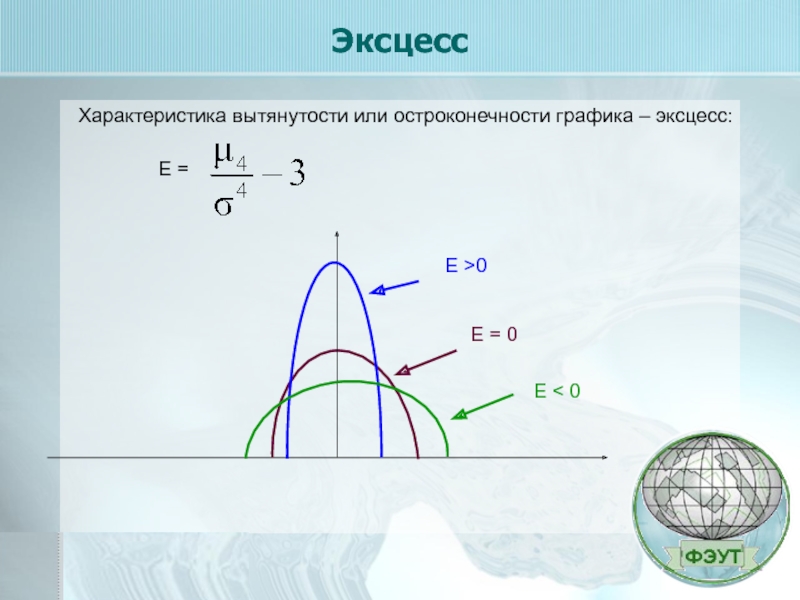
- 31. Эксцесс Характеристика вытянутости или остроконечности графика
- 32. Центральные абсолютные моменты Центральным, абсолютным моментом k
- 33. Свойства математического ожидания 1. Математическое ожидание имеет
- 34. Свойства математического ожидания Докажем третье свойство для
- 35. Спасибо за внимание!
Слайд 2Понятие непрерывной случайной величины
Непрерывной случайной величиной называется такая случайная величина, множество
Например, множество всех значений на отрезке [0,1].
0
1
Каждой точке на отрезке [0,1] соответствует точка на оси абсцисс, и наоборот любой точке оси абсцисс соответствует конкретная точка на отрезке [0,1] . Таким образом устанавливается взаимнооднозначное соответствие. Т.е. мощности множеств отрезка [0,1] и оси абсцисс эквивалентны.
Слайд 3Формы задания закона распределения непрерывной случайной величины
Для непрерывной величины нельзя записать
Но можно задать функцию распределения. F(x) = P(X x X Рассмотрим предел lim Р(x1 ≤Х< x2) x2 1 x2 →x1 x2 →x1 x2 →x1
Если случайная величина непрерывна, то
lim Р(x1 ≤Х< x2)= lim ( F(x2) – F(x1)) = F(x1) – F(x1)=0
Вывод: для непрерывной случайной величины вероятность попадания в точку будет стремиться к нулю.
Слайд 4
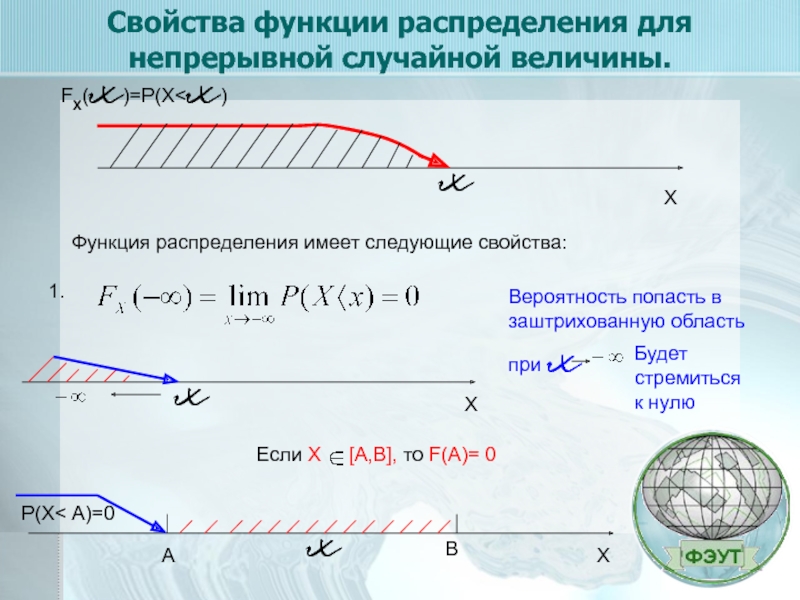
Свойства функции распределения для непрерывной случайной величины.
FX(x)=P(X
1.
X
x
X
x
А
В
Если Х [A,B], то F(А)= 0
Вероятность попасть в заштрихованную область при x
Будет стремиться к нулю
P(X< А)=0
Слайд 5
Свойства функции распределения.
FX(x)=P(X
Будет стремиться к единице
P(X< В)=1, т.к. вероятность попасть в точку, для непрерывной случайной величины равна нулю.
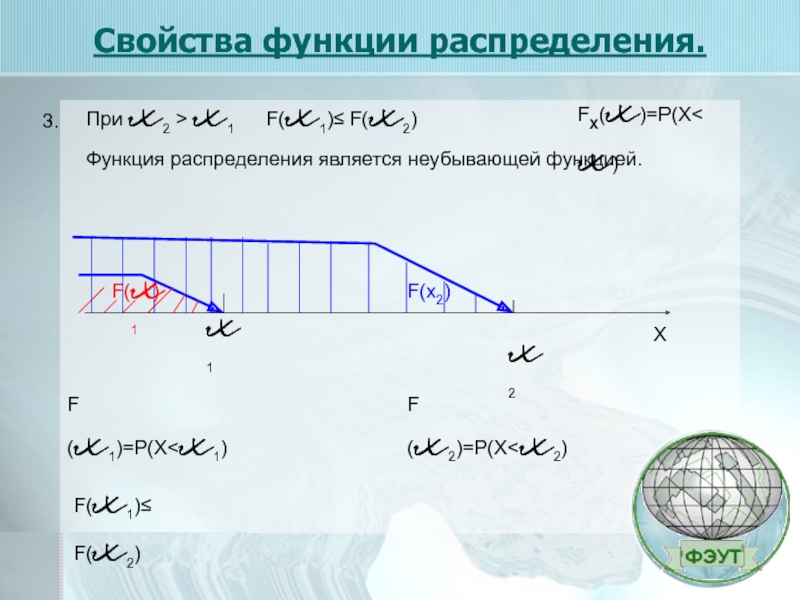
Слайд 6Свойства функции распределения.
FX(x)=P(X x1
x1
x2
Функция распределения является неубывающей функцией.
F (x1)=P(X F (x2)=P(X F(x1)≤ F(x2)
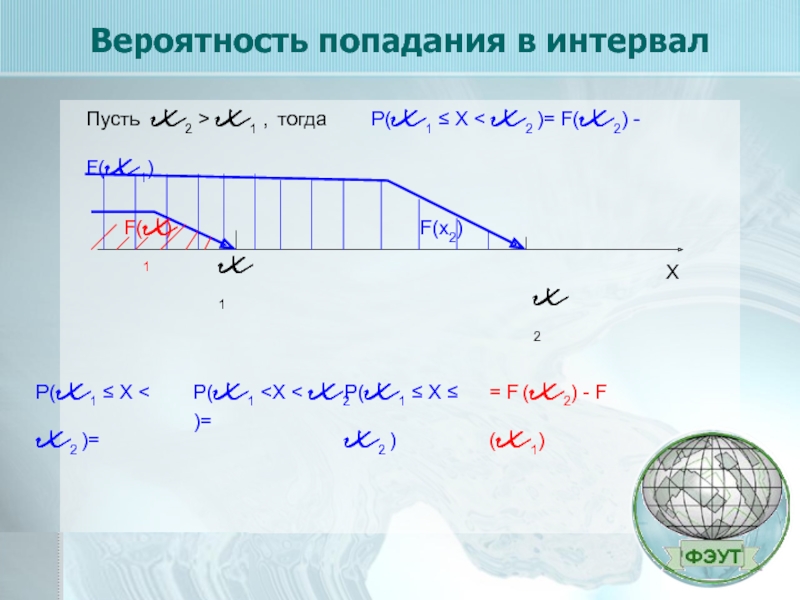
Слайд 7Вероятность попадания в интервал
X
x1
F( )
F(x2)
Пусть x2 > x1 ,
x1
x2
P(x1 ≤ X < x2 )=
= F (x2) - F (x1)
P(x1 ≤ X ≤ x2 )
P(x1
Слайд 8Плотность распределения
Плотность распределения – это производная от функции распределения.
φ(х) =
∆х→0 ∆х
х
Обратная связь: F( х) = ∫ φ(z)dz,
- ∞
F( х) – представляет собой вероятность попадания на отрезок (-∞, х)
Действительно, х
F( х) = ∫ φ(z)dz= F( х) - F(- ∞)= Р (- ∞< х < х) - ∞
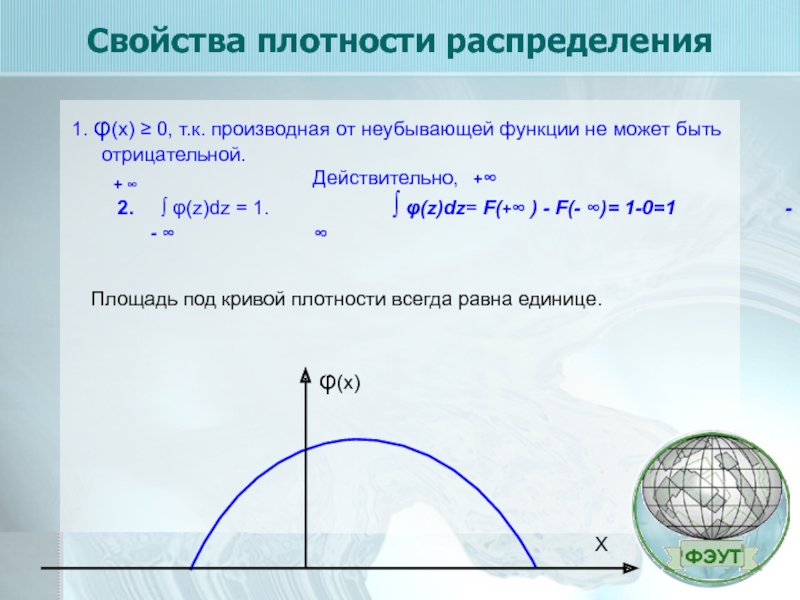
Слайд 9Свойства плотности распределения
1. φ(х) ≥ 0, т.к. производная от неубывающей функции
+ ∞
2. ∫ φ(z)dz = 1.
- ∞
Действительно, +∞
∫ φ(z)dz= F(+∞ ) - F(- ∞)= 1-0=1 - ∞
φ(х)
Х
Площадь под кривой плотности всегда равна единице.
Слайд 10Вероятность попадания в интервал
X1
X2
A
B
X
φ(х)
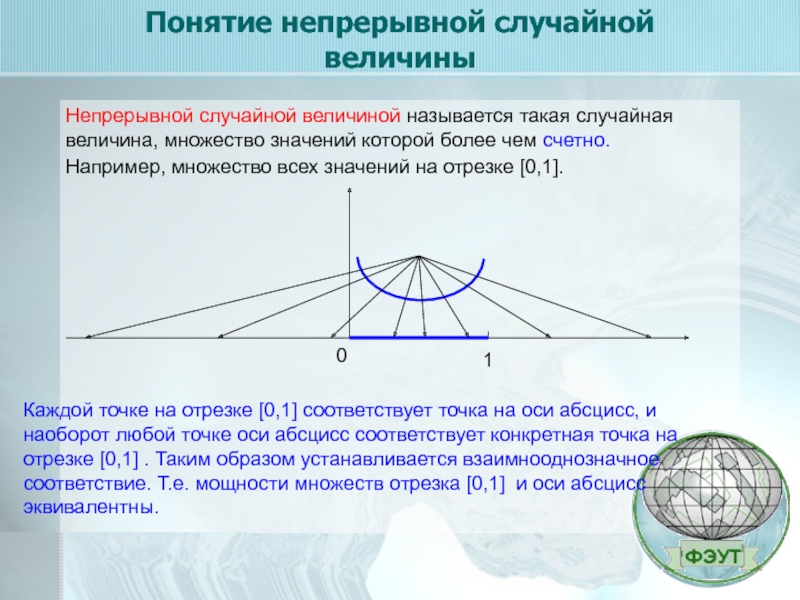
Пусть Х є [A,B] и задана плотность распределения,
Заштрихованная площадь равна
Слайд 11Элемент вероятности
Пусть Х є [A,B]
x
dx
A
B
φ(х)
Х
х+dх
∫ φ(z)dz = F( х+dх) -
Поскольку dx – бесконечно малый отрезок, то φ(x )dx –
F( х+dх) - F(х)= Р (х < X< х + dх ) есть вероятность попадания на бесконечно малый отрезок.
φ(x )dx - называют элементом вероятности.
Слайд 12Элемент вероятности
φ(x )dx - называют элементом вероятности. Это вероятность попадания
В связи с этим данное понятие имеет важное значение.
Понятие вероятности попасть в точку (для дискретных случайных величин) заменяется на элемент вероятности (для непрерывных случайных величин).
φ(x)dx ~ Рi
Вероятность попадания на бесконечно малый отрезок
Вероятность попадания в точку.
Для непрерывных случайных величин
Для дискретных случайных величин
Слайд 13Примеры
Пример1. Пусть функция распределения случайной величины задана кусочно:
х²
F(х) = 2 при А<х<В
1 при х≥В
Требуется:
1. Определить значения А и В.
2. Построить график F(х).
3. Определить вероятность попадания в некоторый интервал
4. Определить φ(х)
5. Построить график φ(х)
Решение: 1. X
[A,B]
F(A)=0
2. X
[A,B]
F(B)=1
Слайд 15Примеры
F(X)=
При Х≤0
При 0 < Х < √¯2
При Х ≥ √¯2
Определим
Р(0.1 < Х < 1) = F(1) - F(0.1) = 1/2-0.12/2=0.5-0.005 = 0.495
Определим вероятность попадания на отрезок Р( -5 < Х < 0.5)
Р(-5 < Х < 0.5) = F(0.5) - F(-5) = 0.52/2 – 0 =0.125 – 0 = 0.125
Определим вероятность попадания на отрезок Р( 8 < Х < 10)
Р(8 < Х < 10) = F(10) – F8) = 1 – 1 = 0
3. Вероятность попадания на отрезок.
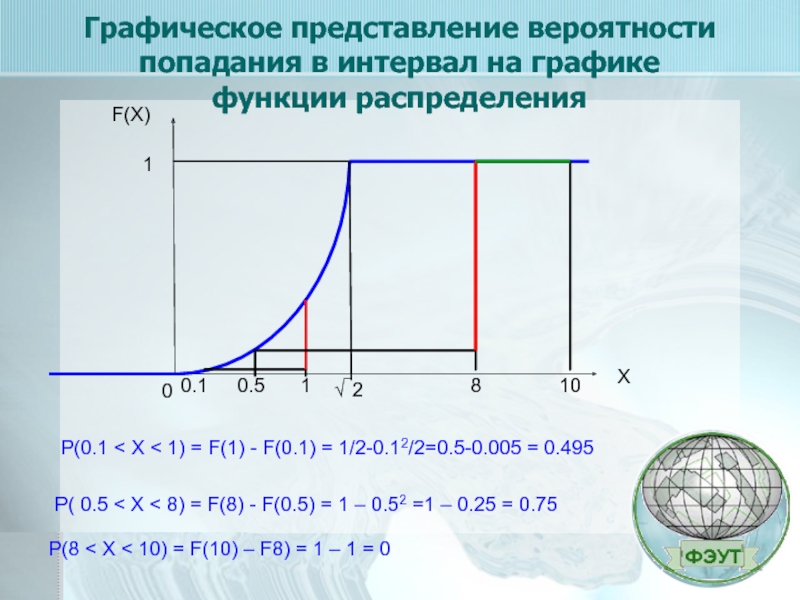
Слайд 16Графическое представление вероятности попадания в интервал на графике функции распределения
F(X)
X
0
√¯2
1
Р(0.1
1
Р( 0.5 < Х < 8) = F(8) - F(0.5) = 1 – 0.52 =1 – 0.25 = 0.75
0.5
Р(8 < Х < 10) = F(10) – F8) = 1 – 1 = 0
8
10
0.1
Слайд 17Примеры
F(X)=
При Х≤0
При 0 < Х < √¯2
При Х ≥ √¯2
4. Определить плотность распределения.
φ(х) = F´(X) =
При Х≤0
При 0 < Х < √¯2
При Х ≥ √¯2
Слайд 18Примеры
5. Построить график плотности распределения.
φ(х) = F´(X) =
При Х≤0
При 0
При Х ≥ √¯2
φ (X)
X
0
√¯2
√¯2
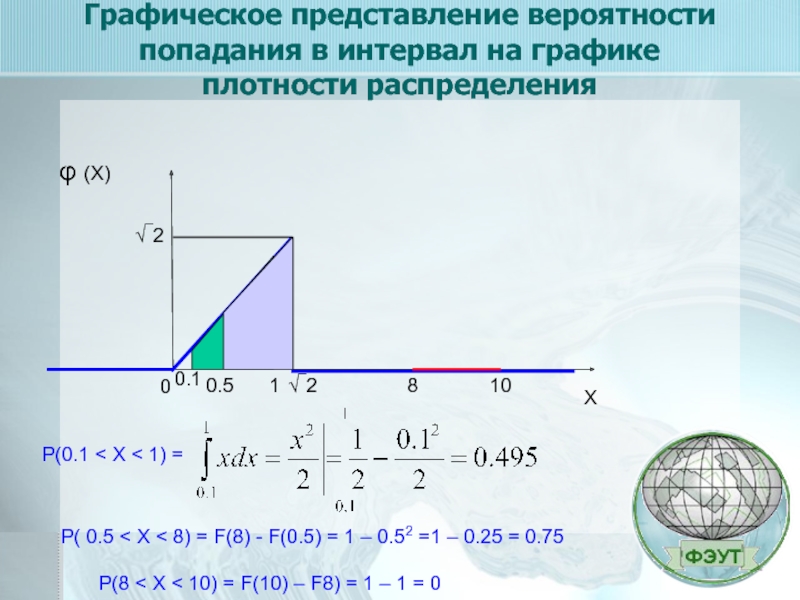
Слайд 19Графическое представление вероятности попадания в интервал на графике плотности распределения
φ (X)
X
0
√¯2
√¯2
Р(0.1 < Х < 1) =
Р( 0.5 < Х < 8) = F(8) - F(0.5) = 1 – 0.52 =1 – 0.25 = 0.75
Р(8 < Х < 10) = F(10) – F8) = 1 – 1 = 0
0.1
1
0.5
8
10
Слайд 20Количественные характеристики законов распределения
Функция распределения F(х), плотность распределения φ(х) и другие
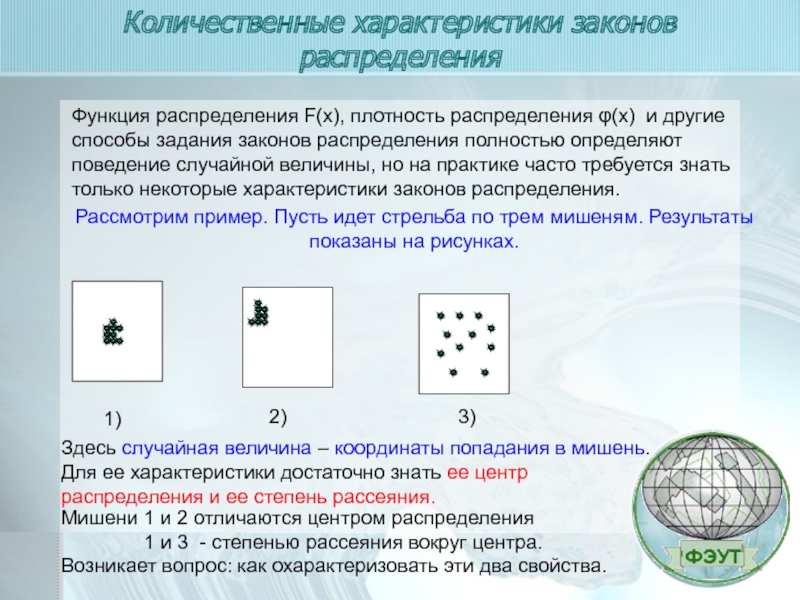
Рассмотрим пример. Пусть идет стрельба по трем мишеням. Результаты показаны на рисунках.
1)
2)
3)
Здесь случайная величина – координаты попадания в мишень. Для ее характеристики достаточно знать ее центр распределения и ее степень рассеяния.
Мишени 1 и 2 отличаются центром распределения
1 и 3 - степенью рассеяния вокруг центра.
Возникает вопрос: как охарактеризовать эти два свойства.
Слайд 21Характеристики центра распределения
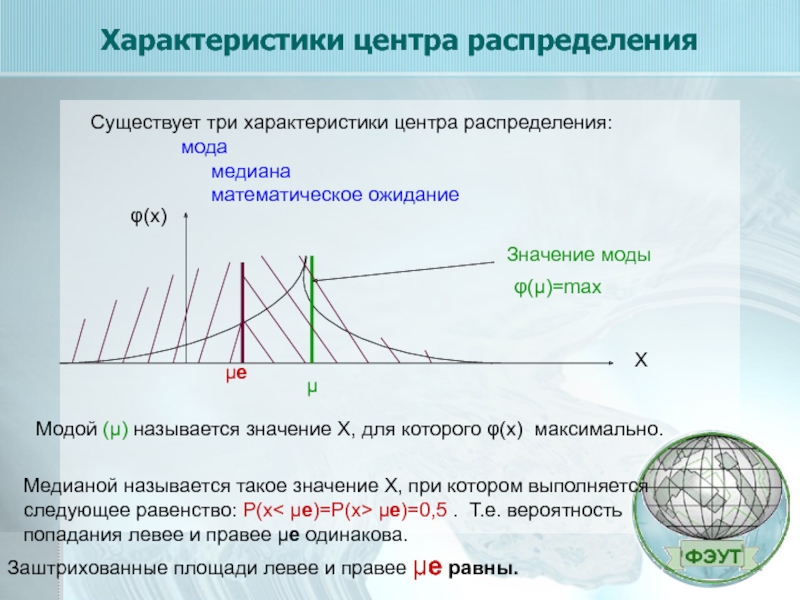
Существует три характеристики центра распределения:
медиана
математическое ожидание
Модой (μ) называется значение X, для которого φ(х) максимально.
Медианой называется такое значение X, при котором выполняется следующее равенство: Р(х< μе)=Р(х> μе)=0,5 . Т.е. вероятность попадания левее и правее μе одинакова.
Х
μ
φ(х)
Значение моды
φ(μ)=max
μе
Заштрихованные площади левее и правее μе равны.
Слайд 22Математическое ожидание дискретной случайной величины
Рассмотрим следующий пример.
Пусть монета подбрасывается 1 раз.
Т.е. необходимо находить некое среднее из возможных значений случайной величины, с учетом вероятностей их появления
(0+1)/2=0.5 - это и есть центр распределения.
Теперь проведем испытания. Подбросим монету 5000 раз. (Опыт Бюффона). Каждый раз будем записывать 1, если появился орел и 0 , если появилась решка. А затем возьмем среднее из всех записанных значений.
Среднее окажется очень близко к 0.5.
Повторим данный эксперимент, с другой монетой, у которой смещен центр тяжести. В силу этого вероятность появления орла при одном бросании будет равна 0.7. В этом случае среднее из нулей и единиц будет близко к 0.7.
Слайд 23Математическое ожидание случайной величины
Для дискретной случайной величины, математическое ожидание, характеризующее центр
МХ=
Здесь
- Возможные значения случайной величины
- Вероятности появления i – го значения случайной величины
Из всех рассмотренных характеристик центра распределения, математическое ожидание проще всего определяется аналитически. Математическое ожидание принято обозначать МХ или М[X].
Слайд 24Математическое ожидание дискретной случайной величины
МХ=
Рассмотрим пример.
Распределение случайной величины Х
= -2*0.2 - 1*0.1+ 0*0.2 + 4*0.3 + 5*0.1 + 8*0.1 = 2.0
Слайд 25Математическое ожидание непрерывной случайной величины
МХ=
- Для дискретной случайной величины.
Аналогично, можно
Вместо
, необходимо взять элемент вероятности φ(х)dх
А ∑ заменить на ∫. Тогда получим формулу.
МХ=
- Для непрерывной случайной величины.
Слайд 26Пример
F(X)=
При Х≤0
При 0 < Х < √¯2
При Х ≥ √¯2
Плотность распределения.
φ(х) = F´(X) =
При Х≤0
При 0 < Х < √¯2
При Х ≥ √¯2
Здесь математическое ожидание будет
Слайд 27Количественные характеристики законов распределения
Так как математическое ожидание легко определяется аналитически, то
На основе математического ожидания введены понятия начальных, центральных, абсолютных центральных моментов.
Начальным моментом порядка k называется математическое ожидание случайной величины Х в степени k.
Так, первый начальный момент есть математическое ожидание.
Формулы вычисления начального момента:
Для дискретной случайной величины
Для непрерывной случайной величины
αk=
αk=
α1=
Слайд 28Понятие центрального момента
Центральным моментом порядка k называется математическое ожидание центрированной случайной
Формулы вычисления начального момента:
Для дискретной случайной величины
Для непрерывной случайной величины
μk=
μk=
Слайд 29Дисперсия случайной величины
μ2=
μ2=
Наиболее важной характеристикой среди центральных моментов является второй центральный
Дисперсия имеет размерность квадрата размерности случайной величины, что неудобно. Поэтому, чаще используют квадратный корень из дисперсии, который обозначают σХ и называют – среднее квадратическое отклонение.
σХ= +√¯DX
Слайд 30
X
φ(X)
МX
0
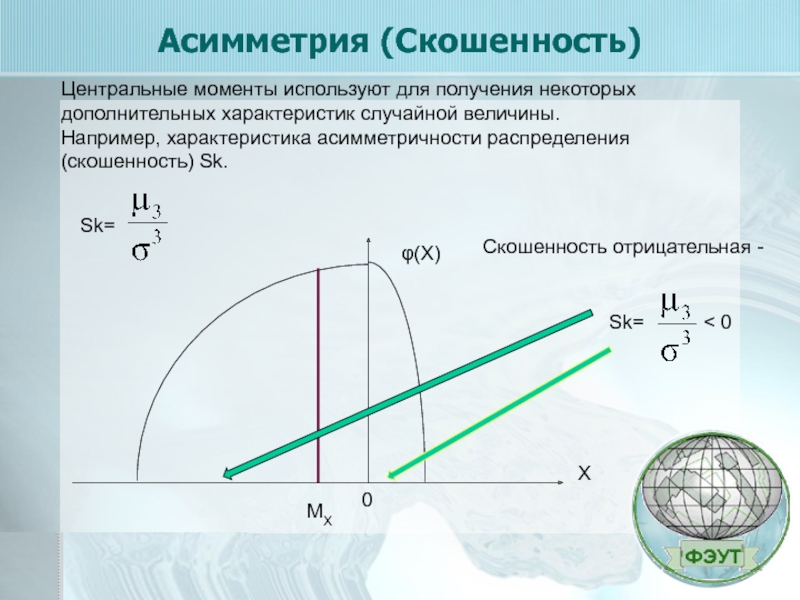
Скошенность отрицательная -
Sk=
< 0
Центральные моменты используют для получения некоторых дополнительных
Например, характеристика асимметричности распределения (скошенность) Sk.
Асимметрия (Скошенность)
Sk=
Слайд 32Центральные абсолютные моменты
Центральным, абсолютным моментом k –го порядка называется математическое ожидание
Обычно при расчетах используют только первый центральный момент:
С точки зрения теории ошибок, величина X-MX представляет собой истинную ошибку измерений Δ.
Величину
называют средним отклонением.
Слайд 33Свойства математического ожидания
1. Математическое ожидание имеет размерность случайной величины.
2. Мс =
3. Мсх = сМх
4. Мх+у = Мх + Му
5.
7. М ≈ ƒ (Мх1, Мх2,…,Мхn)
6. МX•Y = МX • МY
ƒ(х1, х2,… хn)
Доказательство.
2. MC =
3. Мсх = сМх
Слайд 34Свойства математического ожидания
Докажем третье свойство для непрерывной случайной величины.
Рассмотрим функцию распределения
FсХ(x) = Р(сХ< x) = Р(Х< x/с) = FХ(x/с)
Возьмем производные от левой и правой частей полученного равенства:
φсХ(x) = φХ(x/с)/с
+∞ МсХ =∫ x φсХ(x)dx
-∞
=∫x/c φХ(x/c)dx
+∞
-∞
= с∫x/cφХ(x/c)d(x/c) = cМх
+∞
-∞




![Вероятность попадания в интервалX1X2ABXφ(х)Пусть Х є [A,B] и задана плотность распределения, график которой приведен ниже.Заштрихованная](/img/tmb/3/252251/de272e9e6e5e80877a5259e7604122c5-800x.jpg)
![Элемент вероятностиПусть Х є [A,B]xdxABφ(х)Х х+dх∫ φ(z)dz = F( х+dх) - F(х)= Р (х <](/img/tmb/3/252251/31cf93497cbbdb9cfa7b73acbae7773b-800x.jpg)