- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Неопределённый интеграл презентация
Содержание
- 1. Неопределённый интеграл
- 6.
- 7. Способ подстановки ( метод замены переменных).
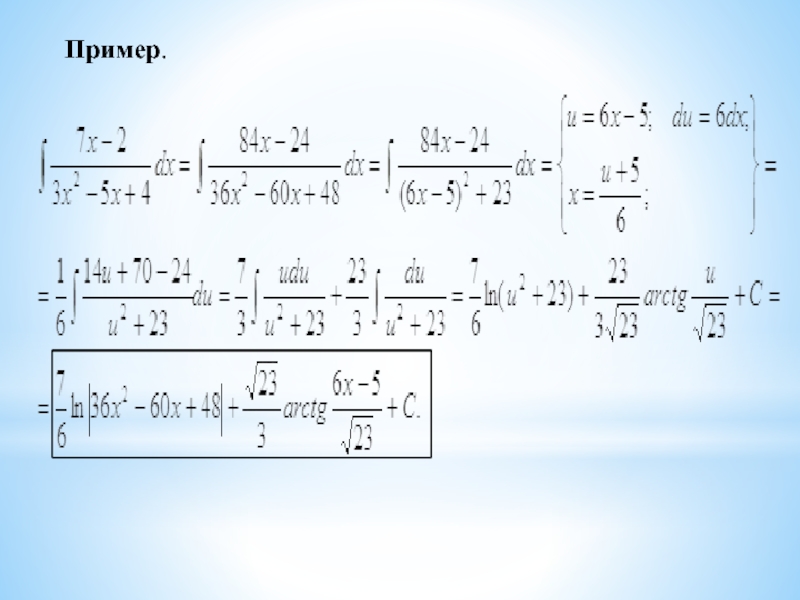
- 8. Пример.
- 9. Разложение дробно - рациональной функции на элементарные
- 10. Пример. Разложить функцию
- 11. Интегрирование простейших элементарных дробей
- 12. Пример.
- 13. Пример. Пример.
- 14. Общая схема интегрирование рациональных дробей вида
- 15. Пример:
- 16. Пример Найти I =
- 17. R - рациональная функции от переменных
- 18. Пример.
Слайд 5 7.1.
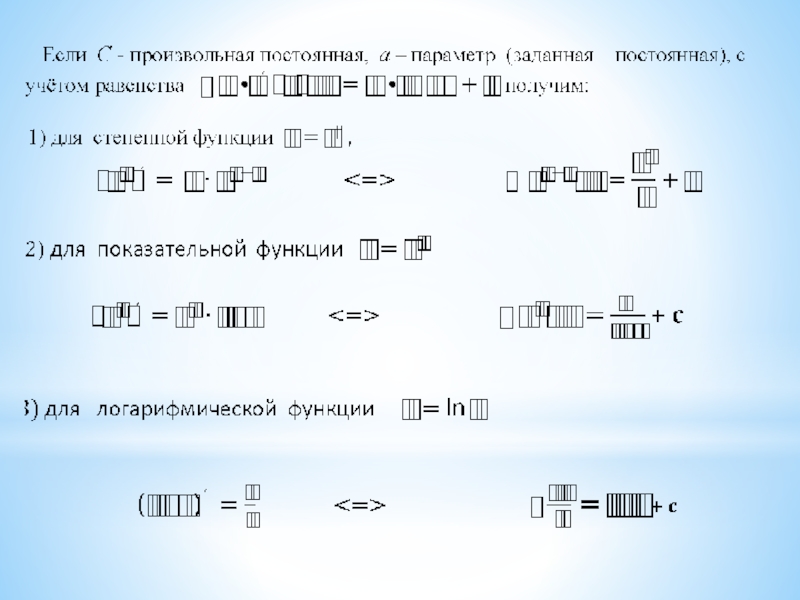
Функция F(x) называется первообразной функцией функции f(x) на отрезке [a, b], если в любой точке этого отрезка верно равенство: F′(x) = f(x).
Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением F(x) + C.
Слайд 9Разложение дробно - рациональной функции на элементарные дроби по методу неопределённых
P(x) = (x - a)α…(x - b)β(x2 + px + q)λ…(x2 + rx + s)μ
знаменатель которой
Для нахождения величин Ai, Bi, Mi, Ni, Ri, Si применяют так называемый метод неопределенных коэффициентов, суть которого состоит в том, что для того, чтобы два многочлена были тождественно равны, необходимо и достаточно, чтобы были равны коэффициенты при одинаковых степенях х.
то эта дробь может быть разложена на элементарные по следующей схеме:
Слайд 14Общая схема интегрирование рациональных дробей вида
M, N, a, b, c, n
Слайд 16Пример Найти I =
Т.к. дробь неправильная, то
предварительно
I