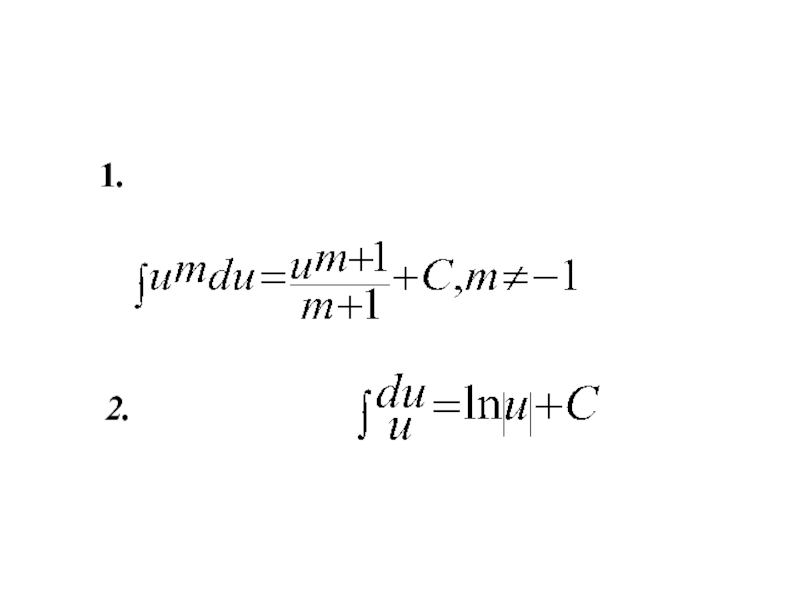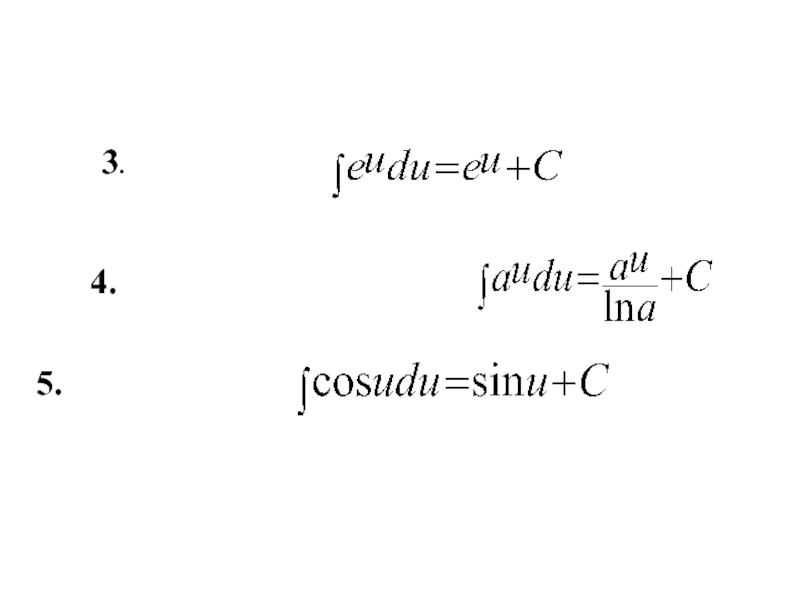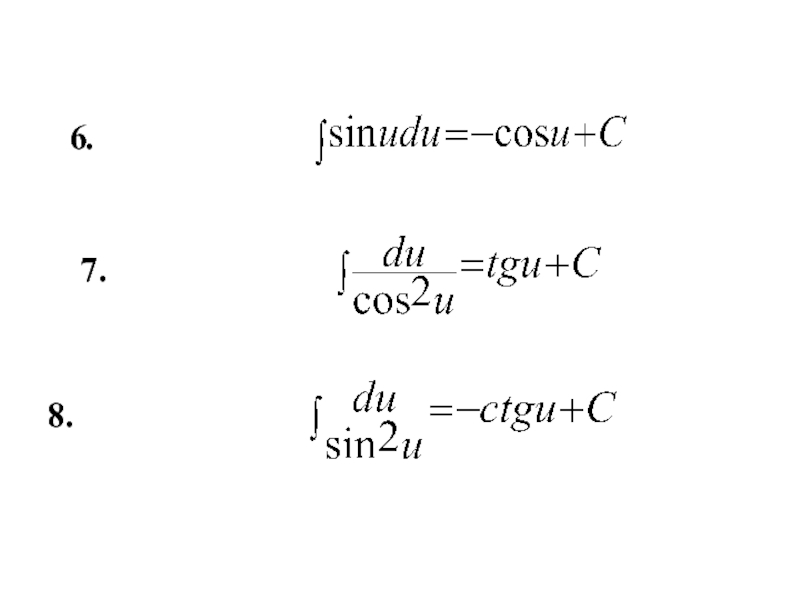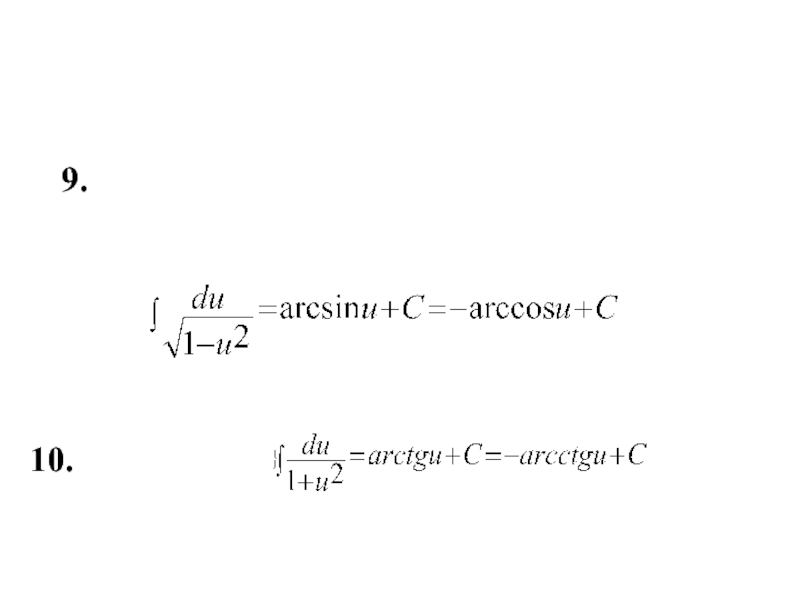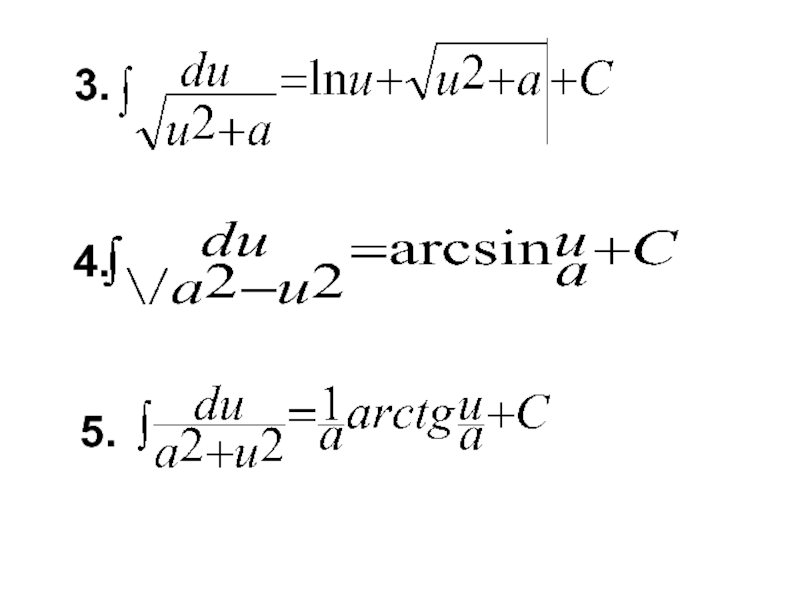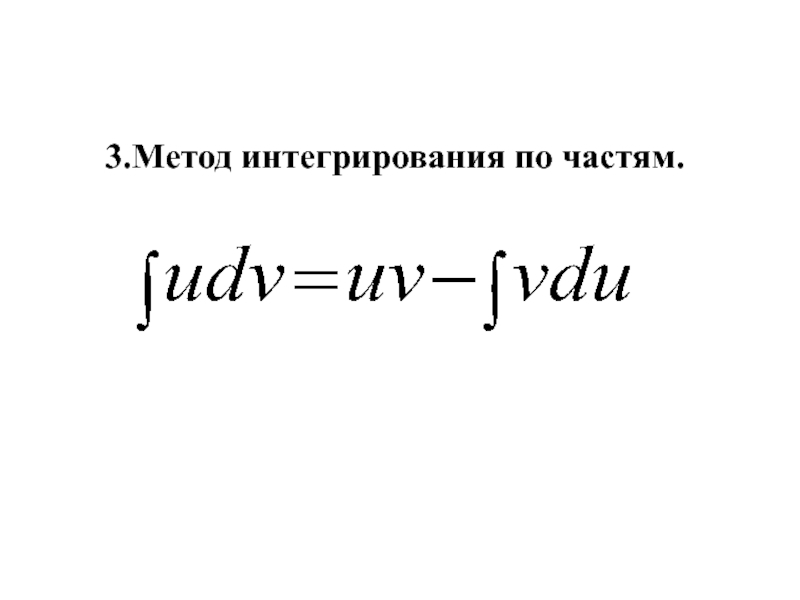- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Неопределенный интеграл. Определения и теоремы презентация
Содержание
- 1. Неопределенный интеграл. Определения и теоремы
- 2. Определения и теоремы: Определение. Первообразной функцией для
- 3. Теорема. Две различные первообразные одной и той
- 4. Определение. Общее выражение для всех первообразных данной
- 5. Свойства неопределенного интеграла 1.Если непрерывно дифференцируемая
- 6. 3. Неопределенный интеграл от алгебраической суммы конечного
- 7. 2.Таблица простейших неопределенных интегралов Таблица интегралов
- 8. 1. 2.
- 9. 5. 4. 3.
- 10. 7. 8. 6.
- 11. 10. 9.
- 12. Дополнительные формулы: 1. 2.
- 13. 3. 4. 5.
- 14. 3.Основные методы интегрирования :
- 15. 2.Метод подстановки (метод введения новой переменной)
- 16. 3.Метод интегрирования по частям.
- 17. Неберущиеся интегралы
- 18. Теорема Коши Теорема: Всякая непрерывная функция имеет первообразную (от всякой непрерывной функции существует неопределенный интеграл).
Определения и теоремы: Определение. Первообразной функцией для данной функции f(x) на данном промежутке называется, такая функция F(x), производная которой равна f(x) или дифференциал которой равен f(x)dx на рассматриваемом промежутке.
Слайд 2Определения и теоремы:
Определение. Первообразной функцией для данной функции f(x) на данном
промежутке называется, такая функция F(x), производная которой равна f(x) или дифференциал которой равен f(x)dx на рассматриваемом промежутке.
Слайд 3Теорема. Две различные первообразные одной и той же функции, определенной в
некотором промежутке, отличаются друг от друга на этом промежутке на const.
Слайд 4Определение. Общее выражение для всех первообразных данной непрерывной функции f(x) называется
неопределенным интегралом от функции f(x) или от дифференциального выражения f(x)dx и обозначается символам .
Слайд 63. Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен
алгебраической сумме неопределенных интегралов от этих функций.
Слайд 18Теорема Коши
Теорема: Всякая непрерывная функция имеет первообразную (от всякой непрерывной функции
существует неопределенный интеграл).
