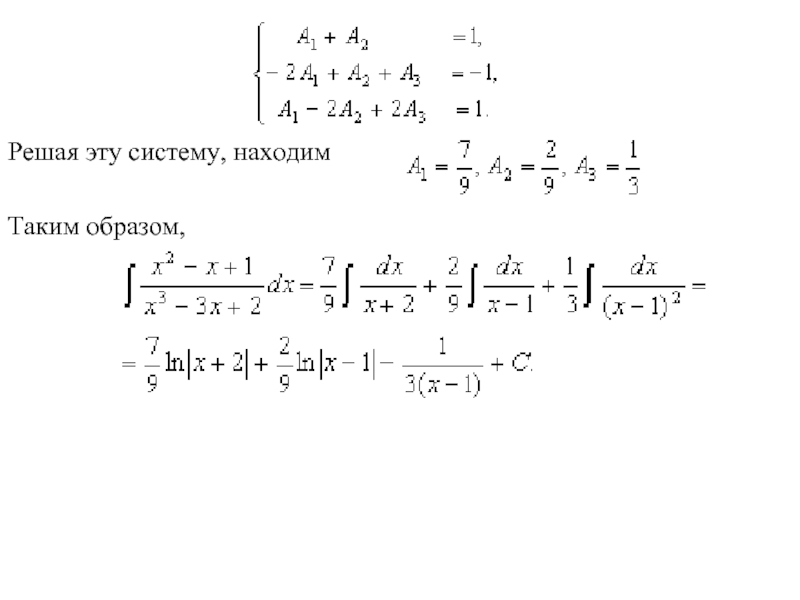- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Неопределенный интеграл. Интегрирование функций, содержащих квадратный трехчлен. Лекция 3 презентация
Содержание
- 1. Неопределенный интеграл. Интегрирование функций, содержащих квадратный трехчлен. Лекция 3
- 2. Интегрировании функций, содержащих квадратный трехчлен в
- 3. Примеры. 1)
- 4. Пример
- 5. Пример Найти
- 6. Интегрирование рациональных дробей Рациональная дробь есть отношение
- 7. Каждая правильная дробь
- 8. Схема разложения на простейшие слагаемые правильных рациональных дробей
- 9. Одним из способов нахождения коэффициентов
- 10. ПРИМЕРЫ 1. Найти
- 11. Решая эту систему, находим Таким образом,
- 13. Получаем Интеграл, соответственно, равен
- 14. Отсюда получаем Подынтегральное
- 15. Отсюда получаем Подынтегральное
- 16. Примеры. 1)
Слайд 2
Интегрировании функций, содержащих квадратный трехчлен в знаменателе дроби. При этом, независимо
от того, стоит ли квадратный трехчлен под знаком квадратного корня или нет, интегрирование проводится по следующей схеме:
1) в квадратном трехчлене выделяется полный квадрат
2)полученный интеграл, при необходимости, разбивается на два интеграла, один из которых – всегда табличный, а другой приводится к табличному подведением под знак дифференциала.
1) в квадратном трехчлене выделяется полный квадрат
2)полученный интеграл, при необходимости, разбивается на два интеграла, один из которых – всегда табличный, а другой приводится к табличному подведением под знак дифференциала.
Слайд 6Интегрирование рациональных дробей
Рациональная дробь есть отношение двух многочленов целой степени
Если
, то дробь называется правильной. Если , то дробь называется неправильной.
Прежде, чем интегрировать неправильную дробь, следует выделить целую часть дроби путем деления многочлена
на многочлен .
Пример
Дробь представляется в виде суммы целой части (многочлена целой степени) и правильной дроби.
Прежде, чем интегрировать неправильную дробь, следует выделить целую часть дроби путем деления многочлена
на многочлен .
Пример
Дробь представляется в виде суммы целой части (многочлена целой степени) и правильной дроби.
Слайд 7
Каждая правильная дробь
может быть представлена в виде суммы конечного числа простых дробей.
При этом разложение правильной дроби на простые дроби связано с разложением знаменателя этой дроби на простые множители.
Простейшей дробью называется дробь одного из следующих четырех типов:
1) 2)
3) 4)
Где - постоянные числа, k - целое.
При этом разложение правильной дроби на простые дроби связано с разложением знаменателя этой дроби на простые множители.
Простейшей дробью называется дробь одного из следующих четырех типов:
1) 2)
3) 4)
Где - постоянные числа, k - целое.
Слайд 9
Одним из способов нахождения коэффициентов А, B, C, D, E
в разложении правильной рациональной дроби является следующий.
1) Правую часть полученного разложения с неопределенными коэффициентами А, B, C, D, E приводят к общему знаменателю. Так как знаменатели правой и левой частей равны, то должны быть равны и числители, которые являются полиномами.
2)Приравнивая коэффициенты при одинаковых степенях х (так как полиномы равны, если равны коэффициенты при одинаковых степенях х).
3) Получаем систему линейных уравнений для определения этих коэффициентов.
1) Правую часть полученного разложения с неопределенными коэффициентами А, B, C, D, E приводят к общему знаменателю. Так как знаменатели правой и левой частей равны, то должны быть равны и числители, которые являются полиномами.
2)Приравнивая коэффициенты при одинаковых степенях х (так как полиномы равны, если равны коэффициенты при одинаковых степенях х).
3) Получаем систему линейных уравнений для определения этих коэффициентов.
Слайд 10ПРИМЕРЫ
1. Найти
Корни знаменателя – x1 = -2 кратности 1 и x2=1 кратности 2. Поэтому x3 – 3x + 2 = (x+2)(x-1)2 и подынтегральная функция может быть представлена в виде
Приводя к общему знаменателю, получаем
Приравнивая коэффициенты при одинаковых степенях x в числителях правой и левой частей, получаем
Слайд 12 ПРИМЕРЫ
2. Найти
Разложим подынтегральное
выражение на сумму простейших дробей, используя метод неопределенных коэффициентов:
Следовательно,
Следовательно,
Слайд 13
Получаем
Интеграл, соответственно, равен
3. Найти
Разложим подынтегральное выражение на сумму двух дробей.
Найдем неизвестные
коэффициенты.