Экономическая интерпретация параметров модели. Коэффициенты корреляции и детерминации в линейной модели парной регрессии.
Оценка значимости уравнения регрессии в целом. Оценка значимости отдельных параметров регрессии.
Расчет доверительных интервалов для параметров регрессии. Интервалы прогноза по линейному уравнению регрессии.
Нелинейная регрессия. Индекс корреляции.
Линеаризация нелинейных регрессий.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Экономическая и статистическая интерпретация линейной модели парной регрессии. Нелинейная регрессия. (Тема 2) презентация
Содержание
- 1. Экономическая и статистическая интерпретация линейной модели парной регрессии. Нелинейная регрессия. (Тема 2)
- 2. Экономическая интерпретация параметров модели. Коэффициенты корреляции и детерминации в линейной модели парной регрессии.
- 3. Задача: начальник отдела маркетинга кинотеатра «Отражение»
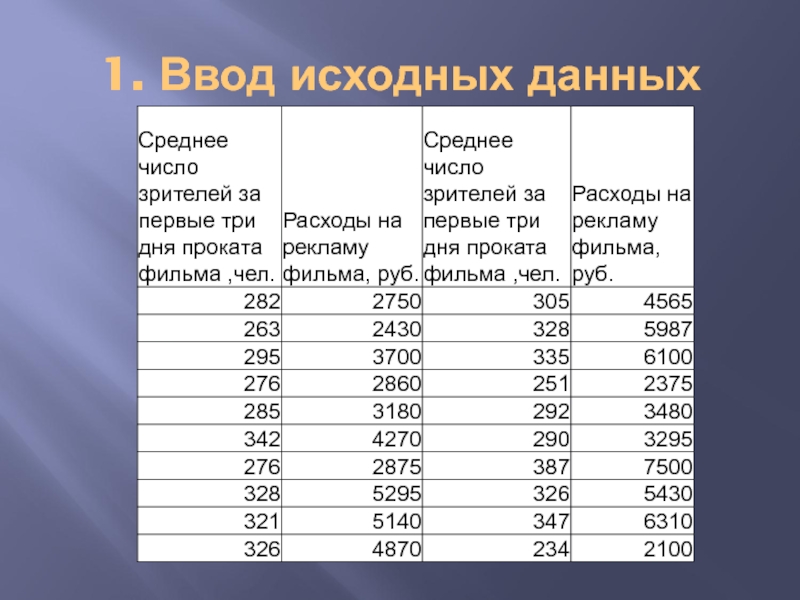
- 4. 1. Ввод исходных данных
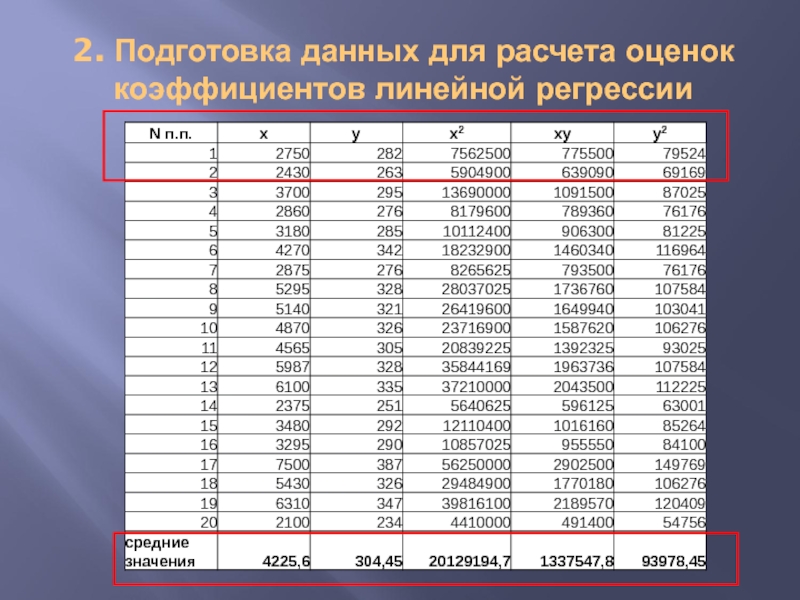
- 5. 2. Подготовка данных для расчета оценок коэффициентов линейной регрессии
- 6. 3. Расчет оценок коэффициентов регрессии
- 7. Коэффициент b этой модели показывает, что
- 8. Диаграмма Венна Если все точки лежат на
- 9. Линейный коэффициент парной корреляции Если b>0, то ryx>0; если b
- 10. По абсолютной величине чем ближе значение rxy
- 12. Суммы квадратов отклонений - Общая с.
- 13. Выборочные оценки дисперсий - Общая дисперсия - Остаточная дисперсия - Регрессионная дисперсия
- 14. Коэффициент детерминации Коэффициент детерминации определяет долю разброса
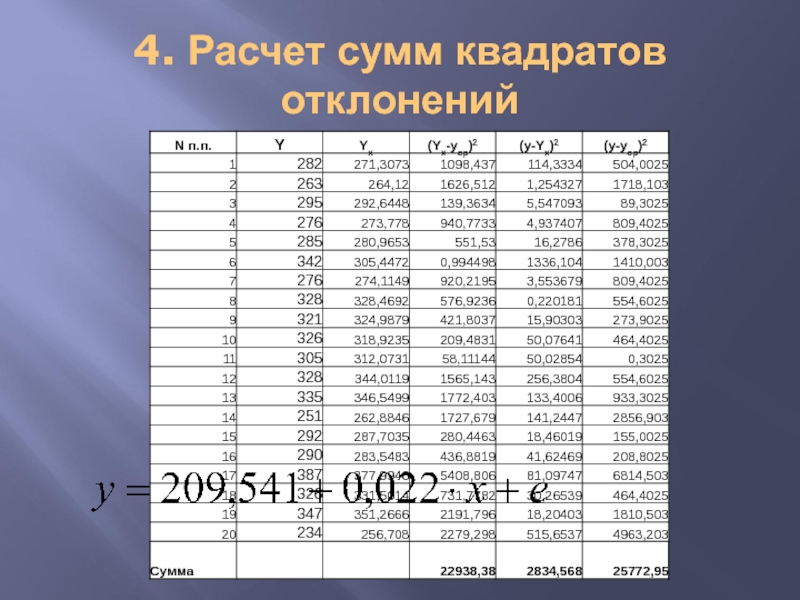
- 15. 4. Расчет сумм квадратов отклонений
- 16. 5. Расчет коэффициентов корреляции и детерминации
- 17. Коэффициент корреляции достаточно высокий (0,94), что
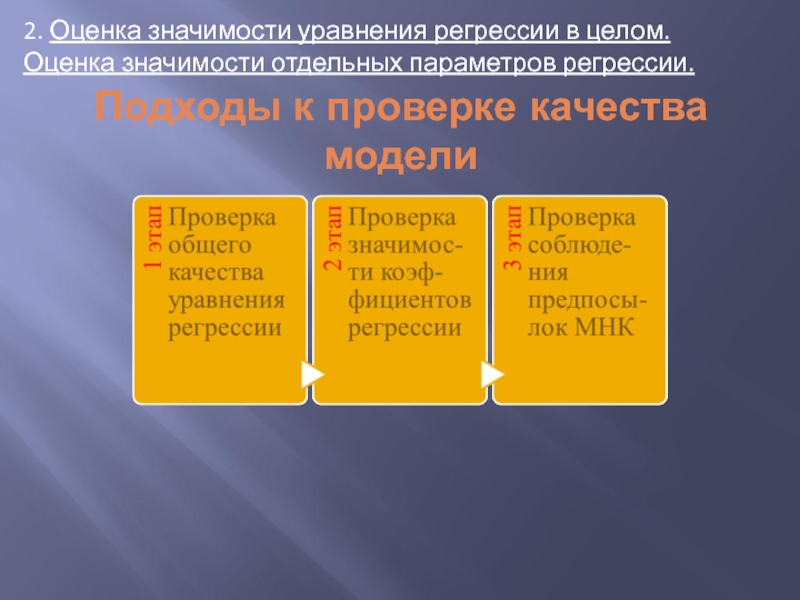
- 18. Подходы к проверке качества модели 2.
- 19. Оценка значимости уравнения регрессии в целом F-тест
- 20. 1. Расчет выборочных оценок дисперсий
- 21. 2. Расчет наблюдаемого значения Фишера и его
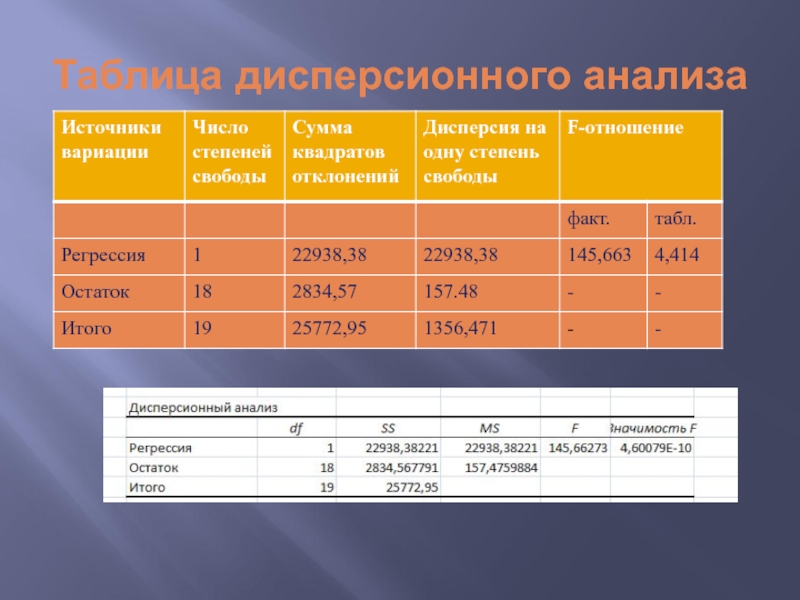
- 22. Таблица дисперсионного анализа
- 23. Оценка значимости отдельных параметров уравнения регрессии T-тест
- 24. Стандартные ошибки параметров регрессии
- 25. 2. Расчет стандартных ошибок параметров регрессии
- 26. 2. Расчет наблюдаемого значения Стьюдента и его
- 27. Доверительные интервалы коэффициентов теоретического уравнения регрессии 3.
- 28. 3. Расчет доверительных границ для параметров регрессии
- 29. Предсказание среднего значения зависимой переменной По уравнению
- 30. Предсказание индивидуальных значений зависимой переменной myxp –
- 31. 6. Получение прогнозной оценки числа зрителей и расчет доверительных границ
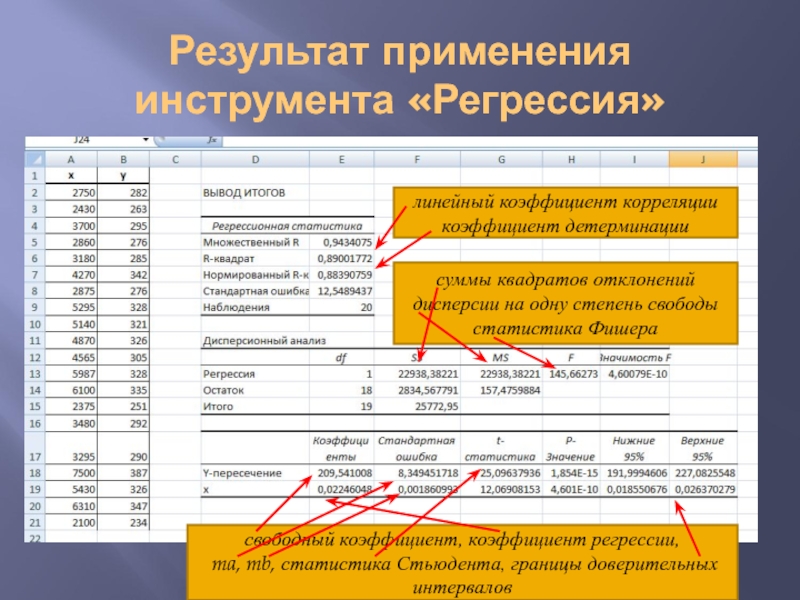
- 32. Результат применения инструмента «Регрессия» линейный коэффициент корреляции
- 33. Классы нелинейных регрессий 4. Нелинейная регрессия. Индекс корреляции.
- 34. Регрессии, нелинейные относительно переменных
- 35. Регрессии, нелинейные по оцениваемым параметрам
- 36. Индекс корреляции Для измерения тесноты
- 37. 5. Линеаризация нелинейных регрессий.
- 38. Замена переменных заключается в замене нелинейных
- 39. Гиперболическая модель
- 40. Кривая Филлипса (равносторонняя гипербола) х- норма безработицы, y – процент прироста заработной платы
- 41. Кривая Энгеля х- доход потребителей,
- 42. Полулогарифмические модели Такие модели обычно используются в
- 43. Используется обычно в тех случаях, когда необходимо
- 44. Логарифмирование обеих частей уравнения применяется обычно,
- 45. К классу степенных функций относятся: кривые спроса
- 46. Показательные (экспоненциальные) модели Широкий класс экономических показателей
- 47. Показательные (экспоненциальные) модели
- 48. Логистическая кривая Применяется для описания поведения показателей,
- 49. Логлинейная модель Используется в банковском и финансовом
- 50. Коэффициент эластичности Величина коэффициента эластичности показывает, на
- 51. Расчет коэффициента эластичности
- 52. Расчет коэффициента эластичности
Экономическая интерпретация параметров модели. Коэффициенты корреляции и детерминации в линейной модели парной регрессии.
Слайд 1Тема 2. Экономическая и статистическая интерпретация линейной модели парной регрессии. Нелинейная
регрессия.
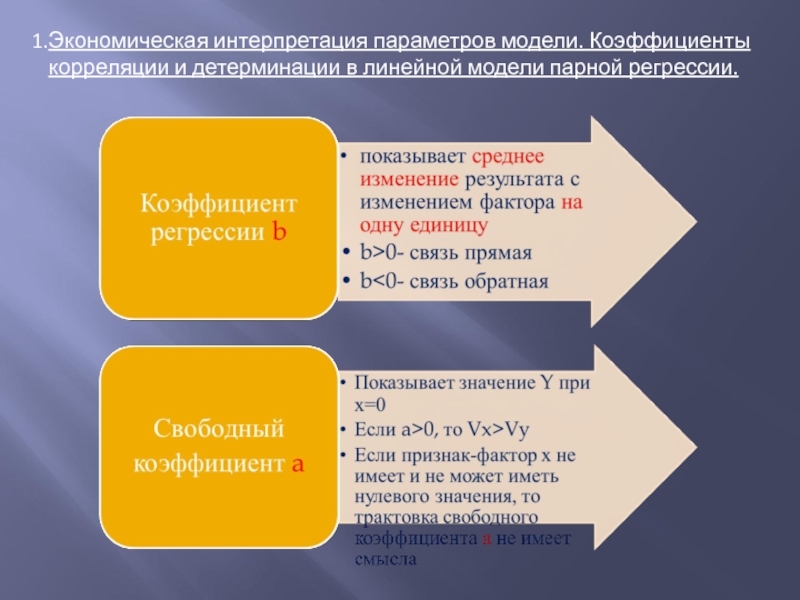
Слайд 2Экономическая интерпретация параметров модели. Коэффициенты корреляции и детерминации в линейной модели
парной регрессии.
Слайд 3Задача: начальник отдела маркетинга кинотеатра «Отражение» поручил своим сотрудникам провести
исследование, в результате которого необходимо:
выявить фактор, в наибольшей степени влияющий на среднее число зрителей за первые три дня проката фильма;
2) построить прогнозную модель в виде линейной функции;
3) с помощью построенной модели получить прогнозные оценки среднего числа зрителей на первые три дня проката следующего фильма, при расходах на рекламу в 5000 руб.
выявить фактор, в наибольшей степени влияющий на среднее число зрителей за первые три дня проката фильма;
2) построить прогнозную модель в виде линейной функции;
3) с помощью построенной модели получить прогнозные оценки среднего числа зрителей на первые три дня проката следующего фильма, при расходах на рекламу в 5000 руб.
Слайд 7Коэффициент b этой модели показывает, что
в среднем увеличение расходов на
рекламу на
1000 рублей приводит к увеличению числа
зрителей за первые три дня проката фильма
на 22 человека.
1000 рублей приводит к увеличению числа
зрителей за первые три дня проката фильма
на 22 человека.
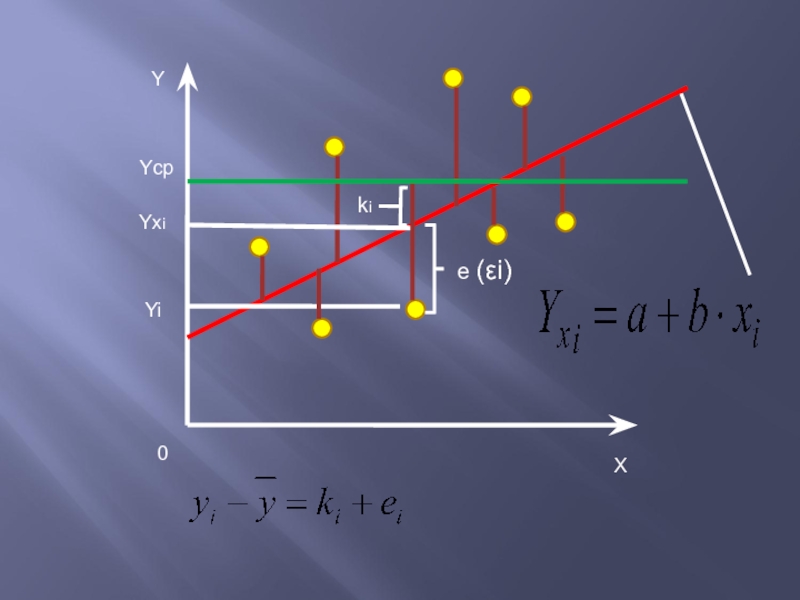
Слайд 8Диаграмма Венна
Если все точки лежат на построенной прямой, то регрессия Y
на Х
«идеально» объясняет поведение зависимой переменной. Обычно
поведение Y лишь частично объясняется влиянием переменной Х.
«идеально» объясняет поведение зависимой переменной. Обычно
поведение Y лишь частично объясняется влиянием переменной Х.
X
Y
X
X
Y
Y
X
Y=X
Y
2 вопрос
Слайд 10По абсолютной величине чем ближе значение rxy к единице, тем
теснее
связь, чем ближе значение rxy к нулю, тем слабее связь
Слайд 12Суммы квадратов отклонений
- Общая с. к.о. (TSS)
- Регрессионная с. к.
о. (ESS)
- Остаточная с.к.о. (RSS)
Слайд 14Коэффициент детерминации
Коэффициент детерминации определяет долю разброса
зависимой переменной Y, объяснимую регрессией
Y на X.
Слайд 17Коэффициент корреляции достаточно
высокий (0,94), что свидетельствует о
существенной зависимости числа
зрителей
за первые три дня проката фильма от
расходов на рекламу.
Коэффициент детерминации также
достаточно высокий, он показывает, что
89% разброса числа зрителей за первые
три дня проката фильма объясняется
зависимостью с расходами на рекламу.
за первые три дня проката фильма от
расходов на рекламу.
Коэффициент детерминации также
достаточно высокий, он показывает, что
89% разброса числа зрителей за первые
три дня проката фильма объясняется
зависимостью с расходами на рекламу.
Слайд 18Подходы к проверке качества модели
2. Оценка значимости уравнения регрессии в
целом. Оценка значимости отдельных параметров регрессии.
Слайд 19Оценка значимости уравнения регрессии в целом
F-тест (тест Фишера) состоит в проверке
гипотезы H0 о статистической
незначимости уравнения регрессии и показателя тесноты связи
незначимости уравнения регрессии и показателя тесноты связи
Слайд 212. Расчет наблюдаемого значения Фишера и его сравнение с табличным
Для нахождения
табличного значения используем
функцию Excel FРАСПОБР (вероятность;
число степеней свободы «Регрессия»; число степеней
свободы «Остаток»)
функцию Excel FРАСПОБР (вероятность;
число степеней свободы «Регрессия»; число степеней
свободы «Остаток»)
Слайд 23Оценка значимости отдельных параметров уравнения регрессии
T-тест (тест Стьюдента) состоит в проверке
гипотезы Н0 о статистической
незначимости коэффициентов регрессии и корреляции
незначимости коэффициентов регрессии и корреляции
Слайд 262. Расчет наблюдаемого значения Стьюдента и его сравнение с табличным
Для нахождения
табличного значения используем
функцию Excel СТЬЮДРАСПОБР (вероятность;
число степеней свободы «Остаток»)
функцию Excel СТЬЮДРАСПОБР (вероятность;
число степеней свободы «Остаток»)
Слайд 27Доверительные интервалы коэффициентов теоретического уравнения регрессии
3. Расчет доверительных интервалов для параметров
регрессии. Интервалы прогноза по линейному уравнению регрессии.
Слайд 29Предсказание среднего значения зависимой переменной
По уравнению регрессии определяется прогнозное значение зависимой
переменной Yx путем подстановки в уравнение прогнозного значения Xp.
Точечный прогноз дополняется интервальной оценкой прогноза Yx.
Слайд 30Предсказание индивидуальных значений зависимой переменной
myxp – стандартная ошибка точечного прогноза
S2 –
остаточная дисперсия на одну степень свободы
t – СВ, имеющая распределение Стьюдента с заданной вероятностью.
t – СВ, имеющая распределение Стьюдента с заданной вероятностью.
Слайд 32Результат применения инструмента «Регрессия»
линейный коэффициент корреляции
коэффициент детерминации
суммы квадратов отклонений
дисперсии на одну
степень свободы
статистика Фишера
статистика Фишера
свободный коэффициент, коэффициент регрессии,
ma, mb, статистика Стьюдента, границы доверительных интервалов
Слайд 36
Индекс корреляции
Для измерения тесноты связи между переменными в нелинейных регрессиях применяется
индекс корреляции
Слайд 38Замена переменных заключается в замене
нелинейных объясняющих переменных новыми
линейными переменными
и сведении
нелинейной регрессии к линейной
нелинейной регрессии к линейной
Полиномиальная модель
Слайд 40Кривая Филлипса (равносторонняя гипербола)
х- норма безработицы,
y – процент прироста заработной
платы
Слайд 42Полулогарифмические модели
Такие модели обычно используются в тех случаях, когда
необходимо исследовать
зависимость темпа роста или
прироста экономических показателей:
прирост объема выпуска от процентного увеличения
затрат ресурсов;
прирост бюджетного дефицита от темпа роста ВНП;
темп роста инфляции от объема денежной массы.
прироста экономических показателей:
прирост объема выпуска от процентного увеличения
затрат ресурсов;
прирост бюджетного дефицита от темпа роста ВНП;
темп роста инфляции от объема денежной массы.
Слайд 43Используется обычно в тех случаях, когда необходимо
исследовать , как процентное
изменение независимой
переменной влияет на абсолютное изменение зависимой
переменной:
влияние относительного (процентного) увеличения
денежной массы на абсолютное изменение ВНП
переменной влияет на абсолютное изменение зависимой
переменной:
влияние относительного (процентного) увеличения
денежной массы на абсолютное изменение ВНП
Слайд 44Логарифмирование обеих частей уравнения
применяется обычно, когда мультипликативную модель
необходимо
привести к линейному виду.
Степенные модели
Слайд 45К классу степенных функций относятся:
кривые спроса и предложения,
производственная функция Кобба-Дугласа,
кривые
освоения для характеристики связи между трудоемкостью продукции и масштабами производства в период освоения и выпуска нового вида изделий,
зависимость валового национального дохода от уровня занятости.
зависимость валового национального дохода от уровня занятости.
Слайд 46Показательные (экспоненциальные) модели
Широкий класс экономических показателей характеризуется
приблизительно постоянным темпом относительного
прироста во времени. Этому соответствует следующая
форма зависимости показателя Y от времени X:
форма зависимости показателя Y от времени X:
Слайд 48Логистическая кривая
Применяется для описания поведения показателей,
имеющих определенные «уровни насыщения»:
зависимость спроса
на товар Y от дохода X,
развитие производства новых товаров,
рост численности населения (впервые применил
А. Кетле (1796-1874))
развитие производства новых товаров,
рост численности населения (впервые применил
А. Кетле (1796-1874))
Слайд 49Логлинейная модель
Используется в банковском и финансовом анализе.
Y0 – начальная величина
переменной Y (первоначальная сумма вклада), r – сложный темп прироста величины Y
(процентная ставка); Yt – значение величины Y в момент
времени t (вклад в банке в момент времени t).
(процентная ставка); Yt – значение величины Y в момент
времени t (вклад в банке в момент времени t).
Слайд 50Коэффициент эластичности
Величина коэффициента эластичности показывает, на сколько процентов изменится результативный признак
Y, если факторный признак изменится на 1 %.
Средний показатель эластичности:
