университет имени Н.Э.Баумана
2015г.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Начертательная геометрия. Пересечение поверхностей презентация
Содержание
- 1. Начертательная геометрия. Пересечение поверхностей
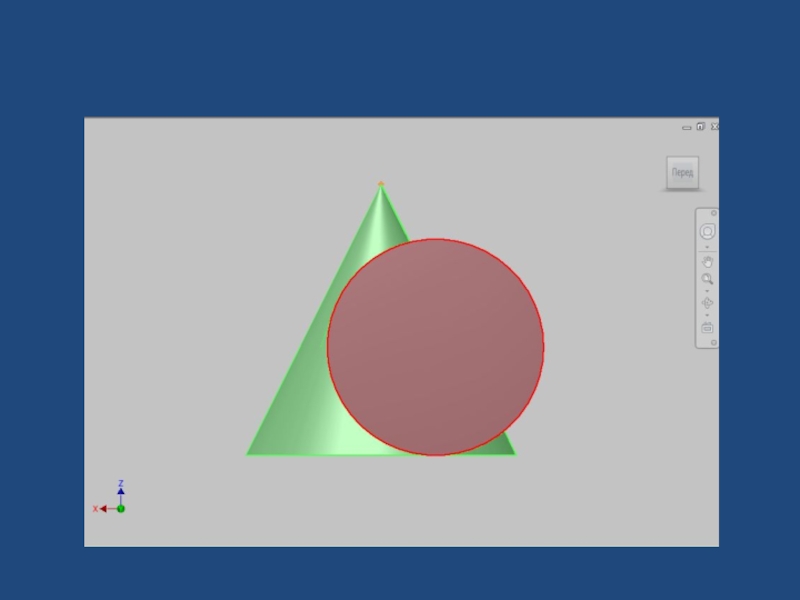
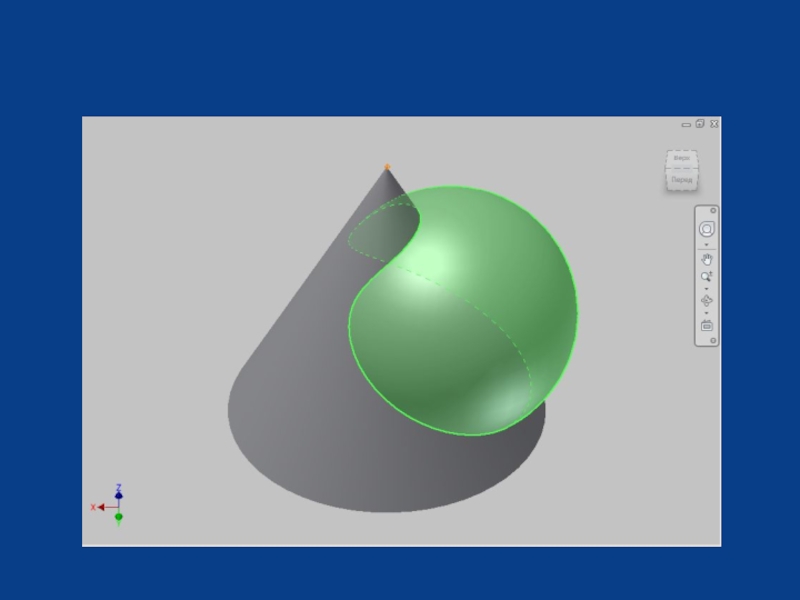
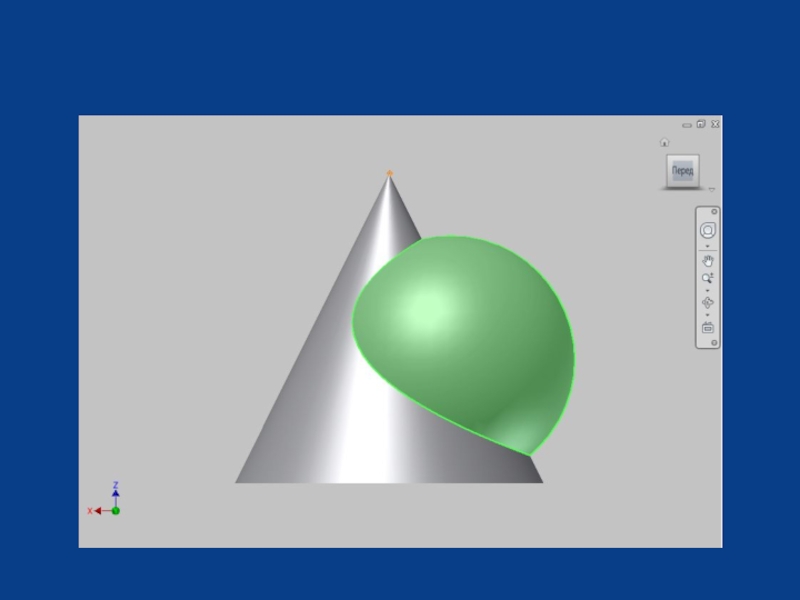
- 2. Задача 73a. Построить проекции линий пересечения заданных поверхностей.
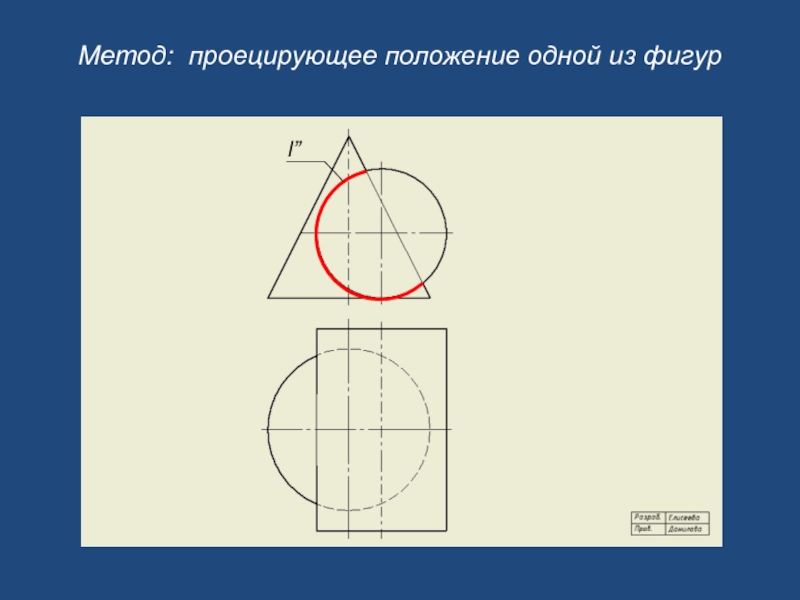
- 7. Метод: проецирующее положение одной из фигур l”
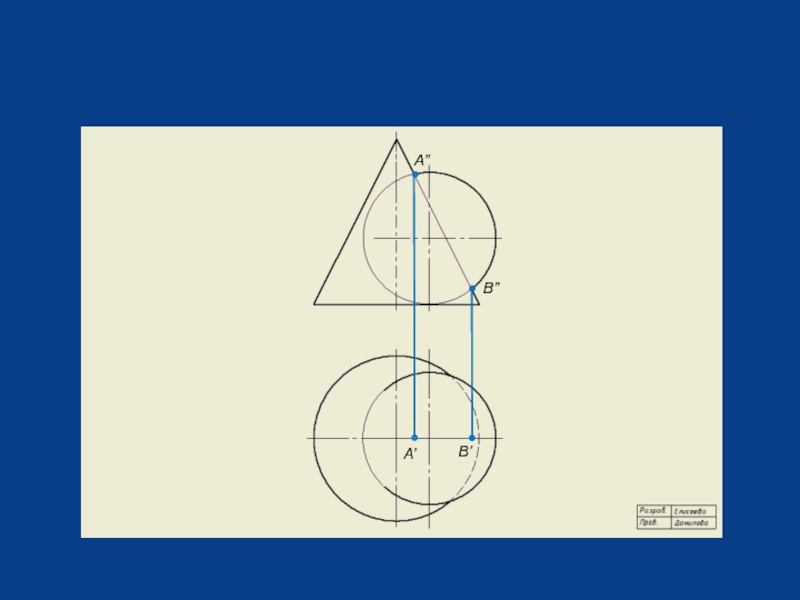
- 8. А”
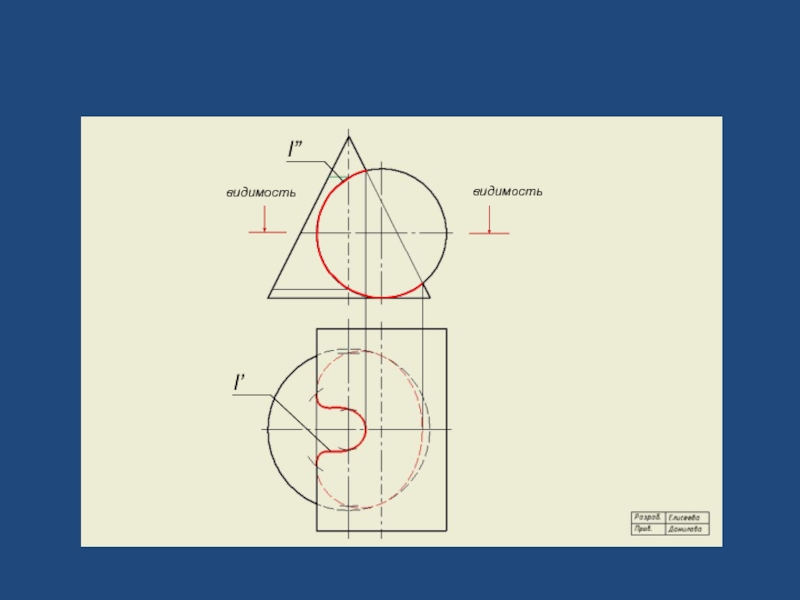
- 9. видимость видимость l” l’
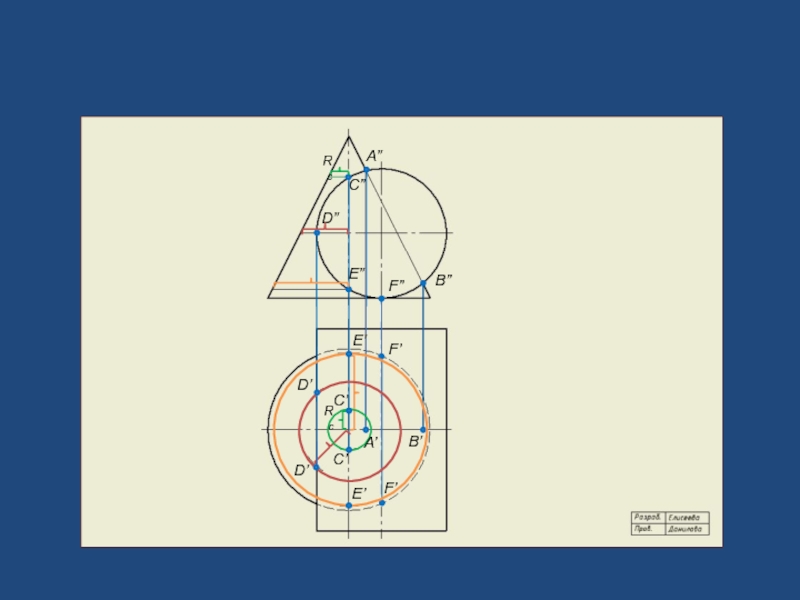
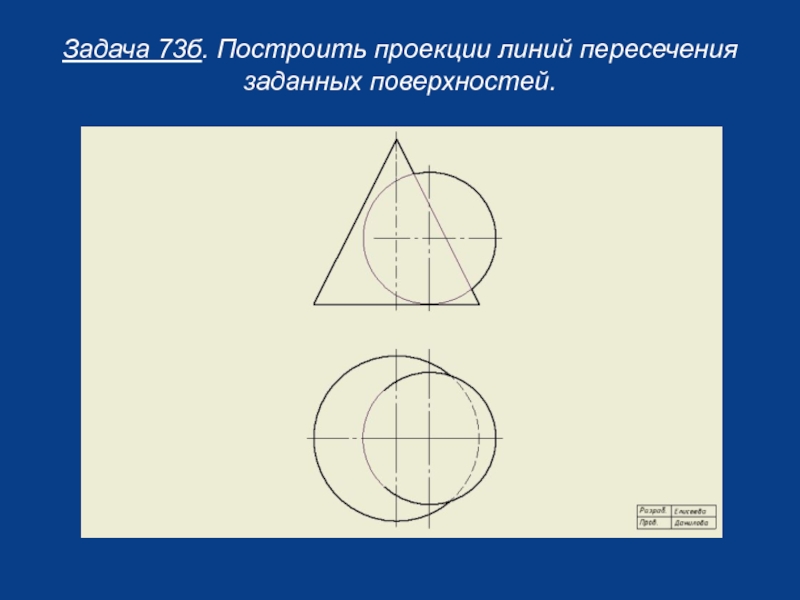
- 11. Задача 73б. Построить проекции линий пересечения заданных поверхностей.
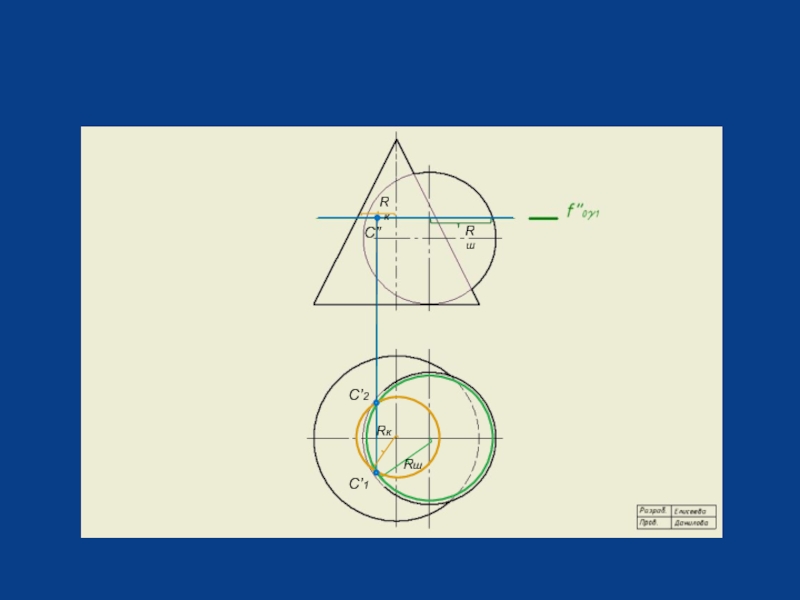
- 15. Метод секущих параллельных плоскостей
- 16. Метод секущих параллельных плоскостей
- 17. Метод секущих параллельных плоскостей
- 18. А” B” А’ B’
- 19. C’1 C’2
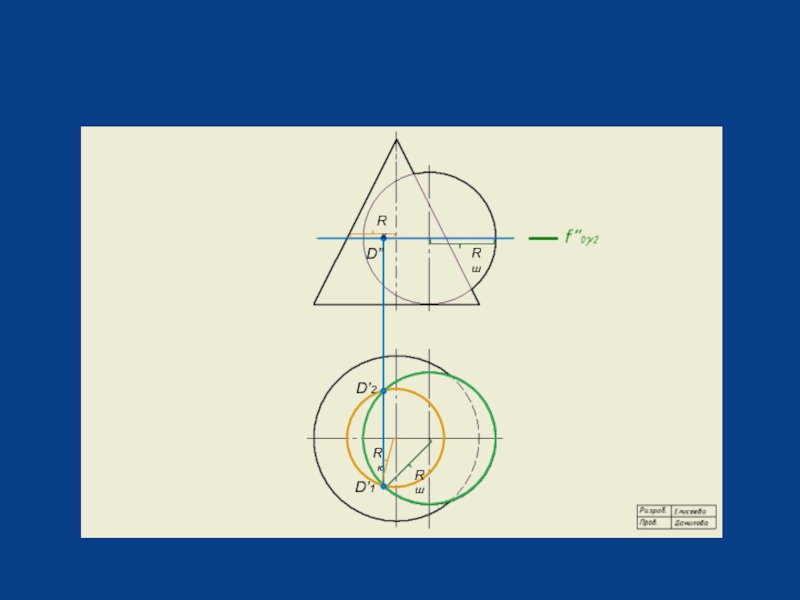
- 20. D’1 Rк
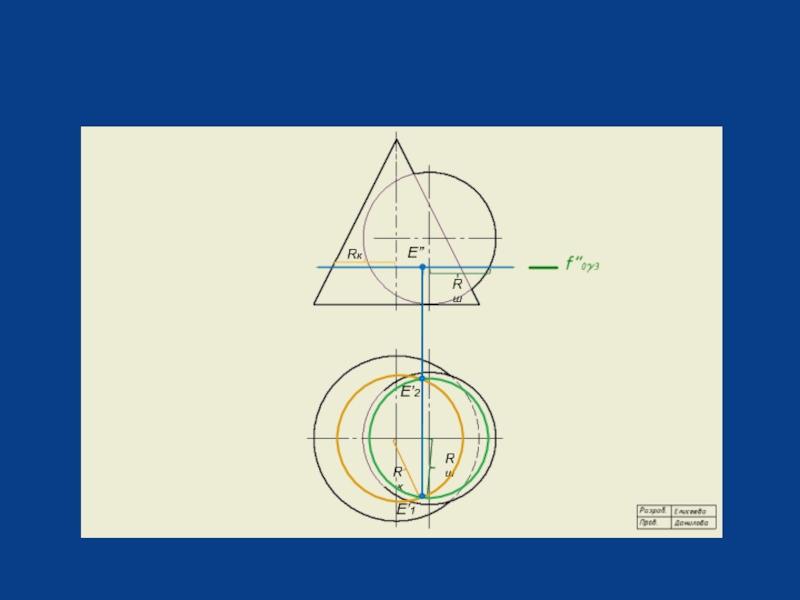
- 21. E” Rк
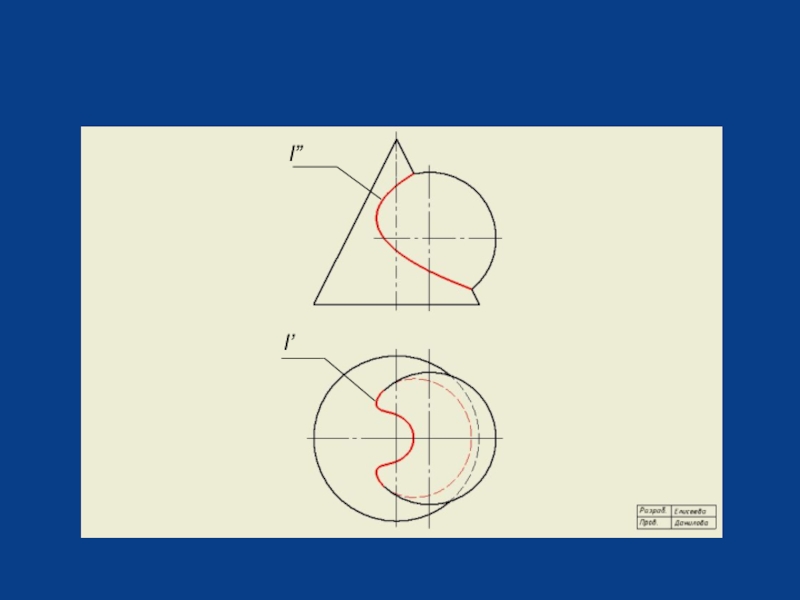
- 22. l” l’
- 23. Задача 74-3. Построить проекции линии пересечения поверхностей
- 24. 1. Задаем линию пересечения цилиндра с будущей
- 25. Задача 74-3. Построить проекции линии пересечения поверхностей
- 29. Задача 74-3. Построить проекции линии пересечения поверхностей
Задача 73a. Построить проекции линий пересечения заданных поверхностей.
Слайд 1Начертательная геометрия Семинар №11 Пересечение поверхностей. Подготовили: Данилова У.Б., Елисеева О.И. Московский государственный технический
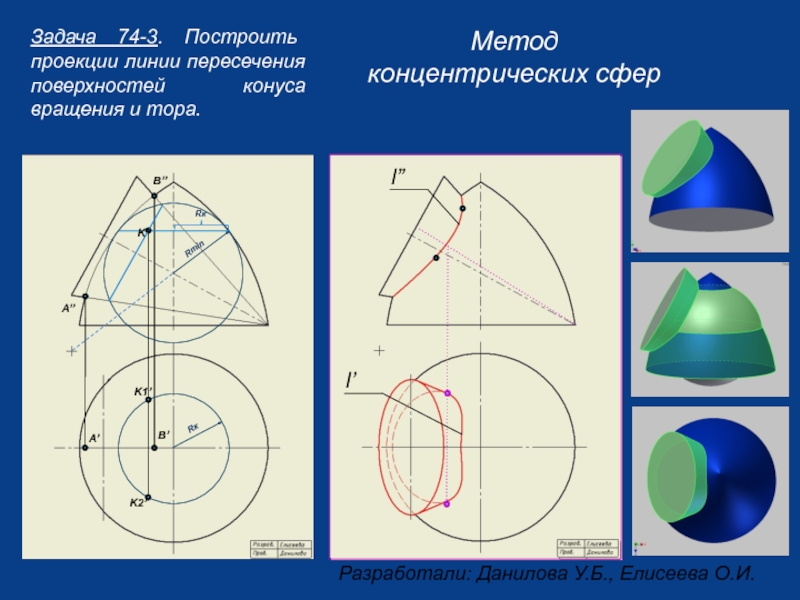
Слайд 23Задача 74-3. Построить проекции линии пересечения поверхностей конуса вращения и тора.
А’’
В’’
А’
В’
Rmin
K”
Rк
Rк
K1’
K2’
M1”
M2”
M1’
M1’
RM2
RM1
RM1
RM2
M2’
M2’
Метод концентрических сфер
l”
l’
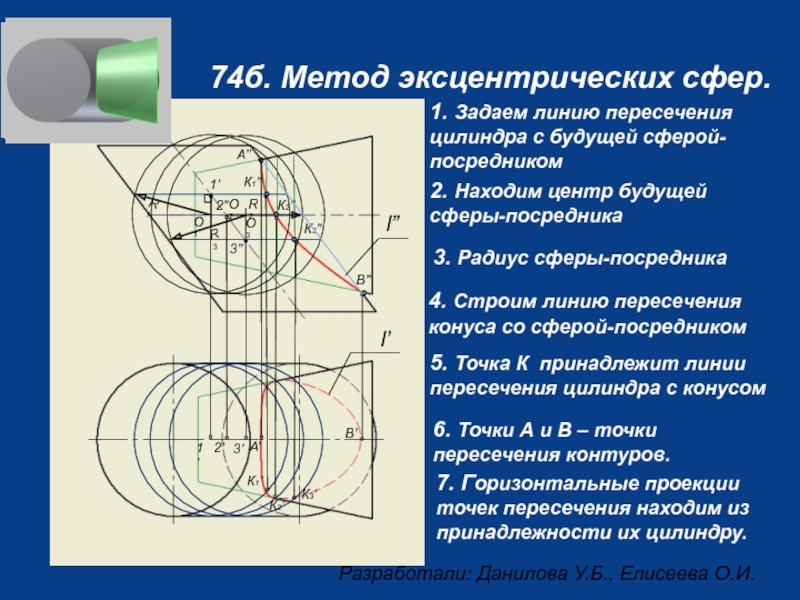
Слайд 241. Задаем линию пересечения цилиндра с будущей сферой-посредником
R1
О1
2. Находим центр будущей
сферы-посредника
3. Радиус сферы-посредника
4. Строим линию пересечения конуса со сферой-посредником
5. Точка К принадлежит линии пересечения цилиндра с конусом
К1’’
О3
R3
R2
О2
К2’’
К3’’
A’’
В’’
А’
В’
1’’
К3’
К2’
К1’
1’
2’
3’
6. Точки А и В – точки пересечения контуров.
7. Горизонтальные проекции точек пересечения находим из принадлежности их цилиндру.
74б. Метод эксцентрических сфер.
2’’
3’’
l”
l’
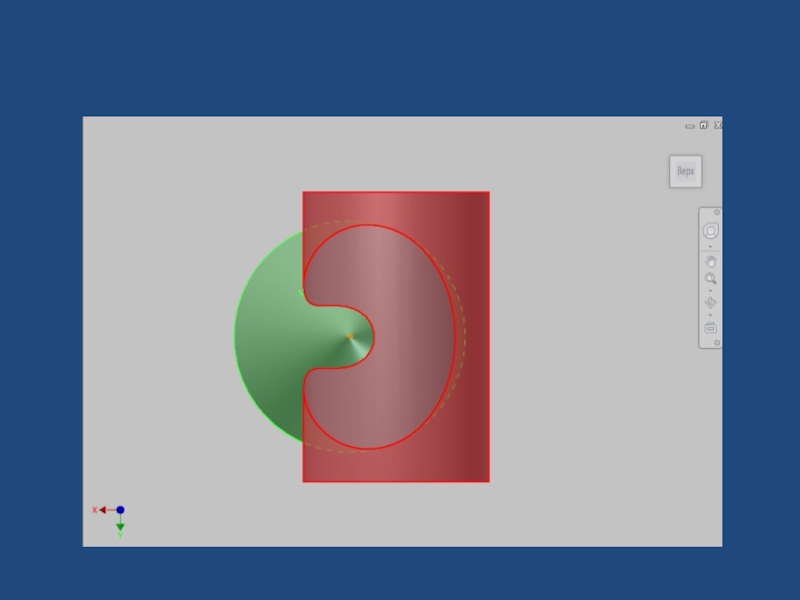
Слайд 25Задача 74-3. Построить проекции линии пересечения поверхностей конуса вращения и цилиндра
вращения.
Теорема Монжа .
Если две поверхности второго порядка описаны около третьей поверхности или вписаны в нее, то линия их пересечения распадается на две плоские кривые второго порядка. Плоскости этих кривых проходят через прямую, соединяющую точки линий касания.
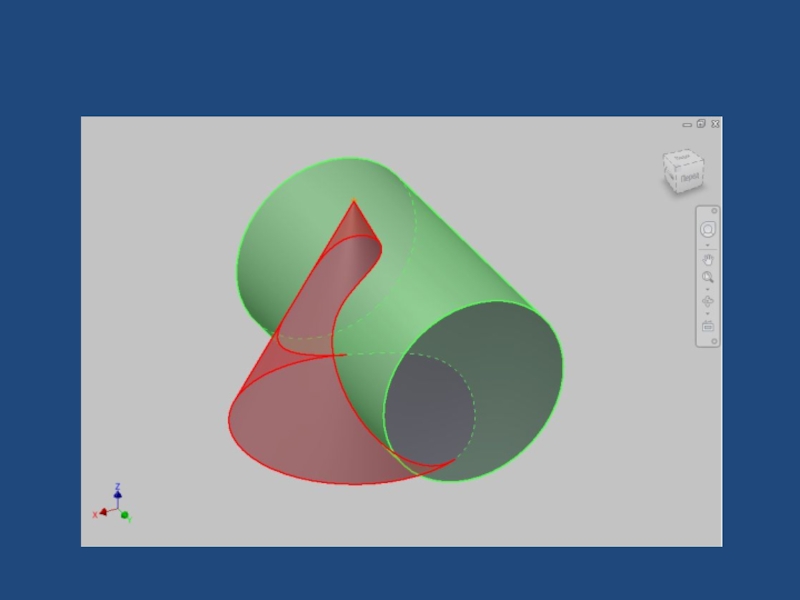
Слайд 29Задача 74-3. Построить проекции линии пересечения поверхностей конуса вращения и цилиндра
вращения.
Точки А, В, С и D – пересечения контуров.
Точка К – пересечения двух касательных: сферы с конусом и сферы с цилиндром.
Точки G F принадлежат линии видимости –горизонтальной очерковой цилиндра.
Линии A’G’ K’ C’, B’K’F’D’– эллипсы.
А’’
В’’
C’’
D’’
K’’
G’’
F’’
А’
В’
С’
D’
F’
F’
G’
G’
K’
K’
l1”
l2”
l1’
l2’
