- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Мультиколлинеарность презентация
Содержание
- 1. Мультиколлинеарность
- 2. Цели лекции 1. Объяснить сущность проблемы мультиколлинеарности
- 3. Коллинеарность и мультиколлинеарность Термин «коллинеарность» характеризует линейную
- 4. Виды мультиколлинеарности. Строгая и нестрогая мультиколлинеарность 1.
- 5. Суть строгой мультиколлинеарности Связь между объясняющими переменными – функциональная
- 6. Суть строгой мультиколлинеарности. Выводы Строгая мультиколлинеарность
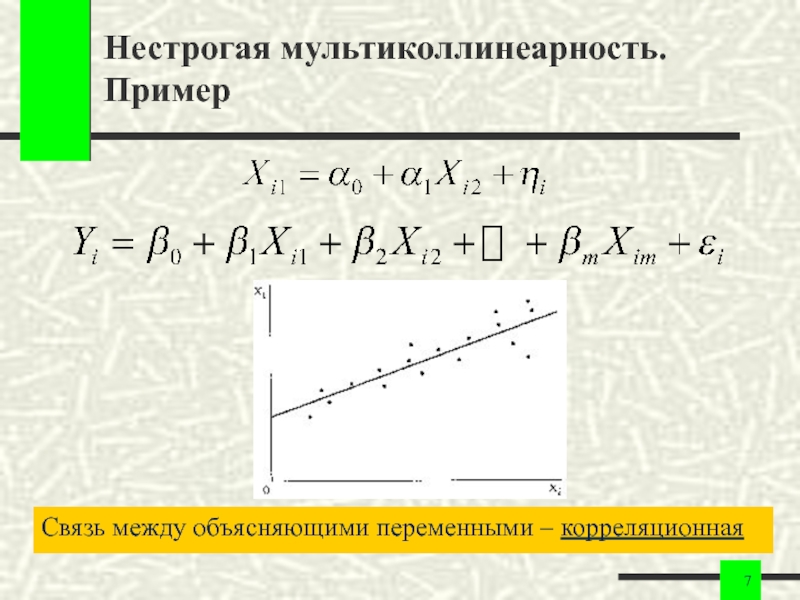
- 7. Нестрогая мультиколлинеарность. Пример Связь между объясняющими переменными – корреляционная
- 8. Сложность проблемы мультиколлинеарности 1. Корреляционные связи есть
- 9. Причины возникновения мультиколлинеарности 1. Ошибочное включение в
- 10. Мультиколлинеарность как результат логической ошибки Ошибочное признание независимыми содержательно зависимых переменных: Оценка коэффициентов уравнения невозможна!
- 11. Мультиколлинеарность из-за доминантной переменной Доминантная переменная «забивает» влияние остальных: Влияние остальных переменных становится незначимым
- 12. Неизбежность мультиколлинеарности 1. Мультиколлинеарность – нормальное явление.
- 13. Механизм действия мультиколлинеарности Мультиколлинеарность проявляется в совместном
- 14. Зависимость мультиколлинеарности от выборки Мультиколлинеарность – явление,
- 15. Зависимость мультиколлинеарности от смысла задачи Мультиколлинеарность может
- 16. Истинная мультиколлинеарность при отсутствии парных зависимостей Пример.
- 17. Последствия мультиколлинеарности: диагноз и прогноз 1. Оценки
- 18. Последствия мультиколлинеарности: диагноз и прогноз 5. Численная
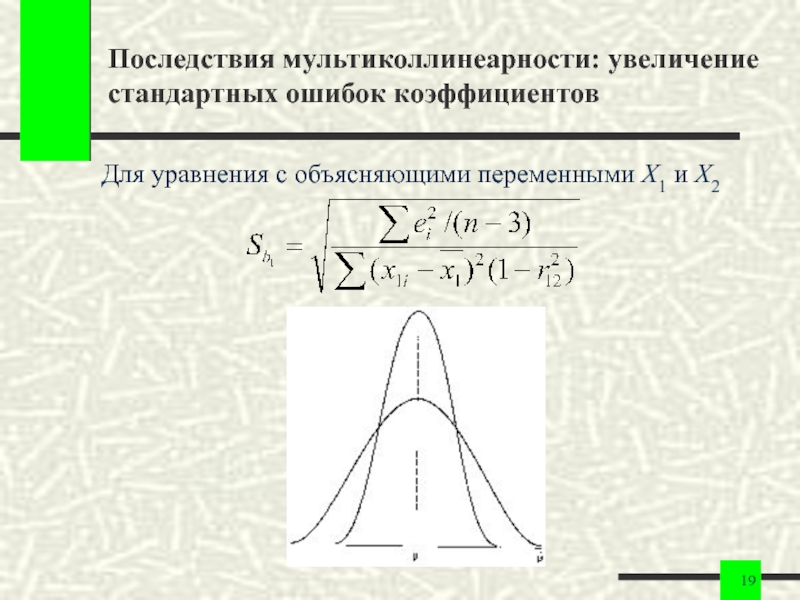
- 19. Последствия мультиколлинеарности: увеличение стандартных ошибок коэффициентов Для уравнения с объясняющими переменными X1 и X2
- 20. Последствия мультиколлинеарности: увеличение стандартных ошибок коэффициентов Практически
- 21. Обнаружение мультиколлинеарности. Основной признак Внешним признаком наличия
- 22. Обнаружение мультиколлинеарности. Дополнительные признаки 1. Высокие R2
- 23. Фактор инфляции вариации как оценка эффекта мультиколлинеарности
- 24. Методы устранения мультиколлинеарности 1. Изменить или увеличить
- 25. Устранение мультиколлинеарности. Преобразование переменных Пусть эмпирическое уравнение
- 26. Конец лекции
Слайд 2Цели лекции
1. Объяснить сущность проблемы
мультиколлинеарности
2. Изучить последствия мультиколлинеарности
3. Указать средства обнаружения
мультиколлинеарности
4.
с мультиколлинеарностью
Слайд 3Коллинеарность и мультиколлинеарность
Термин «коллинеарность» характеризует линейную
связь между двумя объясняющими переменными.
«Мультиколлинеарность» означает
связь между более чем двумя объясняющими
переменными.
На практике всегда используется один термин –
мультиколлинеарность.
Термин «мультиколлинеарность» введен Рагнаром Фришем
Слайд 4Виды мультиколлинеарности. Строгая и нестрогая мультиколлинеарность
1. Строгая мультиколлинеарность – наличие
линейной функциональной
объясняющими переменными (иногда также и
зависимой).
2. Нестрогая мультиколлинеарность – наличие
сильной линейной корреляционной связи между
между объясняющими переменными (иногда также и
зависимой).
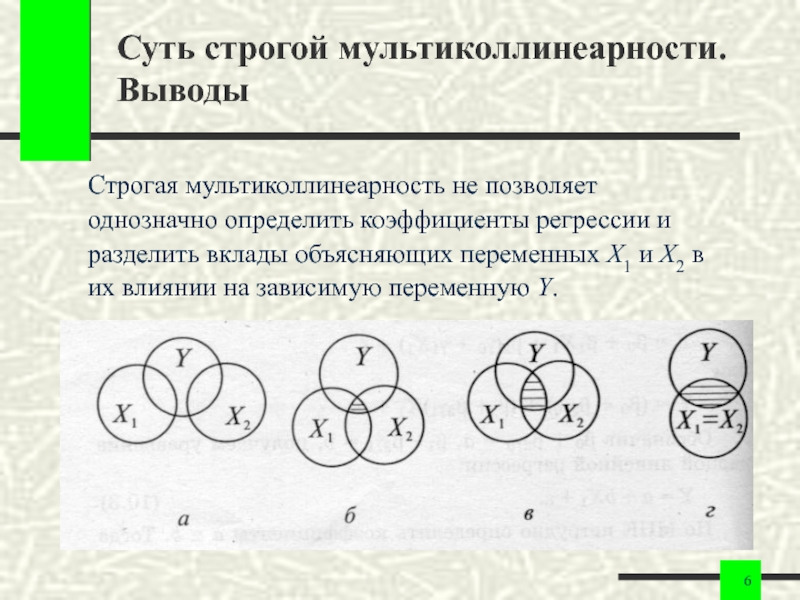
Слайд 6Суть строгой мультиколлинеарности. Выводы
Строгая мультиколлинеарность не позволяет
однозначно определить коэффициенты регрессии и
разделить
их влиянии на зависимую переменную Y.
Слайд 8Сложность проблемы мультиколлинеарности
1. Корреляционные связи есть всегда. Проблема
мультиколлинеарности – сила проявления
корреляционных
2. Однозначных критериев мультиколлинеарности не
существует.
3. Строгая мультиколлинеарность нарушает предпосылку 50
теоремы Гаусса-Маркова и делает построение регрессии
невозможным. (Согласно теоремы Кронекера-Капелли
система уравнений имеет бесчисленное множество решений).
4. Нестрогая мультиколлинеарность затрудняет работу, но не
препятствует получению правильных выводов.
Слайд 9Причины возникновения мультиколлинеарности
1. Ошибочное включение в уравнение регрессии двух
или более линейно
2. Две (или более) объясняющих переменных, в
нормальной ситуации слабо коррелированные,
становятся в конкретной выборке сильно
коррелированными.
3. В модель включается объясняющая переменная,
сильно коррелирующая с зависимой переменной (такая
переменная называется доминантной).
Слайд 10Мультиколлинеарность как результат логической ошибки
Ошибочное признание независимыми
содержательно зависимых переменных:
Оценка коэффициентов уравнения
Слайд 11Мультиколлинеарность из-за доминантной переменной
Доминантная переменная «забивает»
влияние остальных:
Влияние остальных переменных становится незначимым
Слайд 12Неизбежность мультиколлинеарности
1. Мультиколлинеарность – нормальное явление.
Практически любая модель содержит
мультиколлинеарность.
2. Мы не
мультиколлинеарность до появления явных
симптомов.
3. Только чрезмерно сильные связи становятся
помехой.
Слайд 13Механизм действия мультиколлинеарности
Мультиколлинеарность проявляется в совместном
действии факторов:
1. Построить модель – значит
каждого фактора.
2. Если два или более фактора изменяются только
совместно, их вклад по отдельности становится
невозможно различить.
3. Чем более сильно коррелированы переменные,
тем труднее различить их вклад.
Слайд 14Зависимость мультиколлинеарности от выборки
Мультиколлинеарность – явление, проявляющееся на уровне выборки:
1. В
быть сильной, в другой слабой.
2. Выборочные данные следует предварительно
всесторонне исследовать.
3. Полезен расчет выборочных коэффициентов
корреляции, ковариационной матрицы и ее
определителя.
Слайд 15Зависимость мультиколлинеарности от смысла задачи
Мультиколлинеарность может быть выявлена при
содержательном анализе задачи
При строгом контроле за ценами в некоторый период возникает строгая мультиколлинеарность
Пример. Номинальная (in) и реальная величина (ir) процента (inf – темп инфляции)
Слайд 16Истинная мультиколлинеарность при отсутствии парных зависимостей
Пример. Рассмотрим три ряда данных:
В данной
но
Слайд 17Последствия мультиколлинеарности: диагноз и прогноз
1. Оценки коэффициентов остаются несмещенными.
2. Стандартные ошибки
увеличиваются.
3. Вычисленные t-статистики занижены.
4. Неустойчивость оценок. Добавление или
исключение малого количества информации
(например, только одного наблюдения) может
привести к очень сильному изменению оценок
коэффициентов. При этом резко уменьшается и
точность предсказания по модели.
Слайд 18Последствия мультиколлинеарности: диагноз и прогноз
5. Численная неустойчивость процедуры оценивания,
вызванная ошибками машинного
накоплением этих ошибок.
6. Высокая коррелированность коэффициентов лишает
смысла их интерпретацию.
7. Общее качество уравнения, а также оценки
переменных, не связанных мультиколлинеарностью,
Остаются незатронутыми.
8. Чем ближе мультиколлинеарность к строгой
(совершенной), тем серьезнее ее последствия.
Слайд 19Последствия мультиколлинеарности: увеличение стандартных ошибок коэффициентов
Для уравнения с объясняющими переменными X1
Слайд 20Последствия мультиколлинеарности: увеличение стандартных ошибок коэффициентов
Практически отсюда следует возможность получить
незначимый коэффициент
Типичная ситуация.
1. Оба коэффициента в теоретической модели положительны.
2. Оба парных коэффициента корреляции между объясняющими и зависимой переменной положительны.
3. Парный коэффициент корреляции между объясняющими переменными положителен, причем корреляция между ними сильнее, чем у каждой с зависимой переменной.
В этой ситуации у одного из коэффициентов практически всегда «неправильный» знак
Слайд 21Обнаружение мультиколлинеарности. Основной признак
Внешним признаком наличия мультиколлинеарности служат
слишком большие значения элементов
Основной признак мультиколлинеарности: определитель
корреляционной матрицы R близок к нулю:
Если все объясняющие переменные не коррелированы между собой,
то . В противном случае .
Слайд 22Обнаружение мультиколлинеарности. Дополнительные признаки
1. Высокие R2 и F-статистика, но некоторые (или
коэффициенты незначимы, т.е. имеют низкие t-статистики.
2. Высокие парные коэффициенты корреляции.
3. Высокие частные коэффициенты корреляции.
4. Высокие значения коэффициента VIF («фактор инфляции
вариации»).
5. Знаки коэффициентов регрессии противоположны
ожидаемым.
6. Добавление или удаление наблюдений из выборки сильно
изменяют значения оценок.
Слайд 23Фактор инфляции вариации как оценка эффекта мультиколлинеарности
Если VIF > 10, то
считаются мультиколлинеарными.
Слайд 24Методы устранения мультиколлинеарности
1. Изменить или увеличить выборку.
2. Исключить из модели одну
3. Преобразовать мультиколлинеарные переменные:
- использовать нелинейные формы;
- использовать агрегаты (линейные комбинации переменных);
- использовать первые разности вместо самих переменных.
4. Использовать при оценке коэффициентов метод главных
компонент или другие специальные процедуры расчета
коэффициентов при плохой обусловленности .
5. Ничего не делать!
Самое главное – выбрать правильное средство
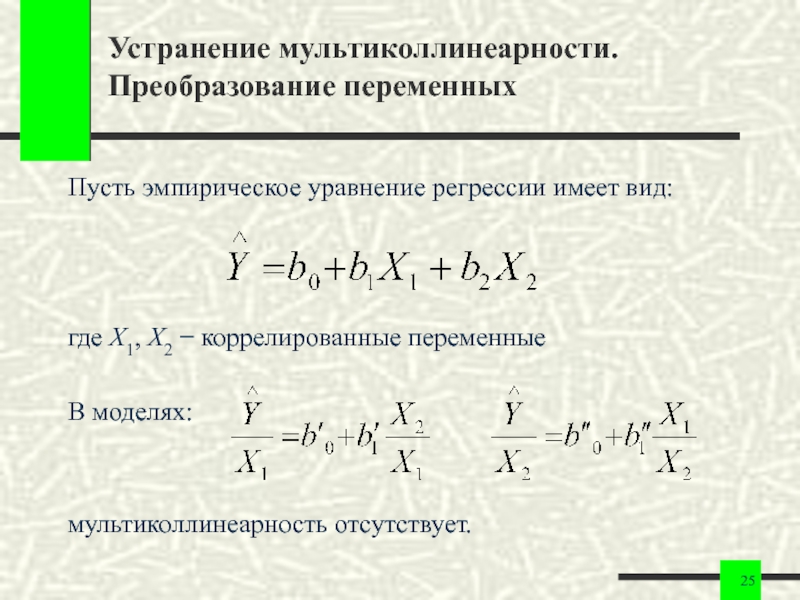
Слайд 25Устранение мультиколлинеарности. Преобразование переменных
Пусть эмпирическое уравнение регрессии имеет вид:
где X1, X2
В моделях:
мультиколлинеарность отсутствует.