- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Моделирование выборочных данных суммой экспоненциальных функций Лекция 12 презентация
Содержание
- 1. Моделирование выборочных данных суммой экспоненциальных функций Лекция 12
- 2. DSP Моделирование выборочных данных суммой экспоненциальных функций
- 3. DSP Цифровой спектральный анализ Введение
- 4. DSP
- 5. DSP
- 6. DSP
- 7. DSP
- 8. DSP
- 9. DSP
- 10. DSP
- 11. DSP
- 12. DSP
- 13. DSP
- 14. DSP
- 15. DSP
- 16. DSP
- 17. DSP Цифровой спектральный анализ
- 18. DSP Цифровой спектральный анализ
- 19. DSP Цифровой спектральный анализ
- 20. DSP Цифровой спектральный анализ
- 21. DSP Цифровой спектральный анализ
- 22. DSP Цифровой спектральный анализ Рисунок 34.
- 23. DSP Цифровой спектральный анализ
- 24. DSP Цифровой спектральный анализ
- 25. DSP Цифровой спектральный анализ Рисунок 37.
Слайд 2DSP
Моделирование выборочных данных суммой экспоненциальных функций
(метод Прони)
Введение
Метод
Модифицированный метод наименьших квадратов Прони
Спектральная интерпретация метода Прони
Примеры спектральных оценок на основе метода Прони
Слайд 3DSP
Цифровой спектральный анализ
Введение
Метод Прони — это метод моделирования последовательности отсчетов
Слайд 4DSP
Цифровой спектральный анализ
Метод Прони, строго говоря, не является методом спектрального оценивания.
Заметим, что периодограммную оценку спектральной плотности мощности (СПМ) можно считать эквивалентной среднеквадратичной аппроксимации данных с помощью ряда Фурье, т.е. гармонического набора комплексных синусоид. Так для N отсчетов данных x[0],…,x[N–1], разделенных интервалом T, аппроксимирующая последовательность имеет вид
где
если коэффициенты am определяются из условия минимизации суммарной среднеквадратичной ошибки аппроксимации
а частоты fm гармонически связаны между собой:
Слайд 5DSP
Цифровой спектральный анализ
Таким образом, в гармонической модели частоты и число синусоид
соответствующего вычислению СПМ дискретной периодограммы.
В свою очередь, негармоническая модель, используемая в методе Прони, требует оценки не только мощности, но и числа синусоид и их частот.
С другой стороны, гармоническая модель наблюдаемых данных предполагает их периодическое продолжение вне интервала наблюдения, что далеко не всегда соответствует реальному поведению процесса и связано с отрицательным проявлением эффектов окна. В негармонической модели Прони искажающее действие окна исключено, поэтому точность оценки СПМ по сравнению со стандартным подходом на основе преобразования Фурье может значительно улучшиться.
Слайд 6DSP
Цифровой спектральный анализ
Метод наименьших квадратов Прони
Предположим, что имеется N комплексных
(6.66)
где
Заметим, что hk – это комплексная амплитуда, представляющая собой независящий от времени параметр, а zk – это комплексная экспонента, которая описывает параметр, зависящий от времени.
Отыскание параметров Ak, fk, Θk, ak и r, минимизирующих сумму квадратов ошибок
где
представляет трудную нелинейную задачу аппроксимации по методу наименьших квадратов. Для ее решения могут быть использованы различные итеративные алгоритмы, требующие больших вычислительных затрат и не всегда сходящиеся к глобальному минимуму. Альтернативное субоптимальное решение, в котором используются решения двух систем линейных уравнений, основано на методе наименьших квадратов Прони.
Слайд 7DSP
Цифровой спектральный анализ
Ключевым моментом метода Прони является тот факт, что функция
(6.67)
для которого справедливо эквивалентное представление в виде степенного ряда
(6.68)
с комплексными коэффициентами a(m), для которых a(0)=1. Осуществляя в выражении (6.66) сдвиг индекса от n до n–m и домножая обе его части на коэффициент a(m), получим
где .
Записывая аналогичные произведения a[0] ,…, и суммируя p+1 произведение, получаем
, (6.69)
где .
Слайд 8DSP
Цифровой спектральный анализ
Осуществляя в (6.66) подстановку
получим уравнение
(6.70)
в котором равенство нулю
(6.71)
определенное для .
Полином Φ(z), ассоциированный с этим разностным уравнением, называют характеристическим, а его корни zk определяют экспоненциальные параметры в (6.66).
Если учесть, что разность между реальными измеренными данными x[n] и их аппроксимацией есть величина ошибки ε[n], так, что
(6.72)
то подстановка (6.72) в (6.71) дает соотношение
(6.73)
где использовано равенство и положено a[0]=1.
Слайд 9DSP
Цифровой спектральный анализ
Соотношение (6.73) можно трактовать как моделирующее процесс x[n] с
В обобщенном методе Прони вводится новая ошибка
(6.74)
и моделирующее x[n] уравнение принимает вид
(6.75)
который идентичен уравнению для ошибки линейного предсказания вперед e[n] с коэффициентами фильтра линейного предсказания a[m].
Выбирая параметры a[m] из условия минимизации суммы квадратов
ошибок линейного предсказания , мы тем самым сводим
нелинейную задачу минимизации суммы квадратов ошибок аппроксимации
, к линейной системе нормальных ковариационных
уравнений линейного предсказания.
Таким образом, первый этап обобщенной процедуры Прони сводится к процедуре оценивания АР–параметров a[m] на основе ковариационного метода линейного предсказания с оценкой числа экспонент p по правилам выбора порядка АР–модели.
Слайд 10DSP
Цифровой спектральный анализ
Второй этап процедуры состоит в нахождении корней zi полинома
Наконец, когда значения параметров были определены с помощью линейного предсказания по методу наименьших квадратов и факторизацией полинома, то аппроксимация , описываемая уравнением (6.66), становится линейной относительно оставшихся неизвестных параметров . Матричная форма соотношения (6.66) имеет вид
(6.76)
где (N × p) матрица Z, (p × 1) вектор H и (N × 1) вектор определяются выражениями:
(6.77)
Слайд 11DSP
Цифровой спектральный анализ
Минимизируя сумму квадратов ошибок
hk,получаем следующее комплексное нормальное уравнение для их определения
(6.78)
где (p × p) матрица и (N × 1) вектор отсчетов данных определяются выражениями
(6.79)
Система уравнений (6.79) решается относительно неизвестных параметров hk, например, по методу Холецкого.
По найденным параметрам zi и hi находятся коэффициенты затухания αi, частоты fi, амплитуды Ai и начальные фазы Θi с помощью соотношений:
(6.80)
Слайд 12DSP
Цифровой спектральный анализ
Модифицированный метод наименьших квадратов Прони
Для процессов, состоящих из
(6.81)
где , , .
Заметим, что zk являются величинами единичного модуля с произвольными частотами, которые появляются комплексно сопряженными парами до тех пор, пока либо .
Соответствующий (6.67) и (6.68) характеристический полином для этого случая имеет вид
(6.82)
где a[0]=1, а a[k] – вещественные коэффициенты. Поскольку корни полинома (6.82) имеют единичный модуль и появляются в виде комплексно сопряженных пар, то уравнение (6.82) должно быть инвариантным относительно подстановки z -1 вместо z:
(6.83)
Слайд 13DSP
Цифровой спектральный анализ
Сравнивая (6.82) и (6.83) можно видеть, что
(6.84)
для .
С учетом равенства и введением коэффициентов
(6.84) преобразуется в уравнение
(6.85)
Слайд 14DSP
Цифровой спектральный анализ
В модифицированном методе Прони на первом этапе ошибка линейного
определенной на интервале (используются только имеющиеся отсчеты данных), и минимизируется сумма квадратов ошибок сглаживания
Получаемые нормальные уравнения для определения коэффициентов gp[k] соответствуют уравнениям модифицированного ковариационного метода оценки АР–параметров.
Слайд 15DSP
Цифровой спектральный анализ
Спектральная интерпретация метода Прони
Процедура Прони обычно завершается вычислением
Одно из допущений состоит в том, что сумма экспонент дискретного времени в соотношении (6.66) определяется на интервале –∞
(6.86)
Z–преобразование от (6.86) имеет вид
для |z|>|zk|<1 (затухающие экспоненты), спектральная плотность энергии Прони для рассматриваемой модели будет определяться выражением
которое определено на интервале частот .
(6.87)
Слайд 16DSP
Цифровой спектральный анализ
Другим возможным допущением является двусторонняя функция вида
(6.88)
где
и
Такое определение (6.88)
для
Спектральная плотность энергии в этом случае определится как
(6.89)
для
Слайд 17DSP
Цифровой спектральный анализ
В общем случае спектр
Слайд 18DSP
Цифровой спектральный анализ
Примеры спектральных оценок на основе метода Прони На рис.
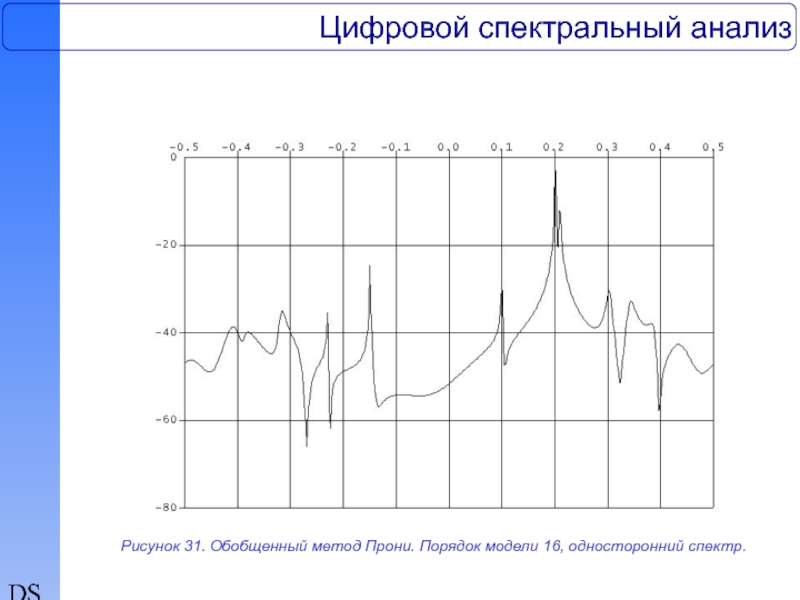
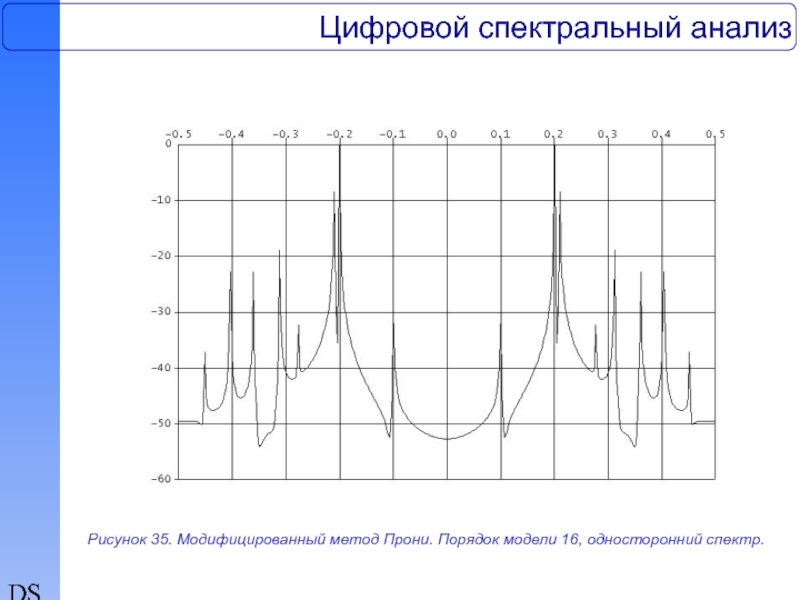
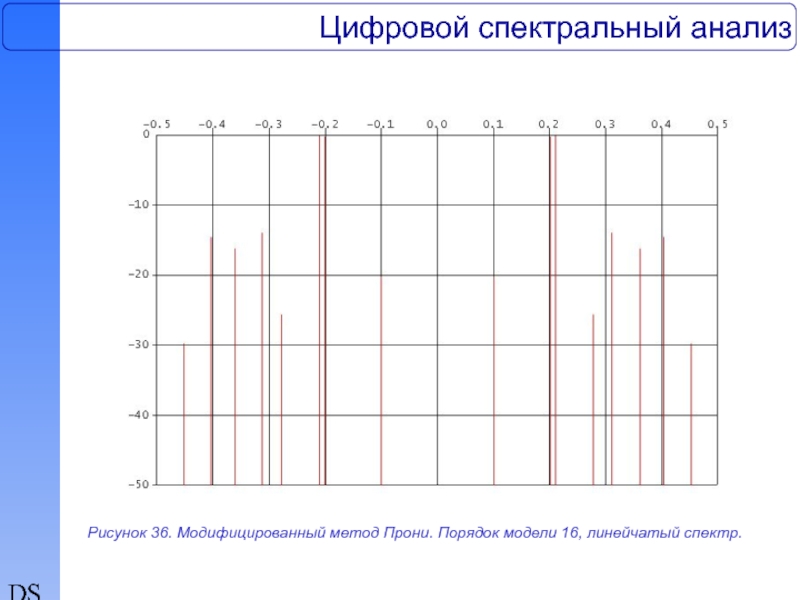
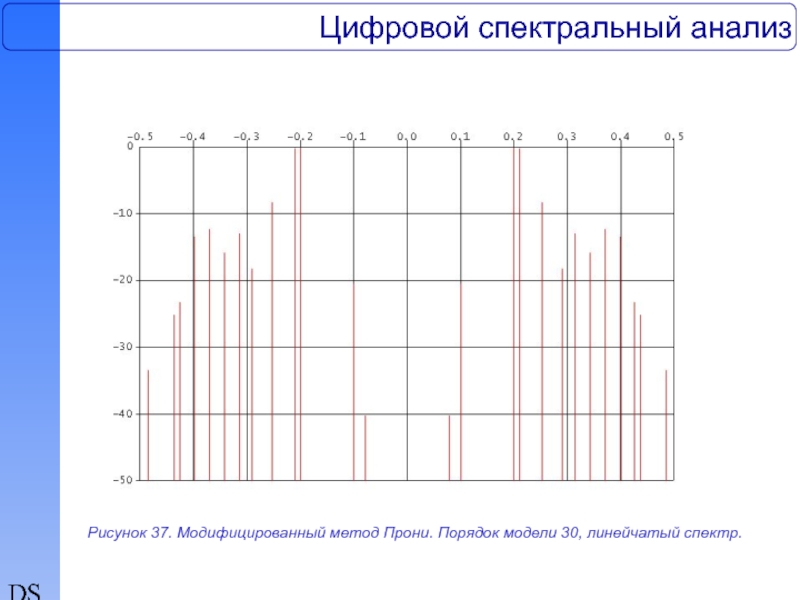
64-точечной тест-последовательности Марпла, полученные на основе обобщенного метода Прони с использованием односторонней и двусторонней моделей при значениях порядка моделей 16 и 30 соответственно. На рис.35-37 представлены спектральные оценки действительной 64-точечной тест-последовательности, полученные на основе модифицированного метода Прони с использованием односторонней модели и линейчатого спектра при значениях порядка моделей 16 и 30 соответственно. Действительная тест-последовательность, содержащая три синусоиды с частотами 0.1, 0.2, и 0.21 при отношении сигнал/шум +10дб, +20дб, +30дб соответственно, где отношение сигнал/шум определяется как отношение мощности каждой синусоиды к полной мощности аддитивного окрашенного шума, полученного фильтрацией белого гауссова шума, заимствована из обзора Кея и Марпла. Полоса шумового процесса центрирована относительно частоты 0.35.
Слайд 19DSP
Цифровой спектральный анализ
Рисунок 31. Обобщенный метод Прони. Порядок модели 16, односторонний
Слайд 20DSP
Цифровой спектральный анализ
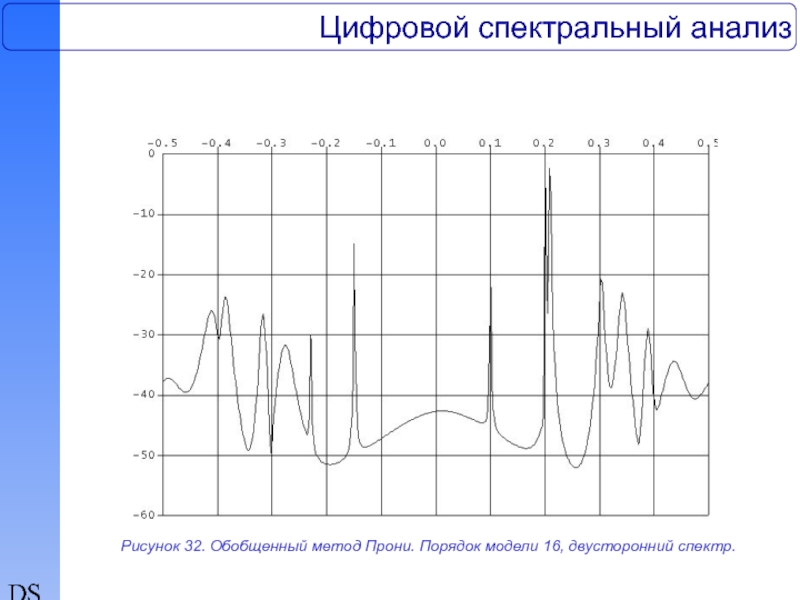
Рисунок 32. Обобщенный метод Прони. Порядок модели 16, двусторонний
Слайд 21DSP
Цифровой спектральный анализ
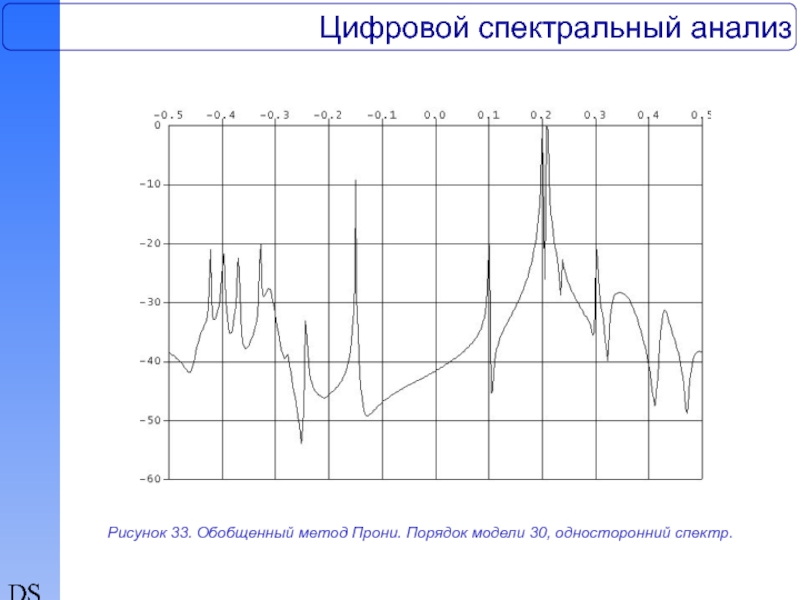
Рисунок 33. Обобщенный метод Прони. Порядок модели 30, односторонний
Слайд 22DSP
Цифровой спектральный анализ
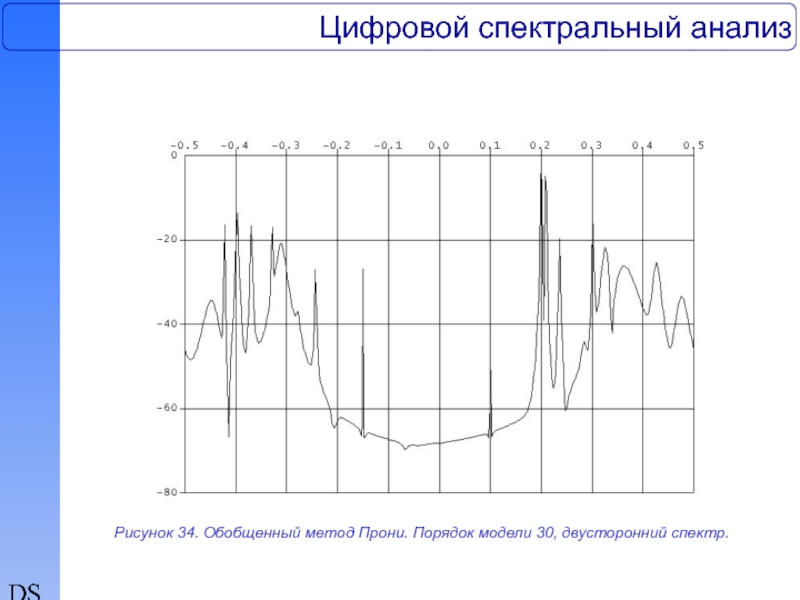
Рисунок 34. Обобщенный метод Прони. Порядок модели 30, двусторонний
Слайд 23DSP
Цифровой спектральный анализ
Рисунок 35. Модифицированный метод Прони. Порядок модели 16, односторонний
Слайд 24DSP
Цифровой спектральный анализ
Рисунок 36. Модифицированный метод Прони. Порядок модели 16, линейчатый
Слайд 25DSP
Цифровой спектральный анализ
Рисунок 37. Модифицированный метод Прони. Порядок модели 30, линейчатый





![DSPЦифровой спектральный анализ Метод наименьших квадратов Прони Предположим, что имеется N комплексных отсчетов данных x[n], .](/img/tmb/2/116319/a884732233042fde884c7f6d45df870b-800x.jpg)


![DSPЦифровой спектральный анализСоотношение (6.73) можно трактовать как моделирующее процесс x[n] с помощью модели авторегрессии и](/img/tmb/2/116319/d4d54fc2a5622e721fa73503a0c948d9-800x.jpg)