- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Множественная регрессия и корреляция презентация
Содержание
- 1. Множественная регрессия и корреляция
- 2. Отбор факторов и выбор формы уравнения
- 4. При отборе факторов в уравнение
- 5. Отбор факторов основан на: теоретическом анализе
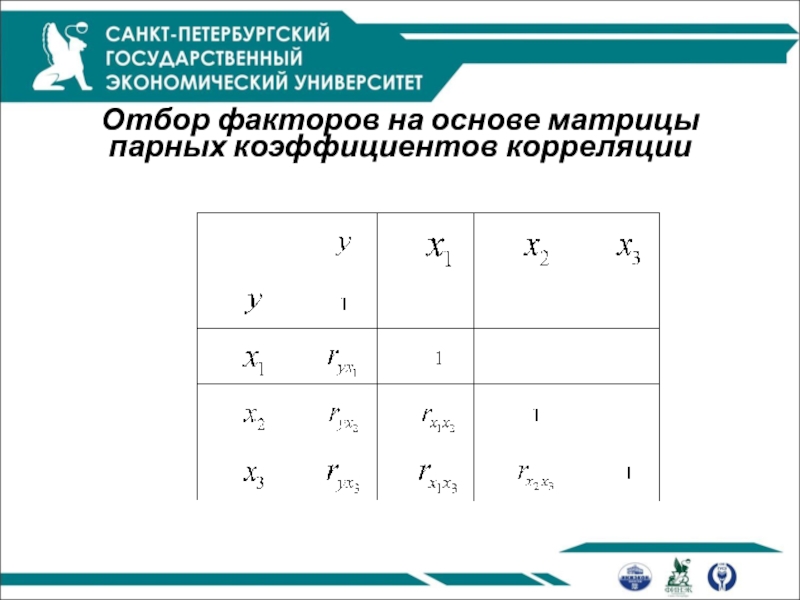
- 6. Отбор факторов на основе матрицы парных коэффициентов корреляции
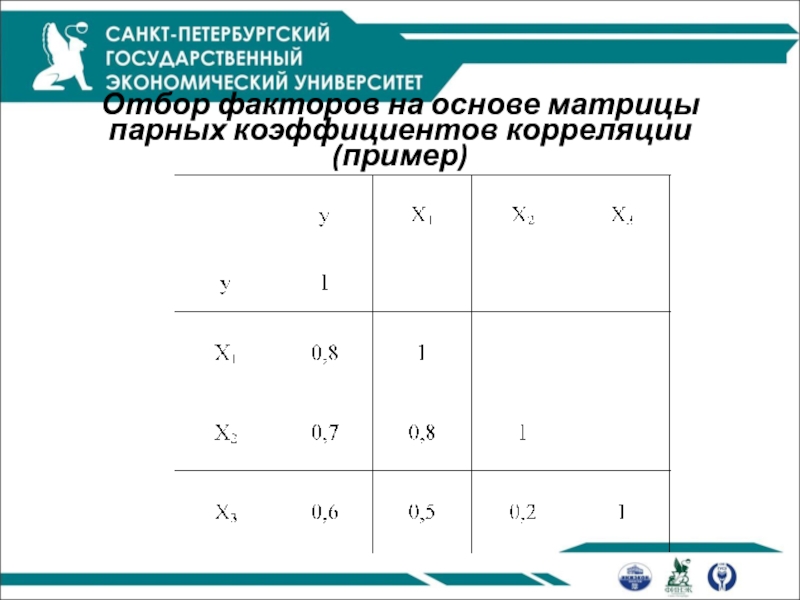
- 7. Отбор факторов на основе матрицы парных коэффициентов корреляции (пример)
- 8. Использование Microsoft Excel для
- 10. Виды функций, наиболее часто используемые в эконометрическом моделировании
- 11. Оценка параметров Для оценки параметров
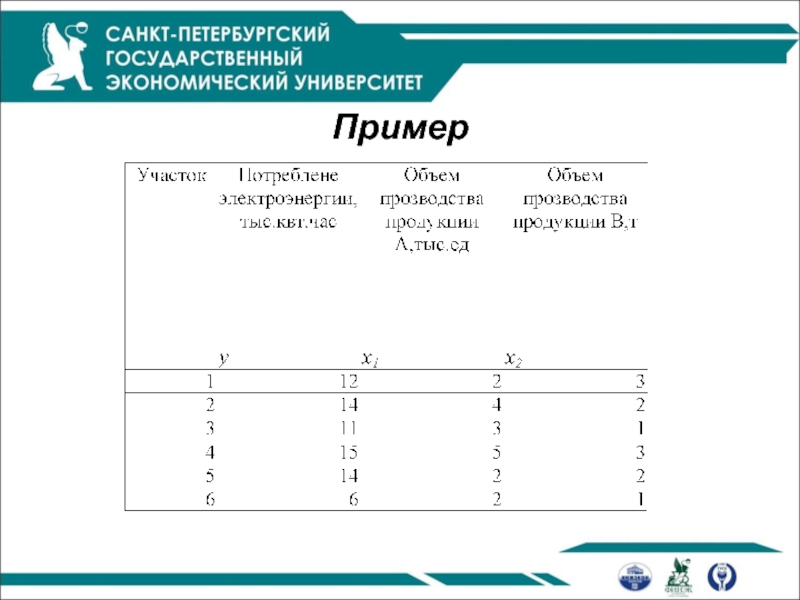
- 12. Пример
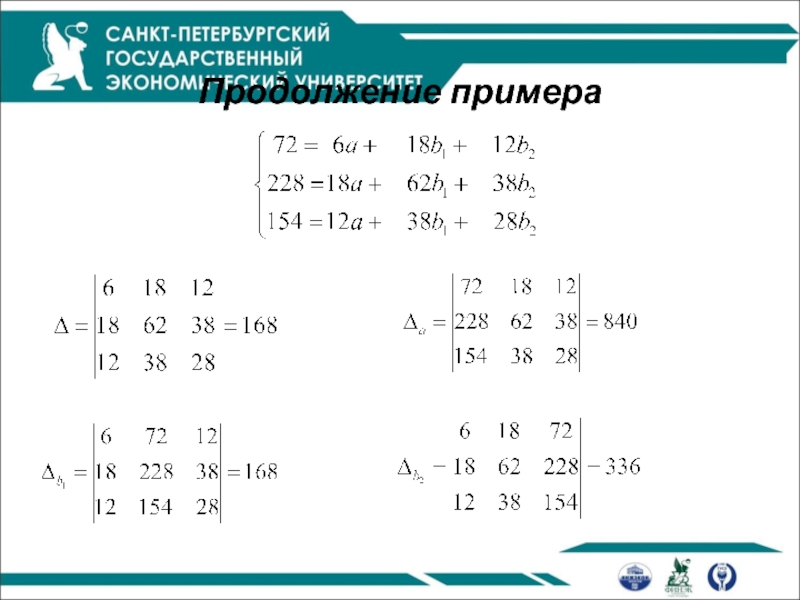
- 13. Продолжение примера
- 14. Продолжение примера
- 15. Продолжение примера
- 17. Пример
- 19. Показатели силы связи в модели
- 20. Абсолютные показатели силы связи
- 21. Относительные показатели связи
- 22. Стандартизованные коэффициенты регрессии (для двухфакторной модели)
- 23. Частные коэффициенты эластичности
- 24. Частные коэффициенты эластичности для
- 25. Коэффициент множественной детерминации
- 26. Продолжение примера
- 27. Продолжение примера
- 28. Продолжение примера. Расчет коэффициента детерминации для линейной функции
- 29. Скорректированный коэффициент детерминации
- 30. Коэффициент (индекс) множественной корреляции
- 31. Коэффициент множественной корреляции
- 32. Показатели частной корреляции
- 33. Показатели частной корреляции
- 34. Показатели частной корреляции
- 35. Оценка достоверности модели
- 36. Таблица дисперсионного анализа
- 37. Оценка достоверности параметров
- 38. Оценка достоверности параметров
- 39. Доверительные интервалы для оцениваемых параметров
- 40. Критерии выбора наилучшей функции
- 41. Использование фиктивных переменных в
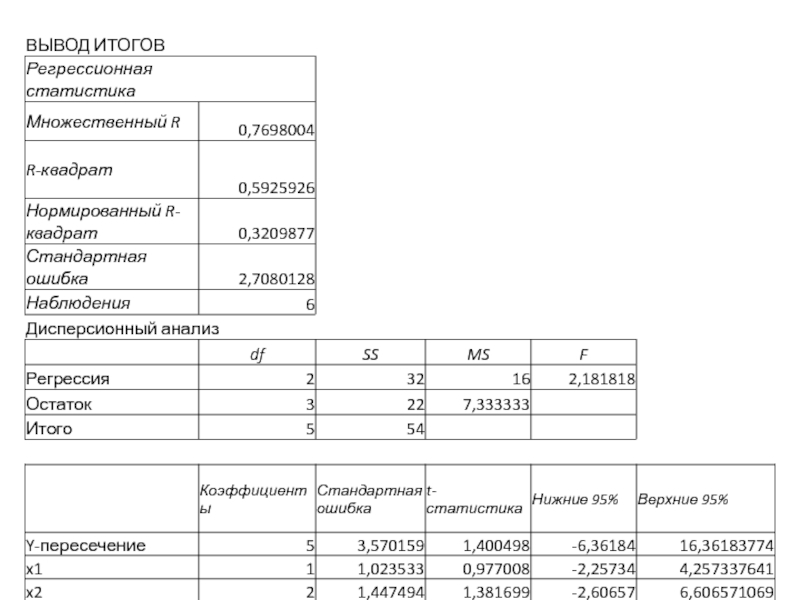
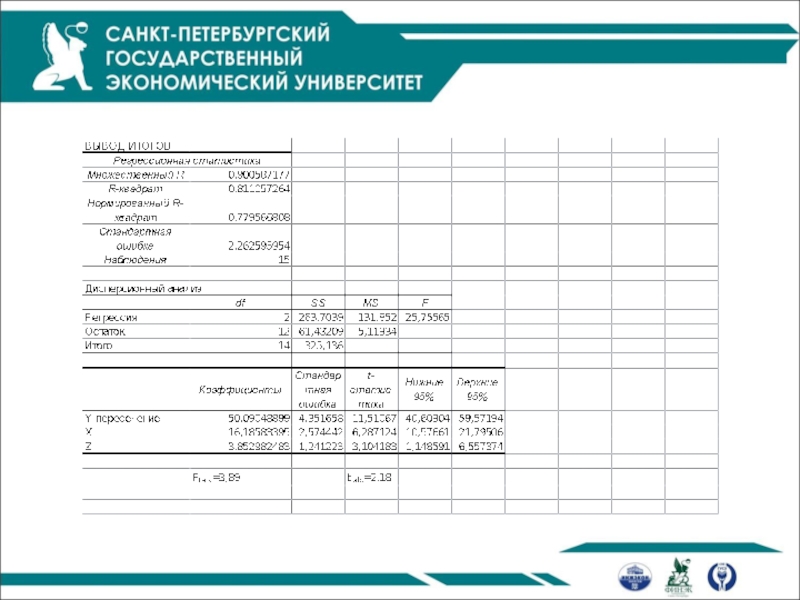
- 42. Пример y – оценочная стоимость
- 43. Пример Z=1- если камин в
- 47. Фиктивные переменные в нелинейных моделях (на примере степенной функции)
- 48. Проблемы, возникающие при построении регрессионных моделей Мультиколлинеарность Гетероскедастичность
- 49. Симптомы мультиколлинеарности Завышенное значение
- 50. Выявление мультиколлинеарности с помощью матрицы
- 51. Меры по устранению мультиколлинеарности
- 52. Гетероскедастичность Основные предпосылки МНК: случайный
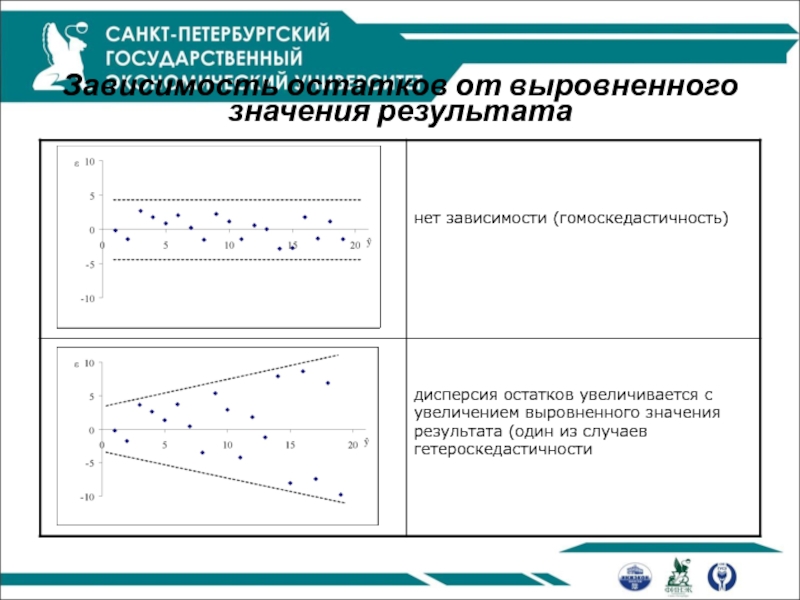
- 53. Зависимость остатков от выровненного значения результата
- 54. Меры по устранению гетероскедастичности Увеличение
- 55. Тесты, используемые для выявления гетероскедастичности Гольдфельда-Квандта Парка Глейзера Уайта
- 56. Тест Гольдфельда-Квандта Все наблюдения упорядочивают
- 57. Тест Гольдфельда-Квандта df1=df2=k-m-1
- 58. Тест Парка
- 59. Тест Глейзера
- 60. Тест Уайта
Отбор факторов и выбор формы уравнения Оценка параметров уравнения множественной регрессии Показатели силы связи в модели множественной регрессии Показатели тесноты связи Оценка достоверности построенного уравнения Использование фиктивных переменных в моделях
Слайд 2
Отбор факторов и выбор формы уравнения
Оценка параметров уравнения множественной регрессии
Показатели силы
связи в модели множественной регрессии
Показатели тесноты связи
Оценка достоверности построенного уравнения
Использование фиктивных переменных в моделях регрессии
Проблемы, возникающие при построении регрессионных моделей: мультиколлинеарность и гетероскедастичность
Показатели тесноты связи
Оценка достоверности построенного уравнения
Использование фиктивных переменных в моделях регрессии
Проблемы, возникающие при построении регрессионных моделей: мультиколлинеарность и гетероскедастичность
Слайд 4
При отборе факторов в уравнение множественной регрессии необходимо соблюдать следующее условия:
в
модель нужно включать только существенные факторы, непосредственно формирующее результат
факторы должны быть количественно измерены
факторы не должны находиться в тесной взаимосвязи друг с другом (значение коэффициента корреляции между факторами, входящими в модель должно быть менее 0,7)
факторы должны быть количественно измерены
факторы не должны находиться в тесной взаимосвязи друг с другом (значение коэффициента корреляции между факторами, входящими в модель должно быть менее 0,7)
Слайд 5
Отбор факторов основан на:
теоретическом анализе взаимосвязи результата с кругом факторов
количественном анализе
(на основе матрицы парных коэффициентов корреляции, матрицы частных коэффициентов корреляции)
Слайд 8
Использование Microsoft Excel для построения матрицы парных коэффициентов корреляции
Анализ данных
Корреляция
В диалоговом
окне «корреляция» задаются следующее параметры
Входной интервал – вводится ссылка на диапазон ячеек, содержащий исходную информацию. Для этого надо выделить исходные данные, записанные в лист Excel. Если данные выделяются с названием граф, то устанавливается флажок метки.
Параметры вывода: выходной интервал (вводится ссылка на любую свободную ячейку на данном рабочем листе); другой рабочий лист или другая рабочая книга.
ОК
Входной интервал – вводится ссылка на диапазон ячеек, содержащий исходную информацию. Для этого надо выделить исходные данные, записанные в лист Excel. Если данные выделяются с названием граф, то устанавливается флажок метки.
Параметры вывода: выходной интервал (вводится ссылка на любую свободную ячейку на данном рабочем листе); другой рабочий лист или другая рабочая книга.
ОК
Слайд 11
Оценка параметров
Для оценки параметров уравнения множественной регрессии применяют метод наименьших квадратов
(МНК). При этом нелинейные функции приводятся к линейному виду по параметрам.
Слайд 19
Показатели силы связи в модели множественной регрессии
Абсолютные
Относительные
Стандартизованные коэффициенты регрессии
Частные коэффициенты эластичности
Слайд 20
Абсолютные показатели силы связи
Показывают, на сколько единиц в среднем изменяется результативный
признак при изменении рассматриваемого факторного признака на одну единицу при условии, что остальные факторы зафиксированы на среднем уровне и не меняются
Слайд 32
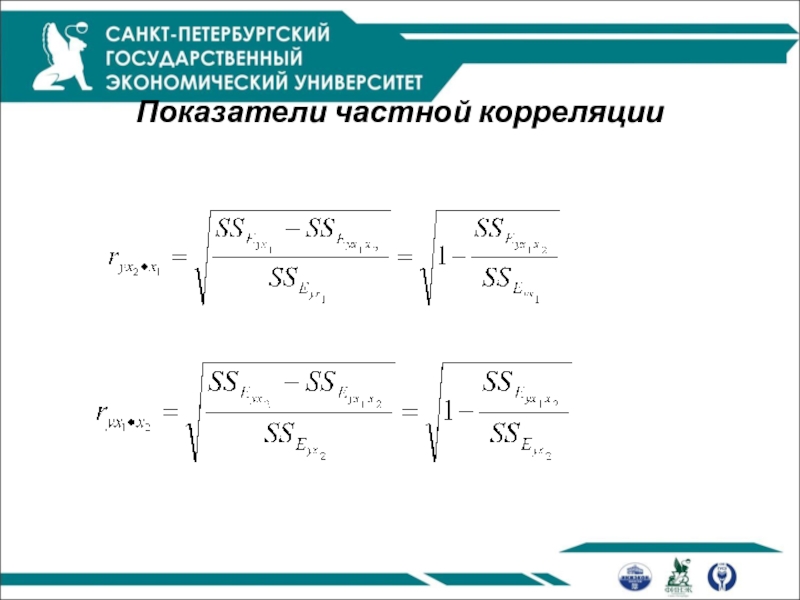
Показатели частной корреляции
основаны на соотношении сокращения остаточной вариации за счет
дополнительно включенного в модель фактора к остаточной вариации до включения в модель соответствующего фактора
Слайд 39
Доверительные интервалы для оцениваемых параметров
Доверительный интервал позволяет:
Оценить значимость параметра (параметр будет
значим, если в доверительный интервал не входит ноль).
Дать экономическую интерпретацию коэффициента регрессии (с вероятностью (1‑α) при единичном изменении независимой переменной xj зависимая переменная у изменится не меньше, чем на bj,min и не больше, чем на bj,max .
Дать экономическую интерпретацию коэффициента регрессии (с вероятностью (1‑α) при единичном изменении независимой переменной xj зависимая переменная у изменится не меньше, чем на bj,min и не больше, чем на bj,max .
Слайд 40
Критерии выбора наилучшей функции
Минимальная доля остаточной дисперсии в общей дисперсии,
то есть максимальная величина коэффициента детерминации R2. Если модели регрессии содержат разное количество параметров, вместо R2 следует сравнивать скорректированные коэффициенты детерминации R2скорр.
Статистическая значимость всех параметров при независимых переменных
Значимость всей функции в целом
Выполнение требований Гаусса-Маркова, предъявляемых к случайным остаткам модели, в первую очередь, постоянство дисперсии и независимость друг от друга
Статистическая значимость всех параметров при независимых переменных
Значимость всей функции в целом
Выполнение требований Гаусса-Маркова, предъявляемых к случайным остаткам модели, в первую очередь, постоянство дисперсии и независимость друг от друга
Слайд 41
Использование фиктивных переменных в моделях регрессии
Фиктивная (структурная) переменная – это переменная,
принимающая значение 1 или 0.
Используется при решении следующих задач:
при моделировании качественных признаков
для учета структурной неоднородности, к которой приводят качественные признаки
для оценки сезонных колебаний
Используется при решении следующих задач:
при моделировании качественных признаков
для учета структурной неоднородности, к которой приводят качественные признаки
для оценки сезонных колебаний
Слайд 42
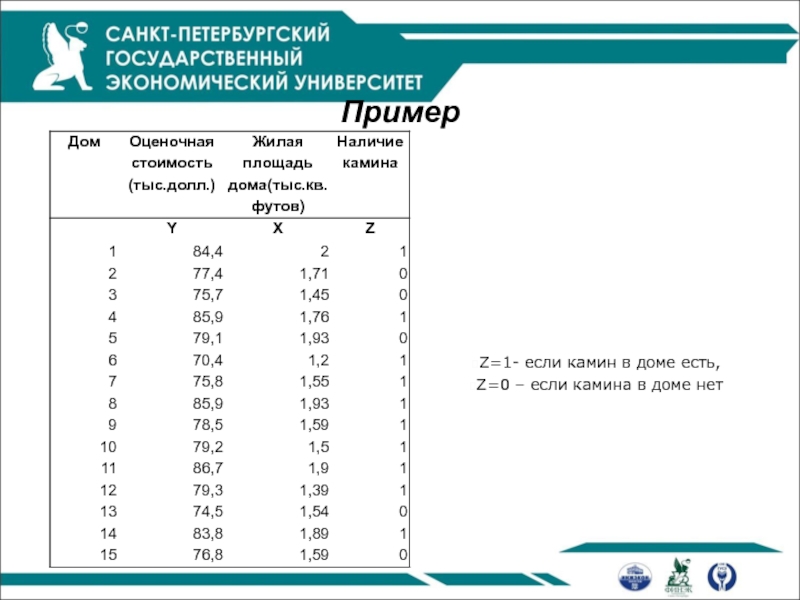
Пример
y – оценочная стоимость жилья
x – жилая площадь
z – наличие камина
(1- есть камин, 0 – нет камина)
Слайд 48
Проблемы, возникающие при построении регрессионных моделей
Мультиколлинеарность
Гетероскедастичность
Слайд 49
Симптомы мультиколлинеарности
Завышенное значение коэффициента детерминации
Высокие стандартные ошибки для коэффициентов регрессии
Широкие доверительные
интервалы
Низкое значение t-критерия
Появление при коэффициентах регрессии знаков, противоположных ожидаемым
Низкое значение t-критерия
Появление при коэффициентах регрессии знаков, противоположных ожидаемым
Слайд 50
Выявление мультиколлинеарности с помощью матрицы парных коэффициентов корреляции
Наличие мультиколлинеарности можно
подтвердить, найдя определитель матрицы. Если связь между независимыми переменными полностью отсутствует, то недиагональные элементы будут равны нулю, а определитель матрицы ‑ единице.
Если связь между независимыми переменными близка к функциональной (то есть является очень тесной), то определитель матрицы будет близок к нулю.
Если связь между независимыми переменными близка к функциональной (то есть является очень тесной), то определитель матрицы будет близок к нулю.
Слайд 51
Меры по устранению мультиколлинеарности
Удаление из модели переменных с высоким коэффициентом парной
корреляции между факторами, если это не противоречит теории, положенной в основу построения модели
Увеличение числа наблюдений
Изменение функциональной формы модели
Функциональные преобразования тесно связанных между собой переменных. Например, поступление налогов в городах зависит от количества жителей и площади города. Очевидно, что эти переменные будут тесно связаны. Их можно заменить одной относительной переменной «плотность населения»
Построение моделей по отклонениям от средней величины
Использование специальных методов обработки временных рядов
Увеличение числа наблюдений
Изменение функциональной формы модели
Функциональные преобразования тесно связанных между собой переменных. Например, поступление налогов в городах зависит от количества жителей и площади города. Очевидно, что эти переменные будут тесно связаны. Их можно заменить одной относительной переменной «плотность населения»
Построение моделей по отклонениям от средней величины
Использование специальных методов обработки временных рядов
Слайд 52
Гетероскедастичность
Основные предпосылки МНК:
случайный характер остатков
нулевая средняя остатков, не зависящая от фактора
x
гомоскедастичность (дисперсия каждого отклонения одинакова для всех значений x)
отсутствие автокорреляции остатков
остатки должны подчиняться нормальному распределению
гомоскедастичность (дисперсия каждого отклонения одинакова для всех значений x)
отсутствие автокорреляции остатков
остатки должны подчиняться нормальному распределению
Слайд 54
Меры по устранению гетероскедастичности
Увеличение числа наблюдений
Изменение функциональной формы модели
Разделение исходной совокупности
на качественно-однородные группы и проведение анализа в каждой группе
Использование фиктивных переменных, учитывающих неоднородность
Исключение из совокупности единиц, дающих неоднородность
Использование фиктивных переменных, учитывающих неоднородность
Исключение из совокупности единиц, дающих неоднородность
Слайд 55
Тесты, используемые для выявления гетероскедастичности
Гольдфельда-Квандта
Парка
Глейзера
Уайта
Слайд 56
Тест Гольдфельда-Квандта
Все наблюдения упорядочивают по мере возрастания какого-либо фактора, который, как
предполагается, оказывает влияние на возрастание дисперсии остатков
Упорядоченную совокупность делят на три группы, причем первая и последняя должны быть равного объема с числом единиц, больших, чем число параметров модели регрессии. Число отобранных единиц обозначим k
По первой и третьей группе находят параметры уравнений регрессии и остатки по ним
Используя данные об остатках моделей первой и третьей группы, рассчитывают фактическое значение F-критерия
Упорядоченную совокупность делят на три группы, причем первая и последняя должны быть равного объема с числом единиц, больших, чем число параметров модели регрессии. Число отобранных единиц обозначим k
По первой и третьей группе находят параметры уравнений регрессии и остатки по ним
Используя данные об остатках моделей первой и третьей группы, рассчитывают фактическое значение F-критерия
