Методы статистического анализа презентация

медицинских исследованиях, которая в лучшем случае характеризуется параметрическими показателями, критерием Стьюдента и коэффициентом линейной парной корреляции Браве-Пирсона

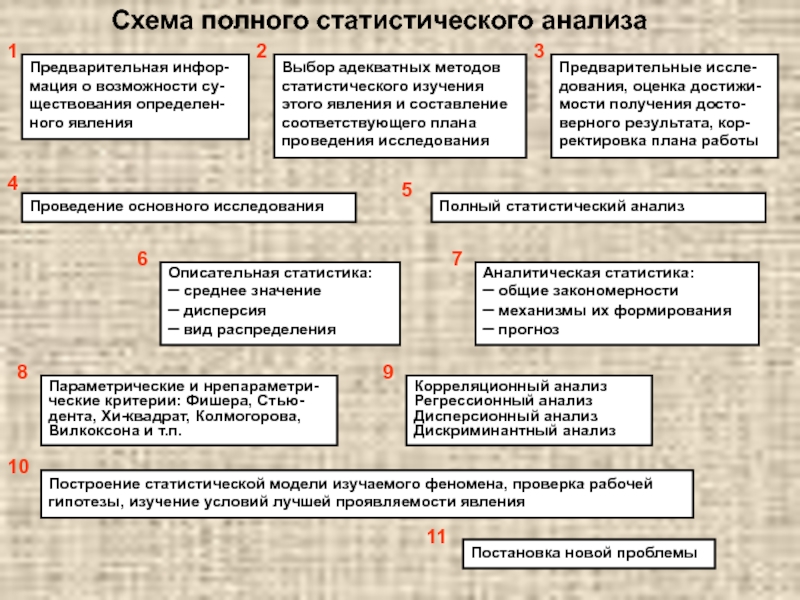
Практически отсутствует системный подход к статистическому анализу: применение той или иной его разновидности ничем специально не обосновывается и не диктуется логикой научного исследования

Игнорируется предшествующее любой научной работе статистическое планирование, которое само может и должно определять структуру исследовательской работы и оптимальный методический минимум

Низкая культура преподавания высшей математики и информатики особенно в медицинских вузах, которая постепенно трансформируется в научные исследования с неэффективными практическими рекомендациями

биометрии - науки, вспомогательной в медико-биологических исследованиях, но придающей им законченный описательный и достоверный смысл

Основные задачи биометрии - описание явления, оценка его достоверности (воспроизводимости), изучение механизмов его развития (во взаимосвязи с другими процессами и явлениями) и условий его максимального проявления, принятие решения (прогноз, предсказание, экстраполяция)

Ученый, который открыл некоторые новые явления, зависимости, тенденции, на этом построил рабочую гипотезу должен защитить ее от предположения, что все эти явления и эффекты не обусловлены случаем. Он должен оценить, сколько необходимо провести наблюдений, чтобы доказать наличие достоверного результата

плана работы

Выбор адекватных методов статистического изучения этого явления и составление соответствующего плана проведения исследования

Предварительная инфор-мация о возможности су-ществования определен-ного явления

Проведение основного исследования

Полный статистический анализ

Описательная статистика: – среднее значение – дисперсия – вид распределения

Аналитическая статистика: – общие закономерности – механизмы их формирования – прогноз

Параметрические и нрепараметри-ческие критерии: Фишера, Стью-дента, Хи-квадрат, Колмогорова, Вилкоксона и т.п.

Корреляционный анализ Регрессионный анализ Дисперсионный анализ Дискриминантный анализ

Построение статистической модели изучаемого феномена, проверка рабочей гипотезы, изучение условий лучшей проявляемости явления

Постановка новой проблемы

1

2

3

4

5

6

7

8

9

10

11

Х +1 σ +2 σ +3 σ

68,3%

95,5%

99,9%

Х = (х1+ х2 + … +хn) / n
σ = √(∑x2i - (∑xi)2/n) / (n-1)
m = σ / √n

Основные параметры нормального распределения

0,412±0,0217
7,0±0,063 7,03±0,063
12,33±0,15 12,3±0,15
384,54±18,608 385±18,6

Правило 1
Точность представления среднего значения зависит от его величины
До 1 – три знака после запятой
От 1 до 10 – два знака после запятой
От 10 до 100 – один знак после запятой
Свыше 100 – целое число.

Правило 2
Ошибка среднего значения пишется на один знак точнее среднего значения

r ) от -1 до +1

Частная корреляция

Нелинейная зависимость:
корреляционное отношение ( η2 ) от 0 до +1

Непараметрическая корреляция

Ранговая корреляция Спирмена ( ρ ) от -1 до +1

Абсолютные значения коэффициента корреляции слабая зависимость < 0,3 средняя зависимость 0,3 - 0,6 сильная зависимость 0,3 - 0,9

Корреляционные плеяды

Бисериальная корреляция

***
********
**************
************************
********************************
******************************
********************
**********
***

***
********
**************
************************
********************************
******************************
********************
**********
***

***
***** *****
*********** *************
********* **************
******** ***********
********* *********
******** *********

х

х

y

y

y

х

r = +0,64

r = -0,58

r = 0,0

η2 = 0,84

влияния одного параметра на другой

Парная регрессия
Y = aX + b

Множественная регрессия
Y = a1X1 + a2X2 + … anXn + b

Регрессионный анализ позволяет строить прогностические модели - по изменению одного (или нескольких) показателей предсказывать изменение какого-либо параметра

является результатом действия факторов, часть из которых врач контролирует, а часть – нет (т.е. влияние могут оказать случайные факторы)

Дисперсионный анализ применяют в многофакторных моделях; он позволяет выделить ту часть динамических процессов, которая определяется тем или иным контролируемым фактором. Главное условие применения этого вида анализа – необходимость выделения градаций внутри каждого фактора

влияний скрытые факторы, которые по тем или иным причинам врач не контролирует.
Типичный вывод после проведения факторного анализа: изменение параметра Х в процессе лечения на 12% объясняется выбранной методикой лечения, 39% изменений – результат случайных воздействий, но другие 49% объясняются влиянием, например, трех неучтенных факторов (F1 – 25%; F2 – 11%’ F3 – 13%)

системы

Построение уравнения разграничительной функции для разделения пациентов на различные классы (диагностика)

Выделение из суммы параметров важнейших, которые вносят значимый вклад в уравнение разграничительной функции

Вилкоксона

Непараметрическая корреляция
Ранговая корреляция Спирмена
Корреляция Кендала
Критерий ассоциации Пирсона

Оценка формы распределения встречаемости признака
Критерий Пирсона χ2