класса «Б»: Жевагина Анна, Исаков Вадим, Чекмезова Виктория, Абанькин Артем, Харавин Арсений
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы решения тригонометрических уравнений презентация
Содержание
- 1. Методы решения тригонометрических уравнений
- 2. Существует несколько методов решения тригонометрических уравнений: Введение
- 3. Введение новой переменной
- 4. Разложение на множители Пример : 2sinxcosx
- 5. Однородное уравнение I степени Пример : 2sinx –3cosx=0
- 6. Однородное уравнение II степени Пример :
- 7. Метод вспомогательного аргумента Пример : √3 sin2x-cos2x=1
- 8. Метод универсальной подстановки
- 9. Спасибо за внимание!
Существует несколько методов решения тригонометрических уравнений: Введение новой переменной Разложение на множители Однородное уравнение I степени Однородное уравнение II степени Метод вспомогательного аргумента Метод универсальной подстановки
Слайд 1Методы решения тригонометрических уравнений
В создании проекта по алгебре
принимали участие ученики 10
Слайд 2Существует несколько методов решения тригонометрических уравнений:
Введение новой переменной
Разложение на множители
Однородное уравнение I степени
Однородное уравнение II степени
Метод вспомогательного аргумента
Метод универсальной подстановки
Однородное уравнение II степени
Метод вспомогательного аргумента
Метод универсальной подстановки
Слайд 3
Введение новой переменной
Пример :
2 sin2 x + sin x – 1 =
0
Пусть sin x = y
2y2 + y – 1 = 0
D = b2 – 4ac = 1 – 4 ∙ 2 ∙ (–1) = 1 + 8 = 9
√D = 3
y1= (-1+3)/4 = ½
y2= (-1-3)/4 = -1
sin x = ½ sin x = -1
Х = П/6+Пn x = 3Пn/2+Пn
n ͼ z
Пусть sin x = y
2y2 + y – 1 = 0
D = b2 – 4ac = 1 – 4 ∙ 2 ∙ (–1) = 1 + 8 = 9
√D = 3
y1= (-1+3)/4 = ½
y2= (-1-3)/4 = -1
sin x = ½ sin x = -1
Х = П/6+Пn x = 3Пn/2+Пn
n ͼ z
Формулы:
sin x = y
D = b2 – 4ac
y1,2 =(–b ± √D)/2a
Слайд 4Разложение на множители
Пример :
2sinxcosx – sinx = 0
sinx(2cosx-1) = 0
sinx=0
2cosx-1=0
x= Пn+Пn 2cosx=1
2x=1
x= ½
x=П/3+Пn
n ͼ z
x= Пn+Пn 2cosx=1
2x=1
x= ½
x=П/3+Пn
n ͼ z
Формулы:
sinxcosx±sinx=0
sin(cosx±1)=0
cosxsinx±cosx=0
cosx(sinx±1)=0
Слайд 5Однородное уравнение I степени
Пример :
2sinx –3cosx=0 |cosx≠0
2 tg x – 3 = 0
2 tg x =
3
tg x=3/2
x = arctg3/2+Пn
n ͼ z
tg x=3/2
x = arctg3/2+Пn
n ͼ z
Формулы:
Asinx+Bsinx=0 |cosx≠0
Asinx+Bsinx=0 |sins ≠0
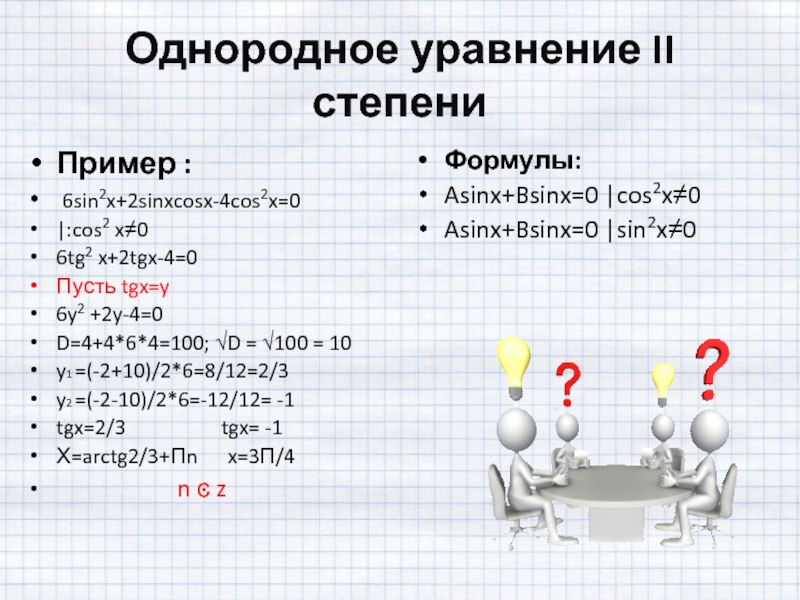
Слайд 6Однородное уравнение II степени
Пример :
6sin2x+2sinxcosx-4cos2x=0
|:cos2 x≠0
6tg2 x+2tgx-4=0
Пусть tgx=y
6y2 +2y-4=0
D=4+4*6*4=100;
√D = √100 = 10
y1 =(-2+10)/2*6=8/12=2/3
y2 =(-2-10)/2*6=-12/12= -1
tgx=2/3 tgx= -1
Х=arctg2/3+Пn x=3П/4
n ͼ z
y1 =(-2+10)/2*6=8/12=2/3
y2 =(-2-10)/2*6=-12/12= -1
tgx=2/3 tgx= -1
Х=arctg2/3+Пn x=3П/4
n ͼ z
Формулы:
Asinx+Bsinx=0 |cos2x≠0
Asinx+Bsinx=0 |sin2x≠0
Слайд 7Метод вспомогательного аргумента
Пример :
√3 sin2x-cos2x=1 |:2
C= √ (√3 )2+ (1)2 =2
√3/2sin2x
-1/2cos2x= ½
cosП/6sin2x-sin П/6cos2x= ½
Sin(2x- П/6)= ½
2x- П/6=П/6+2Пn 2x-П/6=П-П/6+2Пn
2x=П/3+2Пn │:2 2x=П+2Пn │:2
x=П/6+Пn x= П/2+Пn
n ͼ z
cosП/6sin2x-sin П/6cos2x= ½
Sin(2x- П/6)= ½
2x- П/6=П/6+2Пn 2x-П/6=П-П/6+2Пn
2x=П/3+2Пn │:2 2x=П+2Пn │:2
x=П/6+Пn x= П/2+Пn
n ͼ z
Формулы:
Asinx+Bsinx=Csin(x+t)
C= √A2+B 2
sint=B/C
│→ t
cost=A/C
Слайд 8
Метод универсальной подстановки
Пример :
3sinx-4cosx=5
Пусть tg x/2=t, тогда sinx=2t/1+t2
cosx=(1-t 2)/(1+t2)
x≠П+2Пn
-6t+4-4t 2+5+5t2=0
t 2-6t+9=0
(t-3) 2 =0; t=3
tg x/2=3
x/2=arctg3+Пn
X=2arctg3+2Пn
n ͼ z
-6t+4-4t 2+5+5t2=0
t 2-6t+9=0
(t-3) 2 =0; t=3
tg x/2=3
x/2=arctg3+Пn
X=2arctg3+2Пn
n ͼ z
Формулы:
cosx=(1-tg 2 x/2)/
/(1+tg2 x/2)
Sinx=(2tgx/2)/
/(1+tg 2 x/2)
x≠П+2Пn
