- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы построения математических моделей на основе активного эксперимента презентация
Содержание
- 1. Методы построения математических моделей на основе активного эксперимента
- 2. Оптимальное планирование эксперимента при изучении свойств многокомпонентных
- 3. 1. Особенности планирования эксперимента при изучении свойств
- 5. 2 . Вид уравнений для описания свойств
- 7. 3. Симплекс – решетчатые планы (СРП) Шеффе
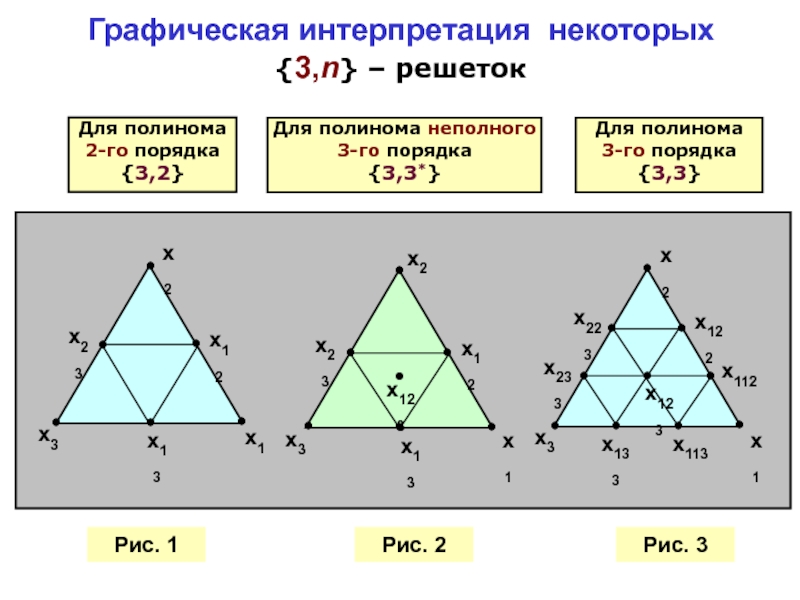
- 8. Графическая интерпретация некоторых {3,n} – решеток
- 9. Симплекс-решетчатые планы являются частично композиционными:
- 10. Примеры построения матриц планирования для решеток {3,2}
- 11. 2) Матрица планирования для {3,3}-решетки. (см. рис. 3)
- 12. 4. Вычисление коэффициентов приведенных полиномов Шеффе
- 15. 5. Проверка адекватности УР
- 16. При этом, если l
- 18. ПОСТРОЕНИЕ СИМПЛЕКС-РЕШЁТЧАТЫХ ПЛАНОВ И ПОЛИНОМОВ ШЕФФЕ Лабораторная
- 19. 1. Физический смысл задачи
- 20. 2. Математический смысл и геометрическая интерпретация задачи
- 22. 6. Планирование эксперимента при исследовании МКС на локальных участках диаграмм
- 24. Значения
- 26. ОЦЕНКА АДЕКВАТНОСТИ ПОЛИНОМОВ ШЕФФЕ
Слайд 2Оптимальное планирование эксперимента при изучении свойств многокомпонентных систем (МКС)
1. Особенности планирования
2. Вид уравнений для описания свойств МКС. Приведенные полиномы Шеффе.
3. Симплекс – решетчатые планы Шеффе.
4. Вычисление коэффициентов приведенных полиномов Шеффе.
5. Проверка адекватности уравнения регрессии.
6. Планирование эксперимента при исследовании МКС на локальных участках диаграмм.
Слайд 31. Особенности планирования эксперимента при изучении свойств смесей
При изучении
где xi ≥0 – концентрация i-го компонента в смеси;
q – количество компонентов в смеси;
представляет собой правильный (q–1)-мерный симплекс.
Симплекс в k – мерном пространстве это выпуклый многогранник, имеющий ровно (k+1) вершину, каждая из которых определяется пересечением k гиперплоскостей данного пространства:
для двухкомпонентных систем симплекс – прямая линия;
для трехкомпонентных систем правильный симплекс –
равносторонний треугольник;
для четырехкомпонентных систем симплекс – тетраэдр.
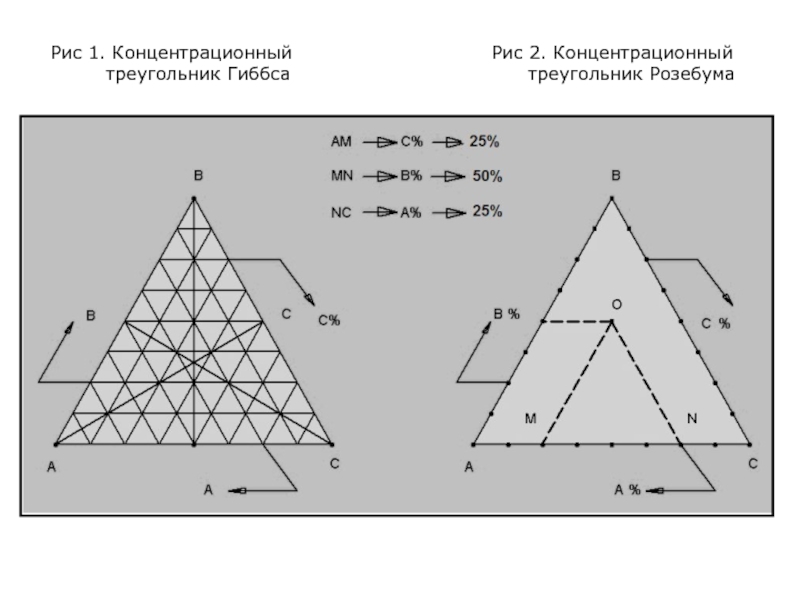
На рис. 1 и 2 представлены разновидности представления трехкомпонентных систем на двухмерном симплексе.
(1)
Слайд 52 . Вид уравнений для описания свойств МКС. Приведенные полиномы Шеффе
Поверхности отклика в МКС имеют сложный характер, поэтому для адекватного описания таких поверхностей требуются полиномы высоких степеней и, как следствие, большое количество опытов.
Обычный полином степени n от q переменных имеет
коэффициентов
где – концентрации компонентов смеси.
Шеффе ввел каноническую форму полинома (приведенные полиномы),
число коэффициентов которого значительно меньше, чем обычного.
Рассмотрим, в качестве примера, получение приведенного полинома
второй степени для тройной системы.
Обычный полином (содержит 10 коэффициентов):
Слайд 73. Симплекс – решетчатые планы (СРП) Шеффе
Симплекс – решетчатые планы являются насыщенными планами, то есть число опытов в этих планах равно числу неизвестных коэффициентов полинома.
Алгоритм построения плана заключается в следующем:
а) определяется шаг изменения концентрации компонентов 1/n,
где n – степень полинома;
б) по каждому компоненту задается (n+1) одинаково расположенных
уровней:
в) выбираются все возможные комбинации с такими значениями
концентраций компонентов, которые удовлетворяют
нормирующему соотношению (1).
Слайд 9Симплекс-решетчатые планы являются
частично композиционными:
неполную кубическую решетку {3,3*}
можно получить
(см. рис 2.);
решетку {3,4} получают добавлением соответствующих точек к решетке {3,2}.
Слайд 10Примеры построения матриц планирования для решеток {3,2} и {3,3}
1) Матрица
(см. рис. 1)
Слайд 16 При этом, если l >2, то адекватность можно
при условии однородности усредняемых дисперсий, полученных по параллельным опытам во всех точках симплекса, проверяемой по критерию Кохрена.
Остаточная дисперсия (дисперсия адекватности ) в этом случае определяется по контрольным точкам (КТ)
где; l – число контрольных точек; fост= l – 1 – число степеней свободы остаточной дисперсии; – средние экспериментальные значения выходной переменной в КТ; – значения, рассчитанные в соответствующих КТ по УР.
(6)
Слайд 18ПОСТРОЕНИЕ СИМПЛЕКС-РЕШЁТЧАТЫХ ПЛАНОВ И ПОЛИНОМОВ ШЕФФЕ
Лабораторная работа №4
“Оптимальное планирование эксперимента при
Слайд 19 1. Физический смысл задачи
При создании композиционных,
Довольно часто в качестве ТДН используют зерненые наполнители, которые характеризуются средне-массовым размером частиц и пористостью. Под порис-тостью понимается величина объема не занятого частицами наполнителя после заполнения ими единичного объема, например равного 1дм3.
В некоторых случаях, с целью улучшения физико-механических и других свойств материала, возникает необходимость увеличения доли единичного объема занятого наполнителями. Для этого в состав материала вводят в соответствующих объемных долях фракции наполнителя с разными средне-массовыми размерами частиц и пористостями. В результате плотность упаковки смеси ТДН (доля объема занятого в единичном объеме фракциями наполнителя – параметр φm ) возрастает. Плотность упаковки φm зависит от размеров частиц di , пористостей pi выбранных фракций, их долей vi в составе наполнителя и может быть рассчитана через указанные параметры известными методами.
В лабораторной работе необходимо для заданных числа фракций ТДН и степени полинома Шеффе: построить симплекс-решетчатый план относительно объемных долей фракций; рассчитать в точках плана по соответствующей программе значения φm; по результатам вычислительного эксперимента определить коэффициенты полинома и оценить его адекватность путем расчета по нему φm в контрольных точках (КТ). В формализованном виде смысл и геометрическая интерпретация задачи представлены на следующем слайде.