- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Преобразование алгебраических выражений презентация
Содержание
- 1. Преобразование алгебраических выражений
- 2. Структура урока: 1.Сообщение темы,целей и задач
- 3. Цели и задачи: Цели урока: Систематизировать и
- 4. А́лгебра (от араб. الجبر, «аль-джабр» — восполнение) — раздел математики) — раздел математики, который можно грубо
- 5. Вынесение общего множителя за скобки: Разложение многочленов на множители
- 6. Способ группировки Разложение многочленов на множители
- 7. Разложение на множители квадратного трехчлена Разложение многочленов на множители
- 8. Применение формул сокращенного умножения Разложение многочленов на множители
- 9. ФОРМУЛЫ СОКРАЩЁННОГО УМНОЖЕНИЯ (a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2 (a+b)(a-b)=a2-b2 (a+b)(a2-ab+b2)=a3+b3 (a-b)(a2+ab+b2)=a3-b3 (a+b)3=a3+3a2b+3ab2+b3 (a-b)3=a3-3a2b+3ab2-b3
- 10. №1. Преобразуйте в многочлен:
- 11. №2. Разложите на множители: 1) 81
- 12. В 988 году, во времена правления киевского
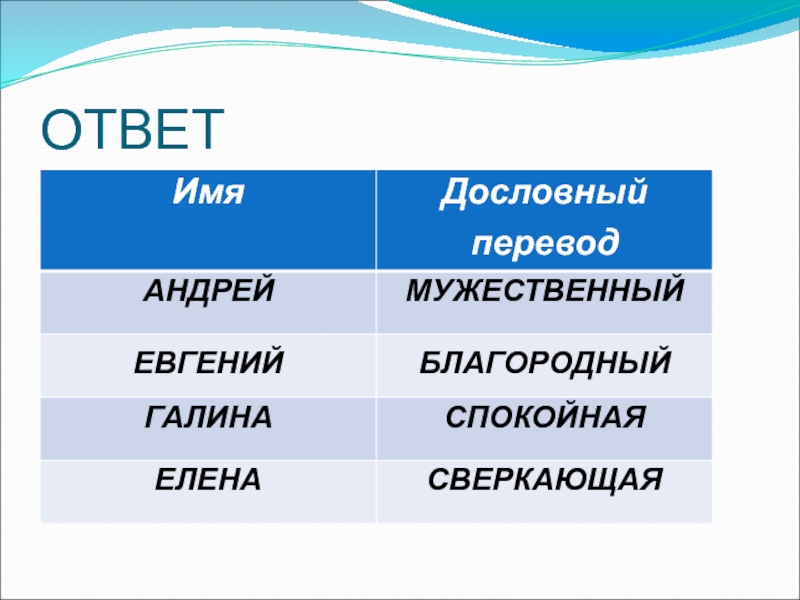
- 14. ОТВЕТ
- 15. Домашнее задание № 3.26 (1,2.), № 3.27.
- 16. Спасибо за урок!
Структура урока:
1.Сообщение темы,целей и задач урока. 2. Повторение теоретического материала и его применение на простых примерах с помощью устного счета.
3. Решение заданий на преобразование алгебраических выражений. Самостоятельная работа-шифровка.
Слайд 1
Преобразование
алгебраических выражений
Николенко Денис Владимирович,
преподаватель ОБОУ СПО «Курский техникум связи»
Слайд 2Структура урока:
1.Сообщение темы,целей и задач урока.
2. Повторение теоретического материала и его
применение на простых примерах с помощью устного счета.
3. Решение заданий на преобразование алгебраических выражений. Самостоятельная работа-шифровка.
4. Контроль и самоконтроль знаний. Проверочная самостоятельная работа с использованием тестов.
5. Задание на дом.
6. Подведение итогов урока. 8. Рефлексия. «Барометр настроения».
6. Подведение итогов урока. 8. Рефлексия. «Барометр настроения».
Слайд 3Цели и задачи:
Цели урока: Систематизировать и обобщить теоретические знания по теме
«Преобразования алгебраических выражений».
Совершенствовать навыки решения заданий на преобразование алгебраических выражений.
Задачи: 1. Развитие навыков в применения всех способов преобразования алгебраических выраженийс целью подготовки к успешной сдаче зачета по математике (модуль «Алгебра»); 2. Формировать потребность к самопознанию; умение ставить цели и реализовывать их.
Совершенствовать навыки решения заданий на преобразование алгебраических выражений.
Задачи: 1. Развитие навыков в применения всех способов преобразования алгебраических выраженийс целью подготовки к успешной сдаче зачета по математике (модуль «Алгебра»); 2. Формировать потребность к самопознанию; умение ставить цели и реализовывать их.
Слайд 4А́лгебра (от араб. الجبر, «аль-джабр» — восполнение) — раздел математики) — раздел математики, который можно грубо охарактеризовать как обобщение и
расширение арифметики) — раздел математики, который можно грубо охарактеризовать как обобщение и расширение арифметики. Слово «алгебра» также употребляется в названиях различных алгебраических систем) — раздел математики, который можно грубо охарактеризовать как обобщение и расширение арифметики. Слово «алгебра» также употребляется в названиях различных алгебраических систем. В более широком смысле под алгеброй понимают раздел математики, посвящённый изучению операций над элементами множества произвольной природы, обобщающий обычные операции сложения и умножения чисел.
Трёхмерный правильный коноид, описанный алгебраическими тригонометрическими уравнениями.
Слайд 9ФОРМУЛЫ СОКРАЩЁННОГО УМНОЖЕНИЯ
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
(a+b)(a-b)=a2-b2
(a+b)(a2-ab+b2)=a3+b3
(a-b)(a2+ab+b2)=a3-b3
(a+b)3=a3+3a2b+3ab2+b3
(a-b)3=a3-3a2b+3ab2-b3
Слайд 11№2. Разложите на множители:
1) 81 в2 – 0,09n2 =
2)
3ха2 +30хас+ 75с2х =
3) у2 - 13 =
4) 5 – а =
5) х3 + 27d 3 =
6) 4n10 – 0, 01а6 =
3) у2 - 13 =
4) 5 – а =
5) х3 + 27d 3 =
6) 4n10 – 0, 01а6 =
Слайд 12В 988 году, во времена правления киевского князя Владимира, Русь приняла
христианство. Вместе с религией на Русь попали и древнегреческие имена. Выполните действия с алгебраическими выражениями и по совпадающим ответам соотнесите греческие имена с их дословными переводами.
