- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы оптимизации презентация
Содержание
- 1. Методы оптимизации
- 2. Под оптимизацией понимают процесс выбора наилучшего варианта
- 3. Выбор оптимального решения или сравнение двух альтернативных
- 4. Задачи оптимизации. Безусловная задача оптимизации состоит в
- 5. В результате ограничений область проектирова-ния а, определяемая всеми п проектными
- 6. В ряде случаев из этих соотношений можно
- 7. Одномерная оптимизация.
- 8. Теорема Вейерштрасса. Всякая функция f(x),
- 9. Многомерная оптимизация. Метод нулевого порядка не
- 10. Методы безусловной оптимизации. Хука и Дживса
- 11. Метод Нелдера - Мида, также известный как метод деформируемого
- 14. Эволюционные алгоритмы Эволюционные алгоритмы - направление в
- 15. Цель исследования Выяснить, для каких функций люди
Слайд 2Под оптимизацией понимают процесс выбора наилучшего варианта из всех возможных
В
Основные понятия.
Слайд 3Выбор оптимального решения или сравнение двух альтернативных решений проводится с помощью
В процессе решения задачи оптимизации должны быть найдены такие значения проектных параметров, при которых целевая функция имеет минимум (или максимум).
Слайд 4Задачи оптимизации.
Безусловная задача оптимизации состоит в отыскании максимума или минимума действительной
Условные задачи оптимизации, или задачи с ограничениями, — это такие, при формулировке которых задаются некоторые условия (ограничения) на множестве.
Слайд 5В результате ограничений область проектирова-ния а, определяемая всеми п проектными параметрами, может быть существенно
Слайд 6В ряде случаев из этих соотношений можно выразить одни проектные параметры
В рамках применения производных методы бывают : прямые методы оптимизации; градиент-ные методы; методы 2-го порядка и др.
Слайд 7 Одномерная оптимизация.
Одномерная задача оптимизации в общем
Найти наименьшее (или наибольшее) значение целевой функции у = f(x), заданной на множестве
и определить значение проектного параметра
при котором целевая функция принимает экстремальное значение.
Существование решения поставленной задачи вытекает из следующей теоремы:
Слайд 8Теорема Вейерштрасса.
Всякая функция f(x), непрерывная на отрезке
принимает на
значения, т. е. на отрезке
существуют такие точки
и
что для любого
имеют место неравенства
.
Слайд 9Многомерная оптимизация.
Метод нулевого порядка не берет в расчет производные минимизированной
Слайд 10Методы безусловной оптимизации.
Хука и Дживса (осуществление 2 видов поиска –
Минимизации по правильному симплексу (поиск точки минимума соответствующей функции посредством сравнения на каждой отдельной итерации ее значений в вершинах симплекса);
Циклического координатного спуска (использование в качестве ориентиров поиска координатных векторов);
Розенброка (основан на применении одномерной минимизации);
Минимизации по деформированному симплексу (модификация метода минимизации по правильному симплексу: добавление процедуры сжатия, растяжения).
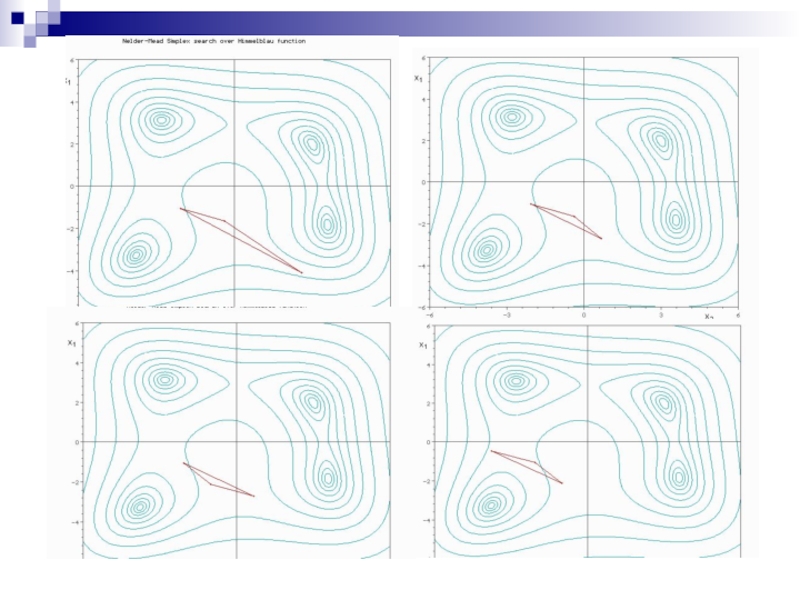
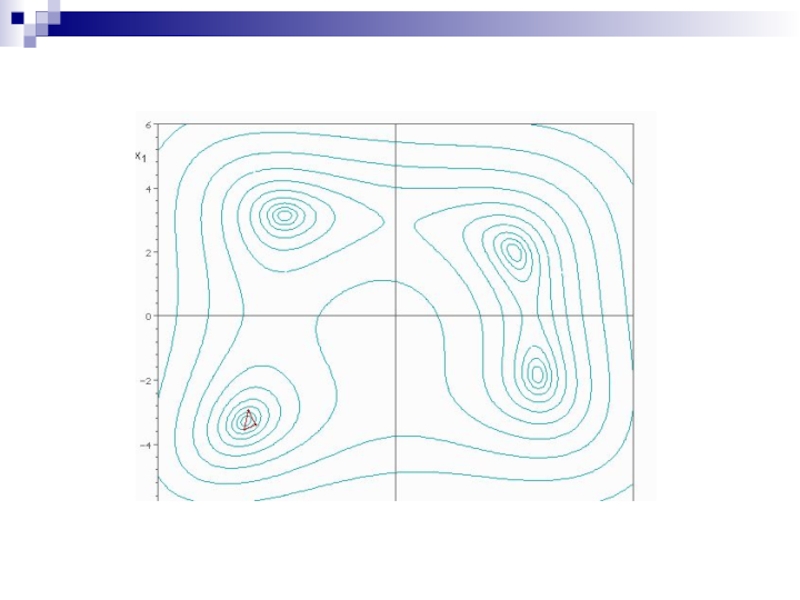
Слайд 11Метод Нелдера - Мида, также известный как метод деформируемого многогранника и симплекс-метод, метод безусловной
Суть метода заключается в последовательном переме-щении и деформировании симплекса вокруг точки экстремума.
Метод находит локальный экстремум и может «застрять» в одном из них. Если всё же требуется найти глобальный экстремум, можно пробовать выбирать другой начальный симплекс.
Метод Нелдера - Мида