- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы обработки экспериментальных данных презентация
Содержание
- 1. Методы обработки экспериментальных данных
- 2. Введение
- 3. Окружающий нас мир насыщен информацией… Ее НЕОБХОДИМО
- 4. Области применения анализа экспериментальных данных Химия Физика Биология Техника Технологии Гуманитарные науки Прочая деятельность
- 5. 1.2. Основные этапы анализа данных 1. Планирование
- 6. 1.3. Структуры данных Одномерные наборы данных (одна
- 7. 1.3. Структуры данных Количественные данные
- 8. 1.3. Структуры данных Источники данных Первичные Вторичные
- 9. 1.4. Что такое переменная? Переменная (английский термин
- 10. 1.4. Что такое переменная? Так как значения
- 11. 1.4. Что такое переменная? Медиана разбивает выборку
- 12. 1.5. Основные законы распределения случайных величин и
- 13. 1.5. Основные законы распределения случайных величин и
- 14. 1.5. Основные законы распределения случайных величин и
- 15. 1.5. Основные законы распределения случайных величин и
- 16. 1.5. Основные законы распределения случайных величин и
- 17. 1.5. Основные законы распределения случайных величин и
- 18. 1.5. Основные законы распределения случайных величин и
- 19. 1.6. Краткий обзор современных программных средств для
- 20. 1.6. Краткий обзор современных программных средств для
- 21. 1.6. Краткий обзор современных программных средств для
- 22. 1.6. Краткий обзор современных программных средств для
- 23. 1.6. Краткий обзор современных программных средств для
- 24. Вопросы ?
- 25. КЛАССИФИКАЦИЯ В РАСПОЗНАВАНИИ ОБРАЗОВ
- 26. Схема системы распознавания Система распознавания образов
- 27. Байесовская теория принятия решений при дискретных признаках
- 28. Байесовская теория принятия решений при дискретных признаках
- 29. Байесовская теория принятия решений при дискретных признаках Одномерный вариант Многомерный вариант
- 30. Байесовская теория принятия решений при непрерывных признаках
- 31. Байесовская теория принятия решений при непрерывных признаках Вероятность ошибки классификации при двух классах:
- 32. Идеи классификации Случай 1. Известны полностью
- 33. Идеи классификации Случай 2. Условные плотности
- 34. Идеи классификации Случай 3. Условные плотности
- 35. Идеи классификации Случай 4. Число классов
- 36. Прямые методы восстановления решающей функции
- 37. НЕЙРОННЫЕ СЕТИ: еще один подход к классификации
- 39. Интересные данные Тело клетки имеет размер 3
- 41. Персептроны
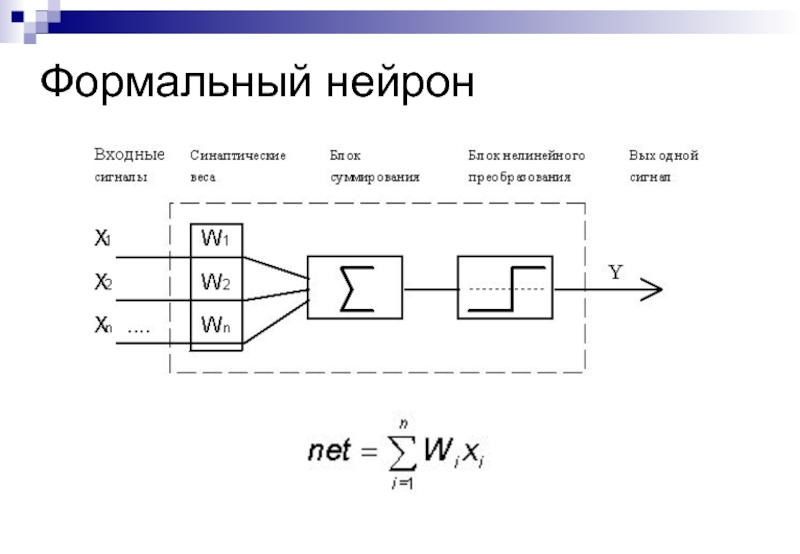
- 42. Формальный нейрон
- 43. Нелинейное преобразование Маккалок - Питтс Линейная Сигмоидальная
- 44. Перцептрон Розенблата Розенблат: нейронная сеть рассмотренной
- 45. Обучение сети Обучить нейронную сеть это значит,
- 46. Обучение перцептрона Начальные значения весов
- 47. STATISTICA Neural Networks
- 48. ВОПРОСЫ ?
- 49. ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА
- 50. Что такое планирование эксперимента Целью планирования
- 51. Эксперименты в науке и промышленности Экспериментальные
- 52. Общие идеи Обычно любая машина или
- 53. Общие идеи Пример 1: Производство красителей
- 54. Общие идеи Пример 2: Максимизация выхода
- 55. Общие идеи Пример 3: Улучшение поверхностной
- 56. Что такое планирование эксперимента Взвешивание трех
- 57. Построение линейной статической модели объекта Считаем,
- 58. Построение линейной статической модели объекта С
- 59. Построение линейной статической модели объекта В
- 60. Крутое восхождение по поверхности отклика В
- 61. Полный факторный эксперимент Полным факторным экспериментом
- 62. Полный факторный эксперимент С использованием ортогонального плана
- 63. Дробные реплики При большом числе входов объекта
- 64. Насыщенные планы. Симплекс Иногда исследователь ставит
- 65. Насыщенные планы. Симплекс Один из общих способов построения планов:
- 66. Насыщенные планы. Планы Плаккета – Бермана
- 67. Разбиение матрицы планирования на блоки При
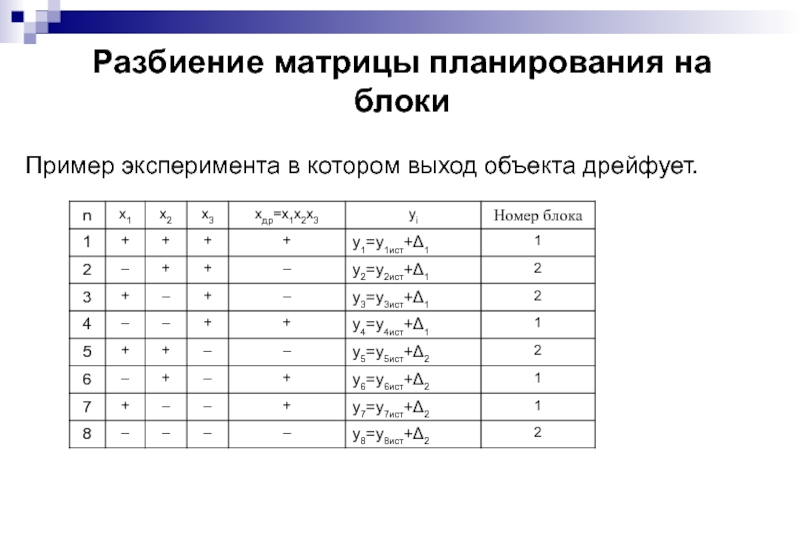
- 68. Разбиение матрицы планирования на блоки Пример эксперимента в котором выход объекта дрейфует.
- 69. Разбиение матрицы планирования на блоки Для
- 70. Обработка результатов эксперимента 1. Проверка однородности
- 71. Обработка результатов эксперимента 2. Проверка адекватности модели.
- 72. Обработка результатов эксперимента 3. Проверка значимости
- 73. Обработка результатов эксперимента 4. Интерпретация модели.
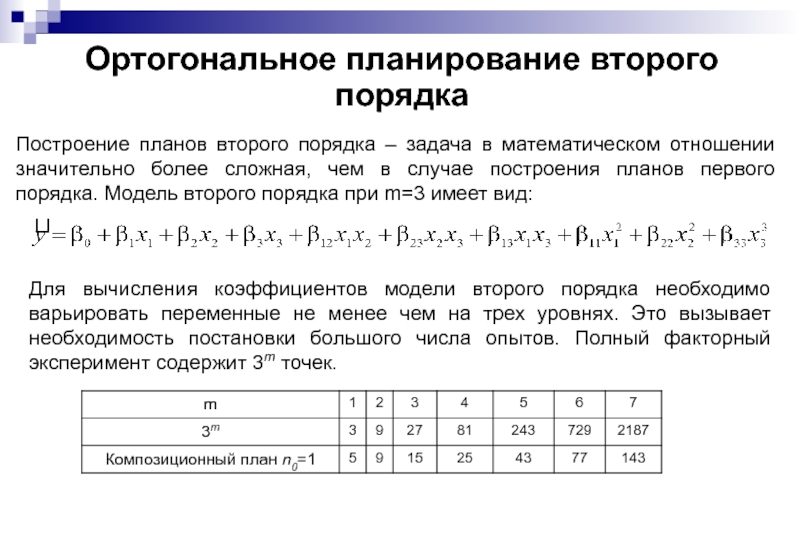
- 74. Ортогональное планирование второго порядка Построение планов
- 75. Ортогональное планирование второго порядка В 1951
- 76. Ортогональное планирование второго порядка Пример композиционного
- 77. Ротатабельное планирование Если эта дисперсия одинакова
- 78. Метод случайного баланса Часто влияние факторов на
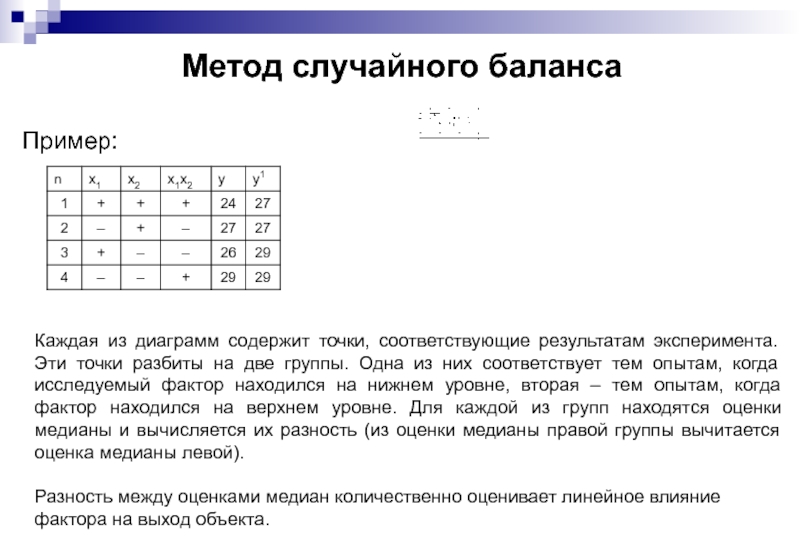
- 79. Метод случайного баланса Пример: Каждая из диаграмм
- 80. ВОПРОСЫ ?
- 81. МЕТОДЫ НЕПАРАМЕТРИЧЕСКОЙ ОБРАБОТКИ ИНФОРМАЦИИ
- 82. Оценивание функционалов Необходимо по выборке x1,…,xn случайной
- 83. Оценивание функционалов Схема построения оценки Фn следующая.
- 84. Простейшие оценки функции и плотности распределения вероятности
- 85. Простейшие оценки функции и плотности распределения вероятности
- 86. Простейшие оценки функции и плотности распределения вероятности
- 87. Простейшие оценки функции и плотности распределения вероятности
- 88. Полиграммы Повысим степень гладкости оценки fn(x) по
- 89. Полиграммы Для улучшения сглаживающих свойств оценки плотности построены полиграммы более высоких порядков:
- 90. Метод "К ближайших соседей" Считаем, что для
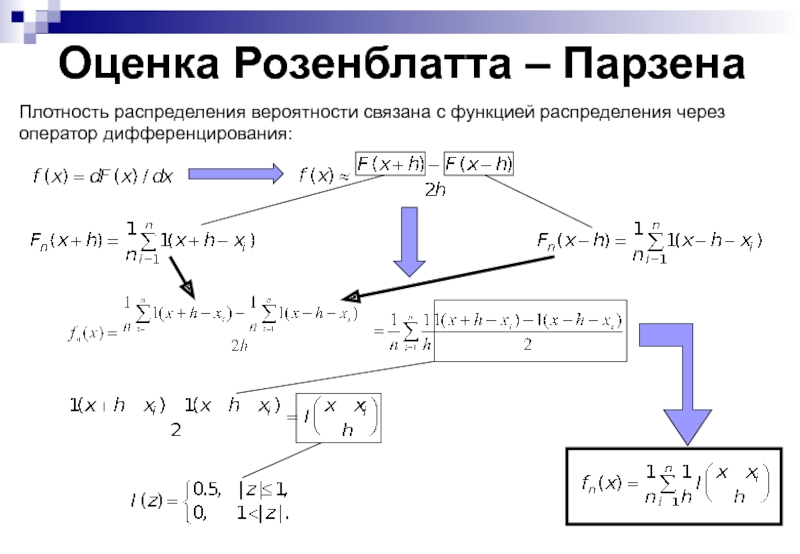
- 91. Оценка Розенблатта – Парзена Плотность распределения вероятности
- 92. Оценка Розенблатта – Парзена Степень гладкости оценки
- 93. Оценка Розенблатта – Парзена Многомерный случай:
- 94. Оценка условной плотности вероятности Рассматриваем объект, имеющий
- 95. Оценка регрессии Регрессией называют первый начальный условный
- 96. Оценка регрессии Подбор оптимального параметра коэффициента размытости
- 97. Оценка регрессии Возьмем теперь другое крайнее состояние
- 98. Оценка регрессии Рекуррентный расчет оценки регрессии. Для
- 99. Оценка регрессии Инверсная модель. Для объекта с
- 100. Робастные оценки регрессии В реальной ситуации исходные
- 101. Робастные оценки регрессии Запишем критериальную форму получения оценки:
- 102. Робастные оценки регрессии Модульный критерий не является
- 103. Адаптивное управление при априорной неопределенности Адаптацией природа
- 104. ВОПРОСЫ ?
- 105. ДИСПЕРСИОННЫЙ АНАЛИЗ
- 106. Постановка проблемы Дисперсионный анализ является статистическим методом
- 107. Однофакторный дисперсионный анализ Предположим, что анализируется влияние
- 108. Однофакторный дисперсионный анализ Рассмотрим оценки различных дисперсий,
- 109. Если
- 110. Двухфакторный дисперсионный анализ Рассмотренный ранее однофакторный дисперси-онный
- 111. Двухфакторный дисперсионный анализ Пусть результаты эксперимента представлены таблицей:
- 112. Если
- 113. Для оценки влияния взаимодействия факторов AB вычисляем
- 114. Планирование эксперимента при дисперсионном анализе Дисперсионный анализ
- 115. Планирование эксперимента при дисперсионном анализе Такие способы
- 116. Планирование эксперимента при дисперсионном анализе Схема расчетов
- 117. Планирование эксперимента при дисперсионном анализе Перейдем теперь
- 118. ВОПРОСЫ ?
- 119. АНАЛИЗ ТРЕНДОВ И ВРЕМЕННЫХ РЯДОВ
- 120. Введение Временные ряды отличаются от обычных данных
- 121. Введение ПРИМЕР. Чтобы составить бюджет на следующий
- 122. Анализ трендов и сезонности Анализ трендов и
- 123. Анализ трендов и сезонности
- 124. Анализ трендов и сезонности Тренд и циклический
- 125. Анализ трендов и сезонности Сезонный индекс: среднее
- 126. Анализ трендов и сезонности Затем, чтобы устранить
- 127. Анализ трендов и сезонности Поправка на сезон:
- 128. Анализ трендов и сезонности Долгосрочный тренд и
- 129. Анализ трендов и сезонности Прогноз: тренд с
- 130. Моделирование циклического поведения с помощью ARIMA-процессов Бокса-Дженкинса
- 131. Моделирование циклического поведения с помощью ARIMA-процессов Бокса-Дженкинса
- 132. Моделирование циклического поведения с помощью ARIMA-процессов Бокса-Дженкинса
- 133. Моделирование циклического поведения с помощью ARIMA-процессов Бокса-Дженкинса
- 134. Моделирование циклического поведения с помощью ARIMA-процессов Бокса-Дженкинса
- 135. Моделирование циклического поведения с помощью ARIMA-процессов Бокса-Дженкинса
- 136. Моделирование циклического поведения с помощью ARIMA-процессов Бокса-Дженкинса
- 137. ВОПРОСЫ ?
- 138. ИДЕНТИФИКАЦИЯ СТАТИЧЕСКИХ МОДЕЛЕЙ ОБЪЕКТОВ
- 139. Общие понятия Идентификация – это процесс построения
- 140. Постановка задачи подстройки параметров нелинейных моделей
- 141. Критерий наименьших квадратов При равноточных измерениях
- 142. Критерий наименьших квадратов то критерий наименьших
- 143. Метод наименьших квадратов при линейной параметризации модели
- 144. Метод наименьших квадратов при линейной параметризации модели Пример расчета параметров:
- 145. Метод последовательной линеаризации при подстройке параметров на
- 146. Робастные оценки параметров Параметры модели (которые являются
- 147. Простейший адаптивный алгоритм подстройки параметров Линейная
- 148. Простейший адаптивный алгоритм подстройки параметров Нелинейная
- 149. ВОПРОСЫ ?
- 150. ИДЕНТИФИКАЦИЯ И АДАПТИВНОЕ УПРАВЛЕНИЕ ДИНАМИЧЕСКИМИ ОБЪЕКТАМИ
- 151. Дискретные динамические модели стохастических объектов В
- 152. Дискретные динамические модели стохастических объектов Считаем, что объект описывается дискретным уравнением: Модель имеет вид:
- 153. Дискретные динамические модели стохастических объектов Если объект имеет вид: То оптимальная модель имеет вид:
- 154. Подстройка параметров с использованием функций чувствительности
- 155. Подстройка параметров с использованием функций чувствительности
- 156. Применение простейшего адаптивного алгоритма Рассчитаем параметры
- 157. Применение простейшего адаптивного алгоритма В каждый
- 158. Применение простейшего адаптивного алгоритма Рассмотрим нелинейную
- 159. Адаптивные системы обработки информации В адаптивных
- 160. Постановка задачи адаптивного управления Рассматриваем адаптивную
- 161. Примеры синтеза устройств управления для простейших линейных
- 162. Примеры синтеза устройств управления для простейших линейных
- 163. Синтез алгоритмов управления для линейных систем Объект:
- 164. Алгоритмы адаптивного управления для нелинейных систем Объект описывается нелинейным разностным уравнением:
- 165. Управление динамическими системами с чистыми запаздываниями
- 166. Управление динамическими системами с чистыми запаздываниями
- 167. ВОПРОСЫ ?
Слайд 3Окружающий нас мир насыщен информацией…
Ее НЕОБХОДИМО обрабатывать для принятия управленческих решений.
Существует
НО ЕСТЬ проблема…. понимание и интерпретация результатов!
НЕОБХОДИМО ЗНАТЬ И ПОНИМАТЬ КАК И ЧТО ПРОИСХОДИТ ВНУТРИ МАТ. ПАКЕТОВ!
1.1. Введение
Слайд 4Области применения анализа экспериментальных данных
Химия
Физика
Биология
Техника
Технологии
Гуманитарные науки
Прочая деятельность
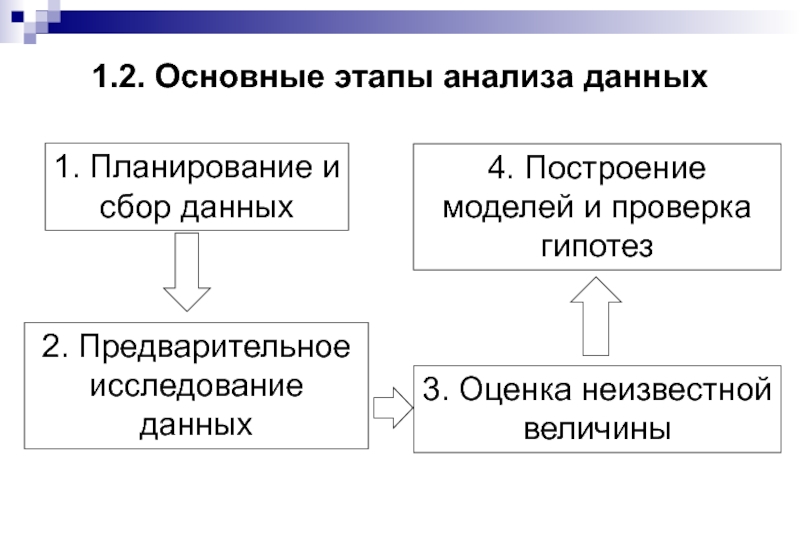
Слайд 51.2. Основные этапы анализа данных
1. Планирование и сбор данных
2. Предварительное
3. Оценка неизвестной величины
4. Построение моделей и проверка гипотез
Слайд 61.3. Структуры данных
Одномерные наборы данных (одна переменная) содержат только один признак,
Двумерные наборы данных содержат информацию о двух признаках для каждого из объектов. В дополнение к обобщению свойств каждой из этих двух переменных, рассматриваемых как отдельные наборы одномерных данных,
Наборы многомерных данных содержат информацию о трех или более признаках для каждого объекта. В дополнение к обобщению свойств каждой из этих переменных (рассматриваемых как отдельные наборы одномерных данных) и установлению зависимости между парами переменных (как при анализе набора двумерных данных)
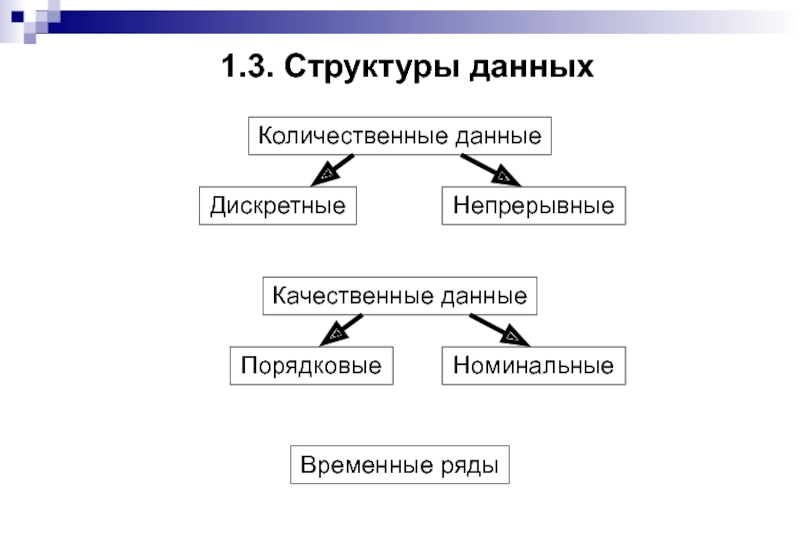
Слайд 71.3. Структуры данных
Количественные данные
Дискретные
Непрерывные
Качественные данные
Порядковые
Номинальные
Временные ряды
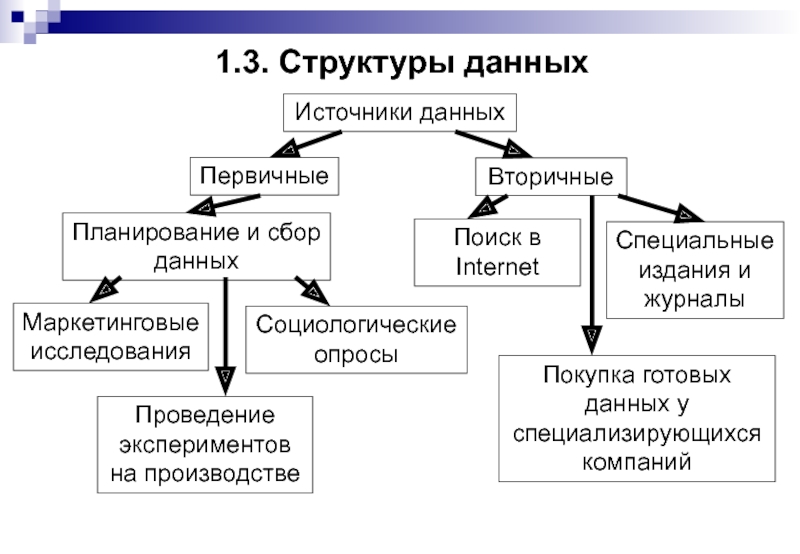
Слайд 81.3. Структуры данных
Источники данных
Первичные
Вторичные
Планирование и сбор данных
Маркетинговые исследования
Социологические опросы
Проведение экспериментов на
Поиск в Internet
Специальные издания и журналы
Покупка готовых данных у специализирующихся компаний
Слайд 91.4. Что такое переменная?
Переменная (английский термин variable) — это то, что
ПРИМЕРЫ: анкетные данные, систолическое давление пациентов, количество лейкоцитов в крови, цена акций, товаров, услуг, потребление, инвестиции, доход, государственные закупки товаров и услуг, инструмент государственного регулирования (в экономике); рейтинг программ, доля зрителей, количество посещений сайта (в рекламе); скорость, температура, объем, масса в (физике) и т. д.
Слайд 101.4. Что такое переменная?
Так как значения переменных не постоянны, нужно научиться
Для этого придуманы описательные или дескриптивные статистики.
Минимум и максимум — это минимальное и максимальное значения переменной.
Среднее — сумма значений переменной, деленная на n (число значений переменной).
Дисперсия и стандартное отклонение — наиболее часто используемые меры изменчивости переменной. Дисперсия меняется от нуля до бесконечности. Крайнее значение 0 означает отсутствие изменчивости, когда значения переменной постоянны.
Слайд 111.4. Что такое переменная?
Медиана разбивает выборку на две равные части. Половина
Медиана дает общее представление о том, где сосредоточены значения переменной, иными словами, где находится ее центр. В некоторых случаях, например при описании доходов населения, медиана более удобна, чем среднее.
Мода представляет собой максимально часто встречающееся значение переменной (иными словами, наиболее «модное" значение переменной), например популярная передача на телевидении, модный цвет платья или марка автомобиля и т. д.
А так же есть еще множество других статистик: квартили, коэффициент асимметрии, эксцесс, коэффициент корреляции и др.
Слайд 121.5. Основные законы распределения случайных величин и их назначение
Законы распределения случайных
Слайд 131.5. Основные законы распределения случайных величин и их назначение
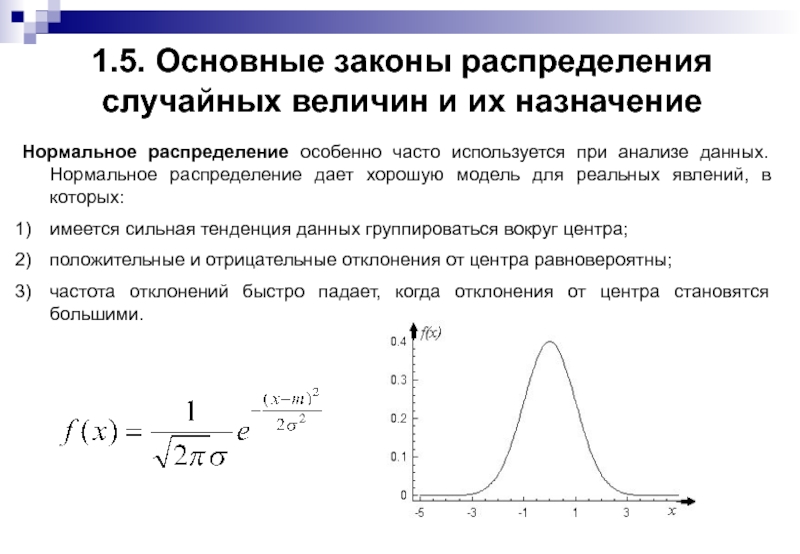
Нормальное распределение особенно
имеется сильная тенденция данных группироваться вокруг центра;
положительные и отрицательные отклонения от центра равновероятны;
частота отклонений быстро падает, когда отклонения от центра становятся большими.
Слайд 141.5. Основные законы распределения случайных величин и их назначение
Равномерное распределение полезно
Слайд 151.5. Основные законы распределения случайных величин и их назначение
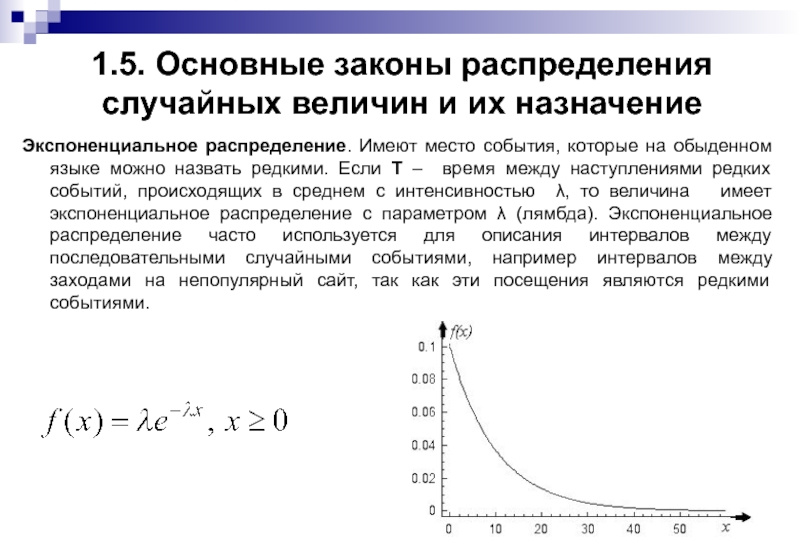
Экспоненциальное распределение. Имеют
Слайд 161.5. Основные законы распределения случайных величин и их назначение
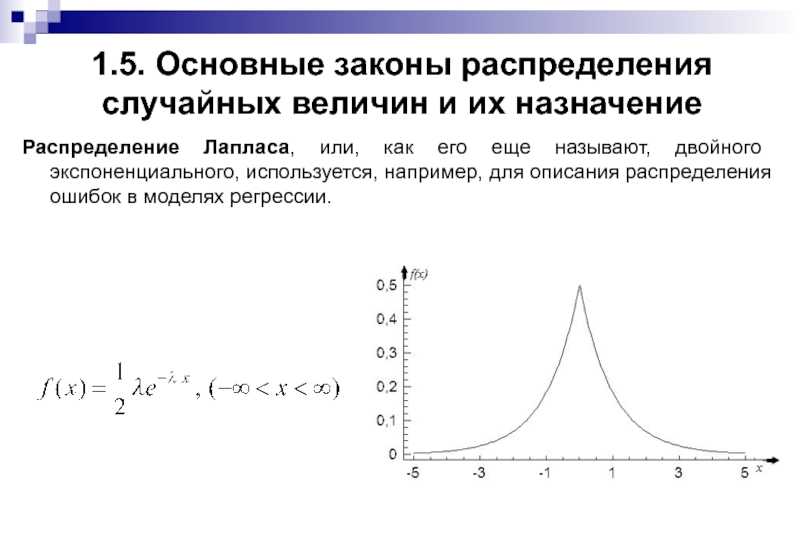
Распределение Лапласа, или,
Слайд 171.5. Основные законы распределения случайных величин и их назначение
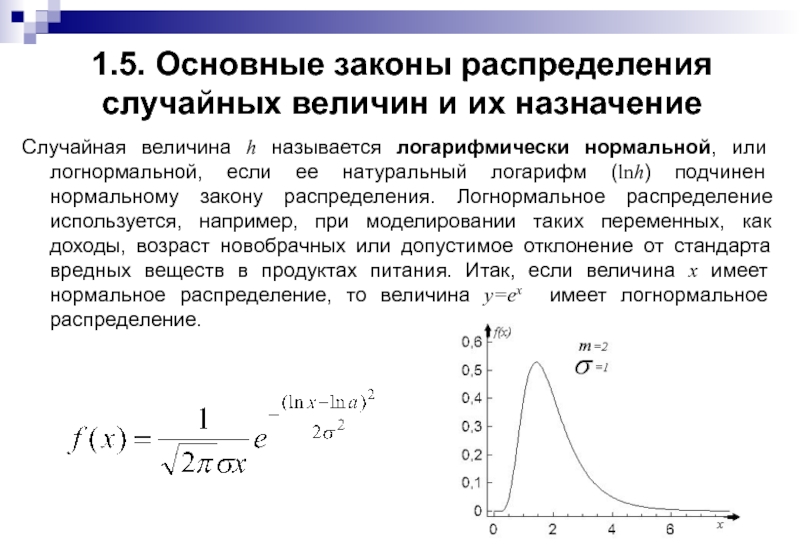
Случайная величина h
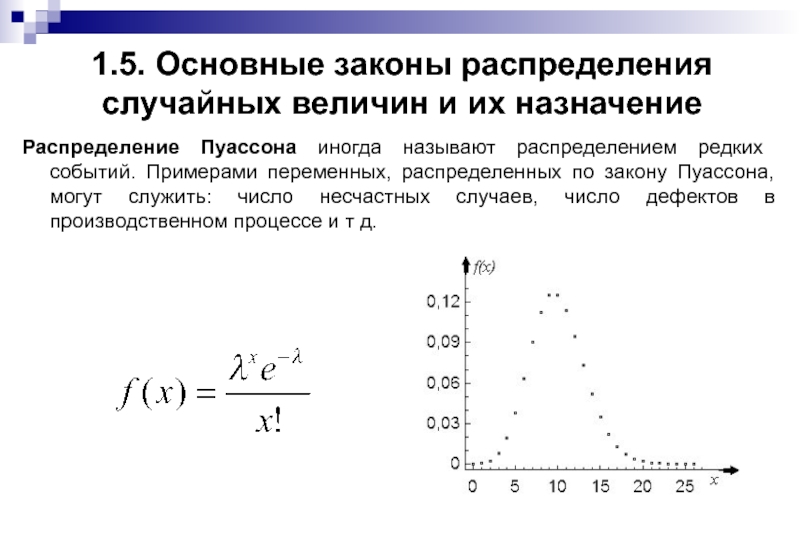
Слайд 181.5. Основные законы распределения случайных величин и их назначение
Распределение Пуассона иногда
Слайд 191.6. Краткий обзор современных программных средств для проведения анализа данных.
MATLAB –
• математические вычисления
• создание алгоритмов
• моделирование
• анализ данных, исследования и визуализация
• научная и инженерная графика
• разработка приложений, включая создание графического интерфейса
Слайд 201.6. Краткий обзор современных программных средств для проведения анализа данных.
Mathcad –
В среде Mathcad доступны более сотни операторов и логических функций, предназначенных для численного и символьного решения математических задач различной сложности и применения этих функций для анализа данных.
Слайд 211.6. Краткий обзор современных программных средств для проведения анализа данных.
STATISTICA –
С помощью реализованных в системе STATISTICA мощных языков программирования, снабженных специальными средствами поддержки, легко создаются законченные пользовательские решения и встраиваются в различные другие приложения или вычислительные среды.
Слайд 221.6. Краткий обзор современных программных средств для проведения анализа данных.
Deductor
Аналитическая платформа
Слайд 231.6. Краткий обзор современных программных средств для проведения анализа данных.
STATGRAPHICS –
StatAdvisor дает пользователям понятные разъяснения полученных результатов, определяет, являются ли эти результаты существенными, и обращает особое внимание на любые возможные ошибки в анализе. Пользователи получают немедленную интерпретацию результатов в процедурах, доступных в как основной системе, так и в четырех специальных модулях, поставляемых по выбору: Quality Control (контроль качества), Experimental Design (планирование эксперимента), Time-Series Analysis (анализ временных рядов) и Advanced Multivariate Method (анализ вариаций).
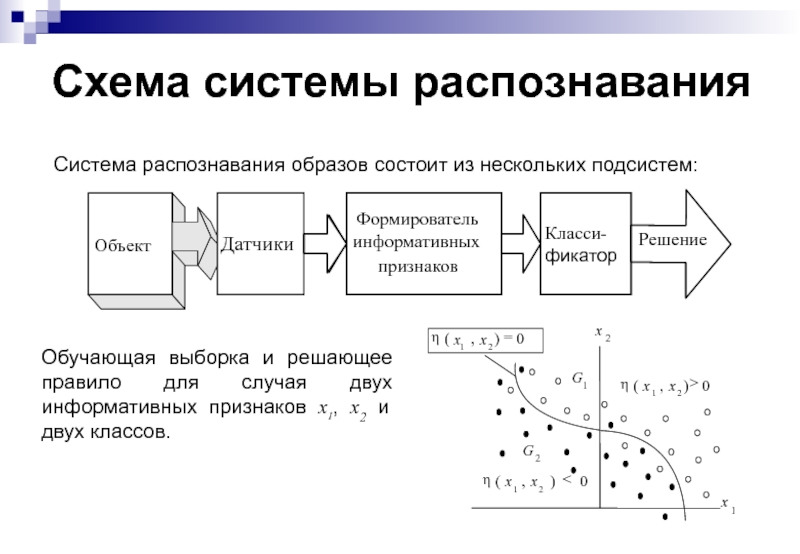
Слайд 26Схема системы распознавания
Система распознавания образов состоит из нескольких подсистем:
Обучающая
Слайд 27Байесовская теория принятия решений
при дискретных признаках
Одномерный вариант
Рассматриваем m классов (полную
По формуле Байеса вычисляем апостериорные вероятности для всех рассматриваемых классов:
Выносим решение об истинности того класса (с номером ν), для которого апостериорная вероятность максимальная:
Слайд 28Байесовская теория принятия решений
при дискретных признаках
Многомерный вариант
Для простоты считаем, что
X принимает возможные значения x1,…,xn1, Y принимает возможные значения y1,…,yn2.
По формуле Байеса вычисляем апостериорные вероятности для всех рассматриваемых классов:
Выносим решение об истинности того класса (с номером ν), для которого апостериорная вероятность максимальная:
Слайд 29Байесовская теория принятия решений
при дискретных признаках
Одномерный вариант
Многомерный вариант
Слайд 30Байесовская теория принятия решений
при непрерывных признаках
Одномерны вариант:
Апостериорные вероятности классов
если
то принимается решение о 1-м классе, иначе о 2-м классе.
Слайд 31Байесовская теория принятия решений
при непрерывных признаках
Вероятность ошибки классификации при
Слайд 32Идеи классификации
Случай 1. Известны полностью условные плотности распределения вероятности для
Двумерный случай
Одномерный случай
Слайд 33Идеи классификации
Случай 2. Условные плотности распределения вероятности для признаков известны
Неизвестные параметры θ1 и θ2 доопределяются с помощью одного из методов математической статистики, например с помощью метода максимального правдоподобия, на основе обучающей выборки.
Дальнейшая классификация проводится, как и в случае 1.
По обучающей выборке доопределяются и априорные вероятности:
Слайд 34Идеи классификации
Случай 3. Условные плотности распределения вероятности неизвестны, но известна
Вариант 1. Восстанавливается решающая функция.
Вариант 2. По обучающей выборке восстанавливаются условные плотности
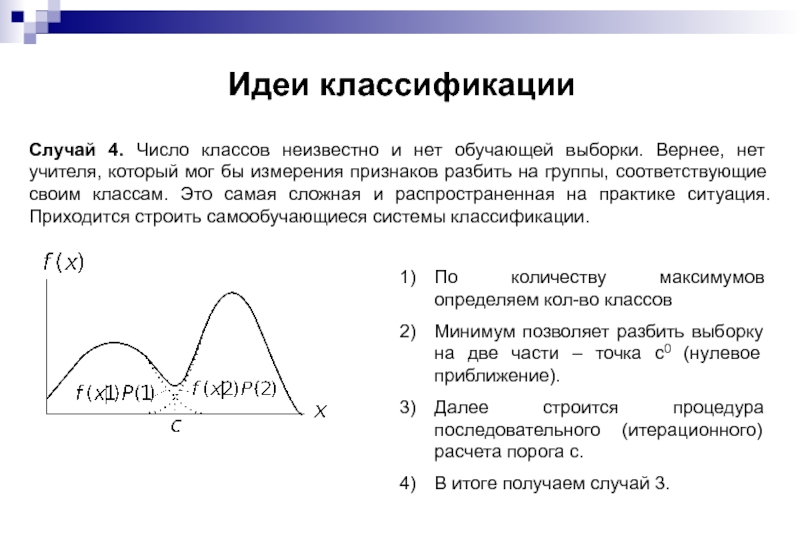
Слайд 35Идеи классификации
Случай 4. Число классов неизвестно и нет обучающей выборки.
По количеству максимумов определяем кол-во классов
Минимум позволяет разбить выборку на две части – точка c0 (нулевое приближение).
Далее строится процедура последовательного (итерационного) расчета порога c.
В итоге получаем случай 3.
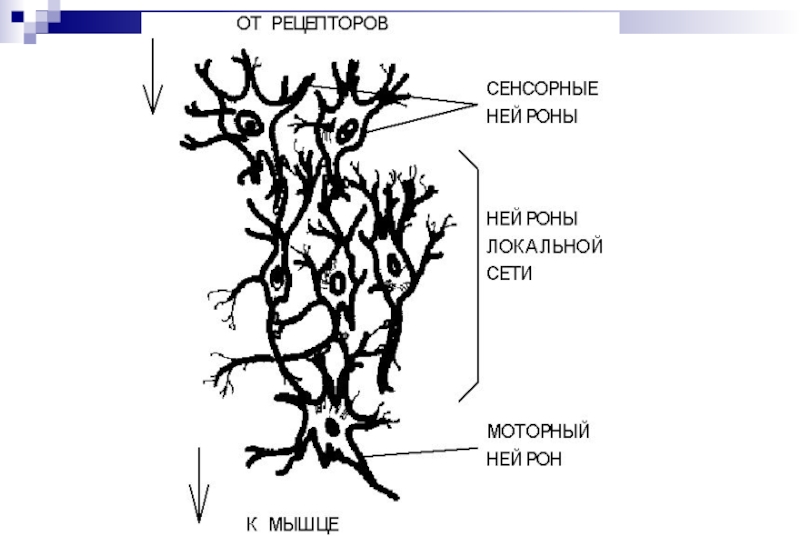
Слайд 37НЕЙРОННЫЕ СЕТИ: еще один подход к классификации
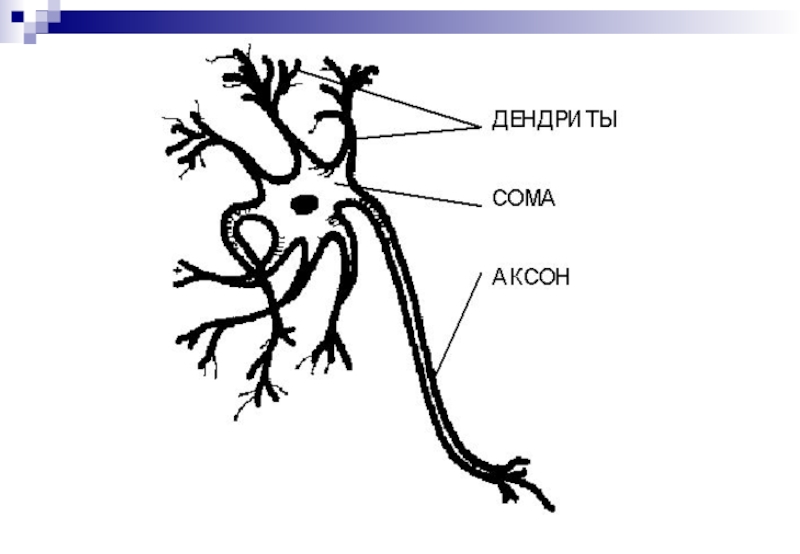
Идея взята из биологии:
Клетка -
Нейрон - элемент клеточной структуры мозга
Нейрон осуществляет прием и передачу информации в виде импульсов нервной активности
Природа импульсов - электрохимическая
Слайд 39Интересные данные
Тело клетки имеет размер 3 - 100 микрон
Гигантский аксон кальмара
Потенциал, превышающий 50 мВ изменяет проводимость мембраны аксона
Общее число нейронов в ЦНС человека порядка 100.000.000.000
Каждая клетка связана в среднем с 10.000 других нейронов
Совокупность в объеме 1 мм*3 - независимая локальная сеть
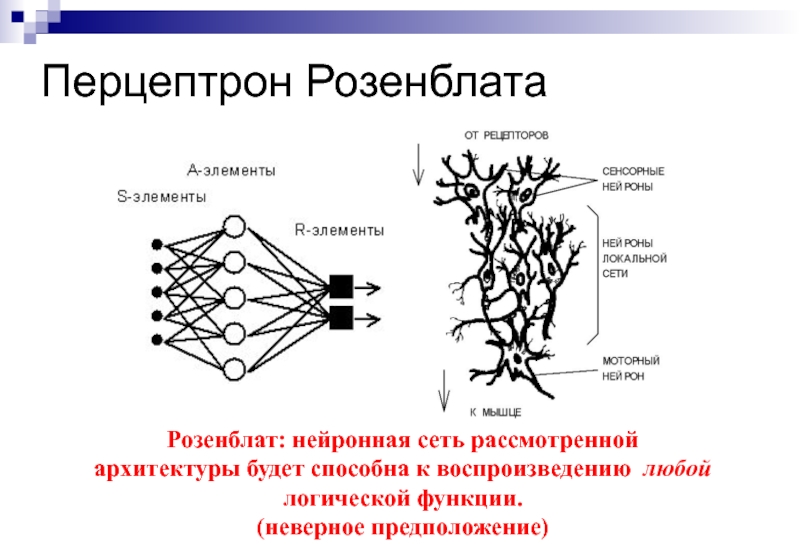
Слайд 44Перцептрон Розенблата
Розенблат: нейронная сеть рассмотренной
архитектуры будет способна к воспроизведению любой
логической
(неверное предположение)
Слайд 45Обучение сети
Обучить нейронную сеть это значит, сообщить ей, чего от нее
Показав ребенку изображение буквы и получив неверный ответ, ему сообщается тот, который хотят получить.
Ребенок запоминает этот пример с верным ответом и в его памяти происходят изменения в нужном направлении.
Слайд 46Обучение перцептрона
Начальные значения весов всех нейронов полагаются случайными.
Слайд 50Что такое планирование эксперимента
Целью планирования эксперимента является создание таких планов
Выход объекта состоит из неизвестного сигнала (функции от входов) и центрированной помехи
Слайд 51Эксперименты в науке и промышленности
Экспериментальные методы широко используются как в
Обычно основная цель научного исследования состоит в том, чтобы показать статистическую значимость эффекта воздействия определенного фактора на изучаемую зависимую переменную.
В условиях промышленного эксперимента основная цель обычно заключается в извлечении максимального количества объективной информации о влиянии изучаемых факторов на производственный процесс с помощью наименьшего числа дорогостоящих наблюдений.
Слайд 52Общие идеи
Обычно любая машина или станок, используемый на производстве, позволяет
Слайд 53Общие идеи
Пример 1: Производство красителей для ткани. Рассмотрим эксперимент по
Результаты эксперимента показали, что имеется три наиболее важных фактора: Полисульфидный индекс, Время и Температура. Эту информацию теперь можно использовать для более тонкой настройки аппаратуры, что бы улучшить качество красителя.
Слайд 54Общие идеи
Пример 2: Максимизация выхода химической реакции. Выход продукта многих
Формально цель эксперимента заключается в том, чтобы найти оптимальное положение на поверхности выхода, образованной двумя переменными: временем и температурой.
Слайд 55Общие идеи
Пример 3: Улучшение поверхностной однородности при производстве кремниевых кристаллов.
Слайд 56Что такое планирование эксперимента
Взвешивание трех тел по традиционной схеме ("+"
Взвешивание трех тел с использованием планирования эксперимента.
Видно, что при новой схеме взвешивания дисперсия веса объектов получается вдвое меньше, чем при традиционном методе взвешивания, хотя
в обоих случаях выполнялось по четыре опыта.
Слайд 57Построение линейной статической модели объекта
Считаем, что входами объекта являются u1,…,um,
Необходимо на основе эксперимента (на основе нескольких измерений входов и выхода объекта) вычислить коэффициенты модели.
Экспериментальные точки для входных координат зададим в вершинах гиперпрямоугольника.
Интервалы покачивания относительно базовой точки задаются экспериментатором, и они определяют область изучения объекта.
Слайд 58Построение линейной статической модели объекта
С целью унификации процедур построения планов,
Точки плана в вершинах прямоугольника в новых координатах оказываются в вершинах квадрата с единичными координатами. Центр плана переходит в начало координат.
В итоге получается план:
Слайд 59Построение линейной статической модели объекта
В новых безразмерных координатах x1,…,xm линейная
Параметры βi модели рассчитаем по критерию наименьших квадратов :
Предполагая, что измерения выхода некоррелированные и равноточные получаем систему линейных алгебраических уравнений:
Слайд 60Крутое восхождение по поверхности отклика
В планировании эксперимента поверхностью отклика называют
В 1951 году Бокс и Уилсон предложили использовать последовательный "шаговый" метод движения к экстремуму выхода объекта.
Коэффициенты αi линейной модели являются оценками составляющих градиента:
Далее движение осуществляется по поверхности отклика в направлении оценки градиента
, где k - величина шага.
Слайд 61Полный факторный эксперимент
Полным факторным экспериментом называется эксперимент, в котором реализуются
При построении линейной модели объекта используется полный факторный эксперимент типа 2m. Условия эксперимента записываются в таблицы, в которых строки соответствуют различным опытам, а столбцы – значениям факторов. Такие таблицы называются матрицами планирования эксперимента.
Слайд 62Полный факторный эксперимент
С использованием ортогонального плана первого порядка можно определять не
Например, при m=2 можно рассчитать и коэффициенты модели:
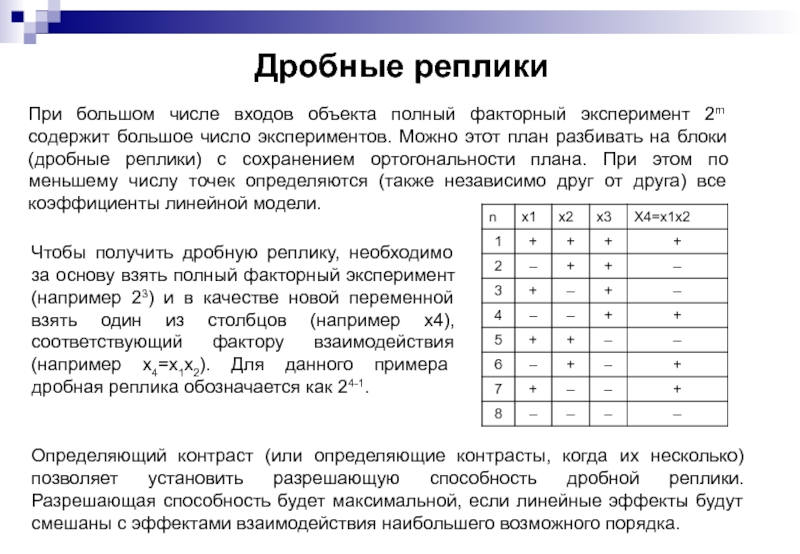
Слайд 63Дробные реплики
При большом числе входов объекта полный факторный эксперимент 2m содержит
Чтобы получить дробную реплику, необходимо за основу взять полный факторный эксперимент (например 23) и в качестве новой переменной взять один из столбцов (например x4), соответствующий фактору взаимодействия (например x4=x1x2). Для данного примера дробная реплика обозначается как 24-1.
Определяющий контраст (или определяющие контрасты, когда их несколько) позволяет установить разрешающую способность дробной реплики. Разрешающая способность будет максимальной, если линейные эффекты будут смешаны с эффектами взаимодействия наибольшего возможного порядка.
Слайд 64Насыщенные планы. Симплекс
Иногда исследователь ставит цель получения линейного уравнения модели
Ортогональный план проводится в вершинах правильного симплекса. Правильным симплексом называется выпуклая правильная фигура в многомерном пространстве, число вершин которой превышает размерность этого пространства на единицу.
Эти планы центральные и ортогональные.
Слайд 66Насыщенные планы.
Планы Плаккета – Бермана
Плаккет и Берман в 1946 г.
Задаются базовые строки. Каждая следующая строка матрицы планирования образуется из исходной циклическим сдвигом вправо. Получается матрица размером m x m. Последняя (m+1) -я строка матрицы планирования состоит из минус единиц.
Пример базисных строк:
Слайд 67Разбиение матрицы планирования на блоки
При проведении эксперимента выход объекта дрейфует.
В качестве примера рассмотрим ортогональный план 23 . Считаем, что выход объекта имеет аддитивный дрейф на величину Δ1 (когда проводятся эксперименты с номерами 1, 2, 3, 4) и на величину Δ2 (когда проводятся эксперименты № 5, 6, 7, 8). Этот дрейф приводит к смещению на величину (4Δ1-4 Δ2)/8 параметра β3.
Слайд 68Разбиение матрицы планирования на блоки
Пример эксперимента в котором выход объекта
Слайд 69Разбиение матрицы планирования на блоки
Для устранения этого недостатка изменим порядок
Слайд 70Обработка результатов эксперимента
1. Проверка однородности дисперсий. Если при реализации ортогонального
Проверка однородности дисперсий производится с помощью различных статистик. Простейшей из них является статистика Фишера, представляющая собой отношение наибольшей из оценок к наименьшей:
Так же можно выполнить проверку с использованием статистики Кочрена:
Слайд 71Обработка результатов эксперимента
2. Проверка адекватности модели. Вычисляем остаточную сумму квадратов ,
На основе дополнительного эксперимента объема n0 в одной из точек плана (например в центре плана) строим оценку для дисперсии выхода объекта. Число степеней свободы для оценки n0 -1. По статистике Фишера проверяем гипотезу о равенстве дисперсий, которая совпадает с гипотезой об адекватности модели.
Если статистика не превосходит порогового значения, то принимается гипотеза об адекватности модели. В противоположном случае эта гипотеза отвергается. Надо заново строить модель, например, усложняя ее за счет введения дополнительных факторов, либо отказываться от линейной модели и переходить к квадратичной модели.
Слайд 72Обработка результатов эксперимента
3. Проверка значимости коэффициентов заключается в проверке гипотезы
Вычисляется статистика Стьюдента:
Если |t|
Слайд 73Обработка результатов эксперимента
4. Интерпретация модели. Производится качественное сопоставление поведения полученной
Если характер связи между входами и выходом объекта на основе построенной модели не соответствует реальным связям (на базе информации от экспертов) в объекте, то такую модель надо поставить под сомнение либо полностью отказаться от нее.
Слайд 74Ортогональное планирование второго порядка
Построение планов второго порядка – задача в
Для вычисления коэффициентов модели второго порядка необходимо варьировать переменные не менее чем на трех уровнях. Это вызывает необходимость постановки большого числа опытов. Полный факторный эксперимент содержит 3m точек.
Слайд 75Ортогональное планирование второго порядка
В 1951 году Бокс и Уилсон предложили
Точки на осях координат называют звездными точками. Их количество равно удвоенному числу факторов. Расстояние от центра плана до звездной точки одинаково. Его обозначают буквой α и называют звездным плечом.
Композиционные планы имеют следующие положительные свойства:
1. Они могут быть получены в результате достройки планов первого порядка.
2. Дополнительные точки на осях координат и в центре плана не нарушают ортогональности для столбцов, соответствующих факторам xj и эффектам взаимодействия xixj .
Слайд 76Ортогональное планирование второго порядка
Пример композиционного плана:
С учетом новых переменных xl’
Слайд 77Ротатабельное планирование
Если эта дисперсия одинакова на равном удалении от центра
Ортогональный план первого порядка является ротатабельным.
Построение ротатабельного плана второго порядка из симплексных планов:
Слайд 78Метод случайного баланса
Часто влияние факторов на выходную координату объекта имеет затухающий
В 1956 году Сатерзвайт предложил метод случайного баланса для отсеивания небольшого числа значимых факторов на шумовом поле. Метод базируется на постановке экспериментов по плану, содержащему координаты точек, выбранных случайным образом.
Построение матрицы планирования осуществляют следующим образом. Все факторы разбивают на группы. Затем для каждой группы строят матрицы планирования, беря за основу полный факторный эксперимент или дробные реплики. План проведения эксперимента образуется путем случайного смешивания строк соответствующих базовых планов (для групп факторов). Полученный план реализуется на объекте, и результаты анализируются с помощью диаграмм рассеяния.
Слайд 79Метод случайного баланса
Пример:
Каждая из диаграмм содержит точки, соответствующие результатам эксперимента. Эти
Разность между оценками медиан количественно оценивает линейное влияние фактора на выход объекта.
Слайд 82Оценивание функционалов
Необходимо по выборке x1,…,xn случайной величины X найти оценку функционала
Рассмотрим некоторые примеры функционалов:
– дисперсия.
– приведенная энтропия.
– математическое ожидание.
Слайд 83Оценивание функционалов
Схема построения оценки Фn следующая. Вначале строится оценка для плотности
Основным свойством оценки Фn(x1,…,xn) является ее состоятельность. Оценка Фn функционала Ф называется состоятельной, если:
Оценка Фn параметра Ф называется несмещенной, если:
Требование состоятельности определяет практическую пригодность оценок, ибо в противоположном случае (при несостоятельности оценок) увеличение объема исходной выборки не будет приближать оценку к "истинной" величине. По этой причине свойство состоятельности должно проверяться в первую очередь.
Она является асимптотически несмещенной, если:
Слайд 84Простейшие оценки функции
и плотности распределения вероятности
По упорядоченной независимой выборке x1,…,xn
где 1(z) – единичная функция:
Слайд 85Простейшие оценки функции
и плотности распределения вероятности
Так как плотность распределения f(x)
Можно получить оценку для плотности распределения :
Здесь δ(x-xi) – дельта-функция Дирака. Она имеет "игольчатый" ("гребенчатый") вид: уходит до ∞ в точке xi , а при остальных значениях аргумента x равна нулю и обладает свойствами:
- площадь под дельта функцией единичная.
селектирующее свойство дельта-функции позволяет легко выполнять интегрирование. Интеграл оказывается равным подынтегральному выражению, стоящему перед дельта-функцией, в особой точке.
Слайд 86Простейшие оценки функции
и плотности распределения вероятности
Первое свойство показывает, что, несмотря
Второе селектирующее свойство дельта-функции позволяет легко выполнять интегрирование. Интеграл оказывается равным подынтегральному выражению, стоящему перед дельта-функцией, в особой точке.
Оценка плотности распределения является несмещенной, но несостоятельной. В явном виде её использовать нельзя. Ею удобно пользоваться при вычислении оценок моментов (математического ожидания, дисперсии и др.) для случайной величины или для аналитической функции случайной величины. Получаемые оценки являются состоятельными и часто несмещенными.
Слайд 87Простейшие оценки функции
и плотности распределения вероятности
Многомерный случай:
Кратные измерения. При кратных
Слайд 88Полиграммы
Повысим степень гладкости оценки fn(x) по сравнению с простейшей оценкой функции
Она строится на выборочных интервалах, ограниченных выборочными значениями упорядоченной выборки x1,…,xn. Площадь каждого прямоугольника равна 1/(n-1)
Слайд 89Полиграммы
Для улучшения сглаживающих свойств оценки плотности построены полиграммы более высоких порядков:
Слайд 90Метод "К ближайших соседей"
Считаем, что для одномерной случайной величины X имеется
Многомерный случай:
Слайд 91Оценка Розенблатта – Парзена
Плотность распределения вероятности связана с функцией распределения через
Слайд 92Оценка Розенблатта – Парзена
Степень гладкости оценки плотности зависит от степени гладкости
Здесь h – коэффициент размытости ядра. Примеры треугольного, параболического и кубического ядер приведены ниже:
Слайд 94Оценка условной плотности вероятности
Рассматриваем объект, имеющий случайный вход (либо несколько входов)
Слайд 95Оценка регрессии
Регрессией называют первый начальный условный момент
Это некоторая усредненная количественная
Получим оценку регрессии:
Слайд 96Оценка регрессии
Подбор оптимального параметра коэффициента размытости для оценки регрессии. Перейдем от
При β=0 ядро K(·) не зависит от x.
Оценка регрессии равна среднему арифметическому выборочных значений выхода объекта для любых x.
Слайд 97Оценка регрессии
Возьмем теперь другое крайнее состояние для β: β=1. Оценка регрессии
Оптимальный параметр β лежит в интервале [0; 1].
Слайд 98Оценка регрессии
Рекуррентный расчет оценки регрессии. Для каждого фиксированного x на основе
Слайд 99Оценка регрессии
Инверсная модель. Для объекта с одним входом X и одним
и получаем оценку инверсной регрессии:
Слайд 100Робастные оценки регрессии
В реальной ситуации исходные экспериментальные данные xi, yi могут
Кроме математического ожидания случайной величины Y есть другая характеристика среднего положения – медиана. Медиана – это среднее по вероятности значение. Состоятельная оценка медианы представляет собой среднее по номеру значение в упорядоченной выборке:
Слайд 102Робастные оценки регрессии
Модульный критерий не является единственным для получения робастных оценок.
Некоторые виды функций F(v):
Слайд 103Адаптивное управление при априорной неопределенности
Адаптацией природа наделила все живое. Она представляет
Свойством адаптации человек наделил и созданные им устройства. Управление в этих устройствах осуществляется таким образом, чтобы как можно быстрее и лучше нейтрализовать влияние непредвиденных изменений или приспособиться к ним.
Слайд 106Постановка проблемы
Дисперсионный анализ является статистическим методом анализа результатов наблюдений, зависящих от
Методами дисперсионного анализа устанавливается наличие влияния заданного фактора на изучаемый процесс (на выходную переменную процесса) за счёт статистической обработки наблюдаемой совокупности выборочных данных.
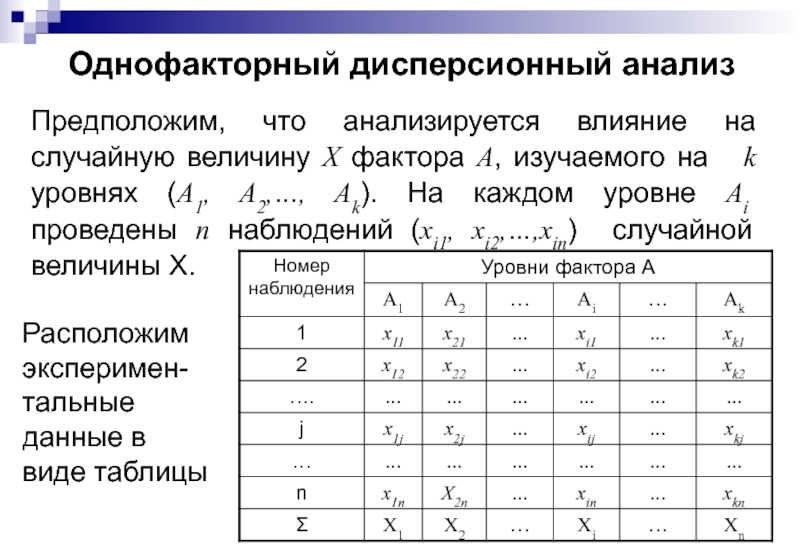
Слайд 107Однофакторный дисперсионный анализ
Предположим, что анализируется влияние на случайную величину X фактора
Расположим эксперимен-тальные данные в виде таблицы
Слайд 108Однофакторный дисперсионный анализ
Рассмотрим оценки различных дисперсий, возникающие при анализе таблицы результатов
Из предпосылок дисперсионного анализа следует, что должно иметь место равенство всех дисперсий. При выполнении этого условия находим оценку дисперсии, характеризующей рассеяние значений xij вне влияния фактора A, по формуле:
Слайд 109Если
Сравниваем и устанавливаем наличие влияния фактора A.
Однофакторный дисперсионный анализ
Для упрощения вычислений приведем алгоритм их выполнения. Вычисляем последовательно суммы:
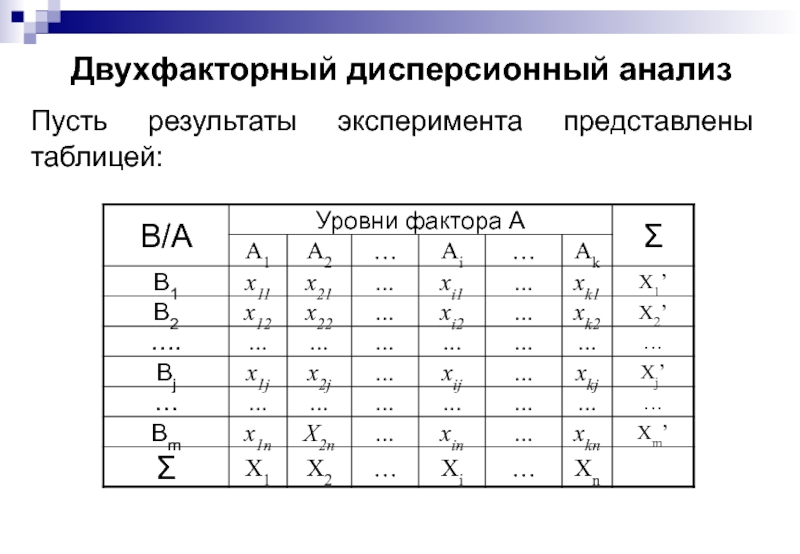
Слайд 110Двухфакторный дисперсионный анализ
Рассмотренный ранее однофакторный дисперси-онный анализ обладает информативностью, не большей,
Рассмотрим случай, когда анализируется влияние одновременно двух факторов A и B.
Слайд 112Если
Двухфакторный дисперсионный анализ
Дисперсионный анализ для двухфакторных таблиц проводится в следующей последовательности. Вычисляются суммы:
Далее находятся оценки дисперсий:
Если , то влияние фактора B признается значимым.
Слайд 113Для оценки влияния взаимодействия факторов AB вычисляем дополнительную сумму:
Двухфакторный дисперсионный анализ
Приведенный
Далее анализ проводится, как и ранее, с той лишь разницей, что в клетках таблицы вместо отдельных значений используется их средние значения. Вычисляется оценка дисперсии и проверяется значимость взаимодействия факторов:
Слайд 114Планирование эксперимента при дисперсионном анализе
Дисперсионный анализ тесно связан с соответствующим планированием
Если на результат эксперимента действуют одновременно несколько факторов, то наилучший эффект дает одновременный дисперсионный анализ всех этих факторов (многофакторный анализ).
Методы дисперсионного анализа позволяют исследовать и такой случай, когда некоторые сочетания уровней пропущены. Такой эксперимент называется дробным факторным экспериментом (ДФЭ). Планирование при ДФЭ приобретает особо важную роль, ибо пропущенные сочетания уровней не так-то просто нейтрализовать.
Слайд 115Планирование эксперимента при дисперсионном анализе
Такие способы планирования существуют и притом не
Слайд 116Планирование эксперимента при дисперсионном анализе
Схема расчетов для латинского квадрата очень похожа
Находим сумму квадратов по столбцам, деленную на число наблюдений в столбце:
Находим сумму квадратов итогов по строкам, деленную на число наблюдений в строке:
Находим квадрат общего итога, деленный на число всех наблюдений:
Находим сумму квадратов итогов по уровням фактора C, деленную на число уровней:
Слайд 117Планирование эксперимента при дисперсионном анализе
Перейдем теперь к вычислению и оценке значимости
Если отличие будет значимым, то
Если отличие будет значимым, то
Слайд 120Введение
Временные ряды отличаются от обычных данных об одном временном срезе в
Теперь чтобы охарактеризовать совокупность данных в целом, уже недостаточно знать лишь типичное значение этих данных (среднее значение) или даже изменчивость этой совокупности данных (дисперсия). В этом случае желательно знать, что, скорее всего, произойдет дальше. НУЖЕН ПРОГНОЗ!
Слайд 121Введение
ПРИМЕР. Чтобы составить бюджет на следующий квартал, требуется достоверная оценка ожидаемого
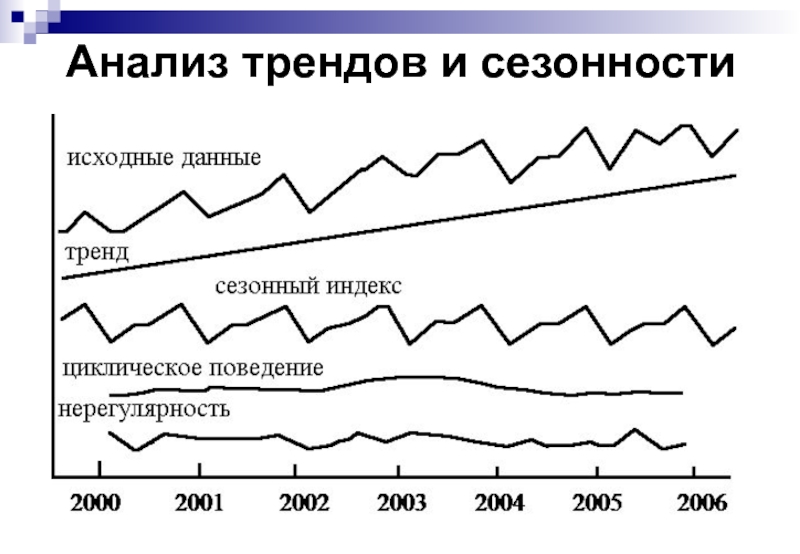
Слайд 122Анализ трендов и сезонности
Анализ трендов и сезонности представляет собой непосредственный, интуитивный
Базовая модель временного ряда представляет числа в этом ряде в виде произведения, получаемого путем умножения перечисленных компонентов.
Слайд 124Анализ трендов и сезонности
Тренд и циклический компонент: скользящее среднее
Скользящее среднее
Слайд 125Анализ трендов и сезонности
Сезонный индекс: среднее значение отношения к скользящему среднему
Чтобы выделить сезонное поведение, прежде всего, следует получить отношение исходных значений к скользящему среднему. Полученный результат будет включать сезонный и нерегулярный компоненты, поскольку скользящее среднее исключает из данных тренд и циклический компонент.
Слайд 126Анализ трендов и сезонности
Затем, чтобы устранить нерегулярный компонент, надо усреднить эти
Слайд 127Анализ трендов и сезонности
Поправка на сезон: деление ряда на сезонный индекс.
Поправка
Слайд 128Анализ трендов и сезонности
Долгосрочный тренд и прогноз с поправкой на сезонные
Когда временной ряд демонстрирует долгосрочную линейную тенденцию к нарастанию или снижению, для оценки этой тенденции и прогнозирования будущего можно воспользоваться регрессионным анализом.
Слайд 129Анализ трендов и сезонности
Прогноз: тренд с учетом сезонности
Чтобы прогнозировать будущее, надо
Слайд 130Моделирование циклического поведения с помощью ARIMA-процессов Бокса-Дженкинса
АRIМА-процессы Бокса-Дженкинса представляют собой семейство
ARIMA - сокращение от Autoregressive Integrated Moving Average
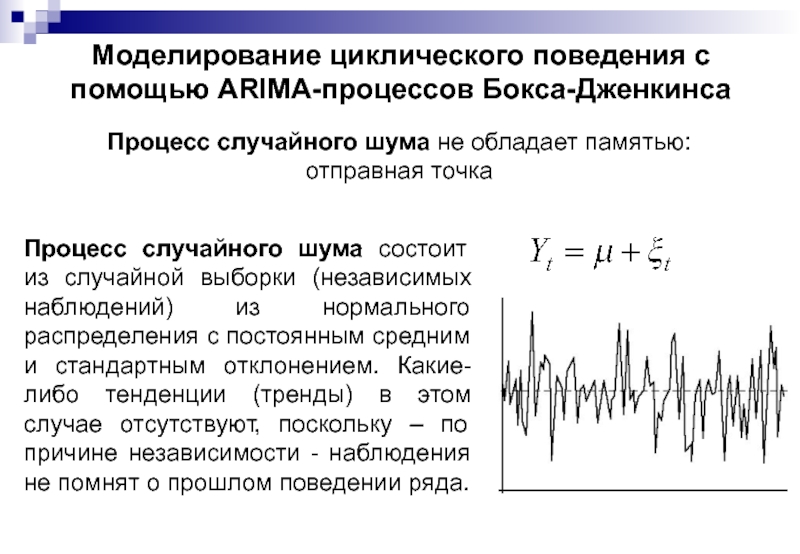
Слайд 131Моделирование циклического поведения с помощью ARIMA-процессов Бокса-Дженкинса
Процесс случайного шума не обладает
Процесс случайного шума состоит из случайной выборки (независимых наблюдений) из нормального распределения с постоянным средним и стандартным отклонением. Какие-либо тенденции (тренды) в этом случае отсутствуют, поскольку – по причине независимости - наблюдения не помнят о прошлом поведении ряда.
Слайд 132Моделирование циклического поведения с помощью ARIMA-процессов Бокса-Дженкинса
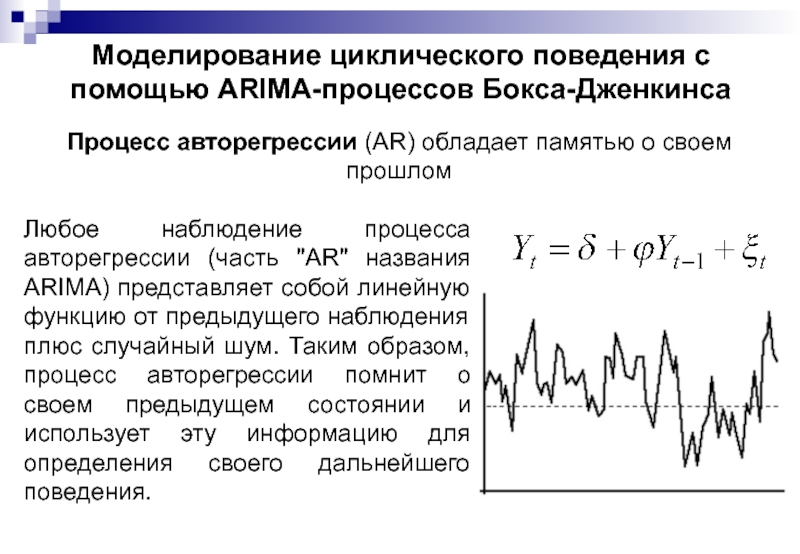
Процесс авторегрессии (AR) обладает памятью
Любое наблюдение процесса авторегрессии (часть "AR" названия ARIMA) представляет собой линейную функцию от предыдущего наблюдения плюс случайный шум. Таким образом, процесс авторегрессии помнит о своем предыдущем состоянии и использует эту информацию для определения своего дальнейшего поведения.
Слайд 133Моделирование циклического поведения с помощью ARIMA-процессов Бокса-Дженкинса
Процесс скользящего среднего (МА) имеет
Любое наблюдение процесса скользящего среднего состоит из константы, (долгосрочное среднее значение процесса), плюс независимый случайный шум минус часть предыдущего случайного шума. Процесс скользящего среднего не помнит в точности своего прошлого, но помнит компонент случайного шума того состояния, в котором он (процесс) находился. Таким образом, его память ограничена одним шагом в будущее; за пределами этого шага для процесса все начинается заново.
Слайд 134Моделирование циклического поведения с помощью ARIMA-процессов Бокса-Дженкинса
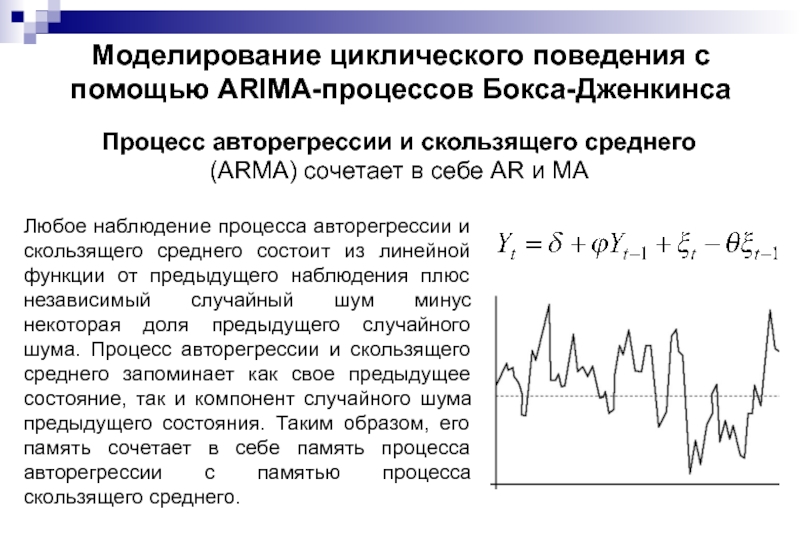
Процесс авторегрессии и скользящего среднего
Любое наблюдение процесса авторегрессии и скользящего среднего состоит из линейной функции от предыдущего наблюдения плюс независимый случайный шум минус некоторая доля предыдущего случайного шума. Процесс авторегрессии и скользящего среднего запоминает как свое предыдущее состояние, так и компонент случайного шума предыдущего состояния. Таким образом, его память сочетает в себе память процесса авторегрессии с памятью процесса скользящего среднего.
Слайд 135Моделирование циклического поведения с помощью ARIMA-процессов Бокса-Дженкинса
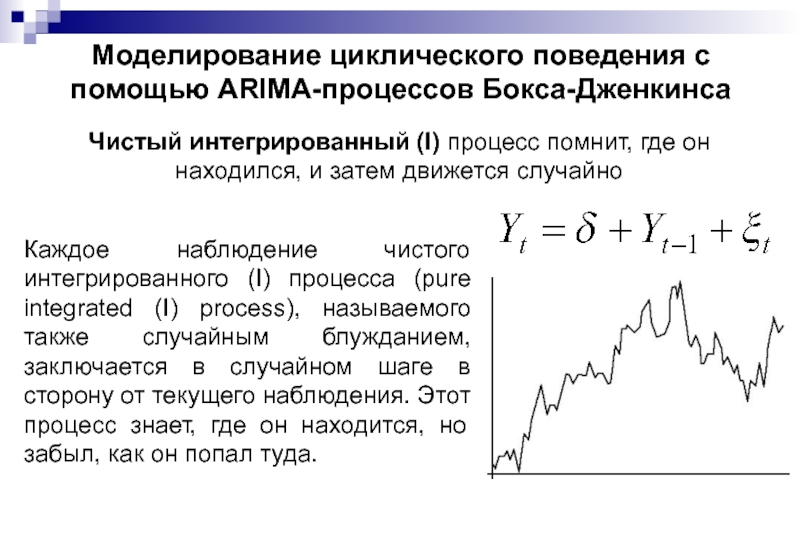
Чистый интегрированный (I) процесс помнит,
Каждое наблюдение чистого интегрированного (I) процесса (pure integrated (I) process), называемого также случайным блужданием, заключается в случайном шаге в сторону от текущего наблюдения. Этот процесс знает, где он находится, но забыл, как он попал туда.
Слайд 136Моделирование циклического поведения с помощью ARIMA-процессов Бокса-Дженкинса
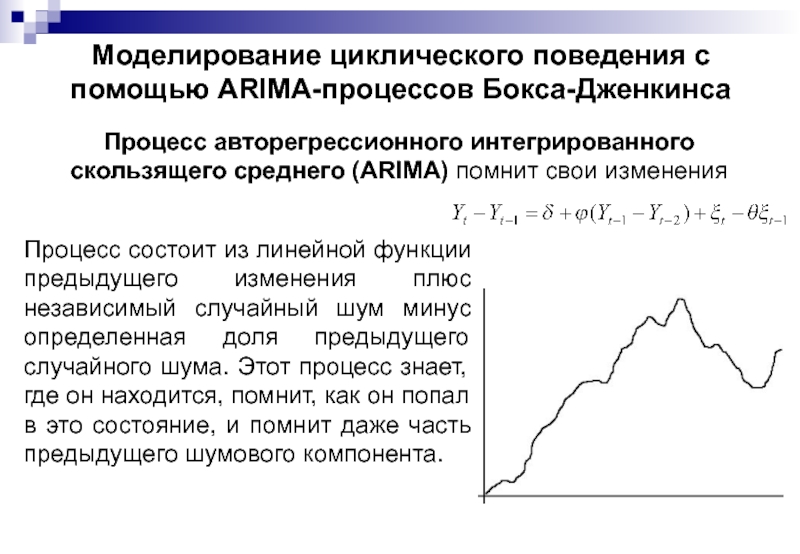
Процесс авторегрессионного интегрированного скользящего среднего
Процесс состоит из линейной функции предыдущего изменения плюс независимый случайный шум минус определенная доля предыдущего случайного шума. Этот процесс знает, где он находится, помнит, как он попал в это состояние, и помнит даже часть предыдущего шумового компонента.
Слайд 139Общие понятия
Идентификация – это процесс построения моделей объектов различной природы. Теория
Модели делятся на статические и динамические. Первые из них описывают объекты в стационарных режимах их работы. Динамические модели описывают переходные процессы в объектах, например, возникающие при переходе с одного стационарного режима работы объекта на другой.
Процесс идентификации складывается из двух взаимосвязанных этапов: идентификации структуры моделей и идентификации параметров в моделях выбранной структуры. При построении структуры модели (или набора конкурирующих либо взаимодополняющих структур) используется априорная информация об объекте. Для каждого класса объектов формируются банки структур с сопутствующей информацией.
Слайд 140Постановка задачи подстройки
параметров нелинейных моделей
Модель объекта берем в виде функции
Алгоритмы расчета будем строить, используя критерий наименьших квадратов и близкие к нему критерии, например наименьших модулей невязок. В зависимости от свойств помехи критерий наименьших квадратов приобретает различные формы – от простейшей до самой общей.
Считаем, что выход объекта состоит из полезного сигнала η(u, a) и центрированной помехи ξ.
Сигнальная часть выхода представляет собой известную функцию от входа с неизвестными параметрами a. В структуру функции η(u, a) . Все, что не удается описать в объекте, относят к помехе.
Слайд 141Критерий наименьших квадратов
При равноточных измерениях весовые коэффициенты 1/σi2, характеризующие информативность
Считаем, что в каждый момент времени ti (момент измерения входа и выхода объекта) помехи ξi, являются центрированными случайными величинами с дисперсиями σi2. Если дисперсии различны, то измерения называются неравноточными.
Тогда критерий наименьших квадратов имеет вид:
Слайд 142Критерий наименьших квадратов
то критерий наименьших квадратов базируется на элементах cij
Если все помехи ξi коррелированны, т. е:
Это общая форма критерия. Она включает в себя (при соответствующих упрощениях) все предыдущие формы. Запишем критерий в матричной форме.
Слайд 143Метод наименьших квадратов
при линейной параметризации модели
Модель объекта задана в виде
Параметры α находим по критерию наименьших квадратов:
Слайд 145Метод последовательной линеаризации
при подстройке параметров на основе критерия наименьших квадратов
Построим
Необходимое условие минимума приводит к системе линейных алгебраических уравнений:
Слайд 146Робастные оценки параметров
Параметры модели (которые являются оценками параметров объекта), полученные на
Так же существуют другие критерии вида:
Примеры функции ψ(e):
Слайд 147Простейший адаптивный алгоритм
подстройки параметров
Линейная параметризация модели:
На каждой итерации, например n
Каждому уравнению в пространстве параметров соответствует своя линия
Слайд 148Простейший адаптивный алгоритм
подстройки параметров
Нелинейная модель: На каждом шаге линеаризуем модель
В итоге получаем алгоритм перестройки параметров нелинейной модели:
Слайд 151Дискретные динамические модели
стохастических объектов
В динамическом режиме поведение объектов описывается различными
Дискретные модели привязаны к номерам дискретных моментов времени и поэтому основным аргументом для входных u(t) и выходных x(t), y(t) переменных является номер дискреты t = 0, 1, 2,…
Например:
Слайд 152Дискретные динамические модели
стохастических объектов
Считаем, что объект описывается дискретным уравнением:
Модель имеет вид:
Слайд 153Дискретные динамические модели
стохастических объектов
Если объект имеет вид:
То оптимальная модель имеет вид:
Слайд 154Подстройка параметров
с использованием функций чувствительности
Для примера рассмотрим модель:
Построим алгоритм расчета
Линеаризуем модель относительно параметров α(t-1) , вычисленных в предыдущий момент времени:
Здесь y(t|α(t-1)) – выход модели в момент времени t при значениях параметров, полученных в предыдущий момент времени t-1
ω(t) – вектор-столбец функций чувствительности выхода модели к параметрам модели.
Слайд 155Подстройка параметров
с использованием функций чувствительности
Функции чувствительности удовлетворяют уравнениям чувствительности:
Каждое
Для расчета параметров α(t) можно использовать, например, простейший адаптивный алгоритм:
Слайд 156Применение простейшего адаптивного алгоритма
Рассчитаем параметры линейных и нелинейных динамических моделей
Пример: Рассмотрим модель без обратной связи:
Функциями чувствительности выхода модели к ее параметрам являются измеренные значения выхода и входа объекта:
Слайд 157Применение простейшего адаптивного алгоритма
В каждый текущий момент времени t на
Слайд 158Применение простейшего адаптивного алгоритма
Рассмотрим нелинейную модель без обратной связи:
Алгоритм перестройки
Получаем следующие выход модели и функции чувствительности:
Слайд 159Адаптивные системы обработки информации
В адаптивных системах обработки информации и управления
Слайд 160Постановка задачи адаптивного управления
Рассматриваем адаптивную систему с идентификацией (АСИ). Синтезируем
Необходимо рассчитать управляющее воздействие u(t) , обеспечивающее достижение следующей цели: наименьшего уклонения выхода системы x от заданной траектории x* в каждый текущий момент времени.
Считаем, что поведение объекта в динамическом режиме описывается разностным уравнением:
Обозначим через y(k|α(t)) выход модели в момент времени k при значении вектора параметров α(t), вычисленных в момент времени. Если шум – белый, то
Слайд 161Примеры синтеза устройств управления
для простейших линейных систем
Формируем модель объекта:
Пример 1.
Находим параметры:
Из локального квадратичного критерия оптимальности
Рассчитываем оптимальное управление:
Слайд 162Примеры синтеза устройств управления
для простейших линейных систем
Модель объекта:
Пример 2. Объект
Параметры:
Находим управляющее воздействие :
Слайд 164Алгоритмы адаптивного управления
для нелинейных систем
Объект описывается нелинейным разностным уравнением:
Слайд 165Управление динамическими системами
с чистыми запаздываниями
Рассматриваем объект, описываемый разностным уравнением:
Строим
Выход модели находим из критерия наименьших квадратов:
Решение получается в форме