- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Метод следа презентация
Содержание
Дан куб ABCDA1B1C1D1. Необходимо провести сечение через точки M, N и L, лежащие на его рёбрах.
Слайд 2
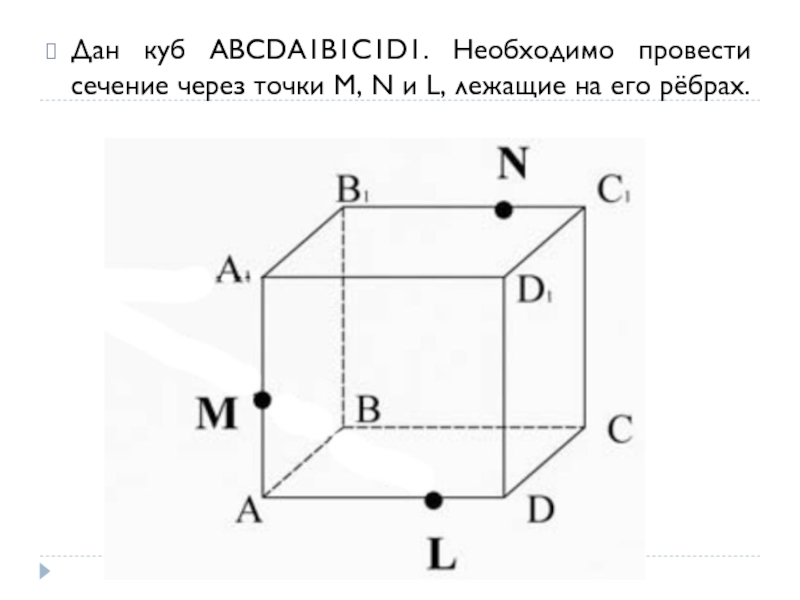
Дан куб ABCDA1B1C1D1. Необходимо провести сечение через точки M, N и
L, лежащие на его рёбрах.
Слайд 3
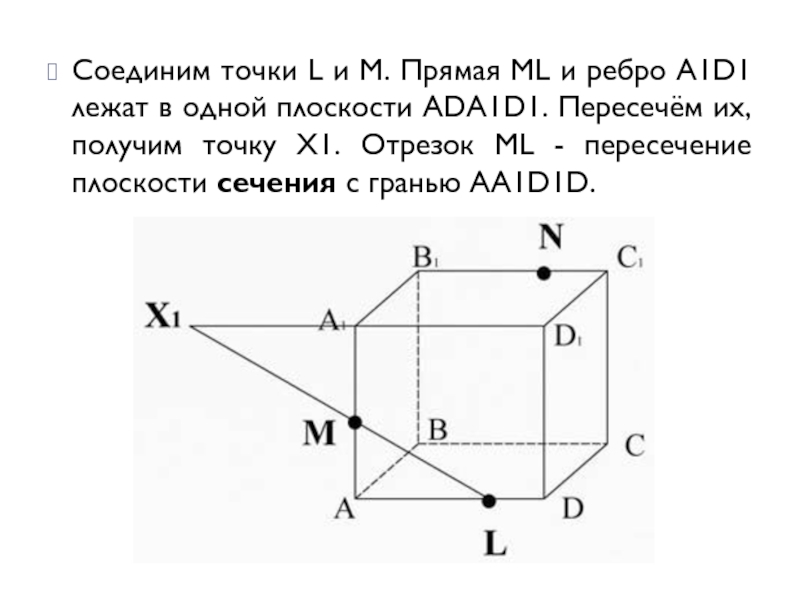
Соединим точки L и M. Прямая ML и ребро A1D1 лежат
в одной плоскости ADA1D1. Пересечём их, получим точку X1. Отрезок ML - пересечение плоскости сечения с гранью AA1D1D.
Слайд 4
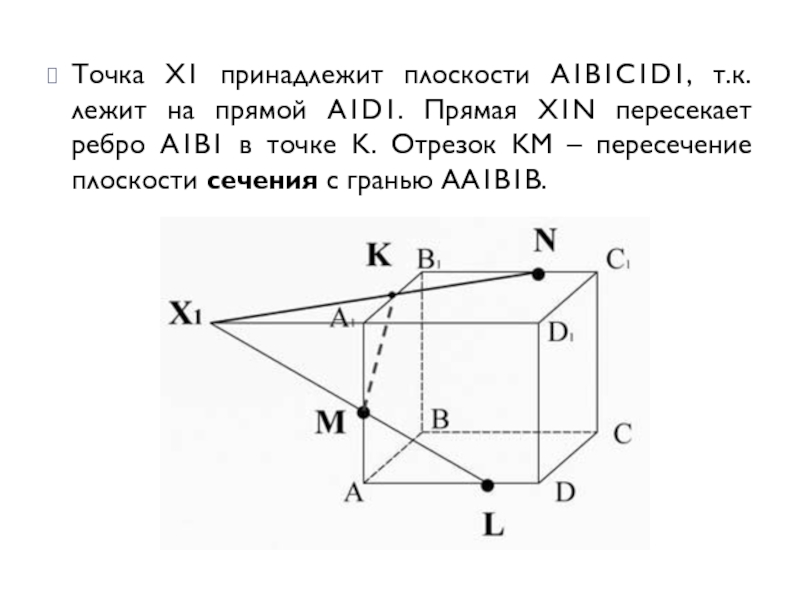
Точка X1 принадлежит плоскости A1B1C1D1, т.к. лежит на прямой A1D1. Прямая
X1N пересекает ребро A1B1 в точке K. Отрезок KM – пересечение плоскости сечения с гранью AA1B1B.
Слайд 5
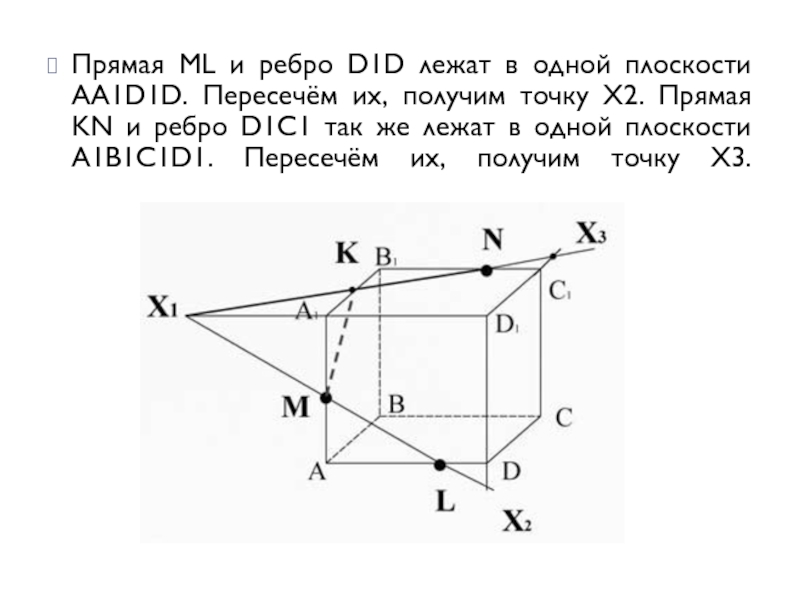
Прямая ML и ребро D1D лежат в одной плоскости AA1D1D. Пересечём
их, получим точку X2. Прямая KN и ребро D1C1 так же лежат в одной плоскости A1B1C1D1. Пересечём их, получим точку X3.
Слайд 6
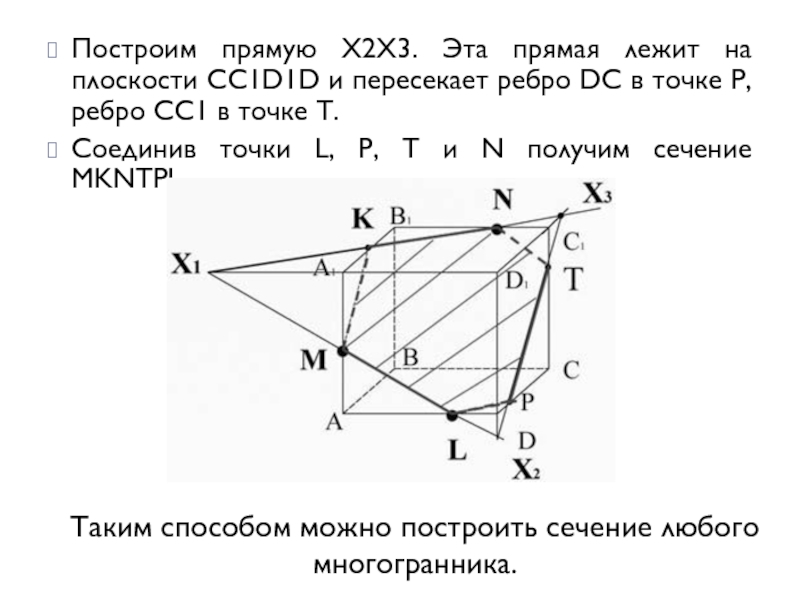
Построим прямую X2X3. Эта прямая лежит на плоскости CC1D1D и пересекает
ребро DC в точке P, ребро СС1 в точке T.
Соединив точки L, P, T и N получим сечение MKNTPL.
Соединив точки L, P, T и N получим сечение MKNTPL.
Таким способом можно построить сечение любого многогранника.
