- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Метод поиска в глубину. (Лекция 5) презентация
Содержание
- 1. Метод поиска в глубину. (Лекция 5)
- 2. Поиск в глубину (Depth-first search, DFS)
- 3. Процедура Поиск(u) Поиск (u) { цвет
- 4. Процедура Поиск_в_графе Поиск_в_графе() { для ∀u ∈
- 5. Анализ Общее число операций при выполнении Поиск_в_графе:
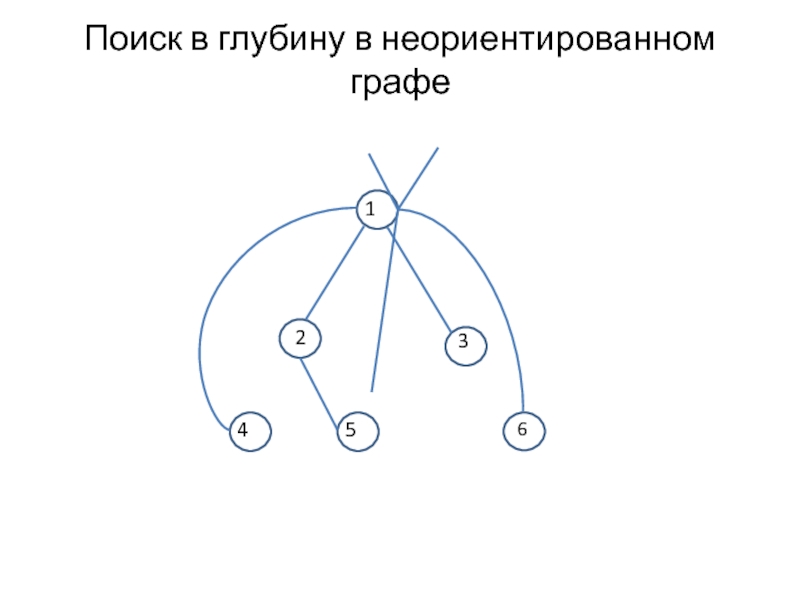
- 6. Поиск в глубину в неориентированном графе
- 7. Глубинный остовный лес Поиск в глубину на
- 8. Свойства поиска в глубину Времена обнаружения и
- 9. Теорема При поиске в глубину в графе
- 10. Поиск в глубину в ориентированном графе
- 11. Поиск в глубину в ориентированном графе G
- 12. Решение задачи топологической сортировки методом поиска в
- 13. Пример Трусы Носки Штаны Ремень Ботинки Рубашка
- 14. Поиск компонент связности в графе Компонента связности
- 15. Реализация поиска компонент связности в графе Поиск
- 16. Метод поиска в ширину (BFS, Breadth-first search)
- 17. Алгоритм Инициализация для ( ∀u ∈
- 18. пока (Q ≠ ∅) выполнить { u
- 19. Использование очереди В качестве промежуточной структуры
- 20. Нахождение кратчайшего пути в лабиринте 1 2
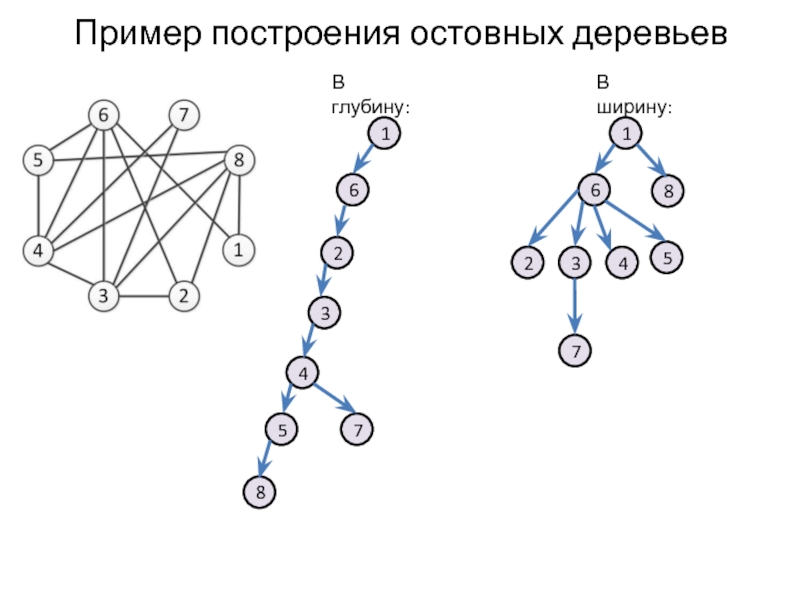
- 21. Пример построения остовных деревьев В глубину: В
Слайд 2Поиск в глубину (Depth-first search, DFS)
Пусть задан граф G = (V,
E).
Алгоритм поиска описывается следующим образом:
для каждой непройденной вершины необходимо найти все непройденные смежные вершины и повторить поиск для них.
Пусть в начальный момент времени все вершины окрашены в белый цвет.
Из множества всех белых вершин выберем любую вершину: v1.
Выполним для нее процедуру Поиск(v1).
Перекрасим ее в черный цвет.
Повторяем шаги 1-3 до тех пор, пока множество белых вершин не пусто.
Алгоритм поиска описывается следующим образом:
для каждой непройденной вершины необходимо найти все непройденные смежные вершины и повторить поиск для них.
Пусть в начальный момент времени все вершины окрашены в белый цвет.
Из множества всех белых вершин выберем любую вершину: v1.
Выполним для нее процедуру Поиск(v1).
Перекрасим ее в черный цвет.
Повторяем шаги 1-3 до тех пор, пока множество белых вершин не пусто.
Слайд 3Процедура Поиск(u)
Поиск (u)
{
цвет [u] ← серый;
d[u] =
time++; // время входа в вершину,
// порядковый глубинный номер вершины
для ∀ v ∈ смежные(u) выполнить
{ если (цвет[v] = белый) то
{
отец [v] ← u;
Поиск(v);
}
}
цвет[u] ← чёрный;
f [u] ← time++; // время выхода из вершины
}
// порядковый глубинный номер вершины
для ∀ v ∈ смежные(u) выполнить
{ если (цвет[v] = белый) то
{
отец [v] ← u;
Поиск(v);
}
}
цвет[u] ← чёрный;
f [u] ← time++; // время выхода из вершины
}
Слайд 4Процедура Поиск_в_графе
Поиск_в_графе()
{
для ∀u ∈ V выполнить
{
цвет [u] ← белый;
отец [u] ← NULL;
}
time ← 0;
для ∀u ∈ V выполнить
если (цвет [u] = белый) то
Поиск(u);
}
}
time ← 0;
для ∀u ∈ V выполнить
если (цвет [u] = белый) то
Поиск(u);
}
Слайд 5Анализ
Общее число операций при выполнении Поиск_в_графе:
O(|V|)
Общее число операций при выполнении Поиск(u):
Цикл
выполняется |смежные[v]| раз.
∑ |смежные[v]| = O(|E|)
Общее число операций: O(|V|+|E|)
∑ |смежные[v]| = O(|E|)
Общее число операций: O(|V|+|E|)
Слайд 7Глубинный остовный лес
Поиск в глубину на неориентированном графе G= (V, Е)
разбивает ребра, составляющие Е, на два множества Т и В.
Ребро (v, w) помещается в множество Т, если узел w не посещался до того момента, когда мы, рассматривая ребро (и, w), оказались в узле v. В противном случае ребро (v, w) помещается в множество В.
Ребра из Т будем называть древесными, а из В — обратными.
Подграф (V, Т) представляет собой неориентированный лес, называемый остовным лесом для G, построенным поиском в глубину, или, короче, глубинным остовным лесом для G.
Если этот лес состоит из единственного дерева, (V, Т) будем называть по аналогии глубинным остовным деревом.
Заметим, что если граф связен, то глубинный остовный лес будет деревом.
Узел, с которого начинался поиск, считается корнем соответствующего дерева.
Ребро (v, w) помещается в множество Т, если узел w не посещался до того момента, когда мы, рассматривая ребро (и, w), оказались в узле v. В противном случае ребро (v, w) помещается в множество В.
Ребра из Т будем называть древесными, а из В — обратными.
Подграф (V, Т) представляет собой неориентированный лес, называемый остовным лесом для G, построенным поиском в глубину, или, короче, глубинным остовным лесом для G.
Если этот лес состоит из единственного дерева, (V, Т) будем называть по аналогии глубинным остовным деревом.
Заметим, что если граф связен, то глубинный остовный лес будет деревом.
Узел, с которого начинался поиск, считается корнем соответствующего дерева.
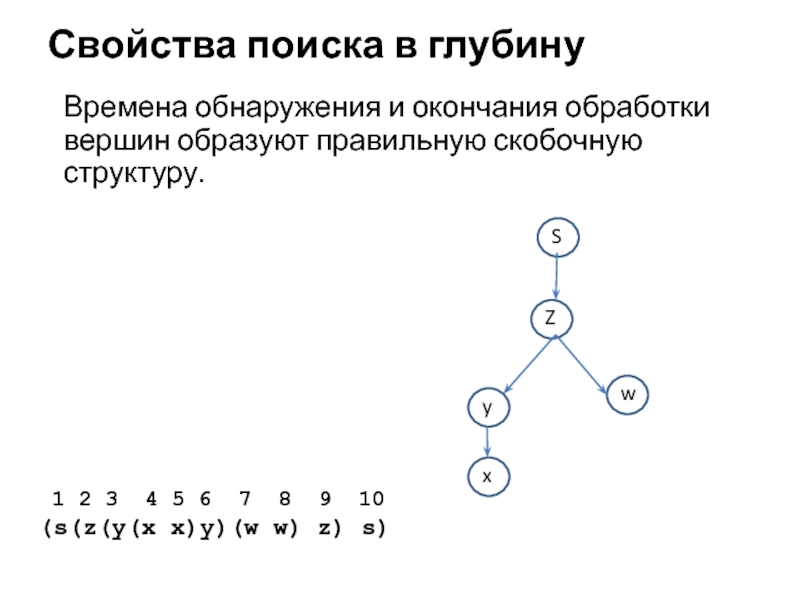
Слайд 8Свойства поиска в глубину
Времена обнаружения и окончания обработки вершин образуют правильную
скобочную структуру.
1 2 3 4 5 6 7 8 9 10 (s(z(y(x x)y)(w w) z) s)
Z
w
S
x
y
Слайд 9Теорема
При поиске в глубину в графе G = (V, E) для
любых двух вершин u и v выполняется одно из следующих утверждений:
Отрезки [d[u],f[u]] и [d[v],f[v]] не пересекаются.
Отрезок [d[u],f[u]] целиком содержится внутри отрезка [d[v],f[v]] и u есть потомок v в дереве поиска в глубину.
Отрезок [d[v],f[v]] целиком содержится внутри отрезка [d[u],f[u]] и v есть потомок u в дереве поиска в глубину.
Отрезки [d[u],f[u]] и [d[v],f[v]] не пересекаются.
Отрезок [d[u],f[u]] целиком содержится внутри отрезка [d[v],f[v]] и u есть потомок v в дереве поиска в глубину.
Отрезок [d[v],f[v]] целиком содержится внутри отрезка [d[u],f[u]] и v есть потомок u в дереве поиска в глубину.
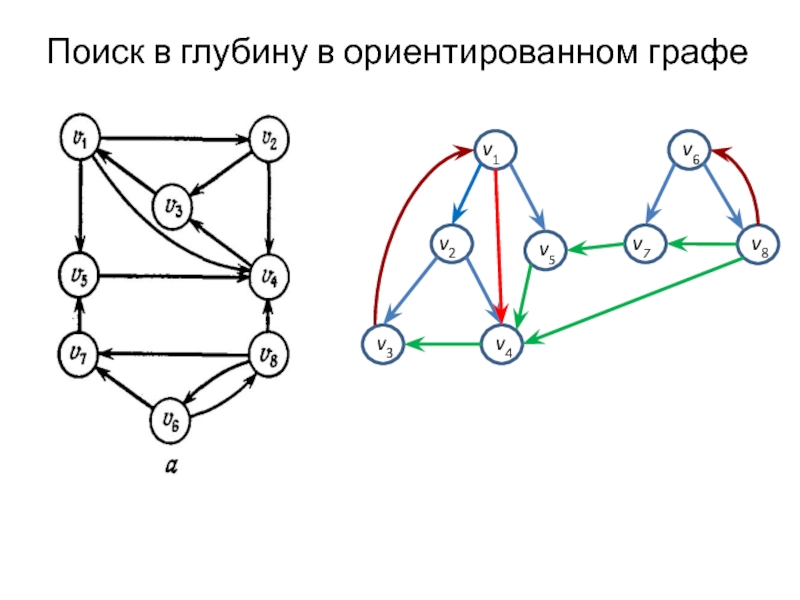
Слайд 11Поиск в глубину в ориентированном графе G разбивает множество его ребер
на четыре класса.
1) Древесные ребра, идущие к новым узлам в процессе поиска.
2) Прямые ребра, идущие от предков к подлинным потомкам, но не являющиеся древесными ребрами.
3) Обратные ребра, идущие от потомков к предкам (возможно, из узла в себя).
4) Поперечные ребра, соединяющие узлы, которые не являются ни предками, ни потомками друг друга.
1) Древесные ребра, идущие к новым узлам в процессе поиска.
2) Прямые ребра, идущие от предков к подлинным потомкам, но не являющиеся древесными ребрами.
3) Обратные ребра, идущие от потомков к предкам (возможно, из узла в себя).
4) Поперечные ребра, соединяющие узлы, которые не являются ни предками, ни потомками друг друга.
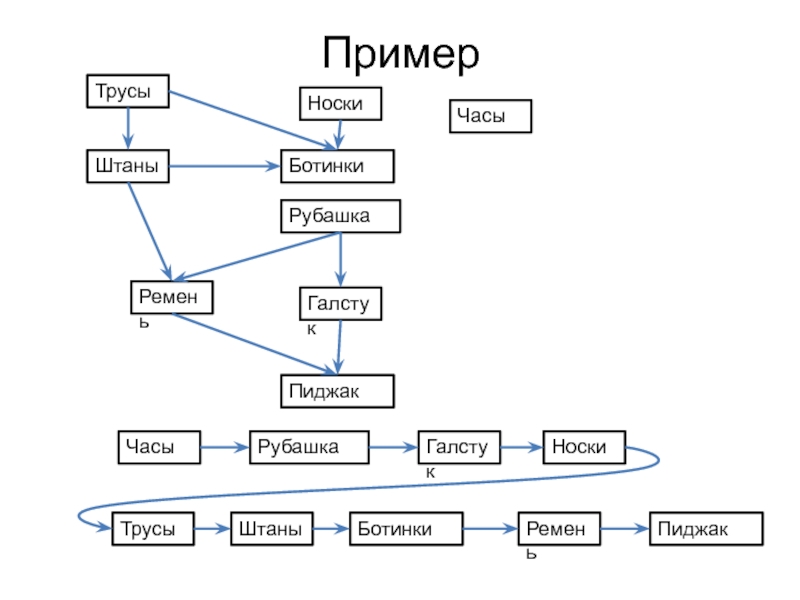
Слайд 12Решение задачи топологической сортировки методом поиска в глубину
Топологическая_сортировка (u)
{
цвет [u]
← серый;
для ∀ v ∈ смежные(u) выполнить
{ если (цвет[v] = белый) то
{
Топологическая_сортировка(v);
}
}
цвет[u] ← чёрный;
Поместить u в начало списка;
}
для ∀ v ∈ смежные(u) выполнить
{ если (цвет[v] = белый) то
{
Топологическая_сортировка(v);
}
}
цвет[u] ← чёрный;
Поместить u в начало списка;
}
Слайд 13Пример
Трусы
Носки
Штаны
Ремень
Ботинки
Рубашка
Галстук
Пиджак
Часы
Пиджак
Ремень
Ботинки
Штаны
Трусы
Носки
Галстук
Рубашка
Часы
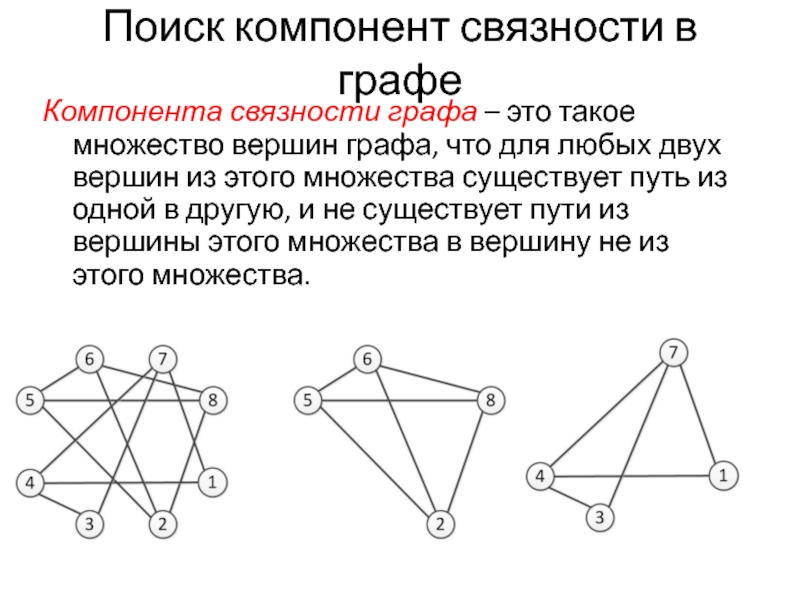
Слайд 14Поиск компонент связности в графе
Компонента связности графа – это такое множество
вершин графа, что для любых двух вершин из этого множества существует путь из одной в другую, и не существует пути из вершины этого множества в вершину не из этого множества.
Слайд 15Реализация поиска компонент связности в графе
Поиск (u, n)
{
цвет [u] ←
серый;
C[u] ← n; // номер компоненты связности
для ∀ v ∈ смежные(u) выполнить
{ если (цвет[v] = белый) то
Поиск(v, n);
}
цвет[u] ← чёрный;
}
Поиск_в_графе()
{
для ∀u ∈ V выполнить
цвет [u] ← белый;
nk ← 0;
для ∀u ∈ V выполнить
если (цвет [u] = белый) то
{
nk ++;
Поиск(u, nk);
}
}
C[u] ← n; // номер компоненты связности
для ∀ v ∈ смежные(u) выполнить
{ если (цвет[v] = белый) то
Поиск(v, n);
}
цвет[u] ← чёрный;
}
Поиск_в_графе()
{
для ∀u ∈ V выполнить
цвет [u] ← белый;
nk ← 0;
для ∀u ∈ V выполнить
если (цвет [u] = белый) то
{
nk ++;
Поиск(u, nk);
}
}
Слайд 16Метод поиска в ширину (BFS, Breadth-first search)
Пусть задан граф G
= (V, E) и некоторая начальная вершина s.
Алгоритм поиска в ширину перечисляет все достижимые из s вершины в порядке возрастания расстояния от s. Расстоянием считается число ребер кратчайшего пути.
Время работы алгоритма - O(|V|+ |E|) .
Пусть в начальный момент времени все вершины окрашены в белый цвет.
Вершину s окрасим в серый цвет и припишем расстояние 0. Смежные с ней вершины окрасим в серый цвет, припишем им расстояние 1, их предок - s. Окрасим вершину s в черный цвет.
На шаге n поочередно рассматриваем белые вершины, смежные с вершинами с пометками n -1, и каждую из них раскрашиваем в серый цвет, приписываем им предка и расстояние n. После этого вершины с расстоянием n-1 окрашиваются в черный цвет.
Алгоритм поиска в ширину перечисляет все достижимые из s вершины в порядке возрастания расстояния от s. Расстоянием считается число ребер кратчайшего пути.
Время работы алгоритма - O(|V|+ |E|) .
Пусть в начальный момент времени все вершины окрашены в белый цвет.
Вершину s окрасим в серый цвет и припишем расстояние 0. Смежные с ней вершины окрасим в серый цвет, припишем им расстояние 1, их предок - s. Окрасим вершину s в черный цвет.
На шаге n поочередно рассматриваем белые вершины, смежные с вершинами с пометками n -1, и каждую из них раскрашиваем в серый цвет, приписываем им предка и расстояние n. После этого вершины с расстоянием n-1 окрашиваются в черный цвет.
Слайд 17Алгоритм
Инициализация
для ( ∀u ∈ (V\{s}) выполнить
{
цвет[u] ← белый;
предок[u]← NULL;
d[u]← ∞;
}
d[s]← 0;
предок[s]← NULL;
put (s, Q);
d[u]← ∞;
}
d[s]← 0;
предок[s]← NULL;
put (s, Q);
Слайд 18пока (Q ≠ ∅) выполнить
{
u ← first (Q);
для ( ∀v ∈
смежные[u])выполнить
{ если (цвет[v]= белый) то
{
цвет [v] ← серый;
предок[v]← u;
d[v]← d[u]+1;
put(v,Q);
}
}
get(Q);
цвет[u] ← черный;
}
{ если (цвет[v]= белый) то
{
цвет [v] ← серый;
предок[v]← u;
d[v]← d[u]+1;
put(v,Q);
}
}
get(Q);
цвет[u] ← черный;
}
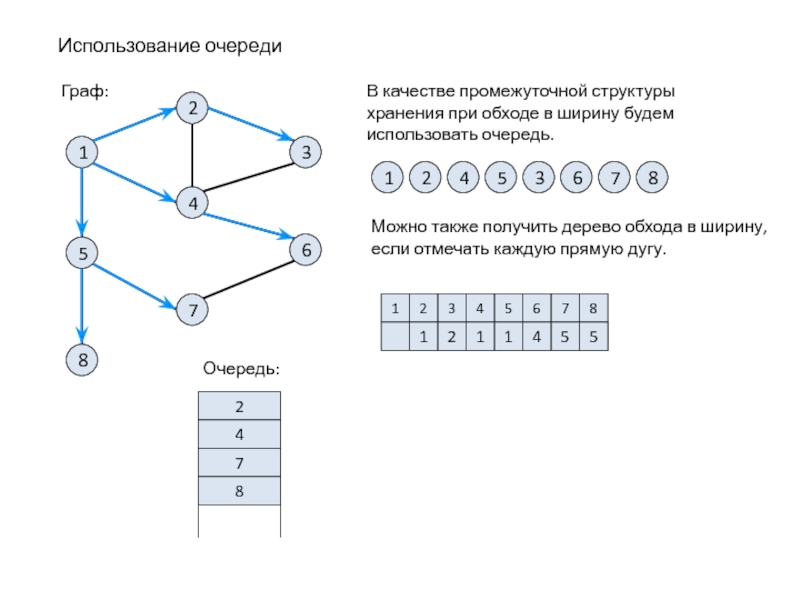
Слайд 19Использование очереди
В качестве промежуточной структуры
хранения при обходе в ширину будем
использовать очередь.
1
2
3
4
6
7
5
8
Граф:
1
Можно также получить дерево обхода в ширину,
если отмечать каждую прямую дугу.
1
1
2
1
1
4
5
5
2
3
4
5
6
7
8
4
2
3
5
7
6
8
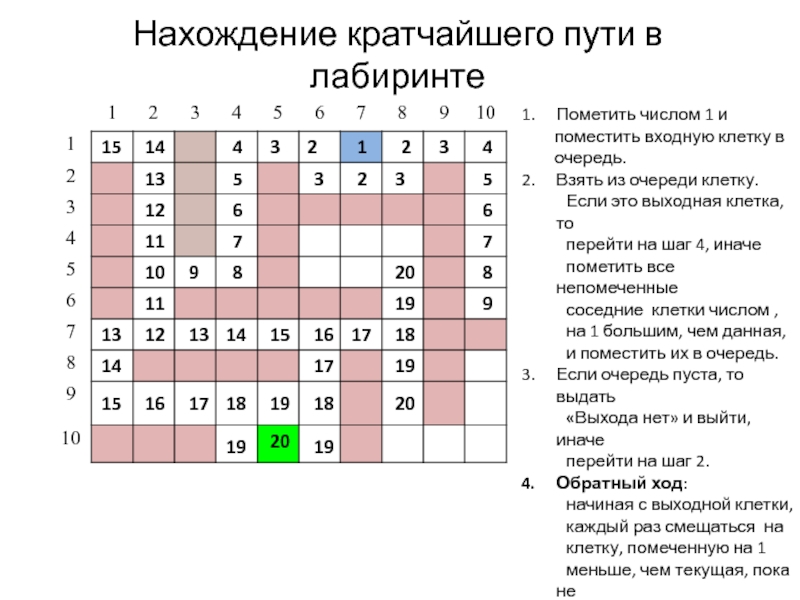
Слайд 20Нахождение кратчайшего пути в лабиринте
1
2
2
3
2
3
3
3
4
4
5
5
6
6
7
7
8
8
9
9
10
11
11
12
12
13
13
13
14
14
14
15
15
15
16
16
17
17
17
18
18
18
19
19
19
19
19
20
20
20
Пометить числом 1 и
поместить входную клетку в
очередь.
Взять из очереди клетку.
Если это выходная клетка, то
перейти на шаг 4, иначе
пометить все непомеченные
соседние клетки числом ,
на 1 большим, чем данная,
и поместить их в очередь.
Если очередь пуста, то выдать
«Выхода нет» и выйти, иначе
перейти на шаг 2.
Обратный ход:
начиная с выходной клетки,
каждый раз смещаться на
клетку, помеченную на 1
меньше, чем текущая, пока не
дойдем до входной клетки.
При проходе выделять
пройденные клетки.
очередь.
Взять из очереди клетку.
Если это выходная клетка, то
перейти на шаг 4, иначе
пометить все непомеченные
соседние клетки числом ,
на 1 большим, чем данная,
и поместить их в очередь.
Если очередь пуста, то выдать
«Выхода нет» и выйти, иначе
перейти на шаг 2.
Обратный ход:
начиная с выходной клетки,
каждый раз смещаться на
клетку, помеченную на 1
меньше, чем текущая, пока не
дойдем до входной клетки.
При проходе выделять
пройденные клетки.


![Процедура Поиск(u)Поиск (u){ цвет [u] ← серый; d[u] = time++; // время входа в](/img/tmb/3/266852/9a8a738c4cf4330fbb90fdb97fbcab14-800x.jpg)
![Процедура Поиск_в_графеПоиск_в_графе(){ для ∀u ∈ V выполнить { цвет [u] ← белый; отец [u] ← NULL; }](/img/tmb/3/266852/bf099c2595185c8343966a36a8321e03-800x.jpg)
![АнализОбщее число операций при выполнении Поиск_в_графе: O(|V|)Общее число операций при выполнении Поиск(u):Цикл выполняется |смежные[v]| раз. ∑ |смежные[v]|](/img/tmb/3/266852/f5616e942128bc05f2697f9861986f53-800x.jpg)



![Решение задачи топологической сортировки методом поиска в глубинуТопологическая_сортировка (u){ цвет [u] ← серый; для](/img/tmb/3/266852/676bfea4b9f5068175e26d244cca6d87-800x.jpg)
![Реализация поиска компонент связности в графеПоиск (u, n){ цвет [u] ← серый; C[u] ← n;](/img/tmb/3/266852/7b3e0b5acc8bdafbe39b8b72a950c152-800x.jpg)

![Алгоритм Инициализациядля ( ∀u ∈ (V\{s}) выполнить{ цвет[u] ← белый; предок[u]← NULL; d[u]← ∞; }d[s]←](/img/tmb/3/266852/9a7d6370753a79ffd6018407da05c3d1-800x.jpg)
![пока (Q ≠ ∅) выполнить{ u ← first (Q); для ( ∀v ∈ смежные[u])выполнить { если](/img/tmb/3/266852/4171caa344d08fed561e3f63edac3927-800x.jpg)