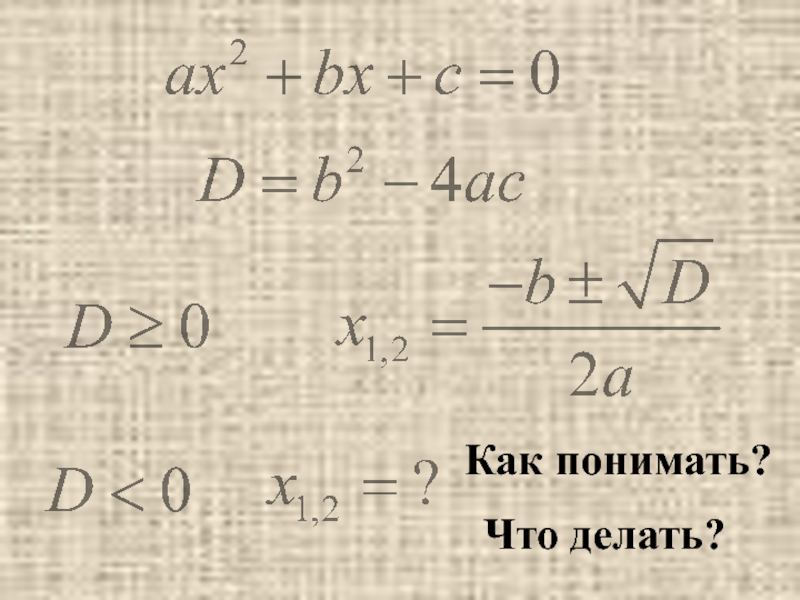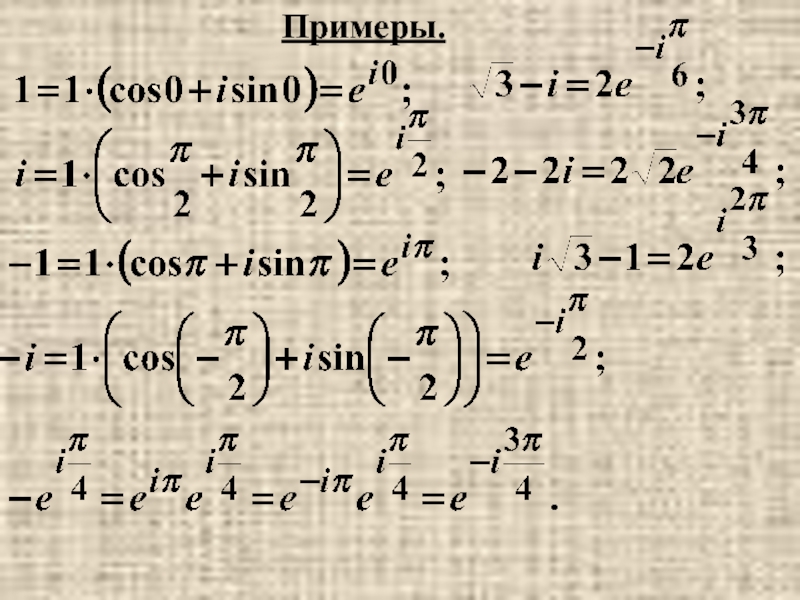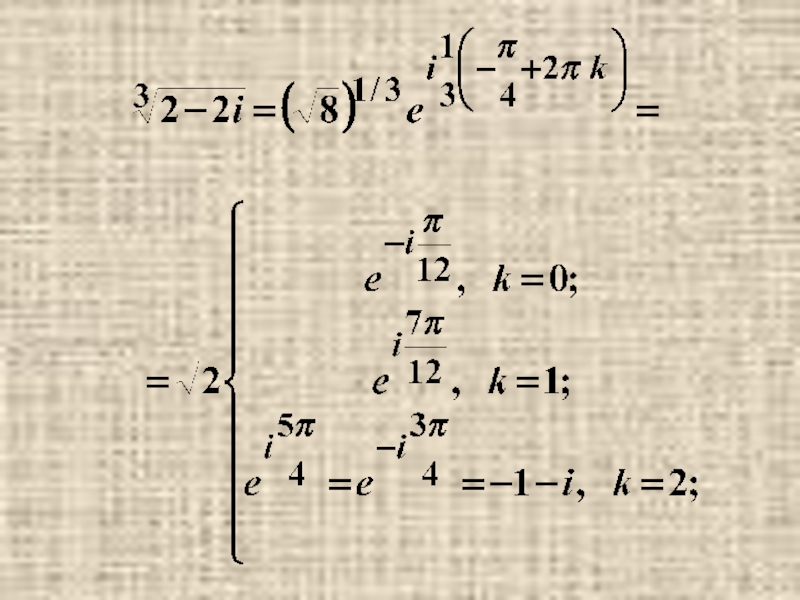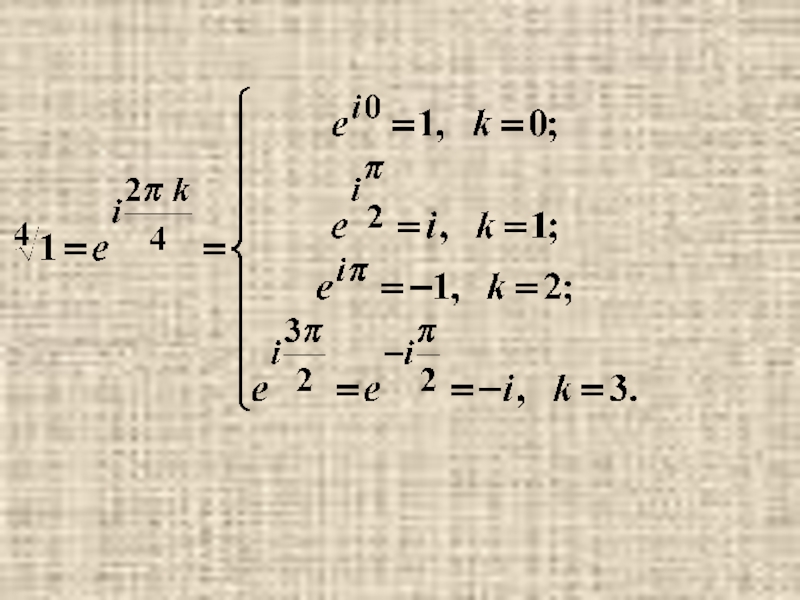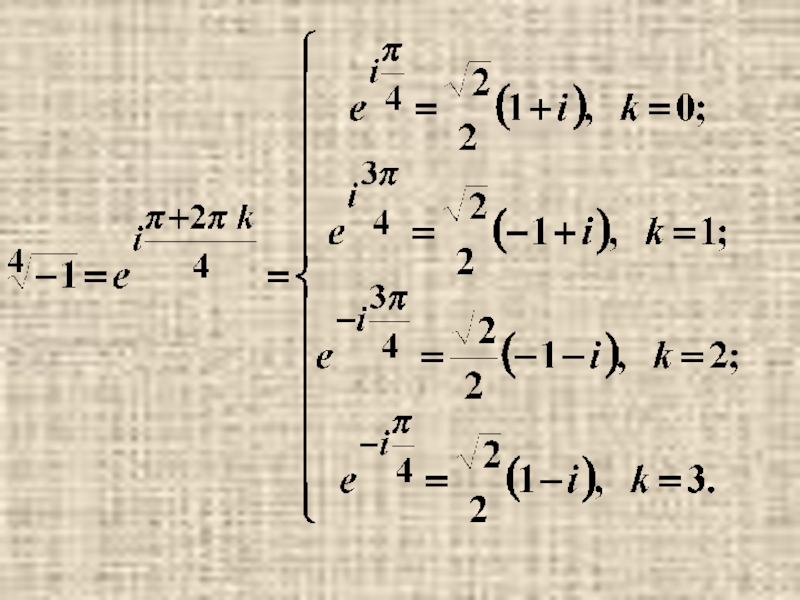функции комплексной переменной
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекции по теории функции комплексной переменной презентация
Содержание
- 1. Лекции по теории функции комплексной переменной
- 2. Лекция № 1 §1. Комплексные числа и
- 3. Немного истории Комплексные числа вошли в
- 4. Как понимать? Что делать?
- 5. Вначале такие корни отбрасывались, как «невозможные», «мнимые»,
- 6. Обоснование: мнимые корни не выражают величины, так
- 7. Однако позже было обнаружено, что над ними
- 8. Это и послужило основанием называть мнимые корни
- 9. Геометрическое изображение комплексных чисел в виде точек
- 10. Символ i для мнимой единицы ввел в
- 11. Большое значение в раскрытии важной роли комплексных
- 12. До появления этой теоремы можно было бы
- 13. Геометрическое изображение комплексного числа как точки или
- 14. Однако поиски числовой системы, зависящей от трех
- 15. В 1843 т. английский математик У.
- 16. Вообще, гиперкомплексными числами ранга п называются «числа»
- 17. Однако К. Вейерштрасс показал, что при п
- 18. Немецкий математик Ф. Фробениус (1849—1917) доказал, что,
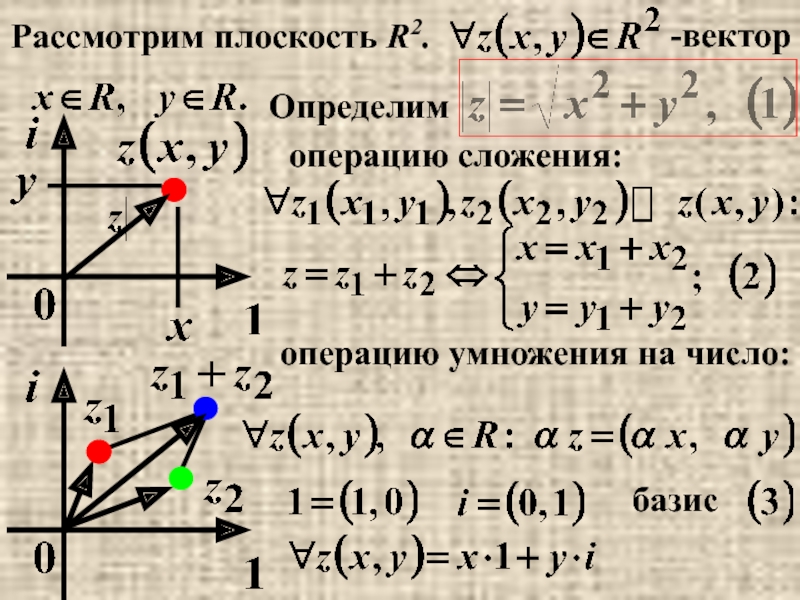
- 19. -вектор Определим операцию сложения: операцию умножения на число: базис Рассмотрим плоскость R2.
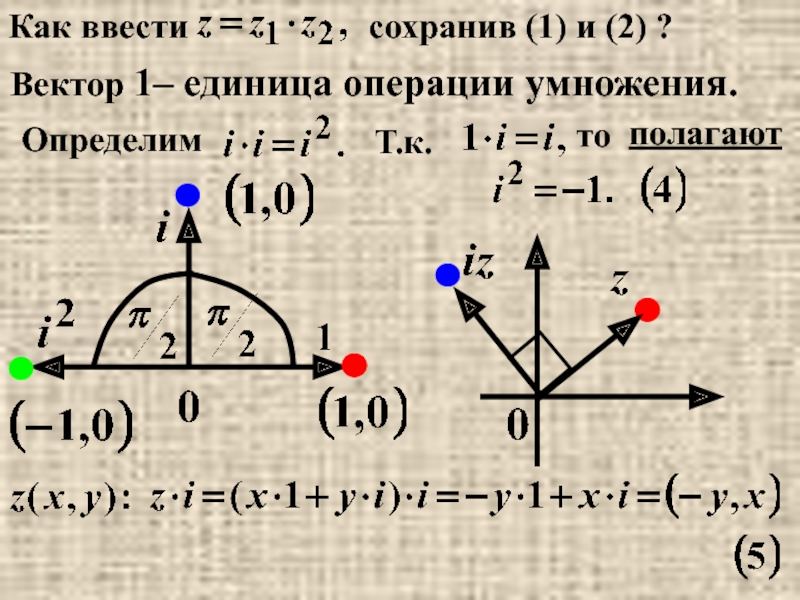
- 20. Как ввести сохранив (1) и (2) ?
- 21. Правило умножения Def. Числовая плоскость называется
- 22. Действительные числа включаются в множество комплексных чисел.
- 23. Деление. Комплексное сопряжение.
- 24. Примеры.
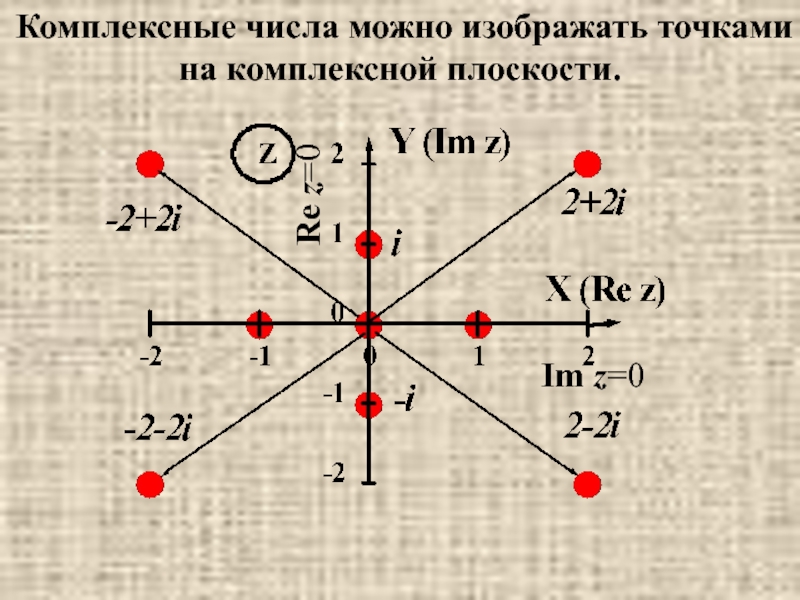
- 25. Комплексные числа можно изображать точками на комплексной плоскости. Im z=0 Re z=0
- 27. Модуль и аргумент комплексного числа Полярные координаты
- 28. -разрез по - PC Soft -разрез по -литература Примеры. — не определен!
- 29. Тригонометрическая форма записи формула Эйлера: Показательная форма записи Теорема. Пусть тогда
- 30. Примеры.
- 31. Вопрос. Умножение и деление в показательной форме. Формула Муавра.
- 32. Извлечение корня. Корень n-той степени из комплексного числа принимает n различных значений.
- 33. Примеры.
- 37. Операция сравнения в С не определена.
- 38. Неравенства треугольника. Упорядоченная четверка является нормированным векторным
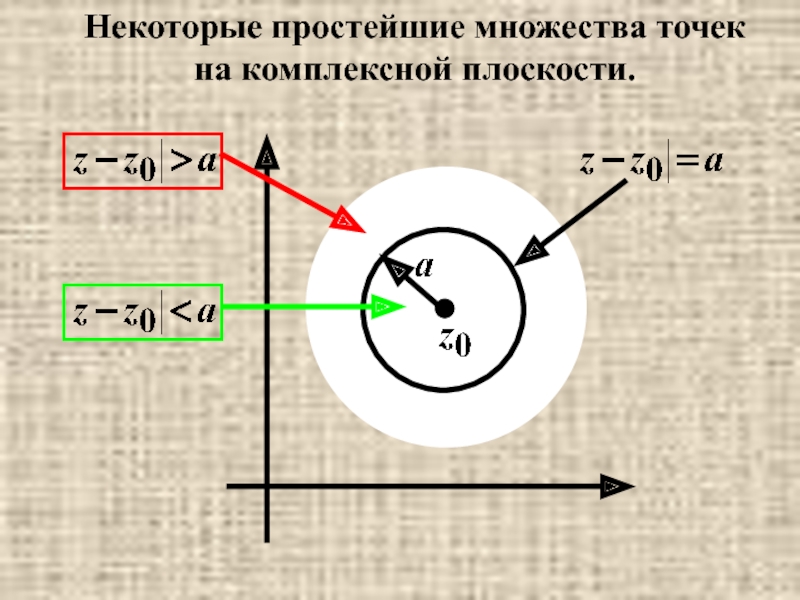
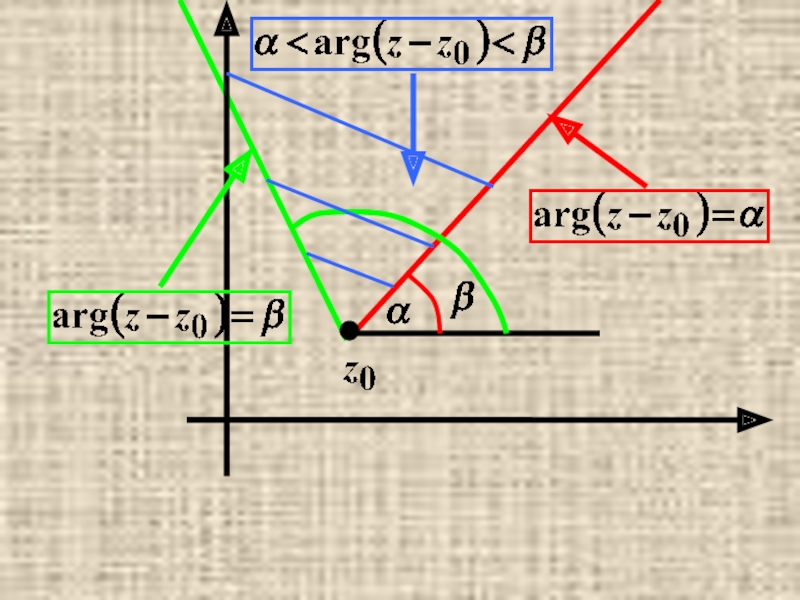
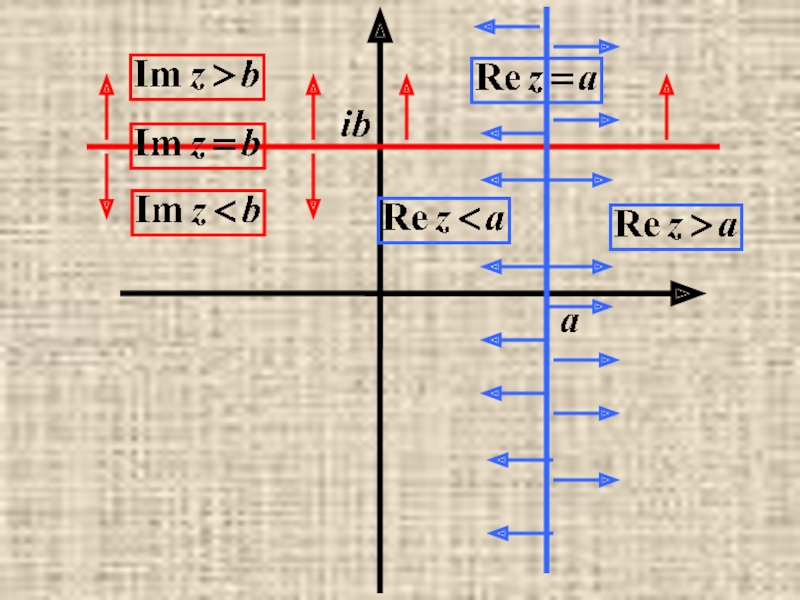
- 39. Некоторые простейшие множества точек на комплексной плоскости.
Лекция № 1 §1. Комплексные числа и последовательности комплексных чисел. п. 1. Понятие комплексного числа. Геометрическая интерпретация.
Слайд 1Московский государственный университет
им. М.В. Ломоносова
Физический факультет
Кафедра математики
Виктор Юрьевич Попов
Лекции по теории
Слайд 2Лекция № 1
§1. Комплексные числа и
последовательности комплексных
чисел.
п. 1. Понятие
комплексного числа.
Геометрическая интерпретация.
Геометрическая интерпретация.
Слайд 3Немного истории
Комплексные числа вошли в математику в XVI в. как
корни квадратного уравнения с отрицательным дискриминантом.
Слайд 5Вначале такие корни отбрасывались, как «невозможные», «мнимые», и появление их считалось
признаком отсутствия решения у задачи, приведшей к квадратному уравнению.
Слайд 6Обоснование: мнимые корни не выражают величины, так как их нельзя сравнивать
друг с другом, нельзя сказать, какоe мнимое больше, какое меньше.
Слайд 7Однако позже было обнаружено, что над ними можно производить четыре алгебраических
действия, причем сохраняются свойства, присущие действиям над действительными числами.
Слайд 8Это и послужило основанием называть мнимые корни числами
(«Алгебра» итальянского инженера
Р. Бомбелли, 1572 г.).
Слайд 9Геометрическое изображение комплексных чисел в виде точек или векторов "на плоскости"
было введено в 1799 г. датским землемером
К. Весселем (1745—1818)
и несколько позже, в 1806 г., французским математиком
Д. Арганом (1768—1822).
К. Весселем (1745—1818)
и несколько позже, в 1806 г., французским математиком
Д. Арганом (1768—1822).
Слайд 10Символ i для мнимой единицы ввел в 1777 г. Л. Эйлер
(1707— 1783).
Термин «комплексное число» ввел в 1881 г. К. Вейерштрасс (1815— 1897).
Слайд 11Большое значение в раскрытии важной роли комплексных чисел в математике имели
работы Л. Эйлера и К. Гаусса (1777—1855), а также теорема Даламбера (1717—1783) о том, что любое алгебраическое уравнение n-й степени с комплексными коэффициентами имеет n комплексных корней.
Слайд 12До появления этой теоремы можно было бы ожидать, что, подобно тому
как квадратное уравнение привело к комплексным числам, попытки решения уравнений степеней п = 3, 4, ..., приведут к появлению все новых и новых типов чисел.
Слайд 13Геометрическое изображение комплексного числа как точки или вектора на плоскости, естественно,
приводит к мысли построить дальнейшие обобщения понятия о числе.
Слайд 14Однако поиски числовой системы, зависящей от трех единиц: 1, i, j,
геометрически изображаемой с помощью точек или векторов 3-мерного пространства, не увенчались успехом: не удавалось так придумать правила действий над новыми «числами», чтобы сохранились обычные их свойства.
Слайд 15В 1843 т. английский математик
У. Гамильтон (1805—1865) показал, что можно
построить числовые системы, зависящие от четырех единиц: 1, i, j, k, если поступиться одним свойством — переместительным законом умножения.
Слайд 16Вообще, гиперкомплексными числами ранга п называются «числа» вида
— единицы,
—действительные числа,
когда указаны правила алгебраических действий с такими «числами».
Слайд 17Однако К. Вейерштрасс показал, что при п > 2 нельзя сохранить
все свойства, присущие алгебраическим действиям над действительными и комплексными числами.
Слайд 18Немецкий математик Ф. Фробениус (1849—1917) доказал, что, даже отказавшись от переместительного
закона умножения, можно сохранить остальные свойства алгебраических действий дополнительно лишь для п = 4,
а при ,
как бы не вводилось правило умножения, всегда будут пары отличных от нуля гиперкомплексных чисел, произведение которых равно нулю.
а при ,
как бы не вводилось правило умножения, всегда будут пары отличных от нуля гиперкомплексных чисел, произведение которых равно нулю.
Слайд 21Правило умножения
Def. Числовая плоскость
называется
комплексной плоскостью C, если для ее точек
определены
модули (1), операции сложения (2)
и умножения (6).
и умножения (6).
Точки комплексной плоскости С называются
комплексными числами.
Слайд 22Действительные числа включаются в множество комплексных чисел.
a=(a,0)-вещественное число,
-1=(-1, 0),
i =(0, 1)- мнимая единица,
ib= (0, b)-чисто мнимое число,
0=(0, 0),
1=(1, 0),
-i=(0, -1).
упорядоченная пара вещественных чисел.
Равенство.
Алгебраическая форма записи.
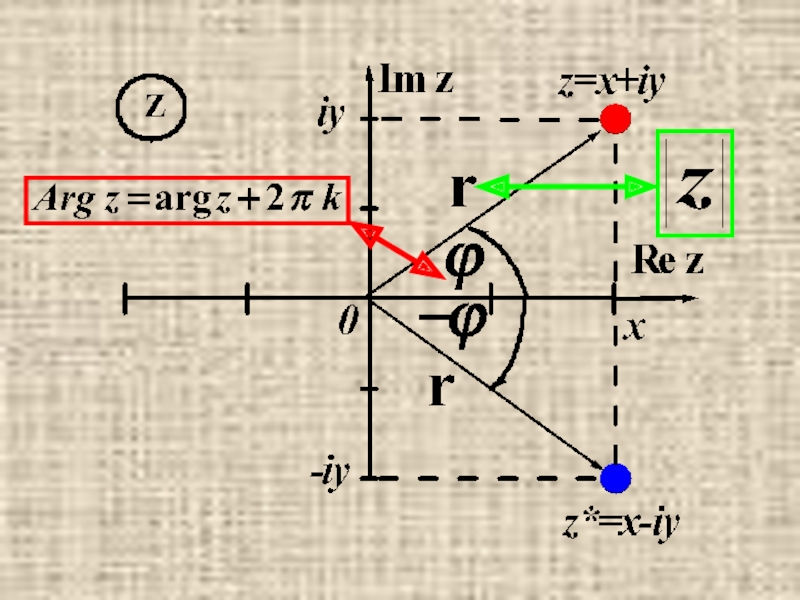
Слайд 27Модуль и аргумент комплексного числа
Полярные координаты
(x,y)↔(r,ϕ).
Модуль комплексного числа:
Аргумент комплексного числа:
Главное значение аргумента.
Слайд 29Тригонометрическая форма записи
формула Эйлера:
Показательная форма записи
Теорема. Пусть
тогда
Слайд 37Операция сравнения в С не определена.
Множество комплексных чисел C образует
поле.
Поле С не является упорядоченным.
В упорядоченном поле P
В поле С
но
Утверждение
неверно.
Модуль
удовлетворяет
аксиомам норм.
Слайд 38Неравенства треугольника.
Упорядоченная четверка
является нормированным векторным
пространством над полем R. Оно превратится
в
метрическое пространство, если
ввести метрику по формуле
Из теоремы Фробениуса следует, что поле С
является «максимальным» числовым полем
и дальнейшее расширение понятия числа
невозможно.
