Матрицы и СЛАУ МНК. (Лекция 5 ) презентация

индекса ( первый - по строке и второй - по столбцу). 

Частные случаи

- единичная матрица – это матрица у которой на главной диагонали 1, а вне главной диагонали 0.

меняются местами строки и столбцы. Транспонированная матрица обозначается верхним индексом «T». Если у исходной матрицы размер (m×n), то у транспонированной матрицы размер (n×m) .

СЛОЖЕНИЕ - матрицы складываются поэлементно (складываем числа на одинаковых местах). !!! Складывать можно только матрицы, имеющие одинаковый размер (т.е. одинаковое число строк и столбцов).

ТРАНСП(массив)

матрицы A равно числу строк матрицы B. Если матрица A имеет размер (m×k), а матрица B имеет размер (k×n), то матрица имеет размер (m×n). При этом AB≠BA.

МУМНОЖ(массив1; массив2)

Пример:

элемент равен произведению соответствующего элемента матрицы А на число k:

Для суммы и произведения матриц справедливы следующие соотношения:

меняет матрицу.

Определитель матрицы – это число, характеризующее матрицу. Если определитель матрицы не равен 0, то говорят, что матрица невырожденная. В противном случае матрицу называют вырожденной.
!!!Определитель вычисляется только для квадратных матриц. 

МОПРЕД(массив)

МОБР(массив)

и для определителя третьего порядка:

+

–

С 3-Я НЕИЗВЕСТНЫМИ

Тройка чисел

называется решением системы (1), если в результате

все три уравнения (1) обращаются в тождества.

подстановки этих чисел вместо

В методе Крамера основную роль будут играть следующие четыре определителя:

– главный определитель системы (1)

Существует несколько методов решения СЛАУ: метод Крамера, Матричный метод ( метод обратной матрицы), метод Гаусса.

В Excel мы будем рассматривать первые два метода.

Метод Крамера

(1) существует и единственно.

– решение единственное

Используя свойства определителей, решение системы (1) можно записать в виде:

– формулы Крамера

Матричная запись системы линейных алгебраических уравнений

– матричная запись СЛАУ

– решение СЛАУ (3) в матричном виде

МОБР(массив)

МУМНОЖ(мас 1; мас 2)

МОПРЕД(массив)

для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки.
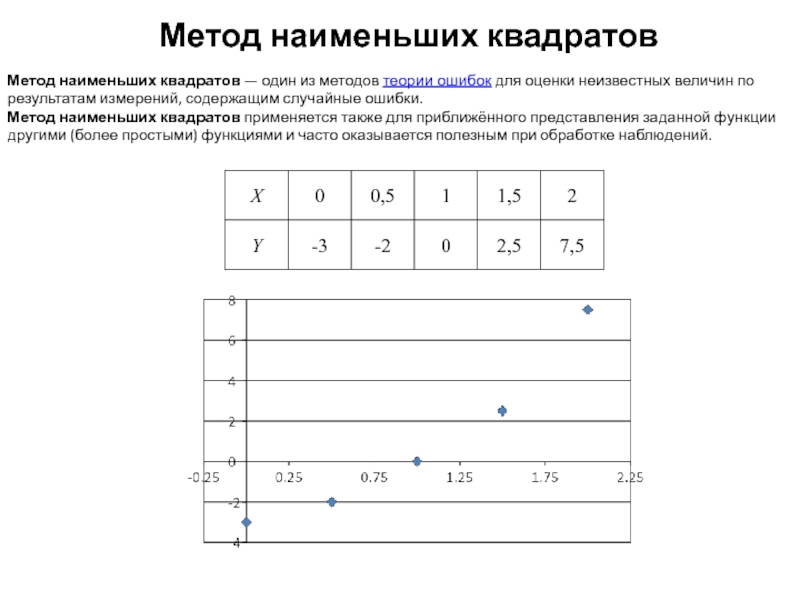
Метод наименьших квадратов применяется также для приближённого представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений.

– координаты заданных точек (данные из таблицы)

– количество заданных точек