- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Matlab. Математические вычисления презентация
Содержание
- 1. Matlab. Математические вычисления
- 2. Содержание Введение Основы Основы Matlab Вычисления в
- 3. Matlab (MATrix LABoratory) – это математические вычисления
- 4. Пакеты, встроенные в Matlab Matlab Web Server
- 5. ОСНОВНЫЕ ЧАСТИ ПАКЕТА MATLAB: Язык Matlab Среда
- 6. Язык Matlab Си- и Паскаль-подобный объектно-ориентированный Огромный
- 7. Среда Matlab Интерактивная работа Управление переменными в рабочем пространстве Редактор Отладчик Содержание Выход
- 8. Управляемая графика Команды высокого уровня для работы
- 9. Библиотека математических функций Обширная коллекция вычислительных
- 10. Программный интерфейс API для взаимодействия с программами
- 11. Matlab – язык для работы с матричными
- 12. Числа Основной базовый тип для матриц Хранятся
- 13. Другие типы Строки Массивы структур (записей) Массивы
- 14. Переменные и выражения Переменные определяются пользователем при
- 15. Содержание Выход
- 16. Операторы При составлении выражений могут быть использованы
- 17. Операции отношения Содержание Выход
- 18. Логические операции Содержание Выход
- 19. Командная строка Простейший способ взаимодействия с Matlab
- 20. Работа с КС упрощается благодаря окну Command
- 21. Рабочее пространство (Workspace) Все переменные хранятся в
- 22. Более подробную информацию о переменных РП можно вывести командой whos: Содержание Выход
- 23. После закрытия сеанса работы MATLABа все переменные,
- 24. Команда save save – сохраняет все переменные
- 25. Команда load Служит для загрузки ранее сохранённых
- 26. Команда clear Служит для удаления переменных из
- 27. Рабочий каталог Все файлы (данные, функции и
- 28. Сохранение рабочей сессии diary – сохраняет лог
- 29. ВЫЧИСЛЕНИЯ В MATLAB Содержание Выход
- 30. Элементарные функции Тригонометрические sin cos tan
- 31. Элементарные функции Экспоненциальные exp log –
- 32. Элементарные функции Округление и остатки fix –
- 33. Элементарные функции Комплексные числа abs(z) – модуль
- 34. Элементарные функции Просмотреть полный список элементарных функций можно командой help elfun Содержание Выход
- 35. Константы pi – число pi Inf –
- 36. Одномерные массивы Задание массива: a = [
- 37. Двумерные массивы Задание массива: a = [
- 38. Векторы-столбцы и векторы-строки Любая строка и столбец
- 39. Размерность и размер матриц Размерность массива определяется
- 40. Конкатенация Рассмотрим две матрицы Проведём склейку «в
- 41. Диапазоны Можно использовать как для задания значений
- 42. Содержание Выход
- 43. Для обращения к последнему элементу любой размерности
- 44. Удаление строк и столбцов Содержание Выход
- 45. Перестановка элементов Содержание Выход
- 46. ФУНКЦИИ ДЛЯ РАБОТЫ С МАССИВАМИ В MATLAB Содержание Выход
- 47. Создание матриц специального вида Для работы с
- 48. МАТРИЦЫ СПЕЦИАЛЬНОГО ВИДА Рассмотрим основной синтаксис на
- 49. Содержание Выход
- 50. Содержание Выход
- 51. Содержание Выход
- 52. Содержание Выход
- 53. Функция diag: работа с диагональными матрицами у
- 54. Содержание Выход
- 55. Содержание Выход
- 56. ВЫЧИСЛЕНИЯ С ЭЛЕМЕНТАМИ МАССИВОВ Простейшие операции над
- 57. Рассмотрим работу некоторых из этих функций на
- 58. Содержание Выход
- 59. Кумулятивная сумма вычисляется так же, только происходит
- 60. Максимальный и минимальный элементы: Содержание Выход
- 61. Вызов функций max/min с двумя выходными параметрами
- 62. Функция sort производит сортировку элементов матрицы по столбцам: Содержание Выход
- 63. ЛОГИЧЕСКИЕ ФУНКЦИИ All(v) – возвращает истину, если
- 64. Any(v) – возвращает истину, если хотя бы
- 65. Содержание Выход
- 66. Поиск в массиве find: определяет индексы элементов, удовлетворяющих заданному условию Содержание Выход
- 67. Пример применения команды find к матрицам: Содержание Выход
- 68. Математические матричные операции det – вычисление определителя квадратной матрицы Содержание Выход
- 69. МАТРИЧНЫЕ И ПОЭЛЕМЕНТНЫЕ ОПЕРАЦИИ При работе с
- 70. ‘ транспонирование + матричное (и поэлементное)
- 71. Содержание Выход
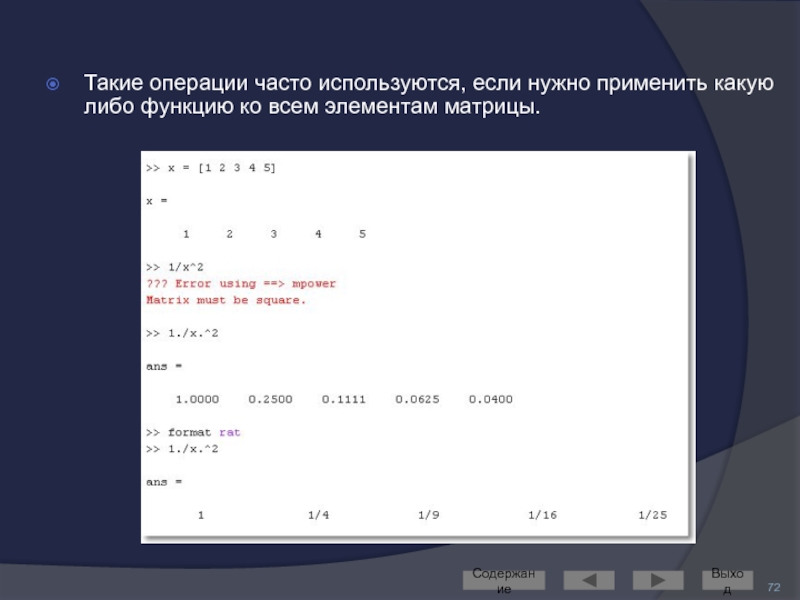
- 72. Такие операции часто используются, если нужно применить
- 73. Некоторые операции по умолчанию считаются поэлементными: Содержание Выход
- 74. Операции «деления» слева и справа Применяются для
- 75. ГРАФИЧЕСКИЕ ВОЗМОЖНОСТИ MATLAB Содержание Выход
- 76. Графика в Matlab Высокоуровневая не требует
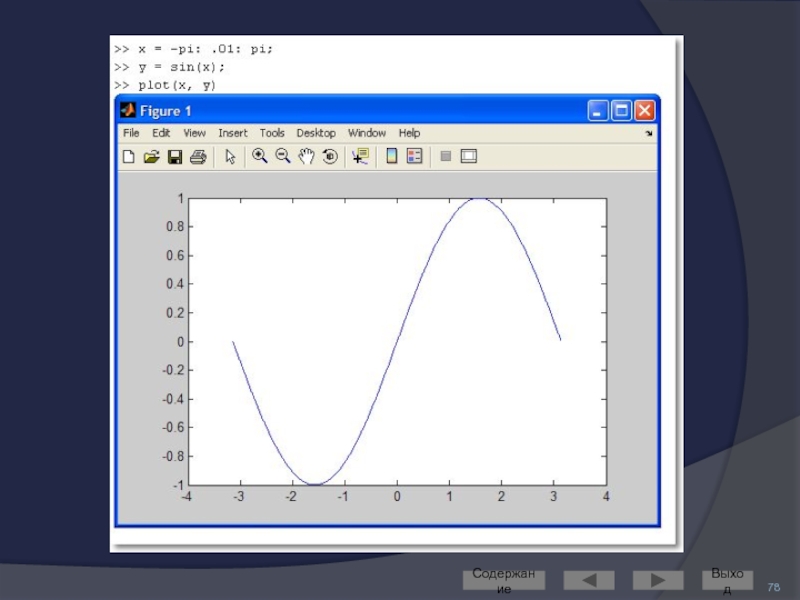
- 77. Двумерные (2D-) графики Простейший способ построения 2D-графика:
- 78. Содержание Выход
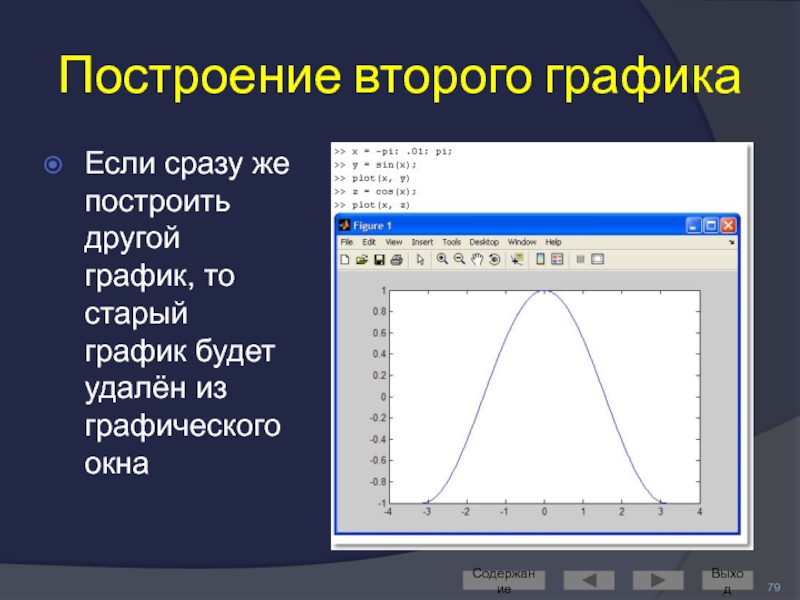
- 79. Построение второго графика Если сразу же построить
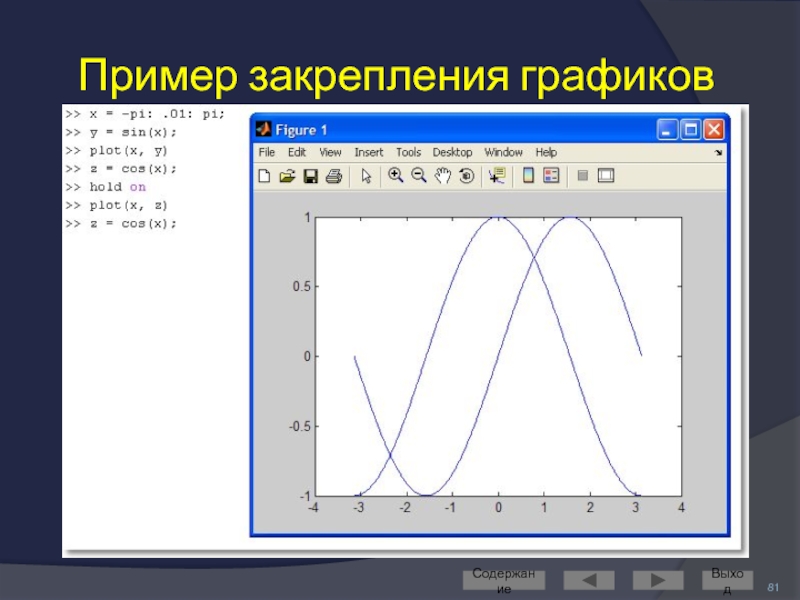
- 80. Построение двух графиков в одной системе координат
- 81. Пример закрепления графиков Содержание Выход
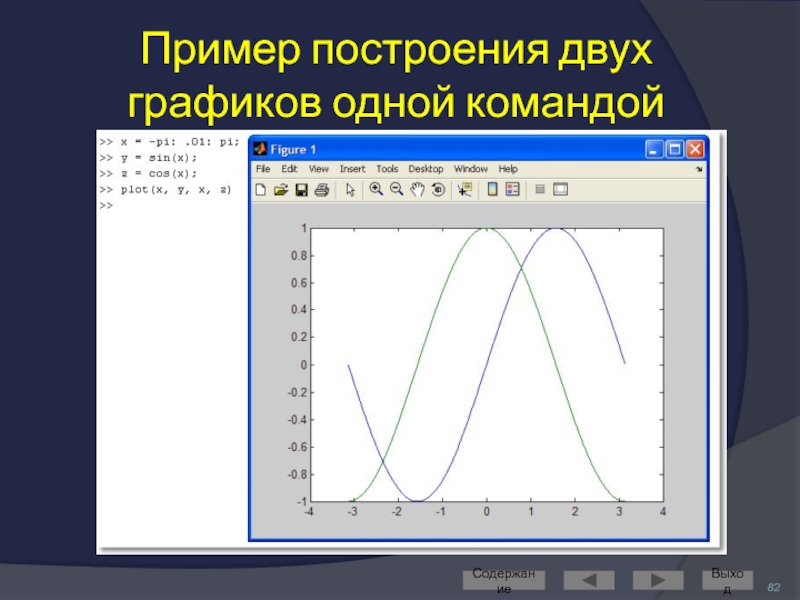
- 82. Содержание Выход Пример построения двух графиков одной командой
- 83. В команде plot можно задать для каждого
- 84. Пример команды plot Содержание Выход
- 85. Построение нескольких графиков в одном окне в
- 86. Первый subplot Содержание Выход
- 87. Второй subplot Содержание Выход
- 88. Содержание Выход
- 89. Построение графиков в разных графических окнах Создать
- 90. figure : пример использования 1 Содержание Выход
- 91. Содержание Выход figure : пример использования 2
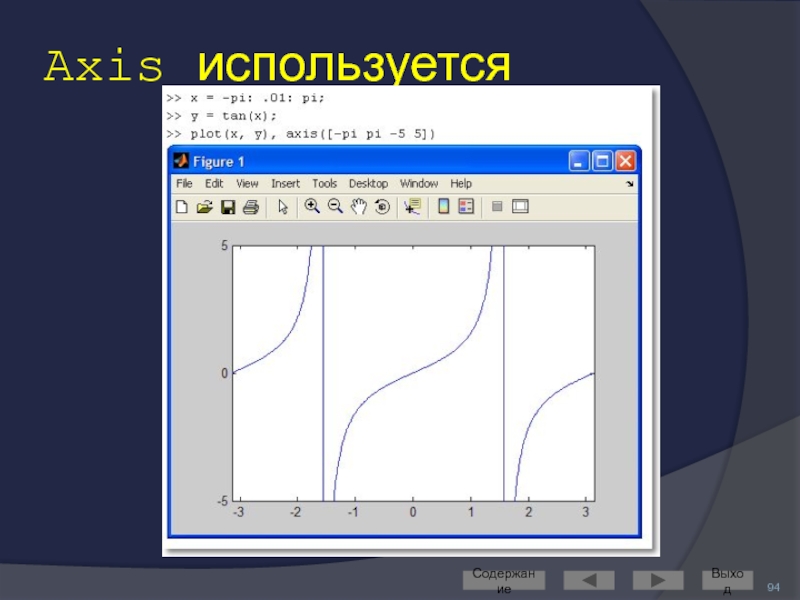
- 92. Axis: управление масштабом Команда axis([Xmin Xmax
- 93. Axis не используется Содержание Выход
- 94. Axis используется Содержание Выход
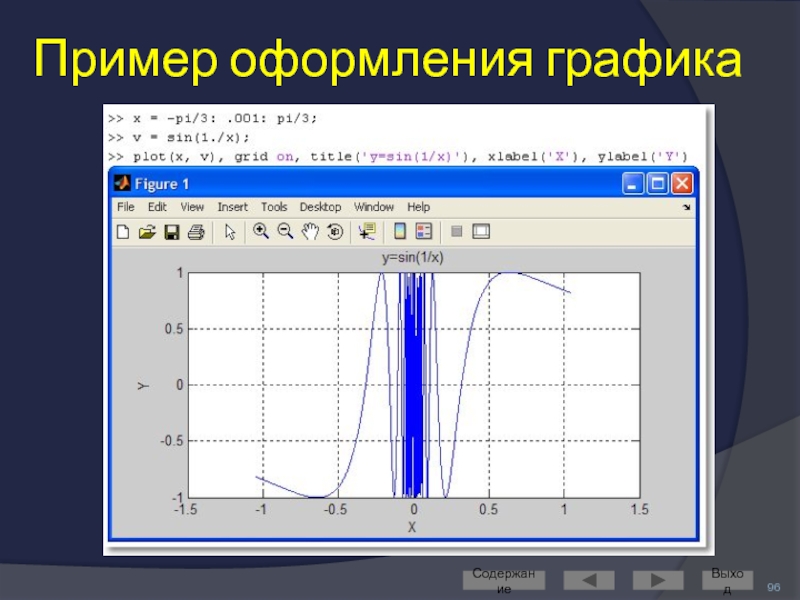
- 95. Оформление графиков Для графиков можно задать масштабную
- 96. Пример оформления графика Содержание Выход
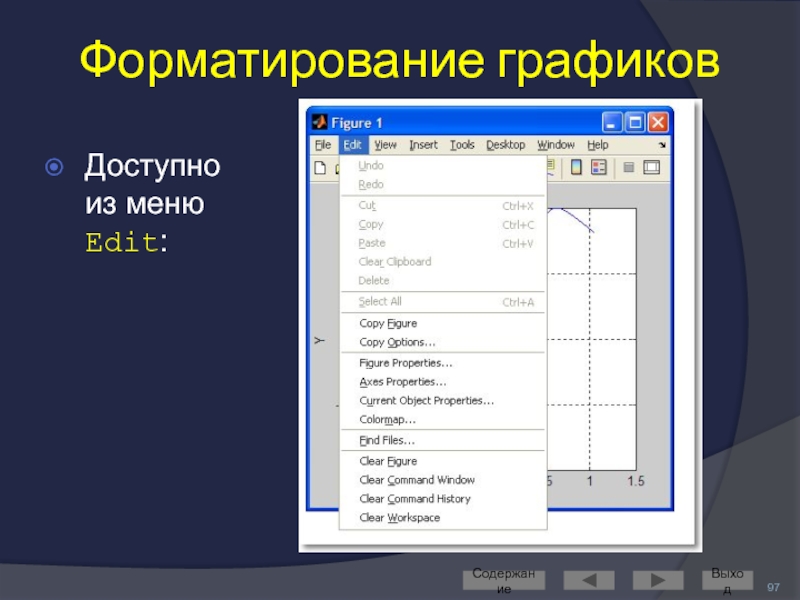
- 97. Форматирование графиков Доступно из меню Edit: Содержание Выход
- 98. Графики функций, заданных параметрически Строятся при помощи
- 99. Содержание Выход
- 100. Графики параметрических функций часто возникают в физических
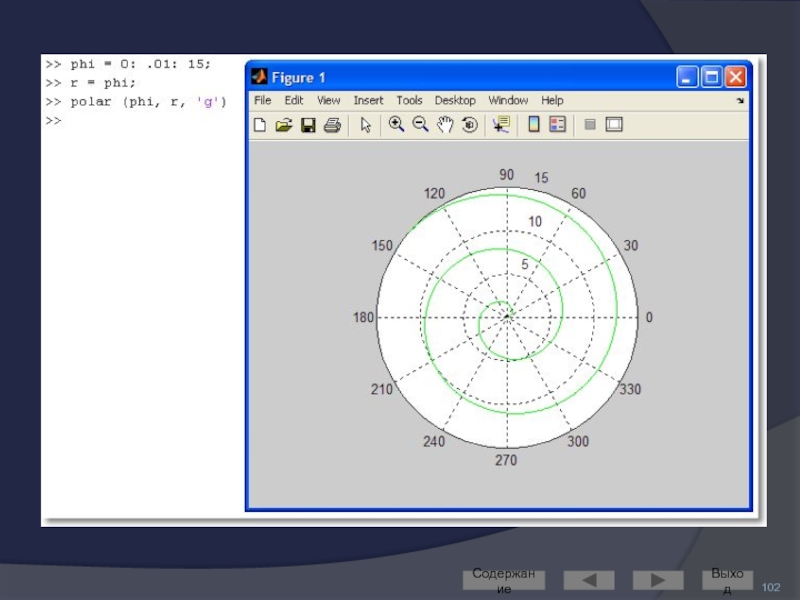
- 101. Функции в полярной СК Строятся аналогично графикам
- 102. Содержание Выход
- 103. Построение поверхностей контурных диаграмм (линии равного
- 104. Содержание Выход
- 105. Построение 3D-поверхности Рассмотрим пример: построить поверхность f(x,y)=sin(r)/r, где r=sqrt(x2+y2) Содержание Выход
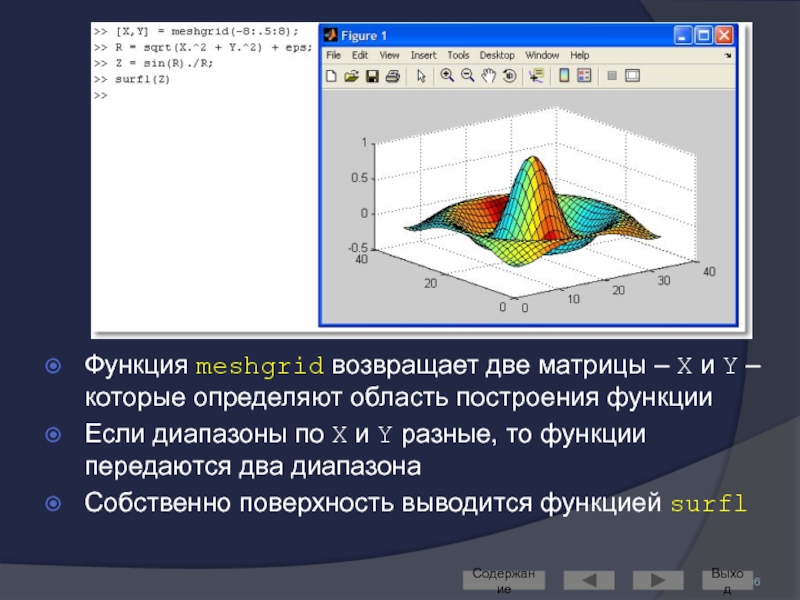
- 106. Функция meshgrid возвращает две матрицы – X
- 107. Функции для построения поверхностей О других графических
- 108. ПРОГРАММИРОВАНИЕ В MATLAB Содержание Выход
- 109. Типы программных файлов Написание программ – это
- 110. Скрипты Представляют собой последовательности команд Matlab как
- 111. Полезны для автоматизации последовательности действий, которые выполняются
- 112. Функции Специальный вид m-файлов. В отличие от
- 113. Создание функции преследует целью расширение языка. Переменные,
- 114. Структура функции Функция состоит из заголовка и
- 115. Заголовок функции function f = fact(n) Содержание Выход
- 116. Комментарии Используются для пояснения кода; временного исключения
- 117. Можно автоматически закомментировать блок текста. Для этого:
- 118. Создание функции m-файл можно создать в любом
- 119. Использование функции Функция вызывается по своему имени
- 120. Входные и выходные параметры При написании функций
- 121. Содержание Выход
- 122. Подфункции В файлах-функциях Matlab могут быть реально
- 123. Содержание Выход
- 124. Вложенные функции Помимо последовательного вложения в один
- 125. Содержание Выход
- 126. Создание p-кода При вызове m-файла сравнительно много
- 127. Интерактивный ввод данных Используется при написании
- 128. Пример использования input Содержание Выход
- 129. Вывод данных в командное окно Для этого
- 130. Основные языковые конструкции Как и любой процедурный
- 131. Следование Реализуется перечислением каждого из операторов в
- 132. Ветвление Реализуется в двух вариантах: при помощи
- 133. Оператор if Простейшая форма: if end Содержание Выход
- 134. Полный формат оператора if В полном варианте
- 135. Циклы В Matlab имеется два вида циклов:
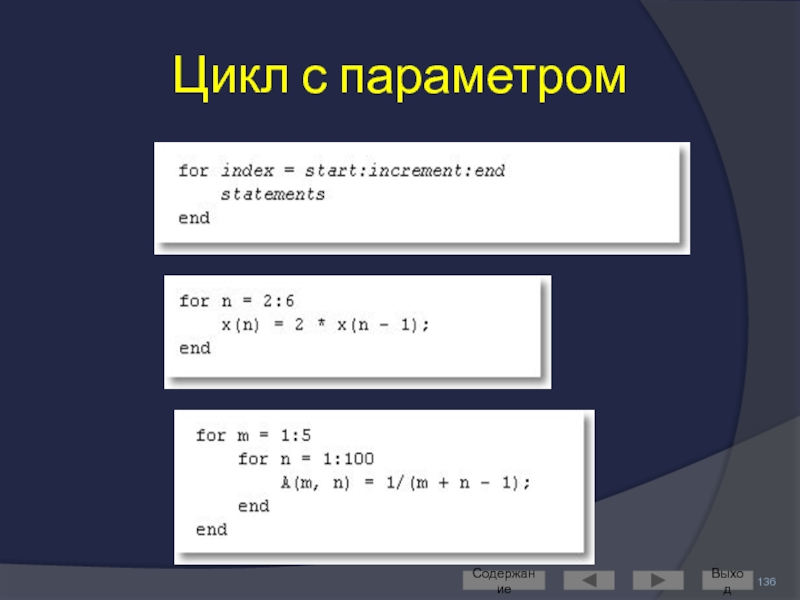
- 136. Цикл с параметром Содержание Выход
- 137. Замечание по использованию цикла с параметром Обычно
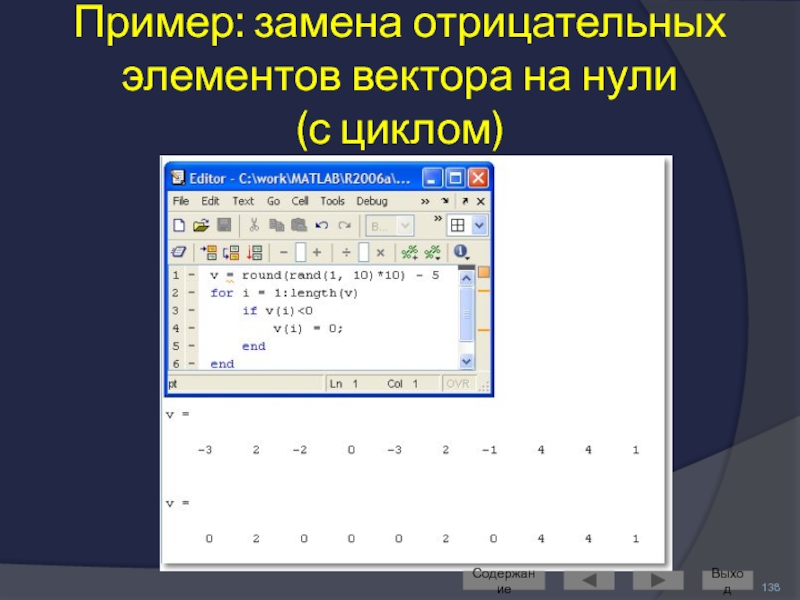
- 138. Пример: замена отрицательных элементов вектора на нули (с циклом) Содержание Выход
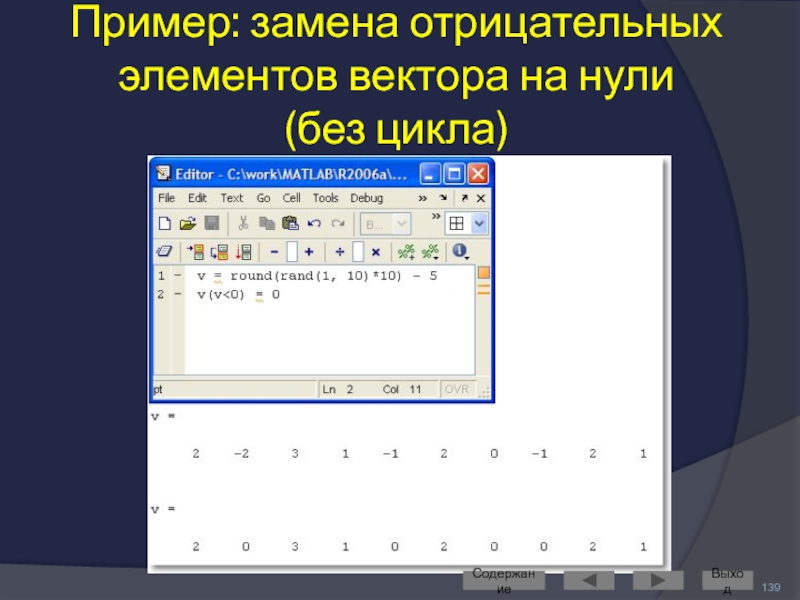
- 139. Пример: замена отрицательных элементов вектора на нули (без цикла) Содержание Выход
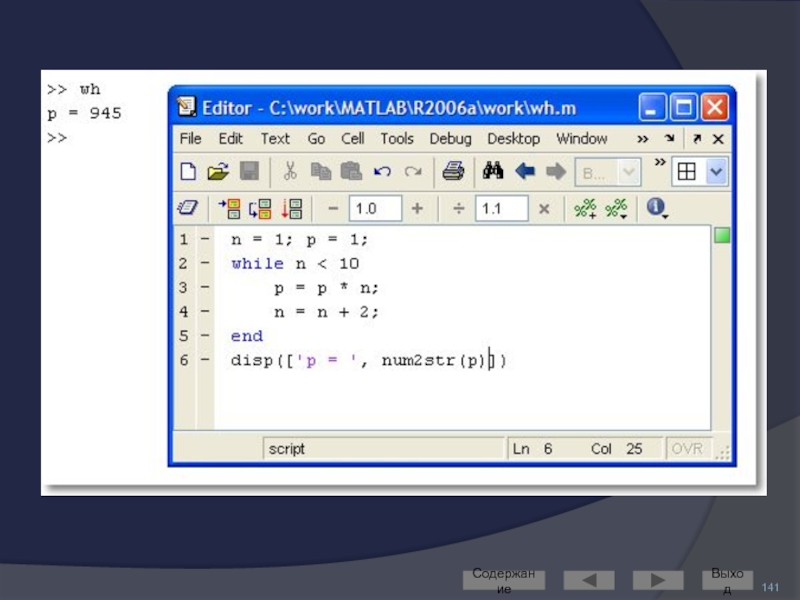
- 140. Цикл с предусловием Синтаксис: while
- 141. Содержание Выход
- 142. Операторы break и continue Аналогичны одноимённым операторам
- 143. Операторы break и continue (пример) Написать скрипт,
- 144. Операторы break и continue (решение) Содержание Выход
- 145. АНАЛИТИЧЕСКИЕ ВЫЧИСЛЕНИЯ В MATLAB Содержание Выход
- 146. Вычисления в Matlab Пример: вычисление определённого интеграла
- 147. Средства Matlab для символьных вычислений Изначально Matlab
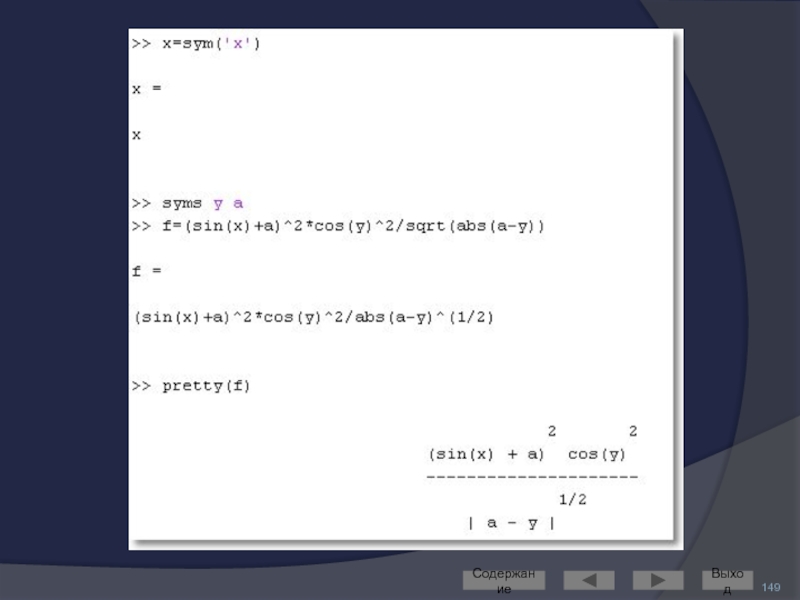
- 148. Создание символьных переменных Для символьного анализа требуется
- 149. Содержание Выход
- 150. Представление символьных переменных Содержание Выход
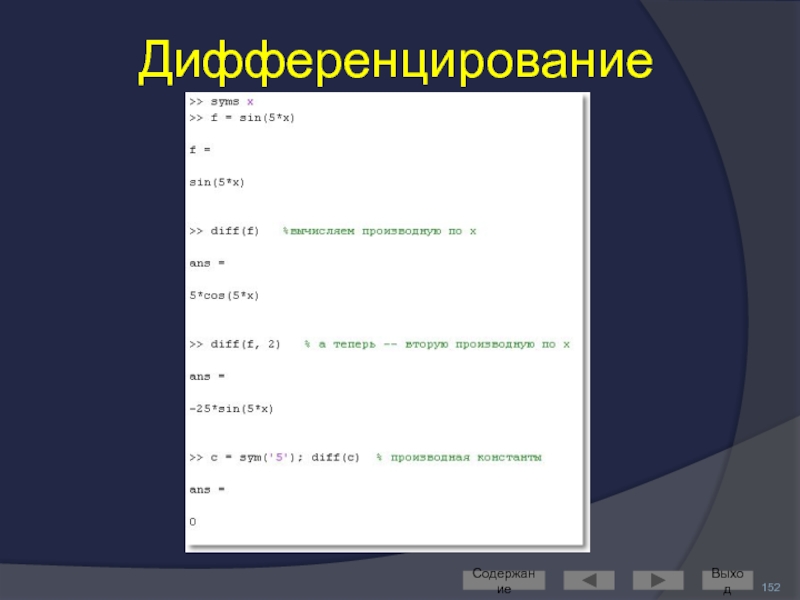
- 151. Символьные вычисления Преобразования математического анализа дифференцирование,
- 152. Дифференцирование Содержание Выход
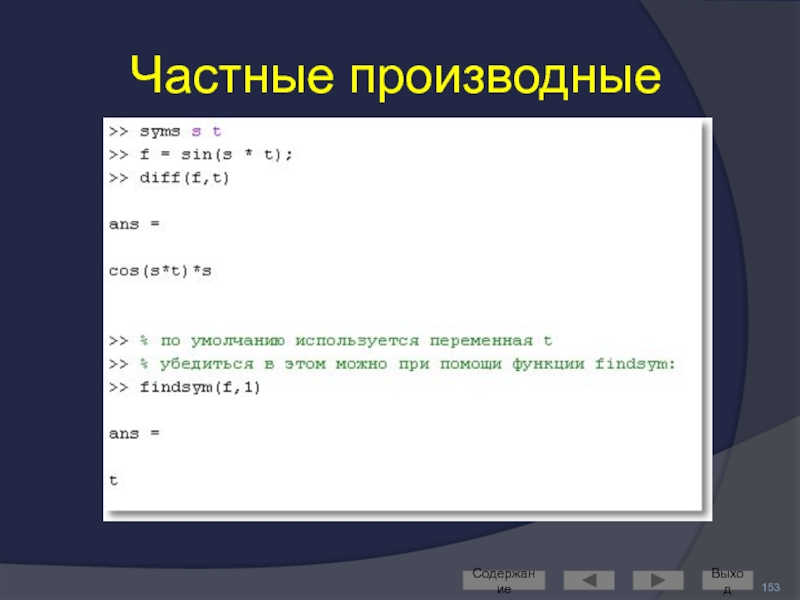
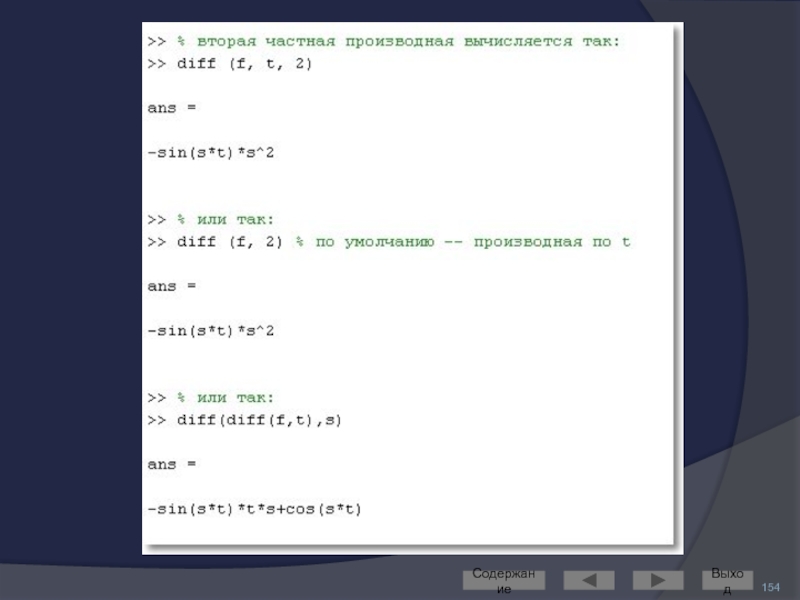
- 153. Частные производные Содержание Выход
- 154. Содержание Выход
- 155. Пределы Содержание Выход
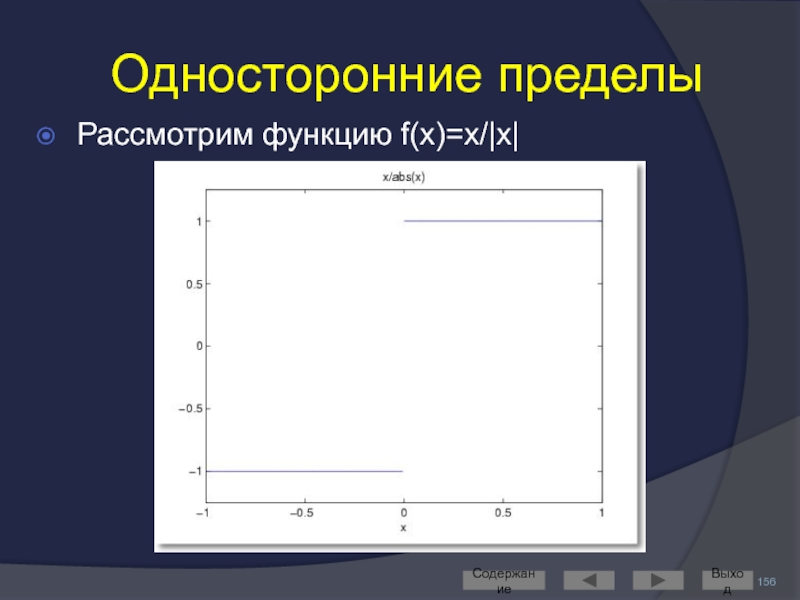
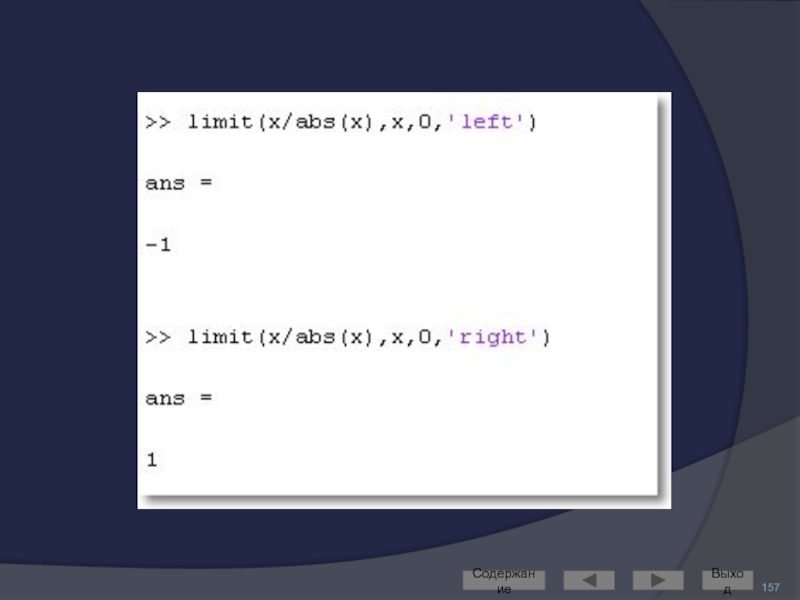
- 156. Односторонние пределы Рассмотрим функцию f(x)=x/|x| Содержание Выход
- 157. Содержание Выход
- 158. Пределы (сводная таблица) Содержание Выход
- 159. Интегралы Содержание Выход
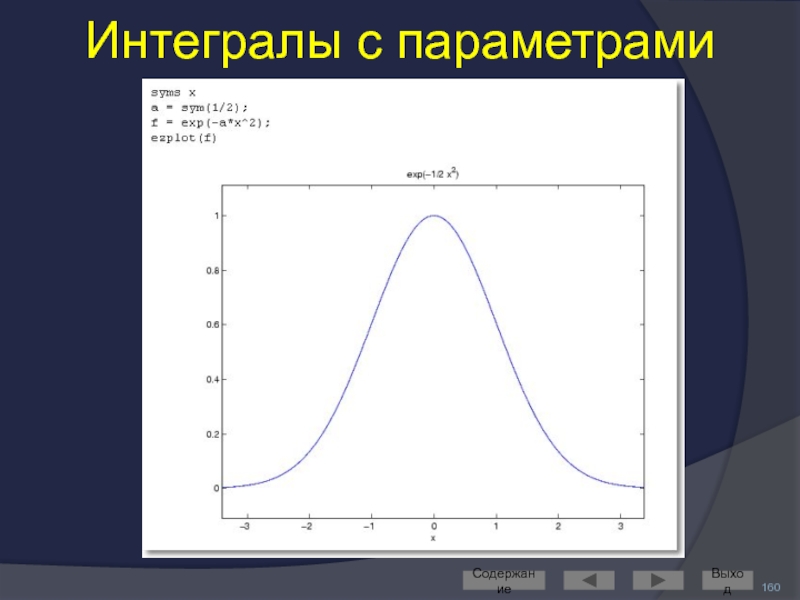
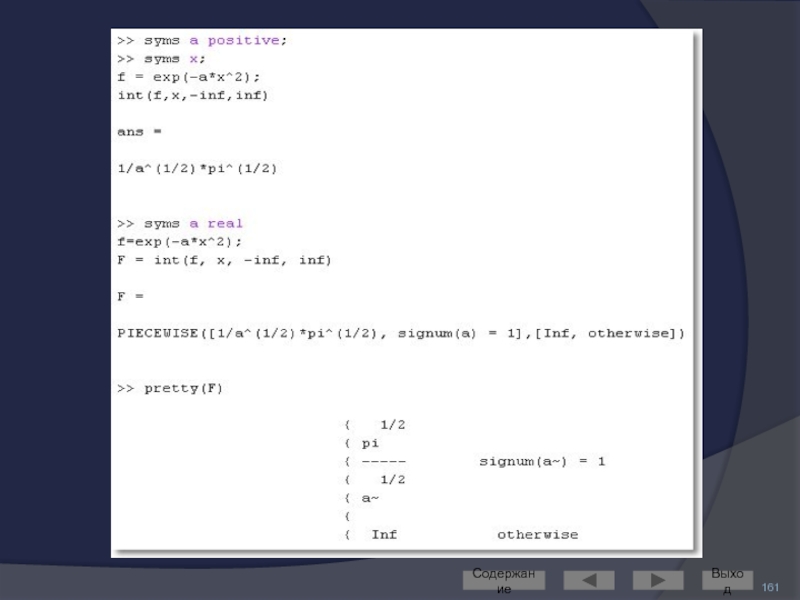
- 160. Интегралы с параметрами Содержание Выход
- 161. Содержание Выход
- 162. Суммирование Содержание Выход
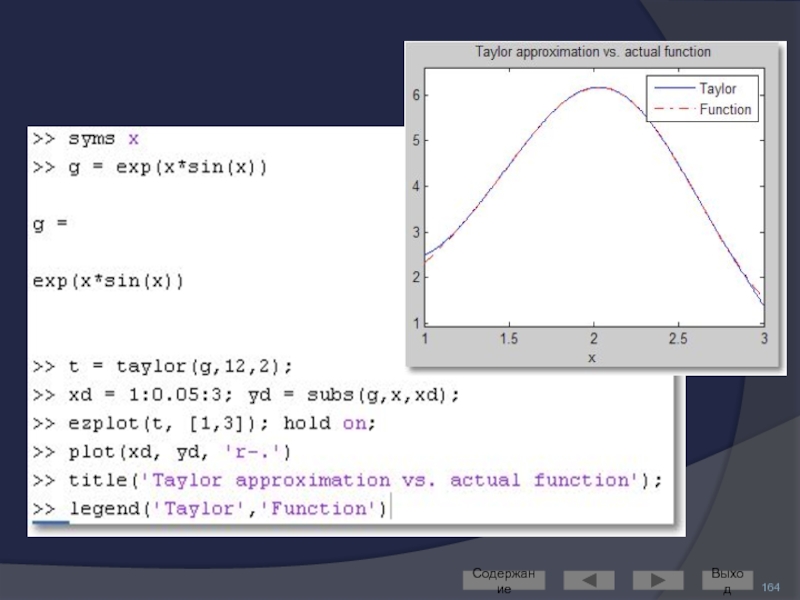
- 163. Разложение в ряд Тейлора Содержание Выход
- 164. Содержание Выход
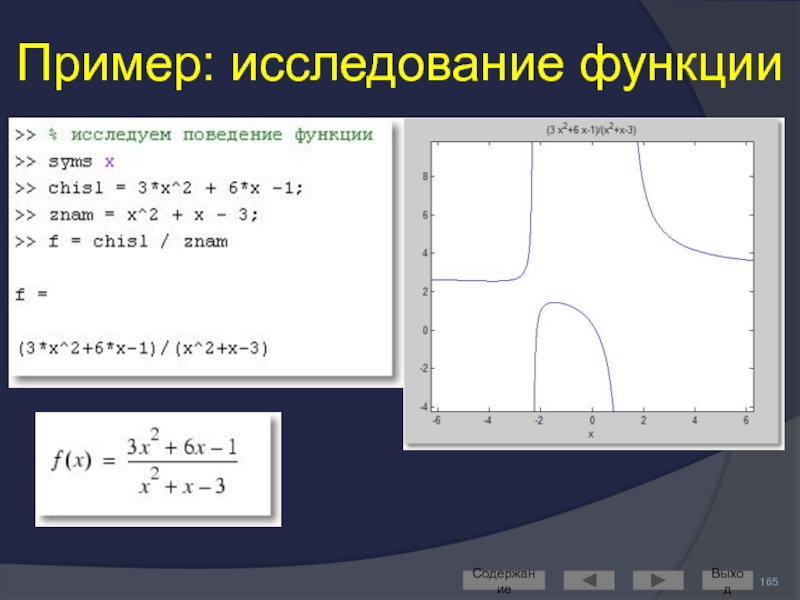
- 165. Пример: исследование функции Содержание Выход
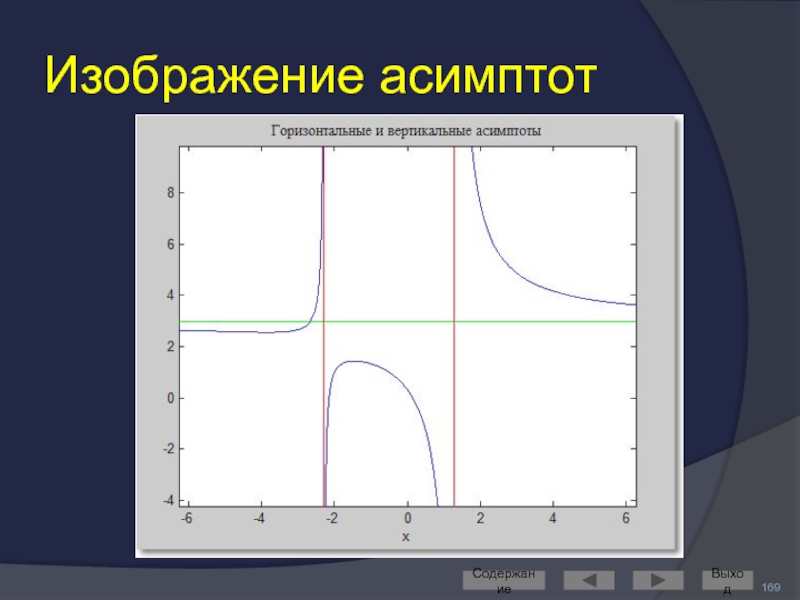
- 166. Найдём горизонтальную асимптоту Содержание Выход
- 167. Найдём вертикальные асимптоты Содержание Выход
- 168. Код для построения асимптот Содержание Выход
- 169. Изображение асимптот Содержание Выход
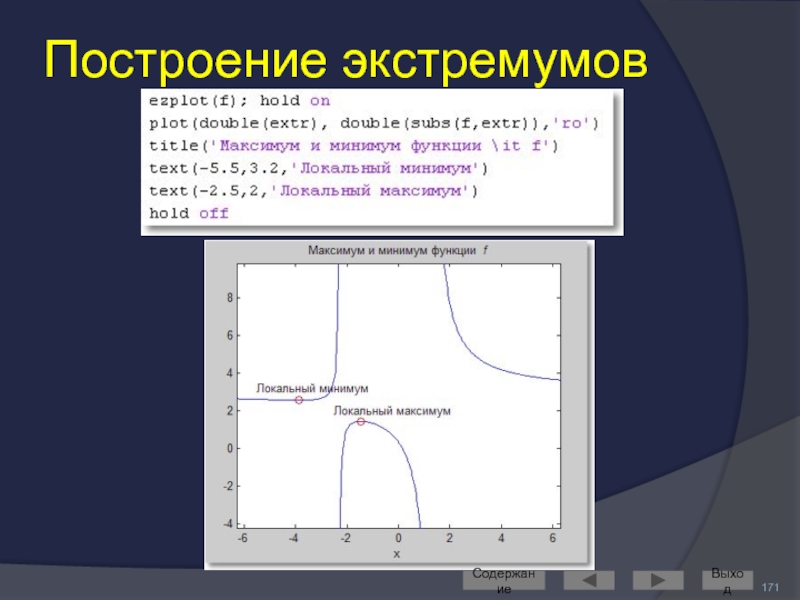
- 170. Экстремумы функции Содержание Выход
- 171. Построение экстремумов Содержание Выход
- 172. Операции над полиномами Реализуются при помощи функций
- 173. collect – вычисляет коэффициенты при степенях независимой
- 174. expand – представляет полином суммой степеней без приведения подобных Содержание Выход
- 175. factor – разлагает полином на множители, если
- 176. Также factor производит каноническое разложение числа: Содержание Выход
- 177. horner – представляет полином в схеме Горнера: Содержание Выход
- 178. Упрощение выражений simplify реализует мощный алгоритм упрощения
- 179. Simplify Содержание Выход
- 180. Simple Содержание Выход
- 181. Simplify против Simple Иногда simple даёт более удачное решение, чем simplify: Содержание Выход
- 182. Simple simple особенно эффективна при работе с тригонометрическими выражениями Содержание Выход
- 183. Подстановка subs подставляет одно символьное выражение в
- 184. Пример подстановки Содержание Выход
- 185. Подстановка значения в функцию Подстановка вместо переменной
- 186. Точная арифметика Точные вычисления реализуются функцией vpa
- 187. Содержание Выход
- 188. Решение уравнений и систем Выполняет команда solve
- 189. Содержание Выход
- 190. Решение систем Также выполняет команда solve Входные
- 191. Содержание Выход
- 192. Решение дифференциальных уравнений Выполняет команда dsolve
- 193. MATLAB В ЗАДАЧАХ ТЕОРИИ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ (ТАУ) Содержание Выход
- 194. Представление и преобразование математических моделей (ММ) динамических
- 195. Задание ДС во вход-выходной (ВВ) форме записи
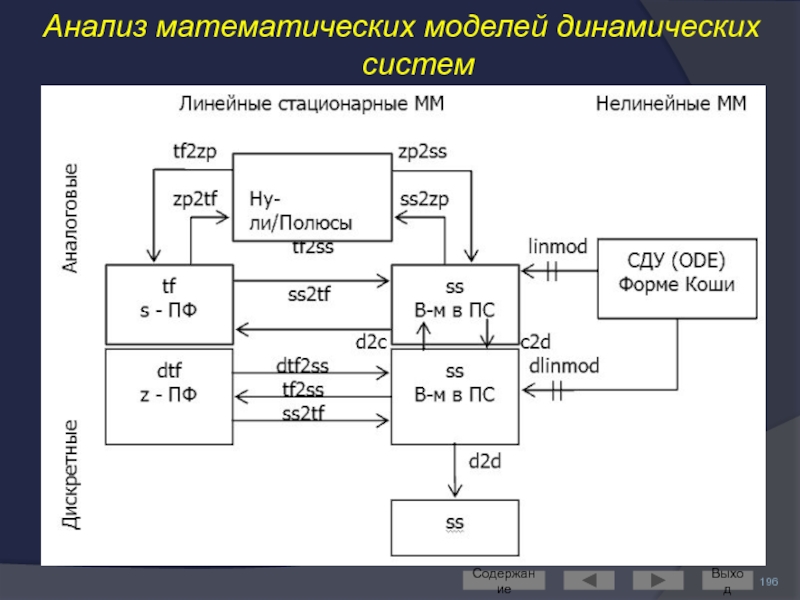
- 196. Анализ математических моделей динамических систем Содержание Выход
- 197. Преобразование ПФ: [NUMc,DENc]=tfchk(NUM,DEN) – проверяет на
- 198. Построение частотных характеристик: [Mod,Fi]=bode(A,B,C,D,ui,w), [Mod,Fi]=bode(NUM,DEN,w) – возвращает
- 199. Вычисление переходных процессов: Y – вектор переходного
- 200. Анализ управляемости: Q=ctrb(A,B) – вычисляет матрицу управляемости
- 201. Анализ наблюдаемости: R=obsv(A,C) – вычисляет матрицу наблюдаемости
- 202. Построение графиков: plot(X,Y,S) – построение графика функции
Слайд 1MATLAB
Ст. преподаватель
кафедры АПП:
Носачёв Сергей Викторович
Каб.297 (главный корпус)
nosachev-s@yandex.ru
Слайд 2Содержание
Введение
Основы Основы Matlab
Вычисления в Вычисления в Matlab
Функции для работы с массивами
Графические
Программирование в Программирование в Matlab
Аналитические вычисления в Аналитические вычисления в Matlab
Слайд 3Matlab (MATrix LABoratory) – это
математические вычисления
создание алгоритмов
моделирование
анализ, обработка и визуализация данных
научная
разработка приложений с GUI
огромное количество прикладных пакетов
Введение
Содержание
Выход
Слайд 4Пакеты, встроенные в Matlab
Matlab Web Server
Bioinformatics Toolbox
Communications Toolbox
Control System Toolbox
Database Toolbox
Distributed
Financial Toolbox
Fuzzy Logic Toolbox
Genetic Algorithm and Direct Search Toolbox
Image Processing Toolbox
Neural Networks Toolbox
Partial Differential Equation Toolbox
Signal Processing Toolbox
SimBiology
Spline Toolbox
Statistics Toolbox
Symbolic Toolbox
Virtual Reality Toolbox
Wavelet Toolbox
Simulink
Aerospace Blockset
Communications Blockset
Video and Image Processing
Real-Time Workshop
Matlab Builder for .NET
Matlab Compiler
Интеграция в MS Office
Содержание
Выход
Слайд 5ОСНОВНЫЕ ЧАСТИ ПАКЕТА MATLAB:
Язык Matlab
Среда Matlab
Управляемая графика
Библиотека математических функций
Программный интерфейс
Содержание
Выход
Слайд 6Язык Matlab
Си- и Паскаль-подобный объектно-ориентированный
Огромный набор встроенных функций
Расширяемый пользователем
Содержание
Выход
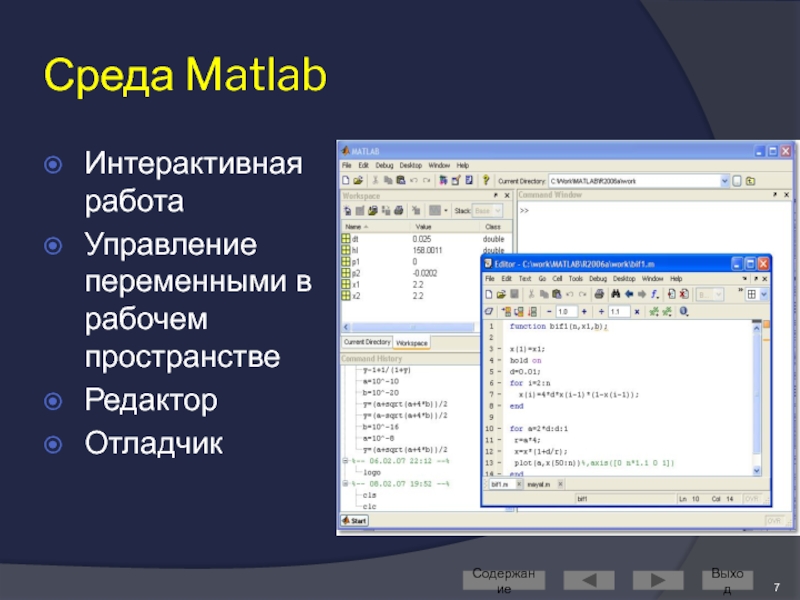
Слайд 7Среда Matlab
Интерактивная работа
Управление переменными в рабочем пространстве
Редактор
Отладчик
Содержание
Выход
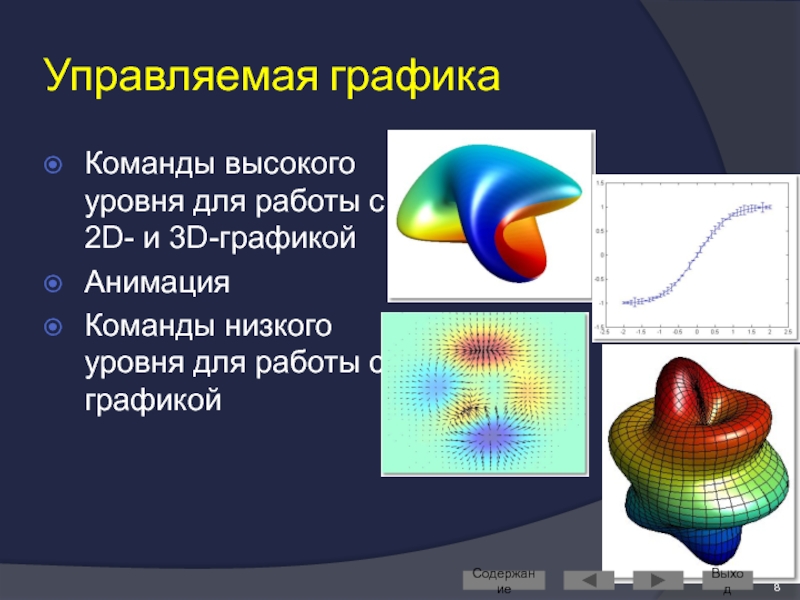
Слайд 8Управляемая графика
Команды высокого уровня для работы с 2D- и 3D-графикой
Анимация
Команды низкого
Содержание
Выход
Слайд 9Библиотека математических функций
Обширная коллекция вычислительных алгоритмов от элементарных функций (sin, cos
обращение матриц
вычисление собственных значений
минимизация функций
дифференцирование
интегрирование
и пр.
Содержание
Выход
Слайд 10Программный интерфейс
API для взаимодействия с программами на языках Си и Фортран
Содержание
Выход
Слайд 11Matlab – язык для работы с матричными объектами
Основной объект Matlab –
Число – это матрица размера (1x1)
Использование матриц
существенно облегчает программирование
делает запись формул краткой и наглядной
В дальнейшем изложении предполагается знакомство с матричной алгеброй и основами программирования
Содержание
Выход
Слайд 12Числа
Основной базовый тип для матриц
Хранятся в формате long (double)
стандарт плавающей
Интервал приблизительно от 10E-308 до 10E+308
Комплексные числа строятся с применением суффиксов i или j (мнимая единица): 2.4e7+3.005i
Содержание
Выход
Слайд 13Другие типы
Строки
Массивы структур (записей)
Массивы ячеек
позволяют объединять в массиве элементы разной природы
Объекты
Содержание
Выход
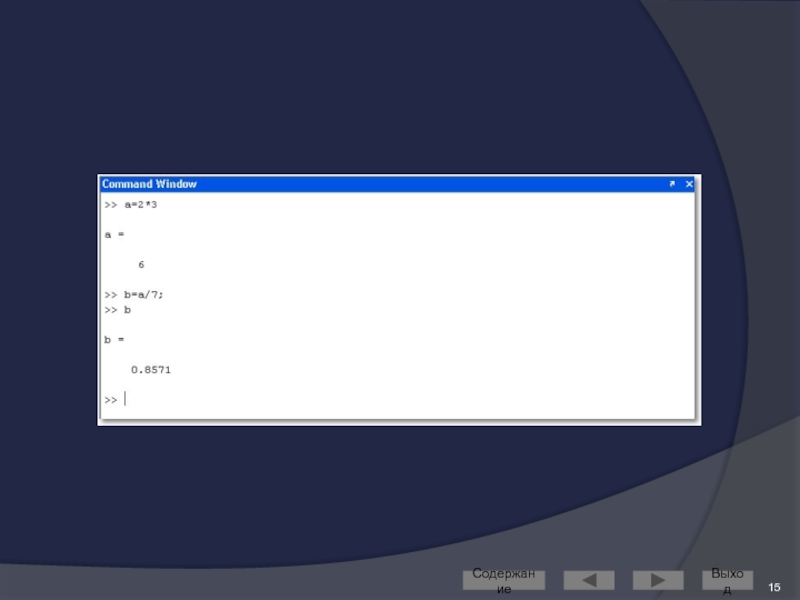
Слайд 14Переменные и выражения
Переменные определяются пользователем при помощи оператора присваивания: x=5
В левой
заглавные и строчные буквы различаются
В правой части оператора присваивания может стоять выражение: y=(2-x)/(x+3)
Если выражение встречается вне оператора присваивания, то его значение вычисляется и помещается в системную переменную ans (от answer)
Переменную ans можно использовать для задания новых выражений: z=ans*3
Если оператор присваивания завершить символом «;», то результат на экране не дублируется; в противном случае – выводится на экран:
Содержание
Выход
Слайд 16Операторы
При составлении выражений могут быть использованы операторы:
+ сложение
-
* умножение
/ деление
^ возведение в степень
Приоритет операций обычный. Изменяется при помощи круглых скобок
Содержание
Выход
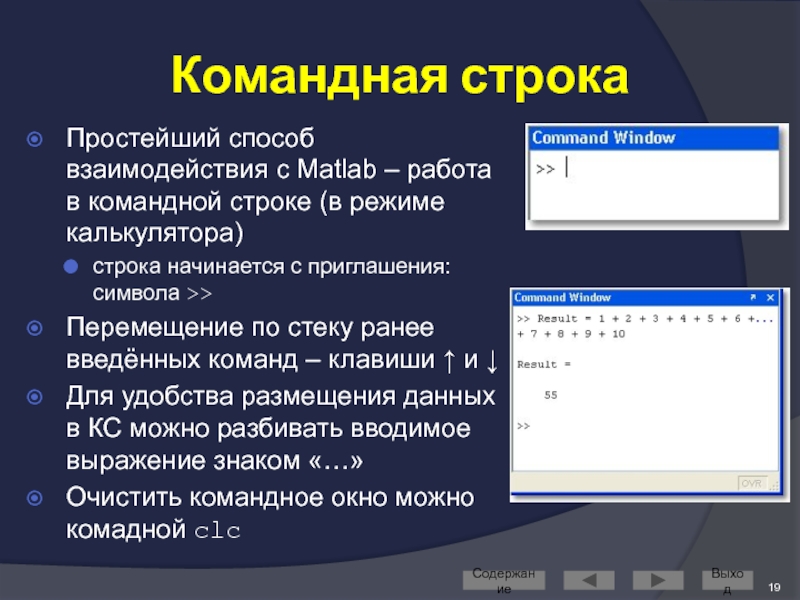
Слайд 19Командная строка
Простейший способ взаимодействия с Matlab – работа в командной строке
строка начинается с приглашения: символа >>
Перемещение по стеку ранее введённых команд – клавиши ↑ и ↓
Для удобства размещения данных в КС можно разбивать вводимое выражение знаком «…»
Очистить командное окно можно комадной clc
Содержание
Выход
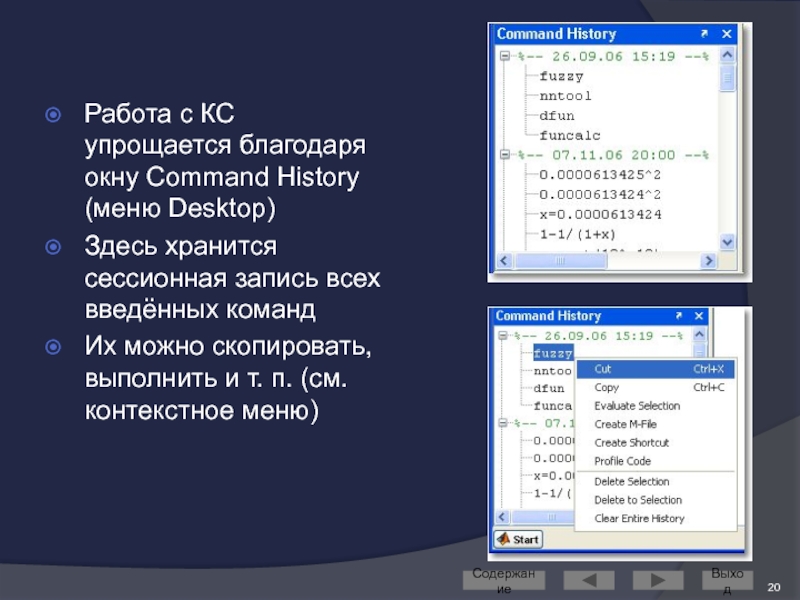
Слайд 20Работа с КС упрощается благодаря окну Command History (меню Desktop)
Здесь хранится
Их можно скопировать, выполнить и т. п. (см. контекстное меню)
Содержание
Выход
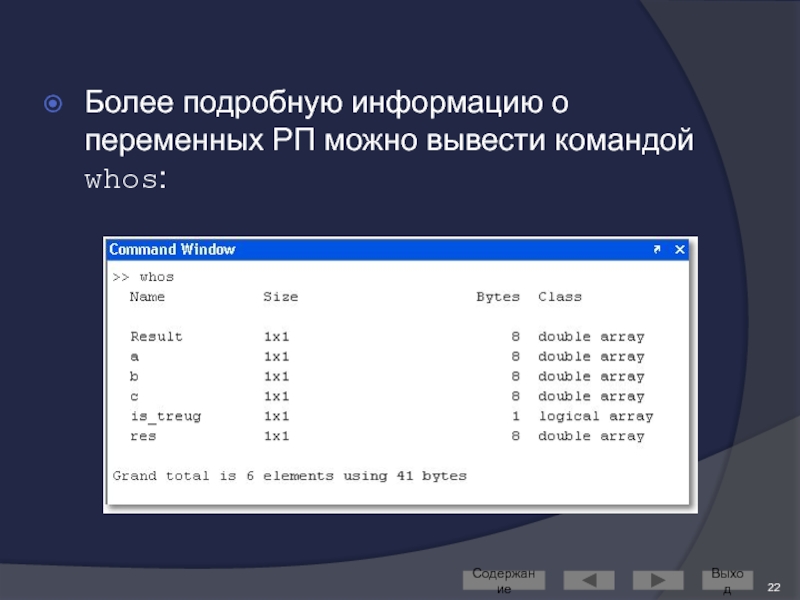
Слайд 21Рабочее пространство (Workspace)
Все переменные хранятся в РП
порой это отнимает много места
Просмотреть
Содержание
Выход
Слайд 23После закрытия сеанса работы MATLABа все переменные, вычисленные в течение сеанса,
командой меню: File \ Save Workspace As…
командой Matlab: save
Содержание
Выход
Слайд 24Команда save
save – сохраняет все переменные в файл matlab.mat
save filename –
save filename x y z – сохраняет переменные x, y, z в файл filename (можно по маске: a*)
save filename x y z -ASCII – сохраняет переменные x, y, z в файл filename в текстовом виде
save('filename’, ‘a',‘b','-ASCII') – процедурная форма вызова команды
параметры – в виде строк (в одинарных апострофах)
Подробнее про эту и любую другую команду Matlab
help <имя команды>
или F1
Содержание
Выход
Слайд 25Команда load
Служит для загрузки ранее сохранённых данных
load – загружает все переменные
load filename – загружает все переменные из файла filename
load filename x y z – загружает переменные x, y, z из файла filename
load -ASCII filename x y z– загружает переменные x, y, z из текстового файла filename load('filename’, ‘a',‘b','-ASCII') – процедурная форма вызова команды
Содержание
Выход
Слайд 26Команда clear
Служит для удаления переменных из РП
clear – удаляет все переменные
clear
clear x y z – удаляет переменные x, y и z.
Содержание
Выход
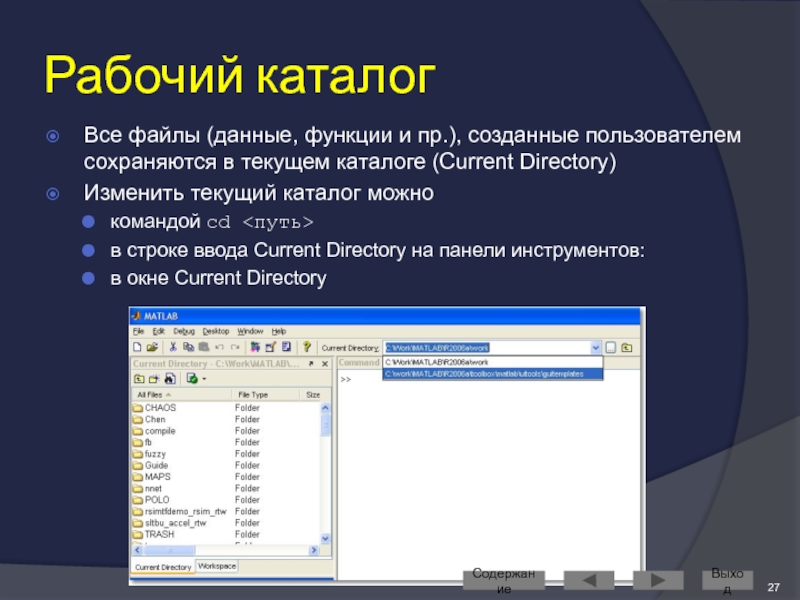
Слайд 27Рабочий каталог
Все файлы (данные, функции и пр.), созданные пользователем сохраняются в
Изменить текущий каталог можно
командой cd <путь>
в строке ввода Current Directory на панели инструментов:
в окне Current Directory
Содержание
Выход
Слайд 28Сохранение рабочей сессии
diary – сохраняет лог текущей сессии (весь текстовый ввод
По умолчанию – в файл diary в текущем каталоге
diary filename или diary(‘filename’) – сохраняют сессию в указанном файле
diary off / diary on – соответственно, приостанавливают и продолжают ведение лога
diary – переключается между режимами on/off, если лог уже ведётся
Содержание
Выход
Слайд 30Элементарные функции
Тригонометрические
sin
cos
tan
cot
asin
acos
atan
acot
sinh
cosh
tanh
coth
asinh
acosh
atanh
acoth
sind
cosd
tand
cotd
Содержание
Выход
Слайд 32Элементарные функции
Округление и остатки
fix – округление к нулю
floor – округление к
ceil – округление к плюс бесконечности
round – округление к ближайшему целому
mod(x,y) – остаток от деления x на y без учёта знака (x - n*y, где n = floor(x/y))
rem(x,y) – остаток от деления x на y с учётом знака (x - n*y, где n = fix(x/y))
Содержание
Выход
Слайд 33Элементарные функции
Комплексные числа
abs(z) – модуль комплексного числа z
angle(z) – фаза z
real(z) – действительная часть z
imag(z) – мнимая часть z
conj(z) – комплексно сопряжённое число для z
complex(a,b) – конструирует комплексное число a+ib
isreal(z) – возвращает истину, если z – действительное
Содержание
Выход
Слайд 34Элементарные функции
Просмотреть полный список элементарных функций можно командой
help elfun
Содержание
Выход
Слайд 35Константы
pi – число pi
Inf – бесконечность
-Inf – минус бесконечность
NaN (Not a
Содержание
Выход
Слайд 36Одномерные массивы
Задание массива:
a = [ -3 4 2];
a = [ -3,
Диапазоны:
b = -3: 2 (b = -3 -2 -1 0 1 2)
b = -3:2:5 (b = -3 -1 1 3 5)
Доступ к элементу:
a(3) (будет равно 2)
Изменение элемента:
a(3) = 1
Количество элементов в массиве: length(a) (будет равно 3)
Нумерация элементов начинается с 1
Добавление элементов в массив
a(4) = 5;
a = [a 5]
Конкатенация массивов:
c = [a b]
Удаление массива (превращение в пустой массив)
a = [ ]
Содержание
Выход
Слайд 38Векторы-столбцы и
векторы-строки
Любая строка и столбец матрицы – это вектор
Векторы, расположенные вдоль
Векторы, расположенные вдоль столбцов – векторы-столбцы (размер nx1)
Задание вектора-столбца:
К векторам любого типа применима функция length
Содержание
Выход
Слайд 39Размерность и размер матриц
Размерность массива определяется функцией ndims(A)
Размер массива – функцией
Содержание
Выход
Слайд 40Конкатенация
Рассмотрим две матрицы
Проведём склейку «в столбик», а затем «в строку»:
При несовпадении
Содержание
Выход
Слайд 41Диапазоны
Можно использовать как для задания значений векторов, так и для задания
Рассмотрим другие примеры
Содержание
Выход
Слайд 43Для обращения к последнему элементу любой размерности можно использовать служебное слово
Содержание
Выход
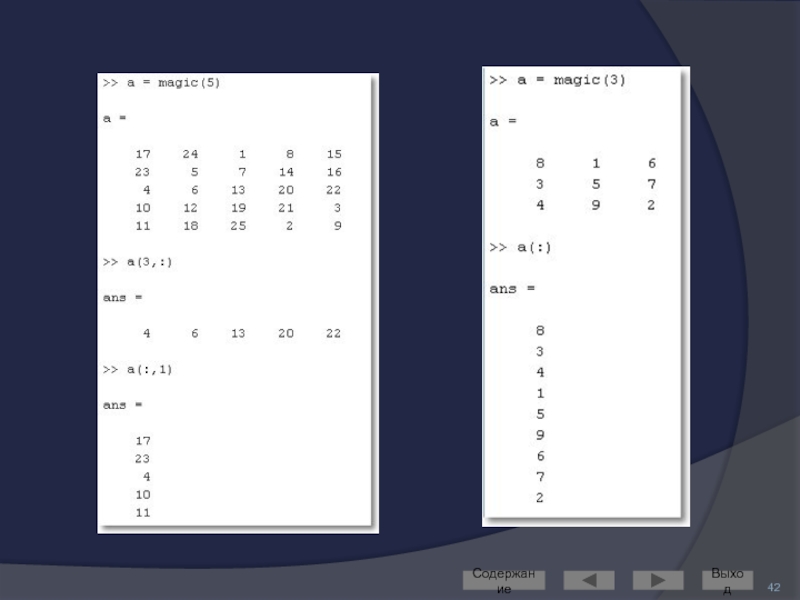
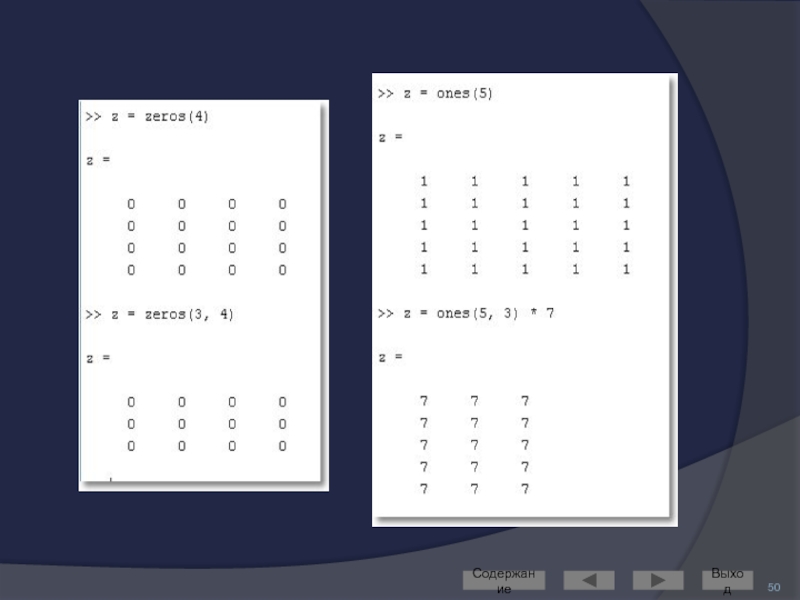
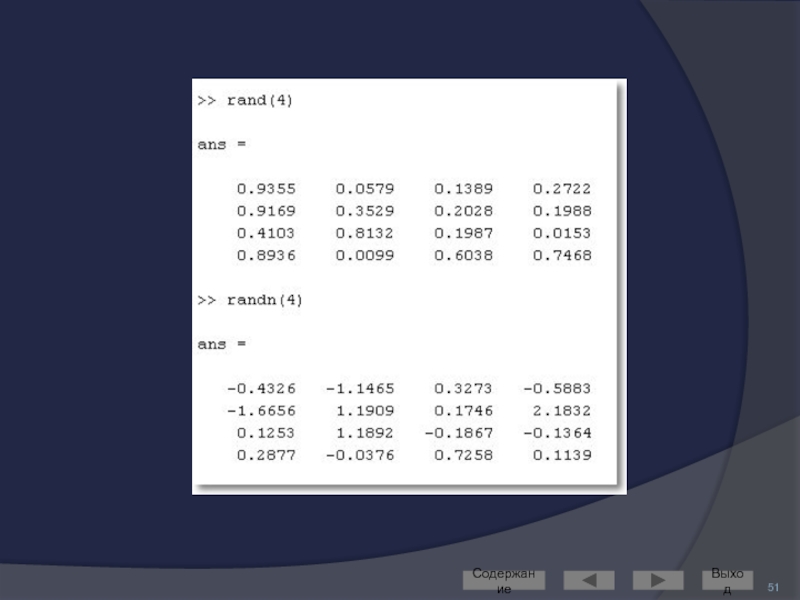
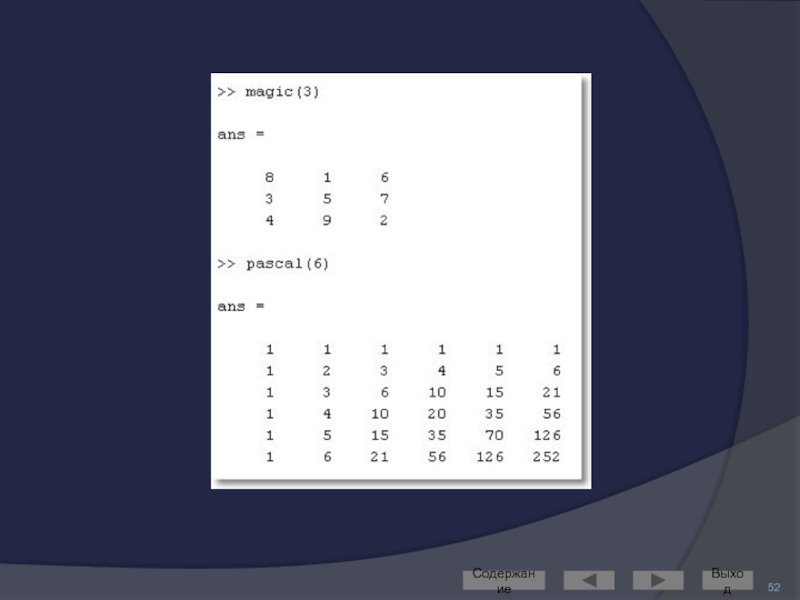
Слайд 47Создание матриц
специального вида
Для работы с матрицами удобно пользоваться следующими функциями
ones –
zeros – формирование массива из нулей
eye – формирование единичной матрицы
rand – формирование матрицы из числе, равномерно распределённых на отрезке [0, 1]
randn – формирование матрицы из чисел, нормально распределённых с математическим ожиданием 0.
magic – формирование магического квадрата
pascal – формирование квадрата Паскаля
diag – диагональная матрица
и др.
Содержание
Выход
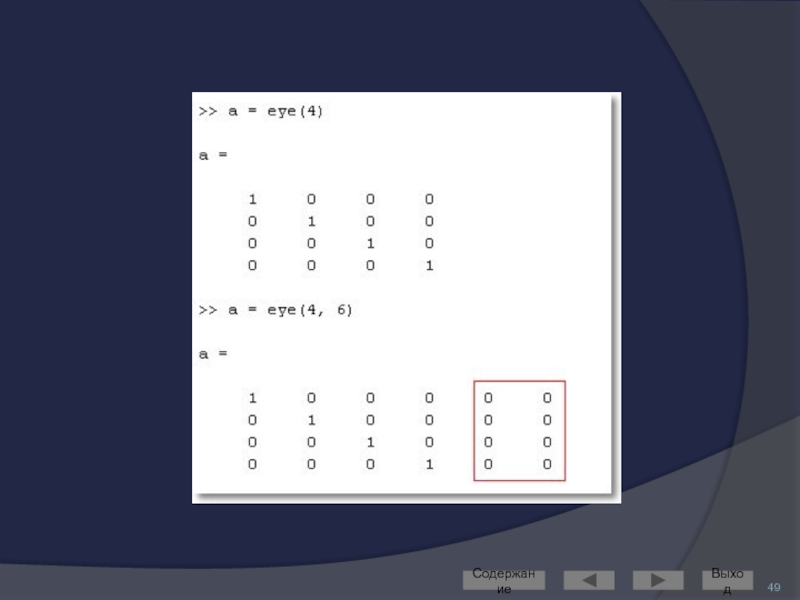
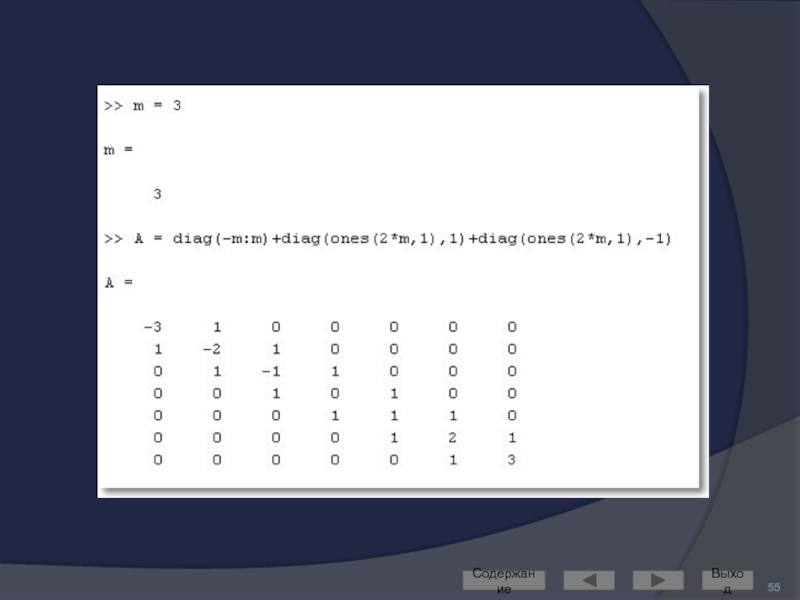
Слайд 48МАТРИЦЫ СПЕЦИАЛЬНОГО ВИДА
Рассмотрим основной синтаксис на примере функции создания единичной матрицы
eye(m) – создание единичной матрицы размера [m, m]
eye(m, n) – создание единичной матрицы размера [m, n]
«лишние» строки или столбцы дополняются нулями
Содержание
Выход
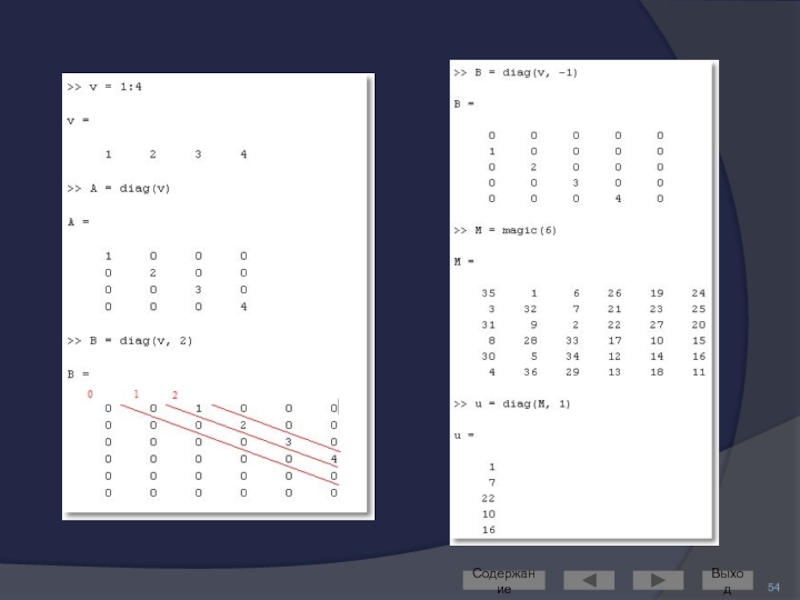
Слайд 53Функция diag: работа с диагональными матрицами
у которых ненулевые элементы расположены на
Синтаксис:
X = diag(v) – на главной диагонали матрицы X расположены элементы вектора v
X = diag(v,k) – на k-ой диагонали матрицы X расположены элементы вектора v (по умолчанию k=0)
v = diag(X,k) – извлечь из матрицы X k-ую диагональ и сохранить её в векторе v
Содержание
Выход
Слайд 56ВЫЧИСЛЕНИЯ С ЭЛЕМЕНТАМИ МАССИВОВ
Простейшие операции над элементами массивов:
sum: сумма элементов
prod: произведение
cumsum: кумулятивная сумма элементов
cumprod: кумулятивное произведение элементов
max: нахождение максимального элемента
min: нахождение минимального элемента
sort: сортировка элементов
Содержание
Выход
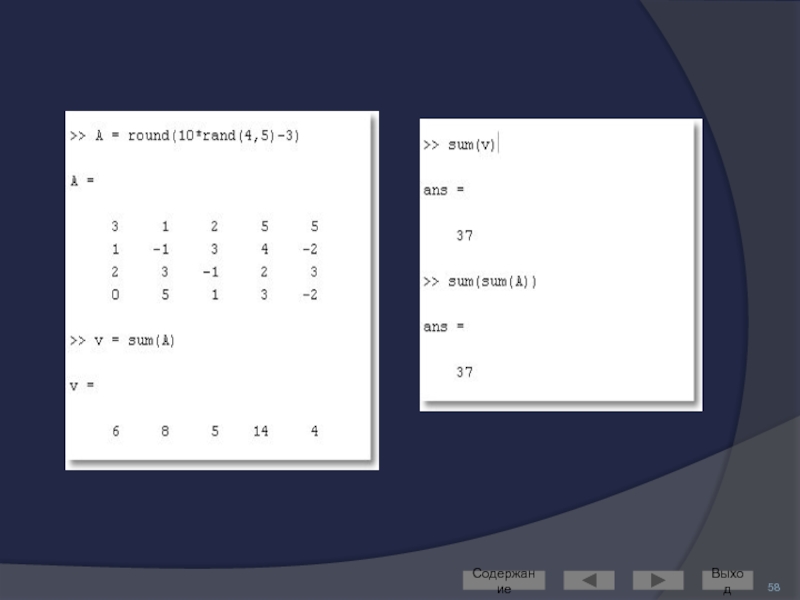
Слайд 57Рассмотрим работу некоторых из этих функций на примере sum
Для векторов эта
Для массивов – сумму элементов по каждому из столбцов
результат – вектор-строка
Остальные функции работают по этому же принципу
Содержание
Выход
Слайд 59Кумулятивная сумма вычисляется так же, только происходит накопление вычисленных значений в
Содержание
Выход
Слайд 61Вызов функций max/min с двумя выходными параметрами позволяет определить и индекс
Содержание
Выход
Слайд 63ЛОГИЧЕСКИЕ ФУНКЦИИ
All(v) – возвращает истину, если все элементы вектора v отличны
Содержание
Выход
Слайд 64Any(v) – возвращает истину, если хотя бы один элемент вектора v
Содержание
Выход
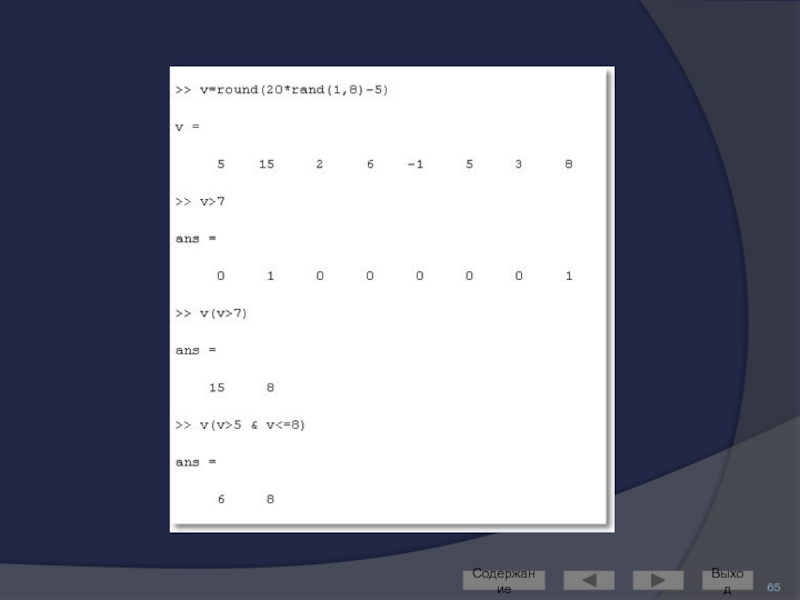
Слайд 66Поиск в массиве
find: определяет индексы элементов, удовлетворяющих заданному условию
Содержание
Выход
Слайд 68Математические матричные операции
det – вычисление определителя квадратной матрицы
Содержание
Выход
Слайд 69МАТРИЧНЫЕ И ПОЭЛЕМЕНТНЫЕ ОПЕРАЦИИ
При работе с матрицами можно использовать два вида
матричные: производят действия по правилам матричной алгебры
поэлементные: производят действия над соответствующими элементами матриц
размеры матриц должны быть одинаковыми
от матричных операций отличаются точкой перед знаком операции
Содержание
Выход
Слайд 70‘ транспонирование
+ матричное (и поэлементное) сложение
- матричное (и поэлементное) вычитание
*
/ матричное деление
^ матричное возведение в степень
\ матричное деление «слева»
.* поэлементное умножение
./ поэлементное деление
.^ поэлементное возведение в степень
.\ поэлементное деление «слева»
Содержание
Выход
Слайд 72Такие операции часто используются, если нужно применить какую либо функцию ко
Содержание
Выход
Слайд 74Операции «деления» слева и справа
Применяются для решения систем линейных уравнений (СЛУ)
Деление
для квадратных матриц реализует метод Гаусса
для прямоугольных матриц– метод наименьших квадратов
Содержание
Выход
Слайд 76Графика в Matlab
Высокоуровневая
не требует от пользователя детальных знаний о работе
Объектная
каждый объект на рисунке имеет свойства, которые можно менять
Управляемая (handled)
доступ к графическим объектам возможен как через инспектор объектов, так и при помощи встроенных функций (дескрипторная графика)
Содержание
Выход
Слайд 77Двумерные (2D-) графики
Простейший способ построения 2D-графика:
задать область построения (диапазон);
вычислить значение функции
построить график при помощи одной из встроенных функций Matlab
Содержание
Выход
Слайд 79Построение второго графика
Если сразу же построить другой график, то старый график
Содержание
Выход
Слайд 80Построение двух графиков в одной системе координат
Два графика в одной СК
«закрепить» графическое окно при помощи команды hold on
применить одну команду plot
Содержание
Выход
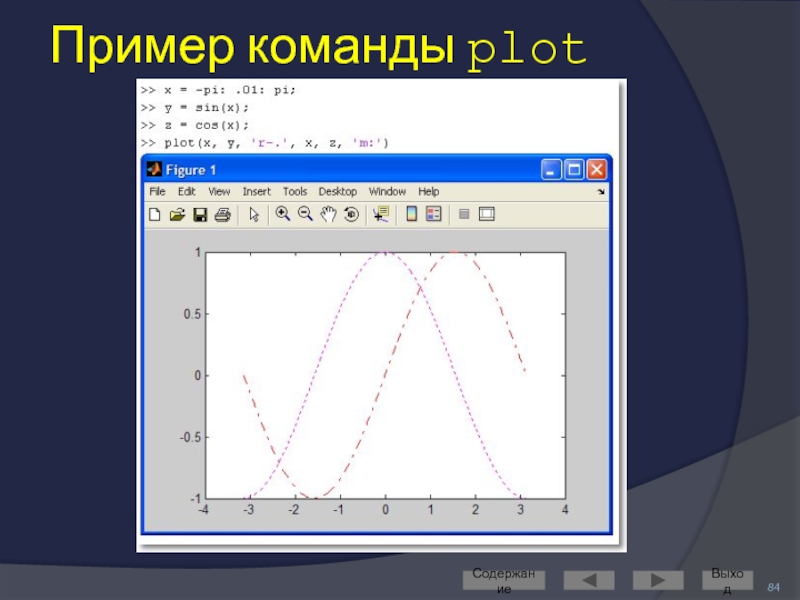
Слайд 83В команде plot можно задать для каждого графика
цвет линии
Содержание
Выход
Дополнительные параметры команды plot
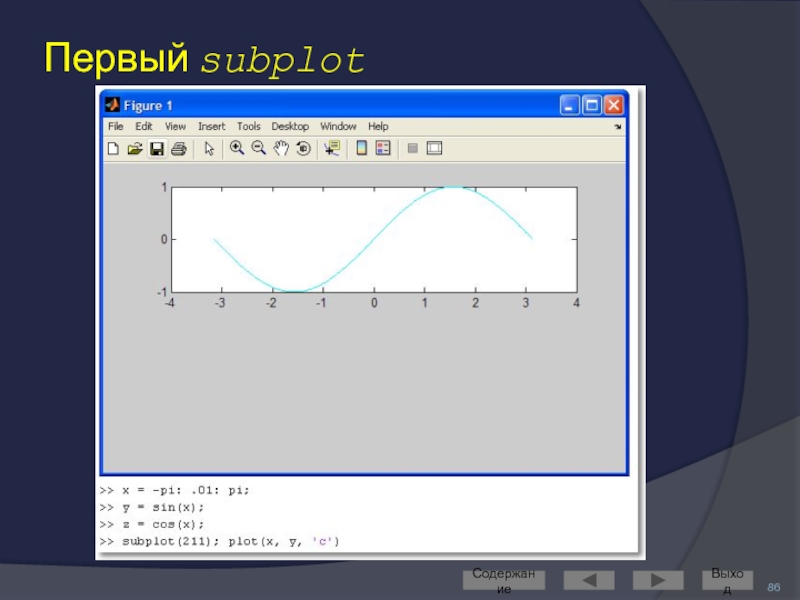
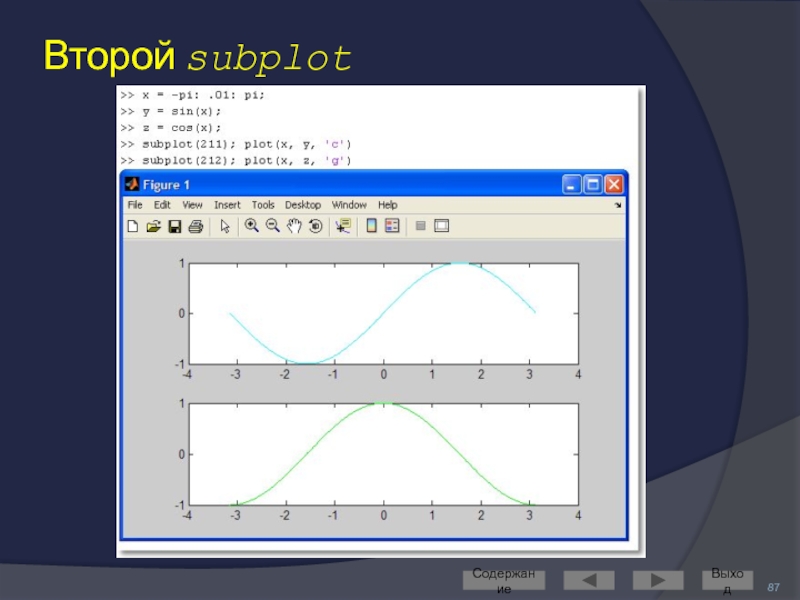
Слайд 85Построение нескольких графиков в одном окне в разных СК
Поверхность графического окна
Для этого служит команда subplot
В качестве параметров ей передаётся трёхзначное целое число вида mnk
m и n определяют количество графических «подокон» по горизонтали и вертикали
k задаёт номер графического «подокна»
порядок нумерации – по строкам
Содержание
Выход
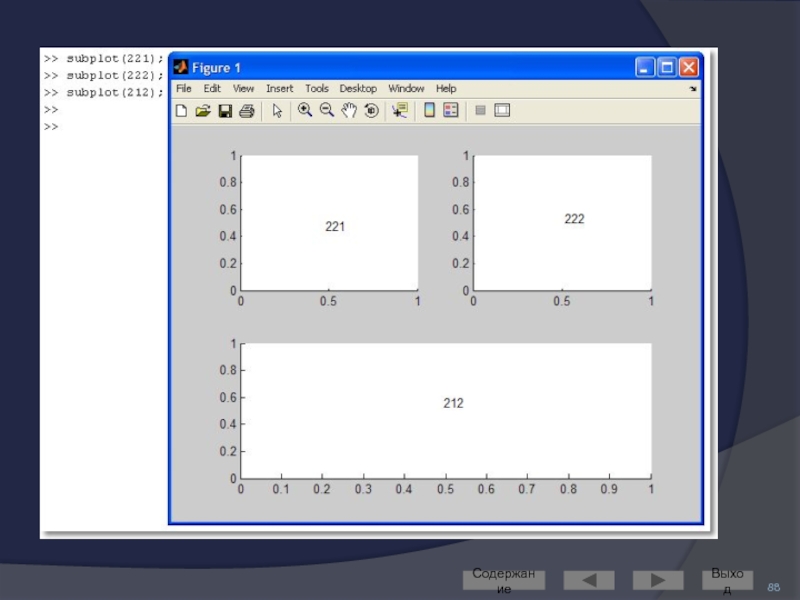
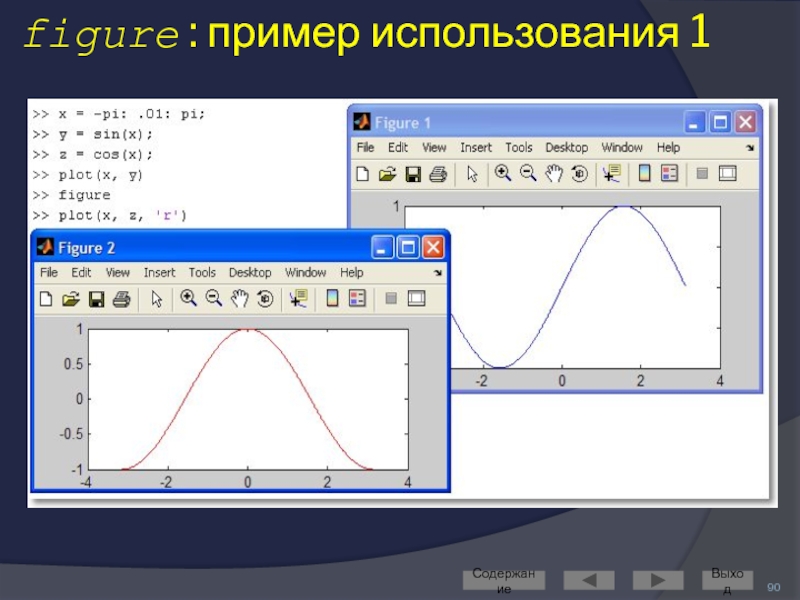
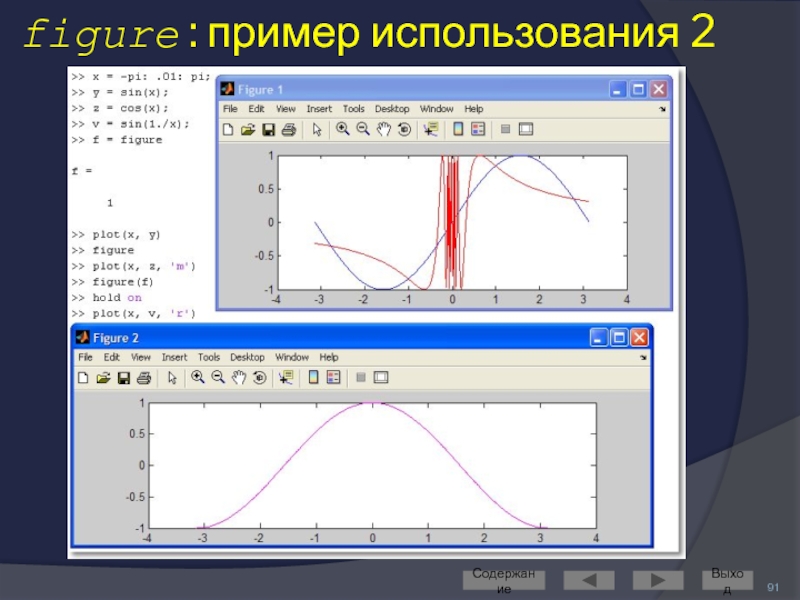
Слайд 89Построение графиков в разных графических окнах
Создать новое графическое окно можно командой
Команда figure создаёт графическое окно и возвращает указатель на него:
h = figure
Активизировать ранее созданное окно можно командой figure(h)
Содержание
Выход
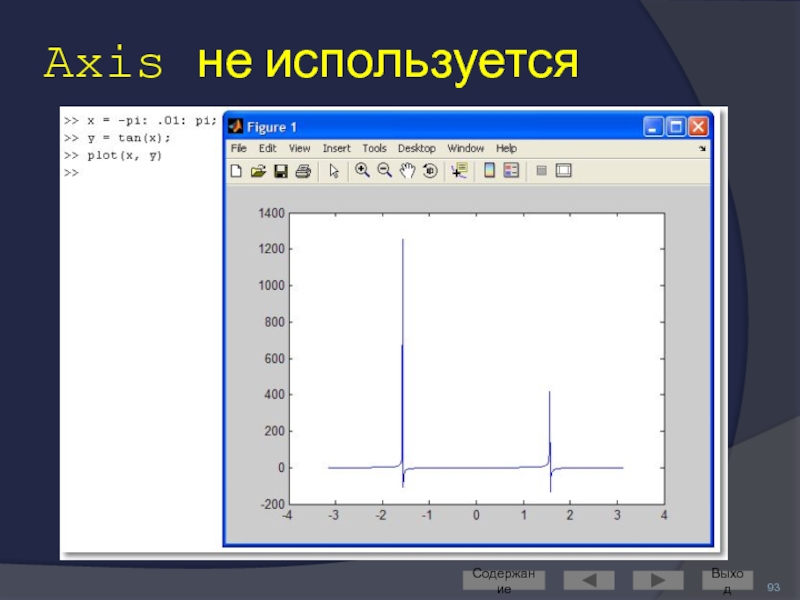
Слайд 92Axis: управление масштабом
Команда
axis([Xmin Xmax Ymin Ymax]) задаёт область построения графиков
Используется, если результат автомасштабирования неудовлетворителен
Содержание
Выход
Слайд 95Оформление графиков
Для графиков можно задать
масштабную сетку: grid on
заголовок: title(’заголовок’)
подписи осей: xlabel(’текст’)
В заголовках и подписях можно использовать нотацию системы TeX
Содержание
Выход
Слайд 98Графики функций, заданных параметрически
Строятся при помощи оператора plot
Вначале задаётся диапазон построения
Затем вычисляются x(t) и y(t)
И строится график
Содержание
Выход
Слайд 100Графики параметрических функций часто возникают в физических приложениях
Независимая переменная t в
Для построения динамического графика можно использовать функцию comet(x,y)
Содержание
Выход
Слайд 101Функции в полярной СК
Строятся аналогично графикам функций в декартовой системе
Для построения
Содержание
Выход
Слайд 103Построение
поверхностей
контурных диаграмм (линии равного уровня)
3D-линий
векторных полей
скалярных полей
и др.
Трёхмерная (3D-)
Содержание
Выход
Слайд 105Построение 3D-поверхности
Рассмотрим пример:
построить поверхность f(x,y)=sin(r)/r, где r=sqrt(x2+y2)
Содержание
Выход
Слайд 106Функция meshgrid возвращает две матрицы – X и Y – которые
Если диапазоны по X и Y разные, то функции передаются два диапазона
Собственно поверхность выводится функцией surfl
Содержание
Выход
Слайд 107Функции для построения поверхностей
О других графических функциях можно узнать в системе
Содержание
Выход
Слайд 109Типы программных файлов
Написание программ – это альтернатива работе в командной строке
Программный
m-файлы бывают двух видов:
скрипты (scripts)
функции (functions)
Содержание
Выход
Слайд 110Скрипты
Представляют собой последовательности команд Matlab
как если бы мы перенесли их из
Вызываются по имени через командную строку.
Выполняются в режиме построчного анализа, обработки и выполнения исходных команд
Содержание
Выход
Слайд 111Полезны для автоматизации последовательности действий, которые выполняются многократно.
Не могут принимать параметры
Хранят значения своих переменных в рабочем пространстве
где переменные доступны для других скриптов и из командной строки
Содержание
Выход
Слайд 112Функции
Специальный вид m-файлов.
В отличие от скриптов могут принимать аргументы и возвращать
Использование функций позволяет
структурировать программу
избежать повторения кода
Содержание
Выход
Слайд 113Создание функции преследует целью расширение языка.
Переменные, определённые внутри функции являются локальными
то
Функция имеет собственное имя.
Кроме того, с ней связано имя m-файла, в котором функция записана
будем соблюдать правило: имя функции и имя m-файла должны быть одинаковы
Содержание
Выход
Слайд 114Структура функции
Функция состоит из заголовка и тела
function f = fact(n)
% Вычисляет факториал. Линия H1
% FACT(N) возвращает N!, Help
f = prod(1:n); Тело функции
H1 и Help выводятся по команде help <имя функции>
Фактически, функция отличается от скрипта наличием заголовка и способом вызова
Содержание
Выход
Слайд 116Комментарии
Используются для
пояснения кода;
временного исключения кода из текста.
Могут быть строчными и блочными
Строчные
с этого места и до конца строки всё игнорируется компилятором % как в этом примере
Блочные начинаются с символа «%{» и заканчиваются символом «%}»:
%{
эти символы должны обязательно стоять в отдельных строках!
%}
Содержание
Выход
Слайд 117Можно автоматически закомментировать блок текста. Для этого:
выделить блок
щёлкнуть правой кнопкой
выбрать Comment
Снять комментарий:
выделить закомментированный блок
щёлкнуть правой кнопкой
выбрать Uncomment (или Ctrl+T)
Содержание
Выход
Слайд 118Создание функции
m-файл можно создать в любом текстовом редакторе.
Например, во встроенном редакторе
при
или командой
edit <имя файла>
Содержание
Выход
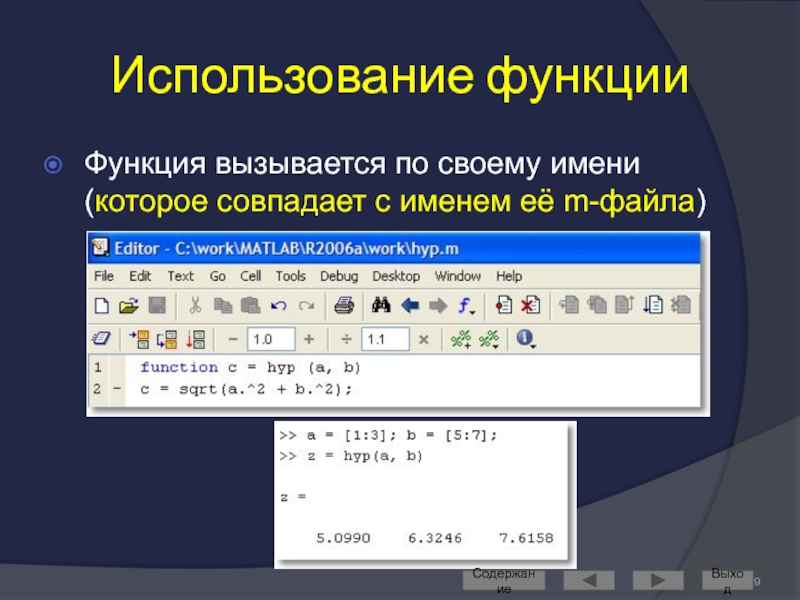
Слайд 119Использование функции
Функция вызывается по своему имени (которое совпадает с именем её
Содержание
Выход
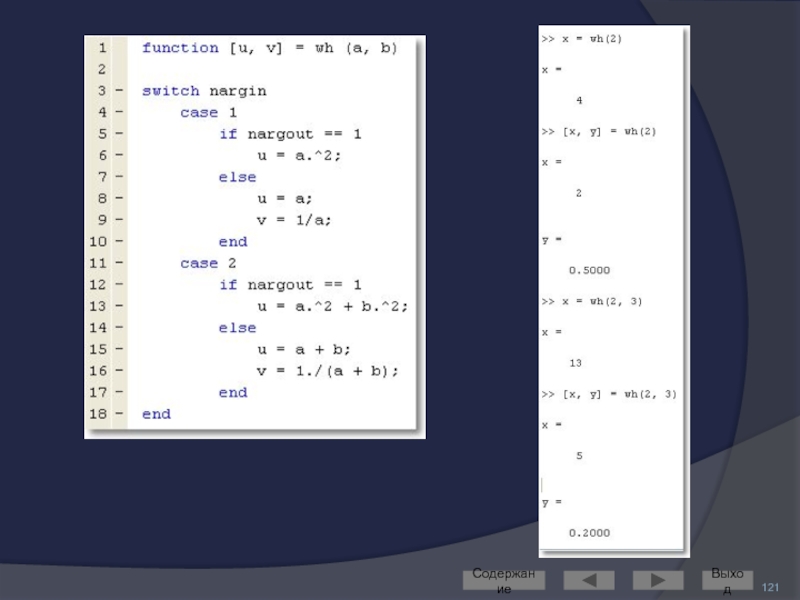
Слайд 120Входные и выходные параметры
При написании функций в Matlab можно проводить проверку
Для этого в описании функции используют служебные слова:
nargin: количество входных параметров
nargout: количество выходных параметров
Содержание
Выход
Слайд 122Подфункции
В файлах-функциях Matlab могут быть реально описаны несколько функций
Синтаксически это оформляется
При вызове такого m-файла происходит запуск самой первой функции
её имя должно совпадать с именем файла
Описание следующих функций локально
обычно они используются как вспомогательные для первой функции
Содержание
Выход
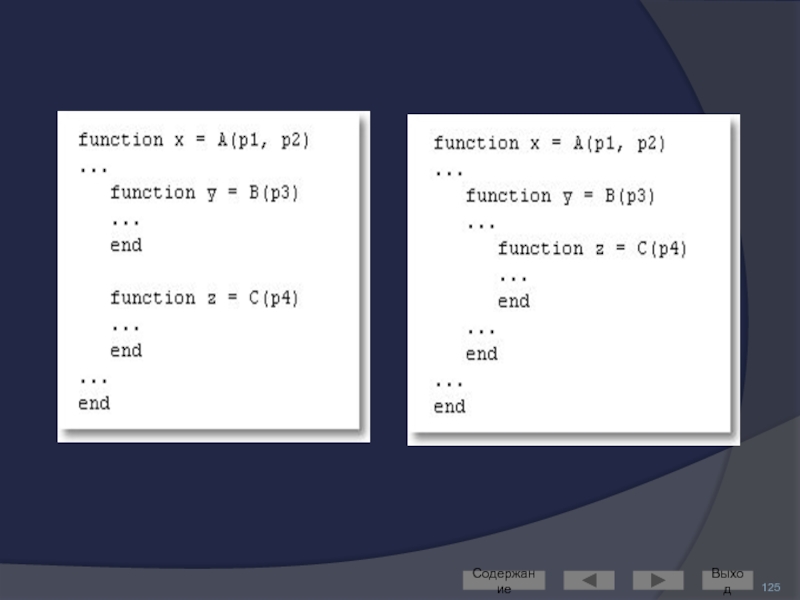
Слайд 124Вложенные функции
Помимо последовательного вложения в один файл функция может быть описана
Такая функция называется вложенной
Вложенная функция, в свою очередь, может содержать другие вложенные функции
Содержание
Выход
Слайд 126Создание p-кода
При вызове m-файла сравнительно много времени тратится на его компиляцию
Чтобы
команда pcode <имя m-файла>
Откомпилированный в псевдокод файл получает расширение «p»
Такой файл будет выполняться быстрее, чем обычный m-файл
Содержание
Выход
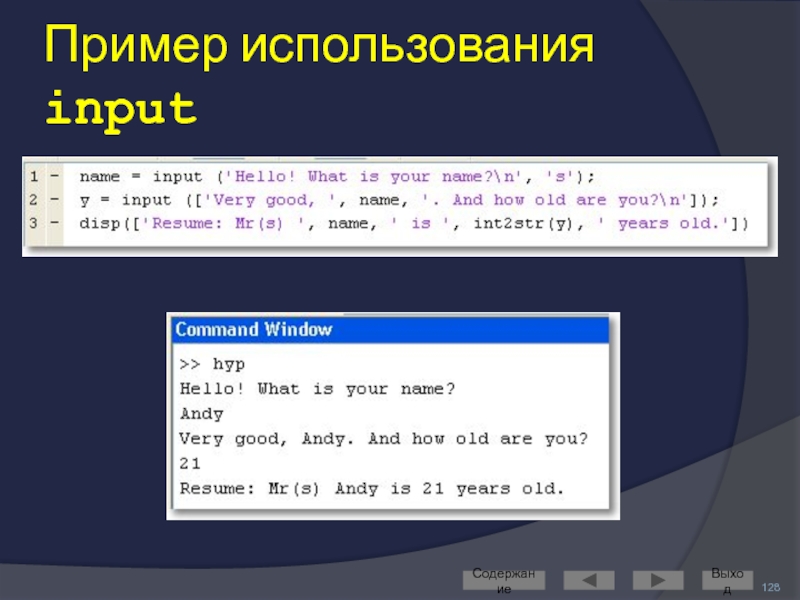
Слайд 127Интерактивный ввод данных
Используется при написании скриптов
Для ввода числовых данных применяют
x = input(’строка приглашения’)
Введённое пользователем значение сохранится в переменной x
Для ввода строковых данных функция input вызывается с дополнительным параметром:
c = input(’строка приглашения’,’s’)
Кроме того, имеется Си-подобная функция sscanf
Содержание
Выход
Слайд 129Вывод данных в командное окно
Для этого используют команду disp (от display)
disp(<выводимая строка>)
Если выводимое значение – число, то вначале его преобразуют к строковому типу при помощи функций int2str или num2str
Конкатенацию строк производят как для одномерных векторов-строк
Кроме того, имеется Си-подобная функция sprintf
Содержание
Выход
Слайд 130Основные языковые конструкции
Как и любой процедурный язык высокого уровня, Matlab позволяет
следование
ветвление
циклы
пользовательские функции
Содержание
Выход
Слайд 131Следование
Реализуется перечислением каждого из операторов в отдельной строке
Либо в одной строке
Содержание
Выход
Слайд 132Ветвление
Реализуется в двух вариантах:
при помощи оператора if
при помощи оператора switch
Содержание
Выход
Слайд 134Полный формат оператора if
В полном варианте оператора могут использоваться слова else
Слово elseif может использоваться в одном операторе многократно с указанием условия
Слово else – только один раз в конце оператора и без условия
Содержание
Выход
Слайд 135Циклы
В Matlab имеется два вида циклов:
цикл с параметром for
цикл c предусловием
Также имеются
оператор досрочного выхода из цикла break
оператор перехода к следующей итерации continue
Содержание
Выход
Слайд 137Замечание по использованию цикла с параметром
Обычно цикл for используется для обработки
Важно помнить, что если есть возможность обойтись без этого цикла (применить матричные или векторные операции), то лучше избавиться от явного цикла
В этом случае программа будет работать на порядок быстрее
Содержание
Выход
Слайд 140Цикл с предусловием
Синтаксис:
while
Операторы выполняются, пока логическое выражение есть истина (true)
Содержание
Выход
Слайд 142Операторы break и continue
Аналогичны одноимённым операторам Паскаля
Break производит досрочный выход из
Continue прекращает выполнение текущей итерации и переходит к следующей
Содержание
Выход
Слайд 143Операторы break и continue
(пример)
Написать скрипт, который вводит с клавиатуры произвольное количество
Содержание
Выход
Слайд 146Вычисления в Matlab
Пример: вычисление определённого интеграла
По формуле Ньютона: F(x)|ab =F(b)
получаем точный результат
но первообразную не всегда можно найти
Численно: методом прямоугольников, трапеций, Симпсона и пр.
можно пользоваться даже тогда, когда интеграл «не берётся»
но при вычислении возникают погрешности
Содержание
Выход
Слайд 147Средства Matlab для символьных вычислений
Изначально Matlab имел средства только для численного
Сегодня в Matlab встроены средства аналитических (символьных) вычислений
Symbolic Math Toolbox
Является вычислительным ядром системы Maple V
Установка Maple не требуется
Содержание
Выход
Слайд 148Создание символьных переменных
Для символьного анализа требуется создать символьные переменные и функции
Символьные
по одной: x=sym(’x’)
так же можно создать целое символьное выражение
несколько сразу: syms x y z
Символьные функции определяются через символьные переменные: f=x^2+y
Для построения символьных функций можно воспользоваться командой ezplot
Представить в стандартной форме – командой pretty
Содержание
Выход
Слайд 151Символьные вычисления
Преобразования математического анализа
дифференцирование,
пределы,
интегрирование,
разложение в ряд Тейлора
Упрощение
Точная арифметика
Линейная алгебра
Решение уравнений и их систем
обычных и дифференциальных
Содержание
Выход
Слайд 172Операции над полиномами
Реализуются при помощи функций
collect
expand
factor
horner
Содержание
Выход
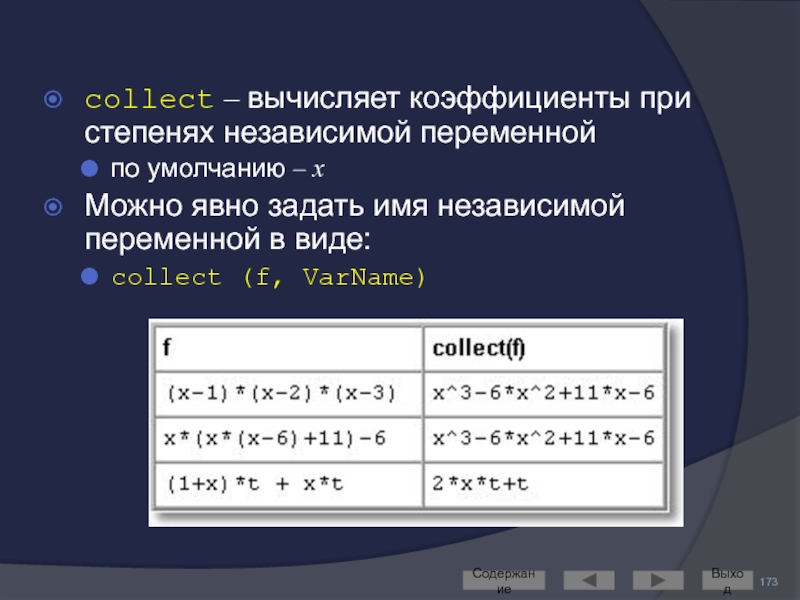
Слайд 173collect – вычисляет коэффициенты при степенях независимой переменной
по умолчанию – x
Можно явно задать имя независимой переменной в виде:
collect (f, VarName)
Содержание
Выход
Слайд 175factor – разлагает полином на множители, если эти множители имеют рациональные
Содержание
Выход
Слайд 178Упрощение выражений
simplify
реализует мощный алгоритм упрощения с использованием тригонометрических, степенных, логарифмических, экспоненциальных
simple
пытается получить выражение, которое представляется меньшим числом символов, чем исходное, последовательно применяя все функции упрощения Symbolic Math Toolbox
Содержание
Выход
Слайд 181Simplify против Simple
Иногда simple даёт более удачное решение, чем simplify:
Содержание
Выход
Слайд 182Simple
simple особенно эффективна при работе с тригонометрическими выражениями
Содержание
Выход
Слайд 183Подстановка
subs подставляет одно символьное выражение в другое
Общий формат:
subs(, , )
Содержание
Выход
Слайд 185Подстановка значения в функцию
Подстановка вместо переменной её числового значения приводит к
Содержание
Выход
Слайд 186Точная арифметика
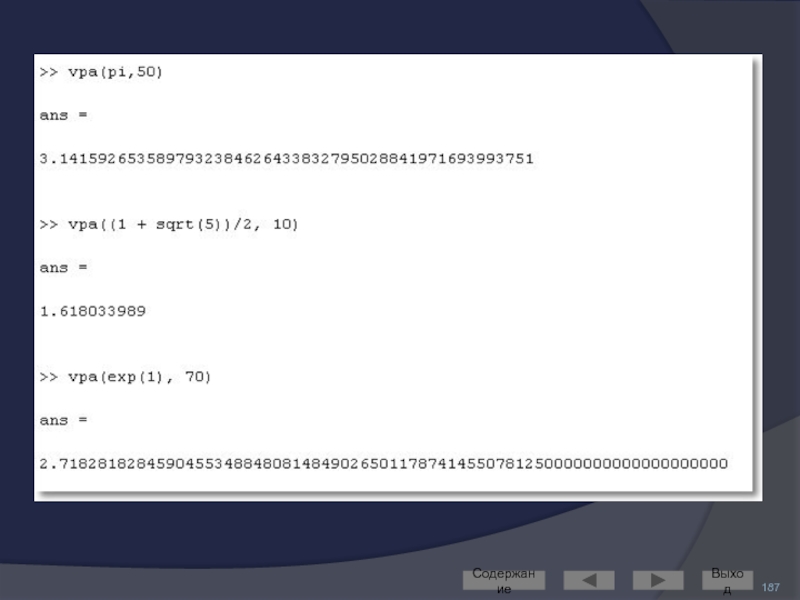
Точные вычисления реализуются функцией vpa (Variable-Precision Arithmetic)
Формат вызова:
vpa(, )
Содержание
Выход
Слайд 188Решение уравнений и систем
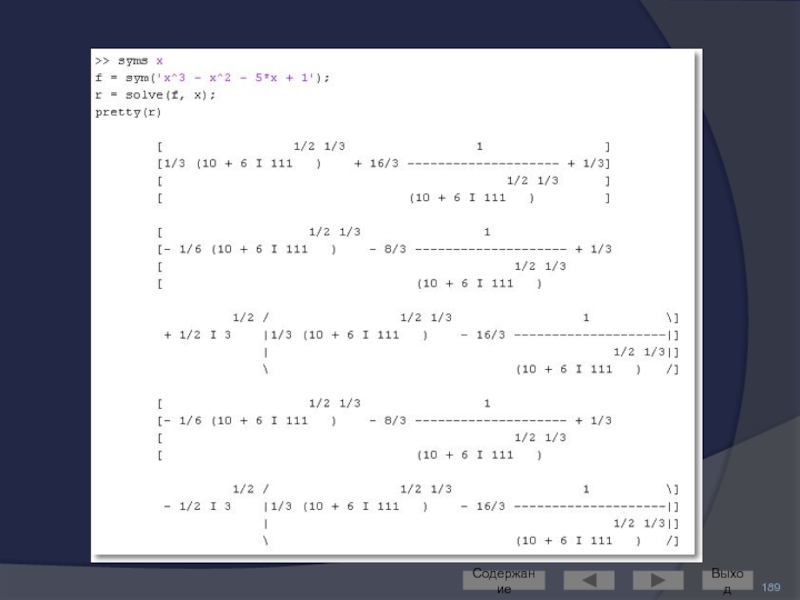
Выполняет команда solve
До 4-го порядка включительно решаются точно
Ответ
Уравнения высших порядков и трансцендентные, как правило, точно не решаются
В этом случае выводится приближённый результат
С целью сокращения записи при выводе могут использоваться подстановки
Содержание
Выход
Слайд 190Решение систем
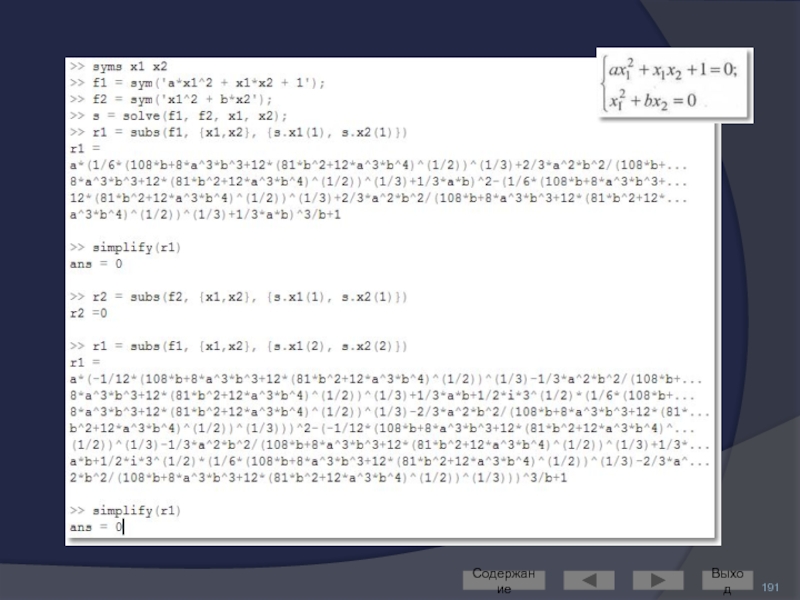
Также выполняет команда solve
Входные аргументы
левые части уравнений
переменные, по которым нужно
например: s = solve(f1, f2, x1, x2)
Выходной аргумент
структура (запись) s с полями (в данном случае) x1 и x2, хранящими символьное представление решения
Содержание
Выход
Слайд 192Решение дифференциальных уравнений
Выполняет команда dsolve
Если неизвестная функция обозначена символьной переменной y,
Содержание
Выход
Слайд 194Представление и преобразование математических моделей (ММ) динамических систем (ДС).
Задание ДС в
В современной теории управления для описания ММ ДС используется запись, представляющая собой систему уравнений в переменных состояния [1]
(1)
Содержание
Выход
Слайд 195Задание ДС во вход-выходной (ВВ) форме записи
В классической теории управления для
(2)
Для ввода ПФ коэффициенты числителя и знаменателя необходимо задавать в виде вектора (в порядке убывания степени).
NUM=[bm bm-1 ... b1 b0]
DEN=[am am-1 ... a1 a0]
Содержание
Выход
Слайд 197Преобразование ПФ:
[NUMc,DENc]=tfchk(NUM,DEN) – проверяет на соответствие порядки числителя и знаменателя,
[Z,P,K]=tf2zp(NUM,DEM) – находит нули, полюсы и коэффициент передачи (приведенный);
[NUM,DEN]=zp2tf(Z,P,K) – обратное преобразование;
[A,B,C,D]=tf2ss(NUM,DEN) – преобразуем ПФ с одним входом в модель ПС в канонической форме управления. Для перехода также все матрицы необходимо развернуть на 1800: A=rot90(A,2), B=rot90(B,2) и т.д.;
abcdchk(A,B,C,D) – проверяет согласованность размерности матриц и в случае ошибки возвращает сообщение о ней;
[Wn,ksi]=damp(A) – вычисляет сопрягающие частоты и коэффициенты затухания ДС (А может быть либо системной матрицей, либо векторами NUM или DEN, либо векторами корней Z или P);
Содержание
Выход
Слайд 198Построение частотных характеристик:
[Mod,Fi]=bode(A,B,C,D,ui,w),
[Mod,Fi]=bode(NUM,DEN,w) – возвращает вектор амплитуды и фазы (ui номер
Построение фазовой частотной характеристики для неминимально-фазовых звеньев выше 1-го порядка с использованием данной функции выполняется неправильно.
Для коррекции фазовой характеристики имеются следующие характеристики:
Fik=fixphase(Fi) или Fik=add360(Fi) – устраняет разрыв фазы от –1800 к 1800. Фаза Fi задается в градусах;
Fik=addtwopi(Fi) – то же для фазы, заданной в радианах.
Содержание
Выход
Слайд 199Вычисление переходных процессов:
Y – вектор переходного процесса, t – вектор изменения
X – вектор состояния (необязательный параметр, может быть опущен)
[Y,X]=impulse(A,B,C,D,ui,t),
Y=impulse(NUM,DEN,t) – весовая функция,
[Y,X]=step(A,B,C,D,ui,t),
Y=step(NUM,DEN,t) – реакция на единичное ступенчатое воздействие,
[Y,X]=lsim(A,B,C,D,U,t,X0),
Y=lsim(NUM,DEN,U,t) – реакция на произвольно заданное вектором U внешним воздействием (X0 – начальное условие).
Содержание
Выход
Слайд 200Анализ управляемости:
Q=ctrb(A,B) – вычисляет матрицу управляемости Q,
[Ab,Bb,Cb,T]=ctrbf(A,B,C,TOL) – выделение полностью управляемого
Индекс nc – неуправляемая часть, с – управляемая.
Выделение неуправляемой части:
nc=length(Ab)-rang(Q); Anc=Ab(1:nc,1:nc).
eig(Anc) - cобственные значения неуправляемой части системы.
Содержание
Выход
Слайд 201Анализ наблюдаемости:
R=obsv(A,C) – вычисляет матрицу наблюдаемости R,
[Ab,Bb,Cb,T]=obsvf(A,B,C,TOL) – выделение полностью наблюдаемого
Индекс no – ненаблюдаемая часть, о – наблюдаемая.
Выделение ненаблюдаемой части:
nо=length(Ab)-rang(R); Ano=Ab(1:no,1:no).
eig(Ano) - cобственные значения ненаблюдаемой части системы.
Содержание
Выход
Слайд 202Построение графиков:
plot(X,Y,S) – построение графика функции Y(X) c заданием типа линии
plot3(X,Y,Z,S) – построение трехмерного графика функции Z(X,Y) c заданием типа линии с помощью S (необязательный параметр);
loglog(X,Y,S) – аналогична предыдущей команде, но для задания логарифмического масштаба по X и Y;
semilogx(X,Y,S) или semilogy(X,Y,S) – строит график в логарифмическом масштабе по оси X или Y соответственно;
subplot(m,n,k) – разбивает окно на m окон по горизонтали и n окон по вертикали, а k – номер окна, в котором будет выводиться текущий график;
Содержание
Выход




























![Одномерные массивыЗадание массива:a = [ -3 4 2];a = [ -3, 4, 2];Диапазоны:b = -3:](/img/tmb/5/402441/2f63589054c3007c1cdda17eb02cf8b8-800x.jpg)
![Двумерные массивыЗадание массива:a = [ 1 2; 3 4; 5 6];Доступ к элементу:СодержаниеВыход](/img/tmb/5/402441/6f53982660def458305878c226d08586-800x.jpg)


































![Axis: управление масштабомКоманда axis([Xmin Xmax Ymin Ymax]) задаёт область построения графиков по осям X и](/img/tmb/5/402441/aa60e85b2569864704f4c79014ac72af-800x.jpg)






































































![Преобразование ПФ: [NUMc,DENc]=tfchk(NUM,DEN) – проверяет на соответствие порядки числителя и знаменателя, возвращает эквивалентную ПФ с](/img/tmb/5/402441/f00f27ee5997d151fb47e8da9a9274d4-800x.jpg)
![Построение частотных характеристик:[Mod,Fi]=bode(A,B,C,D,ui,w),[Mod,Fi]=bode(NUM,DEN,w) – возвращает вектор амплитуды и фазы (ui номер входа в МВ ММ).](/img/tmb/5/402441/887a0da361daa9ca11516f8f35d89116-800x.jpg)

![Анализ управляемости:Q=ctrb(A,B) – вычисляет матрицу управляемости Q,[Ab,Bb,Cb,T]=ctrbf(A,B,C,TOL) – выделение полностью управляемого подпространства, для частично управляемой](/img/tmb/5/402441/103e2e4dff5a5e14ffb6b0c4b1ca7d9a-800x.jpg)
![Анализ наблюдаемости:R=obsv(A,C) – вычисляет матрицу наблюдаемости R,[Ab,Bb,Cb,T]=obsvf(A,B,C,TOL) – выделение полностью наблюдаемого подпространства, для частично наблюдаемой](/img/tmb/5/402441/a7e89441918819ff2243049ac6c70a1e-800x.jpg)






