- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Разработка и анализ алгоритмов презентация
Содержание
- 1. Разработка и анализ алгоритмов
- 3. Кормен Т., Лейзерсон Ч., Ривест Р. «Алгоритмы.
- 4. Анализ вычислительной сложности алгоритмов
- 5. Алгоритм Евклида (III в. до н.э)
- 6. Псевдокод
- 7. Псевдокод 1. Отступ от левого поля указывает на уровень вложенности
- 8. Введение Основная задача теории – анализ алгоритмов
- 9. Ресурсы, расходуемые алгоритмом (вычислительные ресурсы) Вычислительные ресурсы
- 10. Абстрактная модель вычислений Основные положения Алгоритм
- 11. 1. Алгоритм рассматривается как набор операций и
- 12. 2. Каждой операции сопоставляется временная стоимость в
- 13. 3. Время работы алгоритма в целом равно
- 14. Оценка сложности
- 15. Оценка сложности
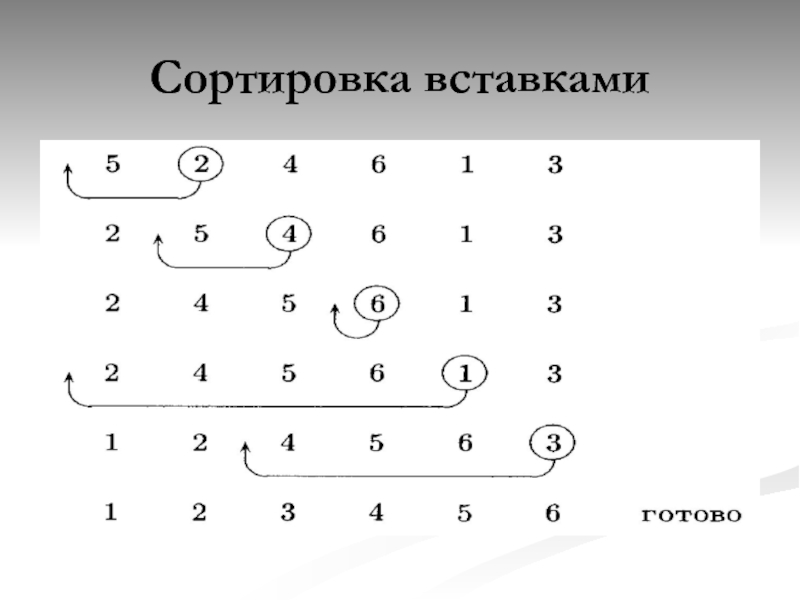
- 16. Сортировка вставками
- 17. Сортировка вставками
- 18. Сортировка вставками
- 19. Худший случай
- 20. Пример анализа вычислительной сложности алгоритма //Алгоритм простого
- 21. Пример анализа вычислительной сложности алгоритма (в упрощенной
- 22. Зависимость от входных данных
- 23. Асимптотический анализ вычислительной сложности алгоритмов Асимптотический
- 24. Асимптотический анализ Основные классы функции «Полиномиальное время»
- 25. Асимптотический анализ Графики основных классов функций
- 26. Асимптотический анализ Область действия ! Асимптотический анализ
- 27. Асимптотический анализ
- 32. Аналогии
- 33. Примеры
- 35. Основные формулы суммирования
- 38. Пример
- 39. Метод итераций
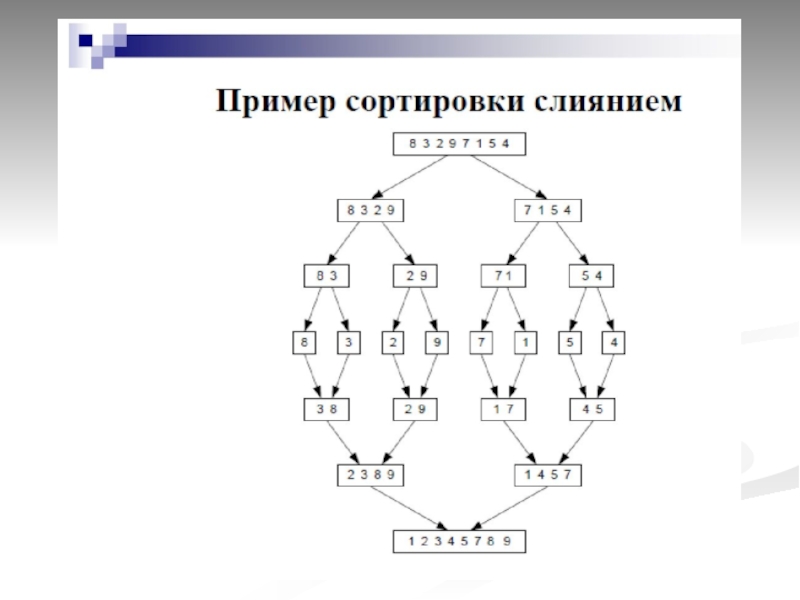
- 42. Сортировка слиянием
- 43. Анализ
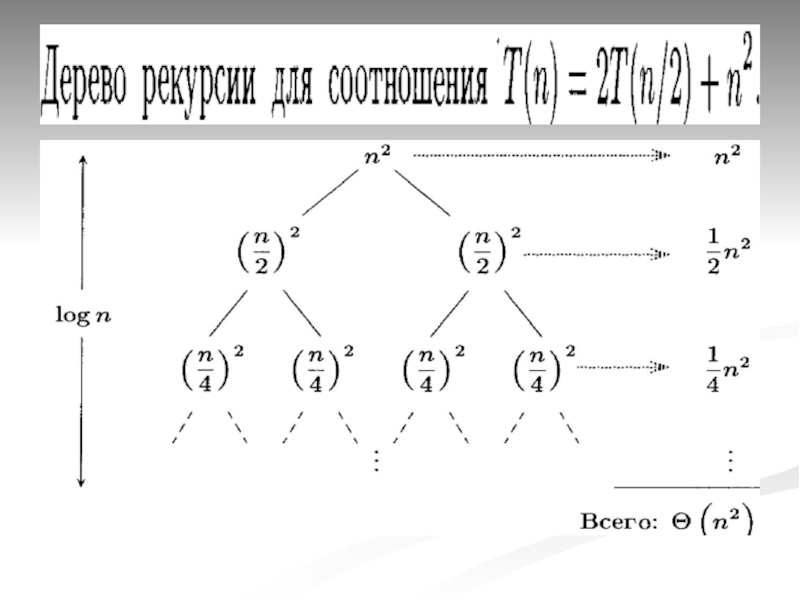
- 45. Основная теорема
Слайд 3Кормен Т., Лейзерсон Ч., Ривест Р.
«Алгоритмы. Построение и анализ»
Левитин А. «Алгоритмы. Введение в разработку и анализ»
(глава 2)
Ахо А., Хопкрофт Дж., Ульман Дж. «Построение и анализ вычислительных алгоритмов»
(глава 1)
Майкл Ласло «Вычислительная геометрия и компьютерная графика на C++»
(глава 2)
Литература по теме
Слайд 8Введение
Основная задача теории – анализ алгоритмов с целями:
определения необходимых объемов ресурсов
сравнения нескольких алгоритмов и выбора более эффективного.
Сложность вычислений (вычислительная сложность алгоритма) = прожорливость алгоритма до ресурсов.
Теория сложности вычислений (вычислительной сложности алгоритма) – раздел теории вычислений, изучающий стоимость работы, требуемой для решения вычислительной задачи.
Слайд 9Ресурсы, расходуемые алгоритмом (вычислительные ресурсы)
Вычислительные ресурсы – возможности, обеспечиваемые компонентами вычислительной
Виды вычислительных ресурсов:
Машинное (однопроцессорное) время (Т) – время работы алгоритма для решения задачи.
Оперативная память (М) – объем памяти с произвольным доступом, необходимый алгоритму для решения поставленной задачи.
Долговременная память – место на жёстком диске.
Пропускная способность сети (трафик).
Энергия поглощаемая и выделяемая.
другие…
Часто удается сокращать объем потребления одного вида ресурса за счет увеличения потребления другого.
Слайд 10Абстрактная модель вычислений
Основные положения
Алгоритм рассматривается как набор операций и управляющих
Каждому виду операций сопоставляется временная стоимость в абстрактных единицах времени (шагах).
Время работы алгоритма в целом равно сумме стоимостей составляющих его операций с учетом вложенности управляющих структур.
Слайд 111. Алгоритм рассматривается
как набор операций и управляющих структур
Базовые виды управляющих
Составной оператор (begin end)
Условие (if then else, case)
Цикл (for, while, repeat)
Основные виды операций
Логические (not, and, or, xor…)
Арифметические (+, -, *, /, div, mod)
Математические функции (sin, cos, log, exp, power..)
Вызов процедур и функций
и др.
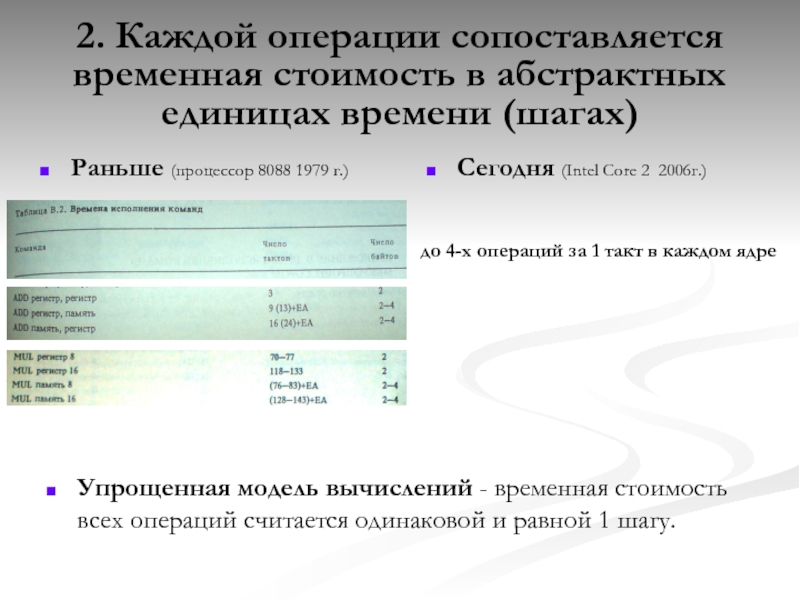
Слайд 122. Каждой операции сопоставляется временная стоимость в абстрактных единицах времени (шагах)
Упрощенная
Раньше (процессор 8088 1979 г.)
Сегодня (Intel Core 2 2006г.)
до 4-х операций за 1 такт в каждом ядре
Слайд 133. Время работы алгоритма в целом равно сумме стоимостей составляющих его
Слайд 20Пример анализа вычислительной сложности алгоритма
//Алгоритм простого последовательного поиска целого числа x
function Search(A: array[1..n] of integer; x: integer): integer;
var i: integer;
begin
//В цикле обход элементов массива
for i := 1 to n do
//Если текущий элемент равен искомому
if A[i] = x then
begin
//то вернуть индекс элемента
result := i;
//и выйти из процедуры
exit;
end;
//вернуть признак того, что элемент не найден
result := -1;
end;
Слайд 21Пример анализа вычислительной сложности алгоритма
(в упрощенной модели вычислений)
//Алгоритм простого последовательного поиска
function Search(A: array[1..n] of integer; x: integer): integer;
var i: integer;
begin //УС1
//В цикле обход элементов массива
for i := 1 to n do //УС2
//Если текущий элемент равен искомому
if A[i] = x then //УС3
begin //УС4
//то вернуть индекс элемента
result := i;
//и выйти из процедуры
exit;
end;
//вернуть признак того, что элемент не найден
result := -1;
end;
Вычислительная сложность управляющих структур алгоритма:
Слайд 22Зависимость от входных данных
Временная сложность поиска числа в массиве зависит
Для упрощения принимается правило: временную сложность алгоритма выражать, как функцию только размера входных данных, НЕ зависящую от содержимого входных данных.
Размер входных данных (N) – величина, характеризующая количество входной информации. (зависит от задачи)
Упростить функцию до TSearch(n) можно несколькими способами:
Наилучший случай – искомое число в первой ячейке TSearch(n)=3
Наихудший случай – искомое число в последней ячейке TSearch(n)=n+2
Средний случай – при равномерной распределении TSearch(n)=(3+(n+2))/2
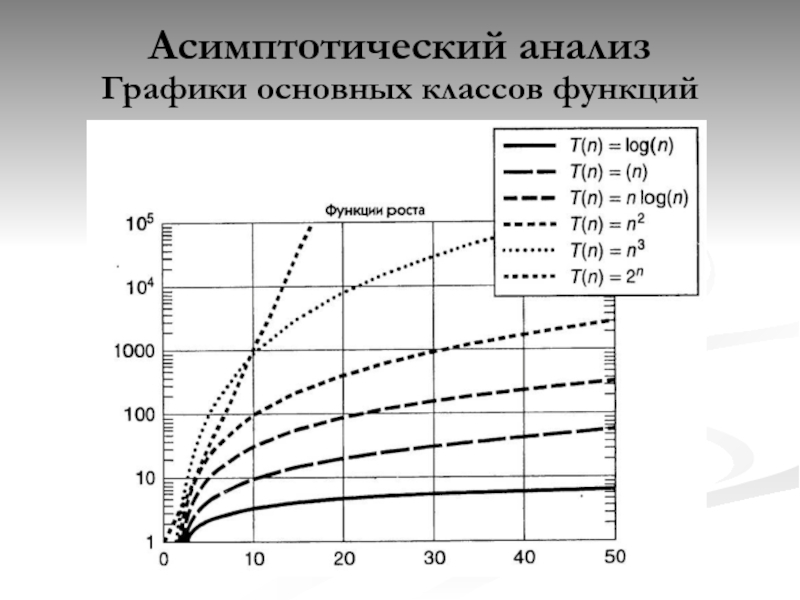
Слайд 23Асимптотический анализ
вычислительной сложности алгоритмов
Асимптотический анализ – анализ поведения функции временной
Асимптотический анализ позволяет оценивать и сравнивать скорость роста функции временной сложности, а так же классифицировать алгоритмы.
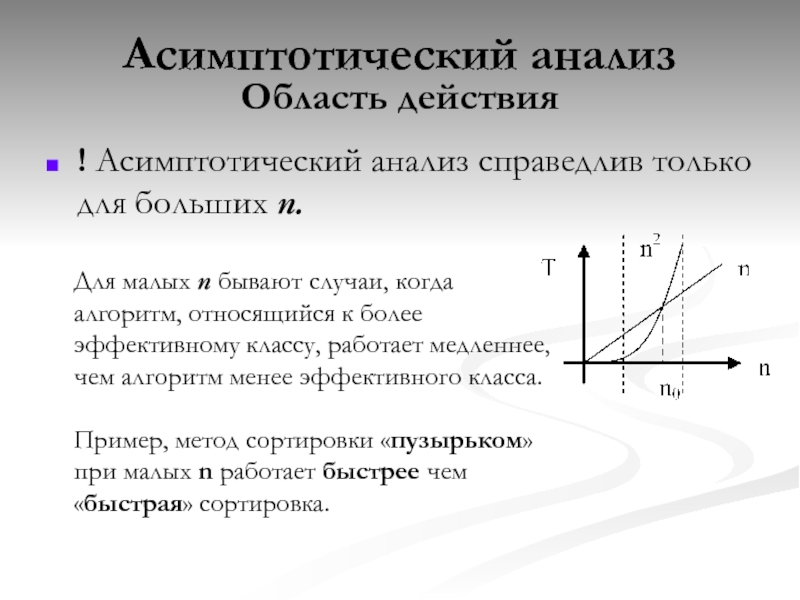
Слайд 26Асимптотический анализ
Область действия
! Асимптотический анализ справедлив только для больших n.
Для малых
Пример, метод сортировки «пузырьком» при малых n работает быстрее чем «быстрая» сортировка.