- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорема синусов презентация
Содержание
- 1. Теорема синусов
- 2. Докажите, что площадь параллелограмма равна произведению
- 3. Докажите, что площадь параллелограмма равна половине
- 4. A D B C = =
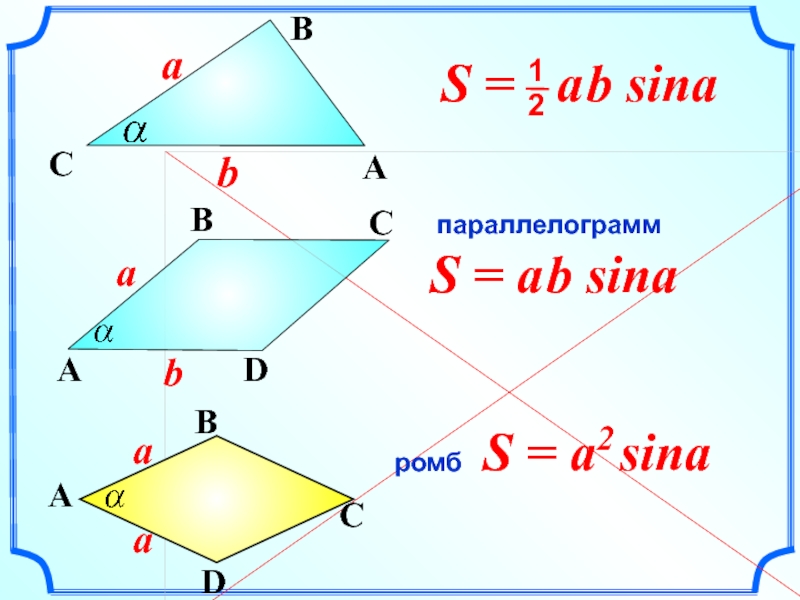
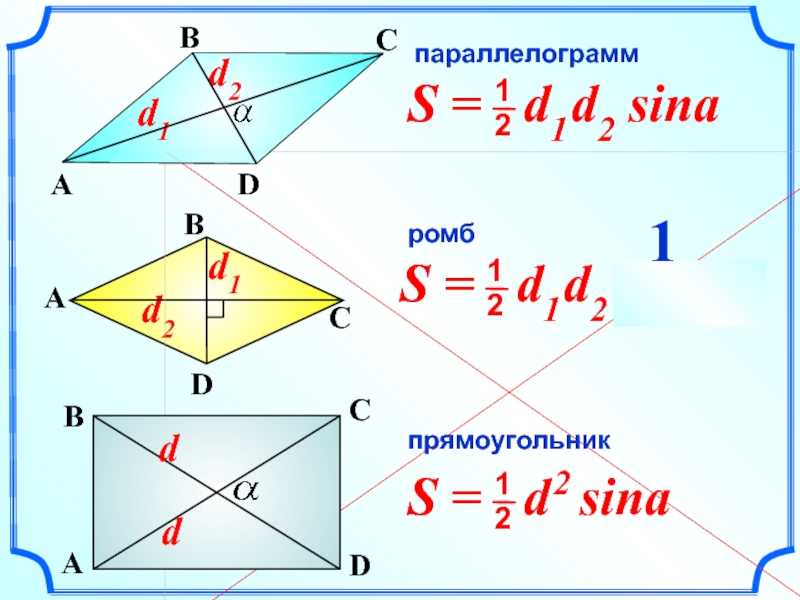
- 5. S = a2 sina параллелограмм ромб S = a b sina
- 6. параллелограмм ромб прямоугольник 1
- 8. C В A
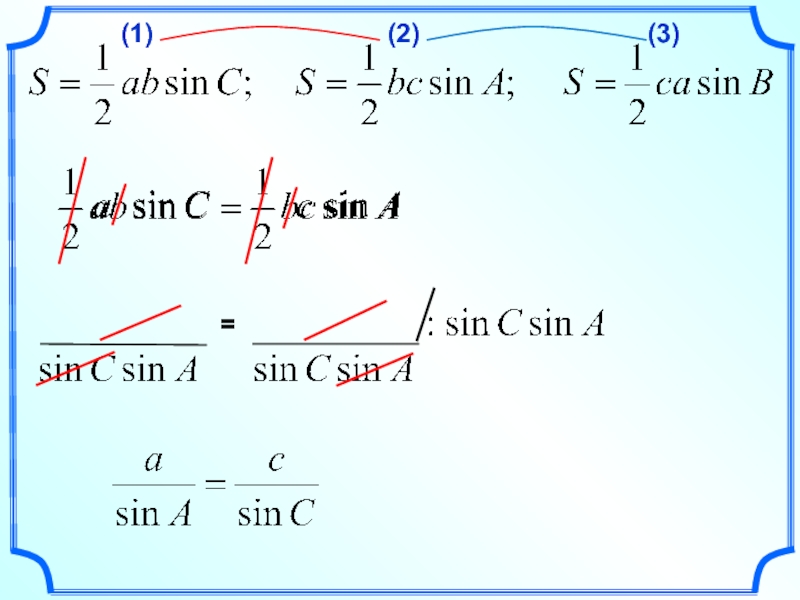
- 9. (1) (2) (3) =
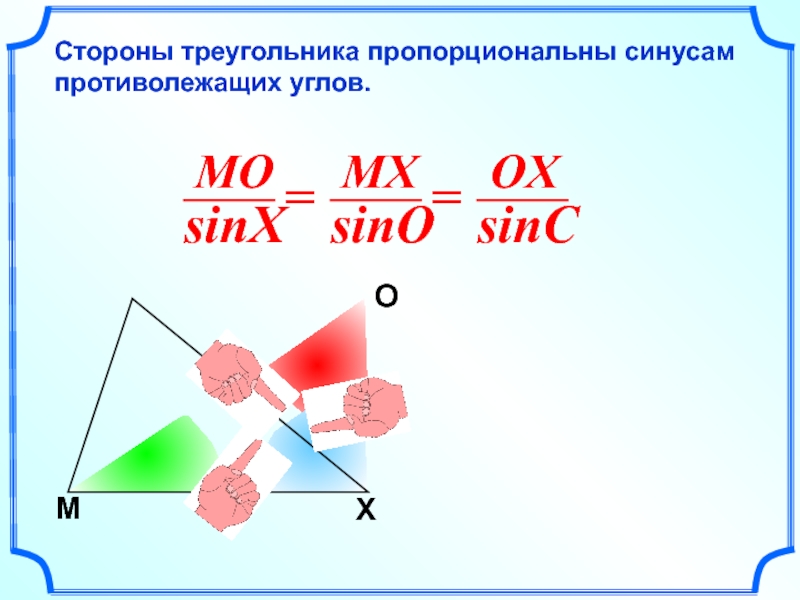
- 10. М O X
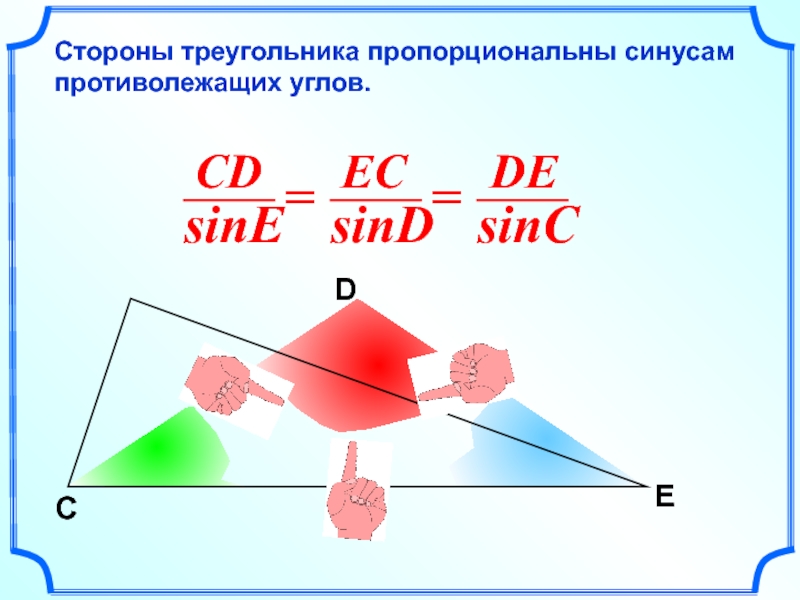
- 11. C D E
- 13. 2
- 16. 1200
- 17. 450 2 450
- 18. a2 = B a A
- 19. (cos2A + sin2A) + c2 – 2bc
- 20. (cos2A + sin2A) + c2 – 2bc
- 21. AB2 = Квадрат стороны треугольника
- 22. XR2 = Квадрат стороны треугольника равен
- 23. Запишите для данного
- 24. На практике удобно сравнивать квадрат большей стороны и сумму квадратов двух других.
- 25. Определите вид треугольника со сторонами 5, 6
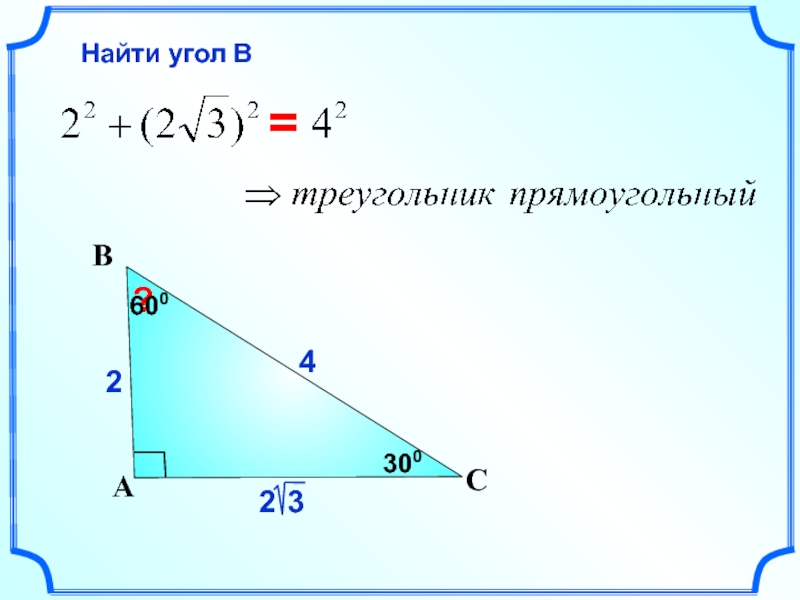
- 26. 4 С А В ? Найти угол В 2 = 300 600
- 27. 4 4 5 AB2 = Квадрат
- 28. 6 6 6 6 6 ВС2 =
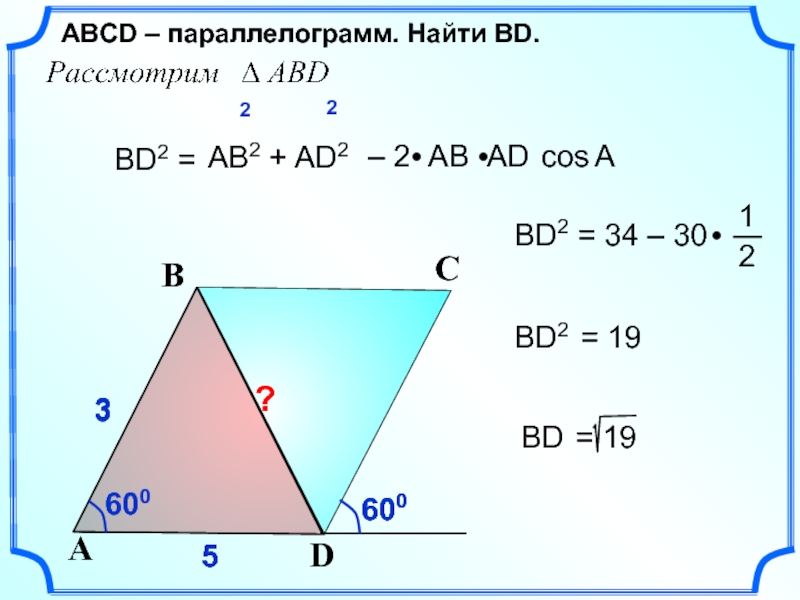
- 29. 600 5 5 3 3
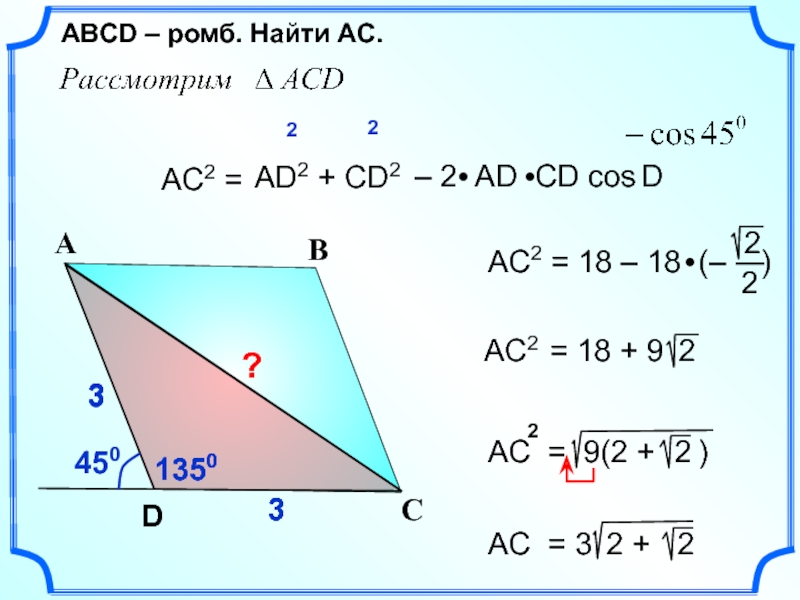
- 30. 3 3 3 1350 1350
Слайд 2
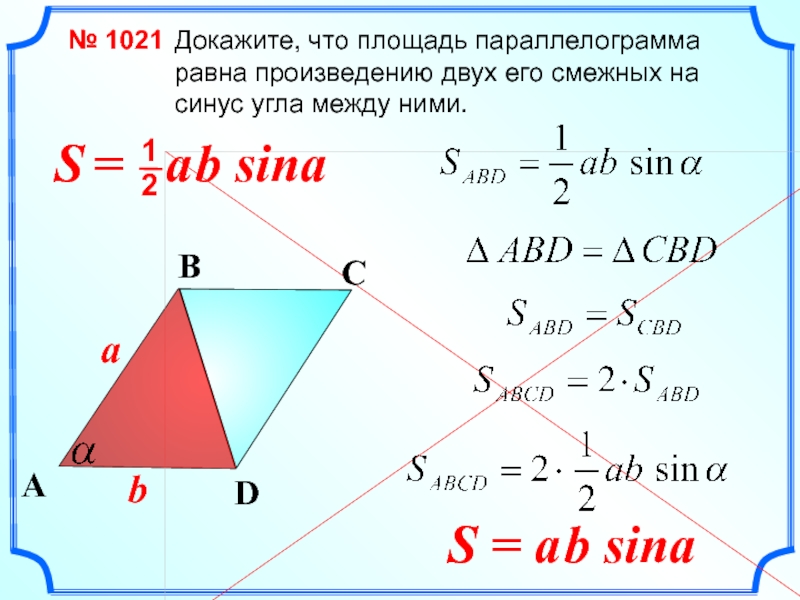
Докажите, что площадь параллелограмма равна произведению двух его смежных на синус
A
a
D
B
S = a b sina
№ 1021
b
C
Слайд 3
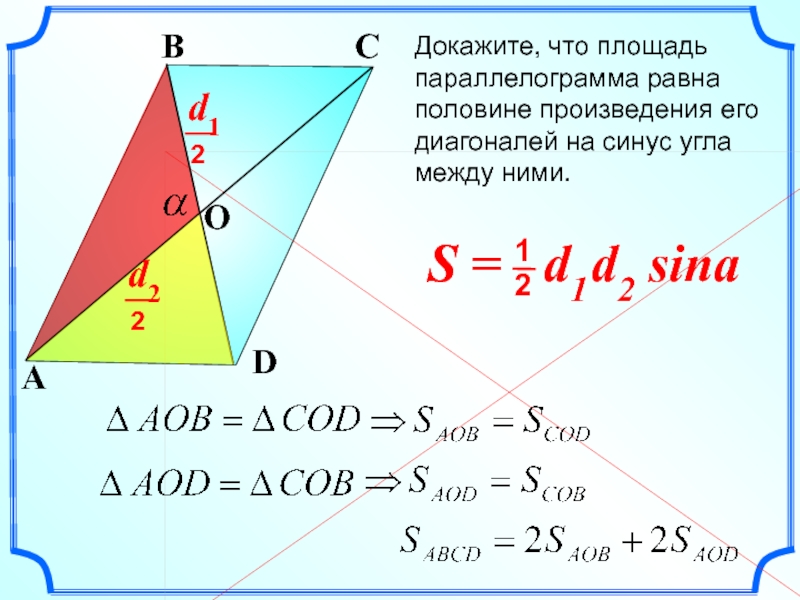
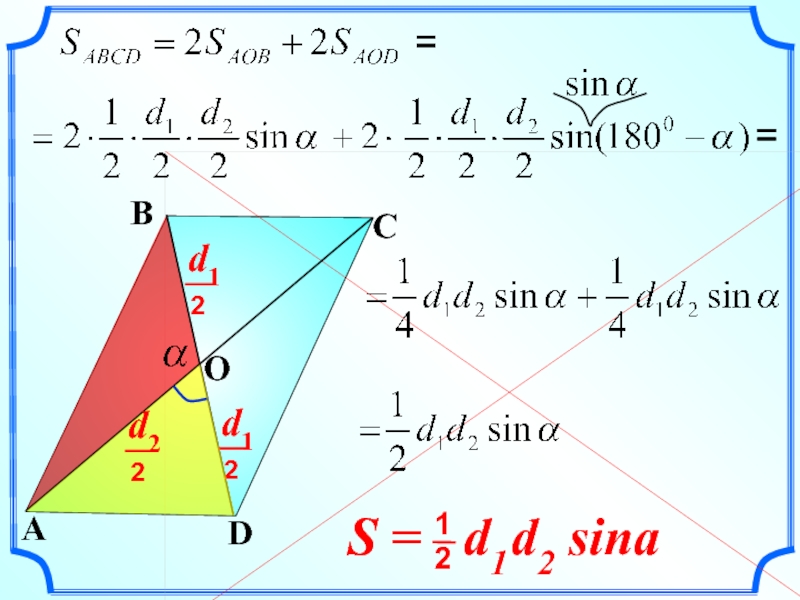
Докажите, что площадь параллелограмма равна половине произведения его диагоналей на синус
A
D
B
C
Слайд 12
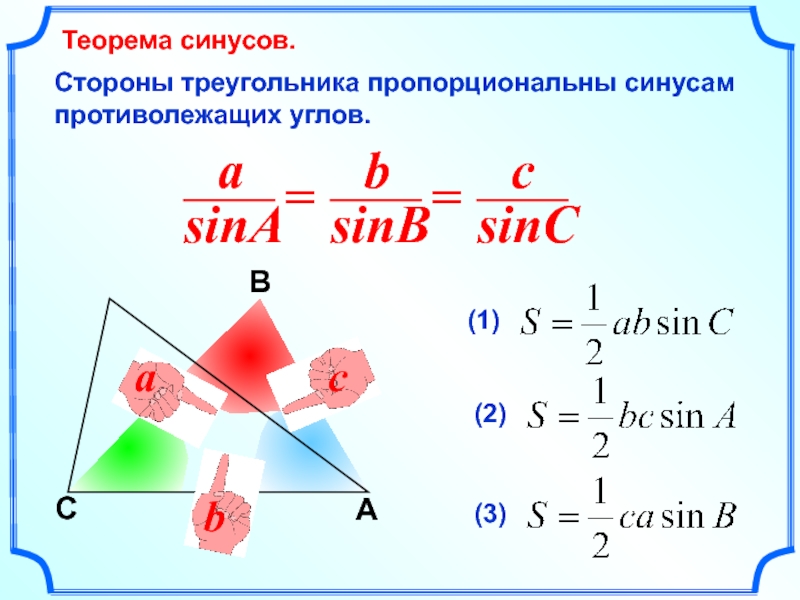
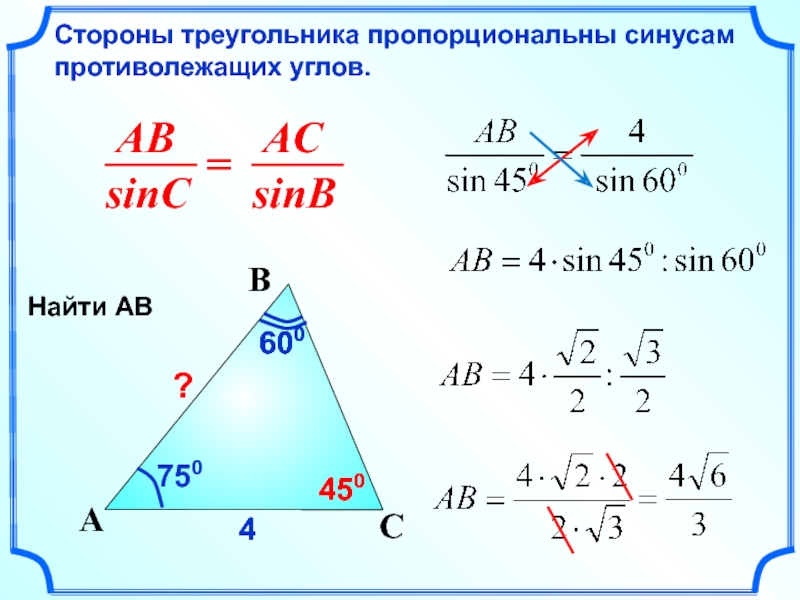
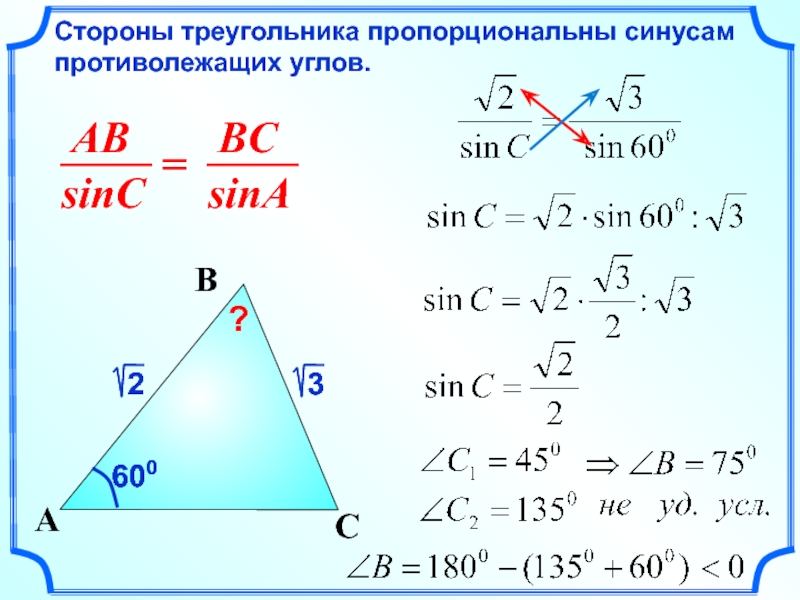
Стороны треугольника пропорциональны синусам противолежащих углов.
C
A
B
750
600
600
4
4
?
450
450
Найти
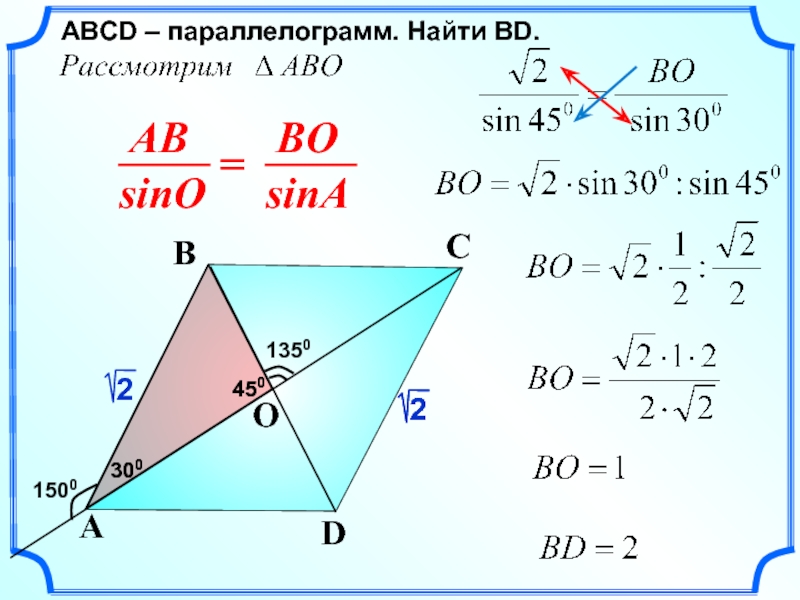
Слайд 132
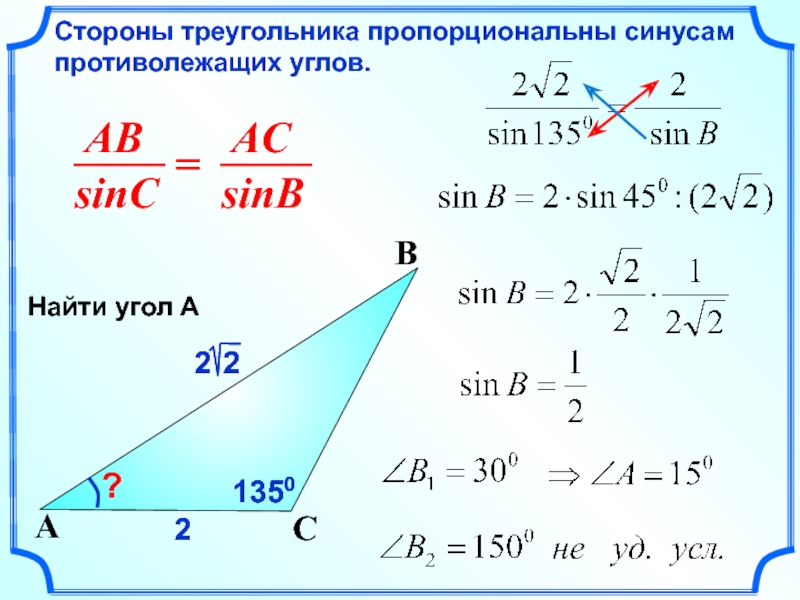
Стороны треугольника пропорциональны синусам противолежащих углов.
C
A
B
?
2
1350
1350
Найти
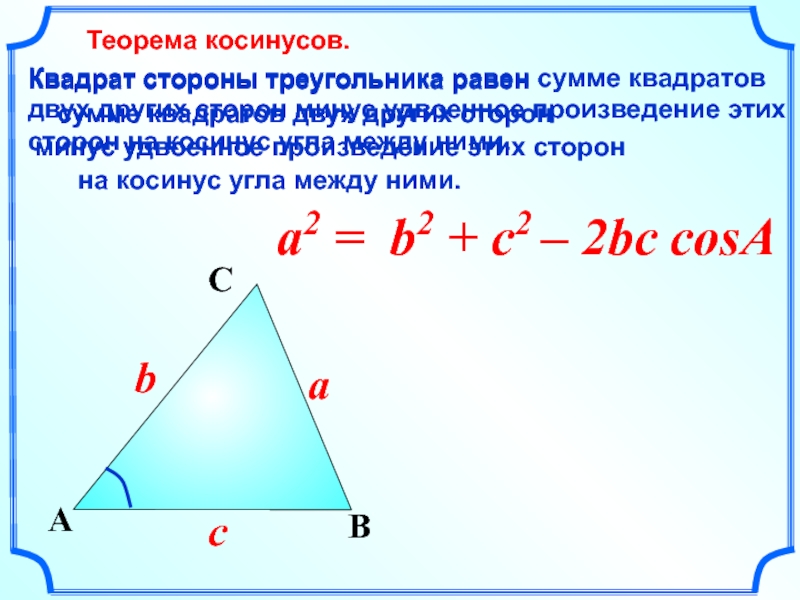
Слайд 18a2 =
B
a
A
C
c
b
Квадрат стороны треугольника равен сумме квадратов двух других сторон
Квадрат стороны треугольника равен
сумме квадратов двух других сторон
на косинус угла между ними.
минус удвоенное произведение этих сторон
b2 + c2
– 2bc
cosA
Теорема косинусов.
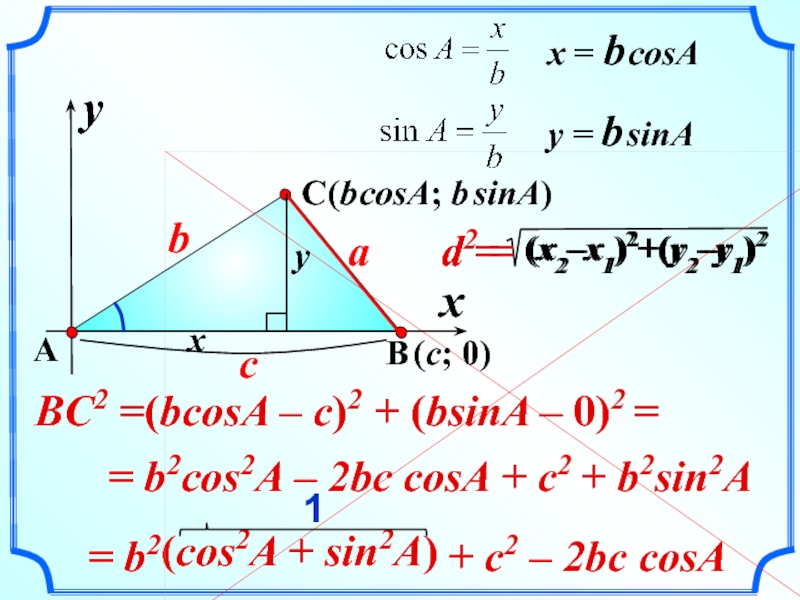
Слайд 19(cos2A + sin2A)
+ c2 – 2bc cosA
A
b
B
C
x = b cosA
y =
c
a
(c; 0)
(b cosA; b sinA)
BC2 =(bcosA – c)2
– 2bc cosA
+ b2sin2A
= b2cos2A
+ c2
= b2
+ (bsinA – 0)2 =
x
y
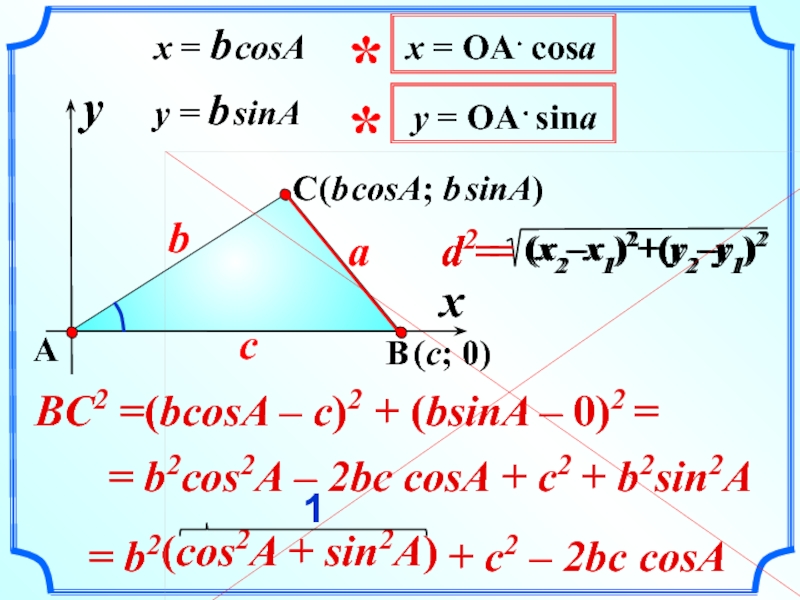
Слайд 20(cos2A + sin2A)
+ c2 – 2bc cosA
A
b
B
C
x = b cosA
y =
c
a
(c; 0)
(b cosA; b sinA)
BC2 =(bcosA – c)2
– 2bc cosA
+ b2sin2A
= b2cos2A
+ c2
= b2
+ (bsinA – 0)2 =
Слайд 21AB2 =
Квадрат стороны треугольника равен сумме квадратов двух других сторон
Квадрат стороны треугольника равен
сумме квадратов двух других сторон
на косинус угла между ними.
минус удвоенное произведение этих сторон
BC2 + CA2
cos
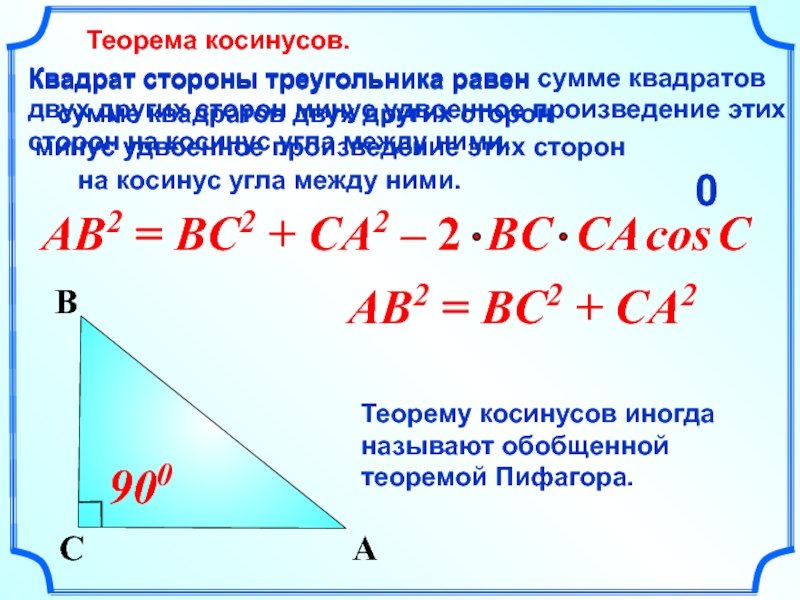
Теорема косинусов.
900
C
0
AB2 = BC2 + CA2
Теорему косинусов иногда называют обобщенной теоремой Пифагора.
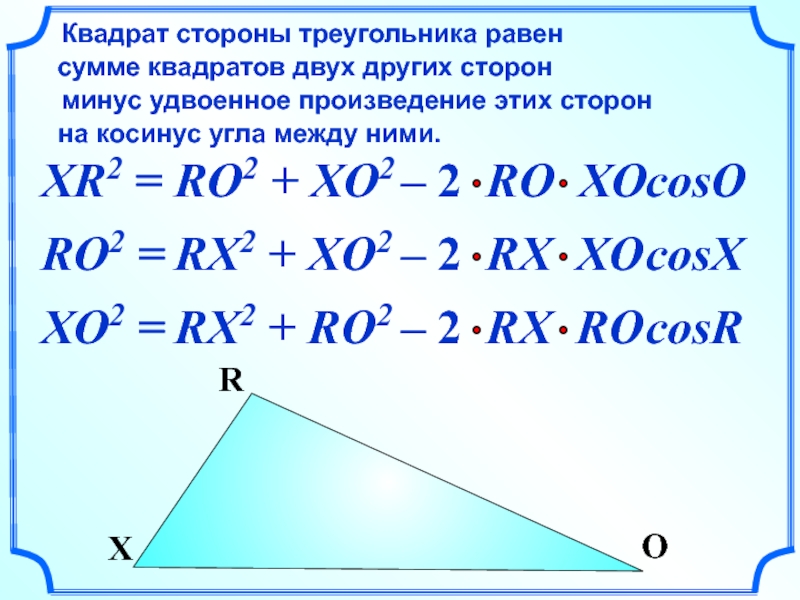
Слайд 22XR2 =
Квадрат стороны треугольника равен
сумме квадратов двух
на косинус угла между ними.
минус удвоенное произведение этих сторон
RO2 + XO2
cosO
RO2 =
RX2 + XO2
cosX
XO2 =
RX2 + RO2
cosR
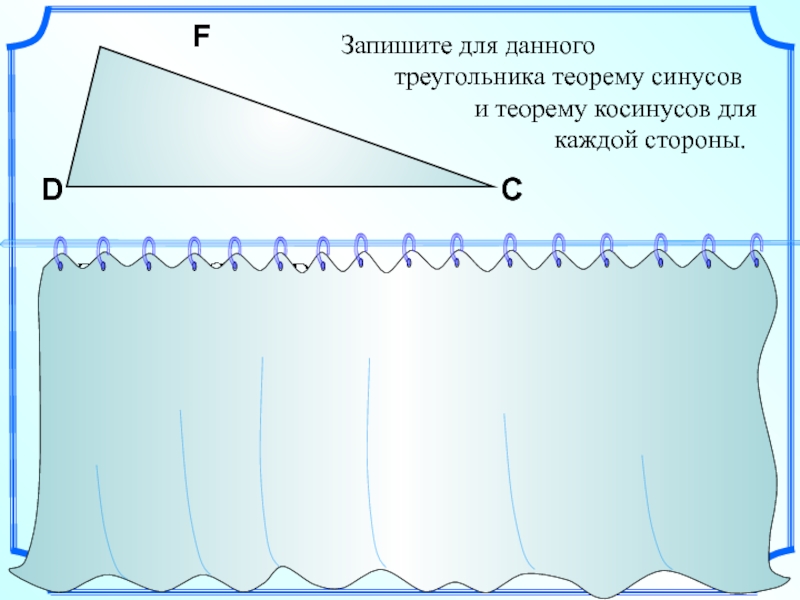
Слайд 23Запишите для данного
треугольника теорему синусов
каждой стороны.
F
D
С
Слайд 25Определите вид треугольника со сторонами 5, 6 и 7 см.
>
Определите
>
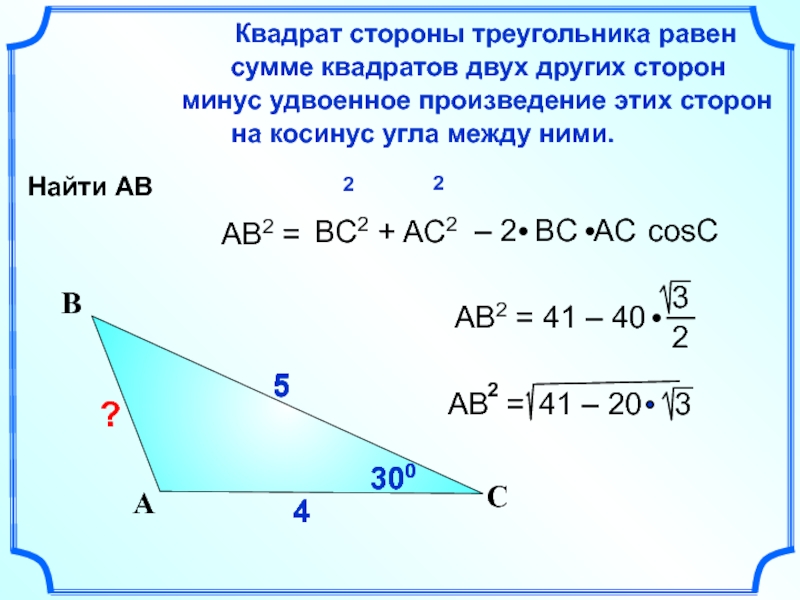
Слайд 274
4
5
AB2 =
Квадрат стороны треугольника равен
сумме квадратов двух
на косинус угла между ними.
минус удвоенное произведение этих сторон
BC2 + AC2
cosC
С
А
В
5
AB = 41 – 20
2
2
5
300
300
2
?
4
Найти АВ
Слайд 286
6
6
6
6
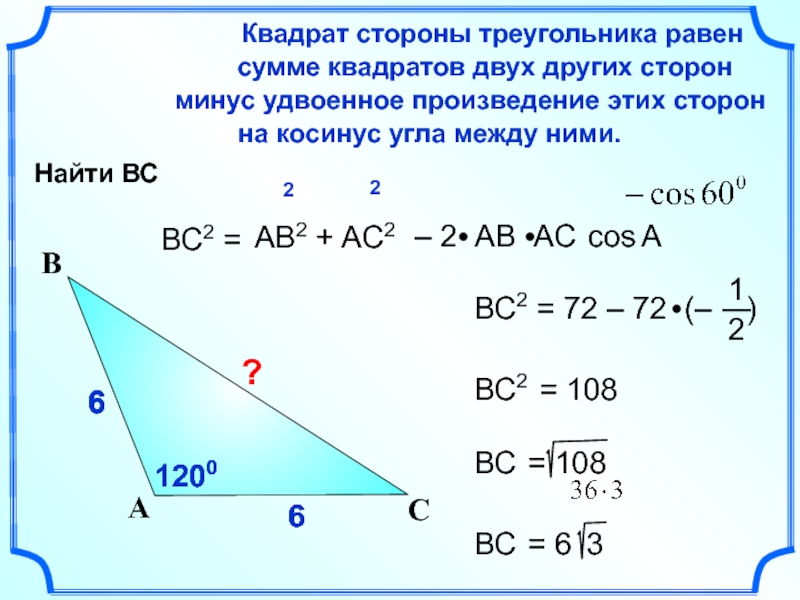
ВС2 =
Квадрат стороны треугольника равен
сумме квадратов двух
на косинус угла между ними.
минус удвоенное произведение этих сторон
АВ2 + AC2
cos
С
А
В
ВС2 = 108
2
2
?
6
А
1200
1200
Найти ВС