- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Угол между плоскостями. (Урок 3. Решаем С2 ЕГЭ. 11класс) презентация
Содержание
- 1. Угол между плоскостями. (Урок 3. Решаем С2 ЕГЭ. 11класс)
- 2. Цели: Повторить понятие угла между плоскостями, нормали
- 3. 1. Основание
- 4. (0; 5; 0)
- 5. Теперь найдем тангенс.
- 6. 2. В
- 7. 12
- 8. 3. Основание
- 9. D1
- 11. 4. В прямоугольном параллелепипеде
- 12. C C1 B1 D B
- 14. 7. В правильной
- 16. Домашнее задание 1. Основание прямой четырехугольной призмы
Слайд 1Тема: Угол между плоскостями. Урок 3
«Решаем С2 ЕГЭ»
Разработала: Куракова Е.
МБОУ СОШ с УИОП №38
им.Е.А. Болховитинова
11 класс физико-математического профиля
Слайд 2Цели:
Повторить понятие угла между плоскостями, нормали к плоскости.
Закрепить методы введение координат
Рассмотреть
Блитц-опрос по терминам
Слайд 3
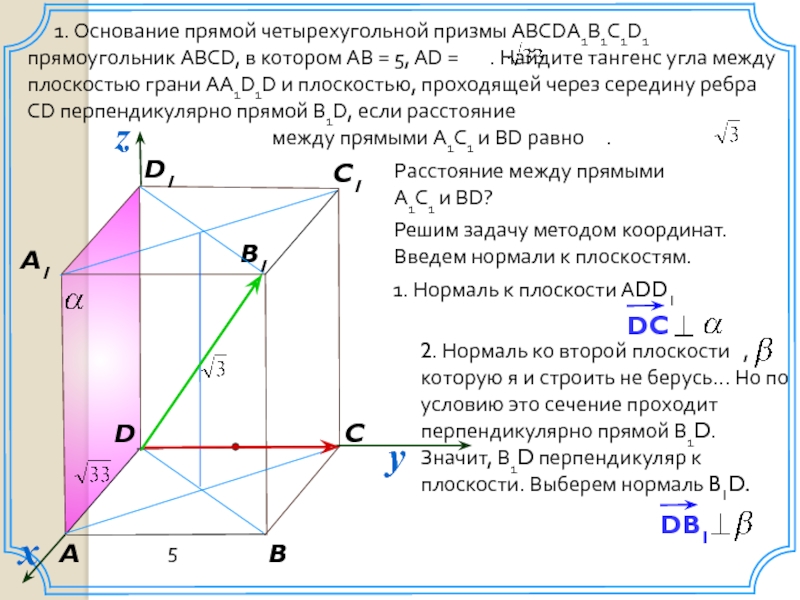
1. Основание прямой четырехугольной призмы ABCDA1B1C1D1 прямоугольник ABCD,
между прямыми A1C1 и BD равно .
D1
B
A
D
B1
C1
A1
5
Расстояние между прямыми
A1C1 и BD?
C
Решим задачу методом координат. Введем нормали к плоскостям.
y
Слайд 4(0; 5; 0)
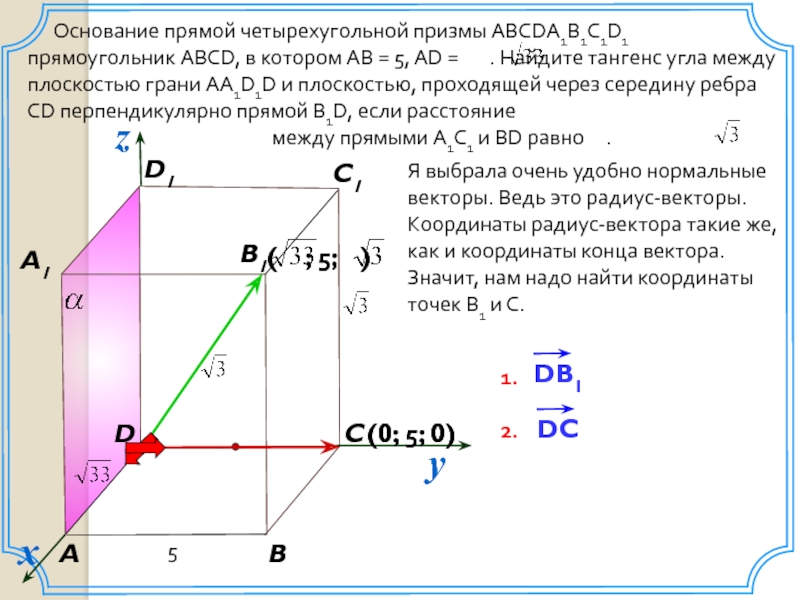
Основание прямой четырехугольной призмы ABCDA1B1C1D1 прямоугольник
между прямыми A1C1 и BD равно .
D1
B
A
D
B1
C1
A1
5
Я выбрала очень удобно нормальные векторы. Ведь это радиус-векторы. Координаты радиус-вектора такие же, как и координаты конца вектора. Значит, нам надо найти координаты точек В1 и С.
C
y
(0; 5; 0)
Слайд 6
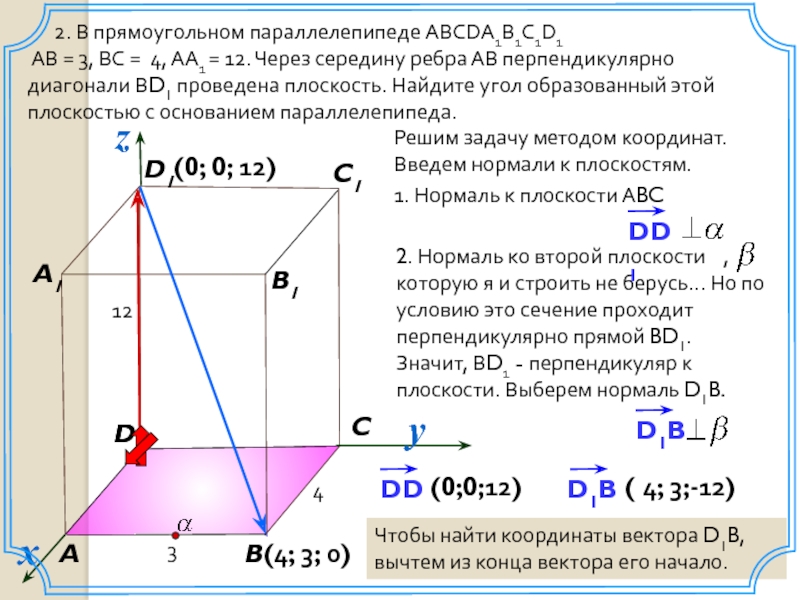
2. В прямоугольном параллелепипеде ABCDA1B1C1D1
AB
D1
B
A
D
B1
C1
A1
3
C
Решим задачу методом координат. Введем нормали к плоскостям.
y
4
12
D
(0; 0; 12)
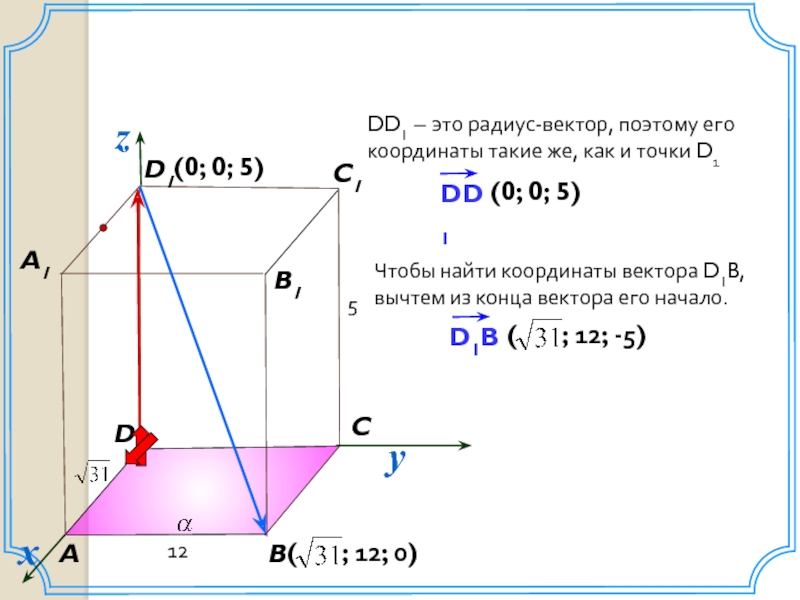
DD1 – это радиус-вектор, поэтому его координаты такие же, как и точки D1
(4; 3; 0)
Чтобы найти координаты вектора D1B, вычтем из конца вектора его начало.
Слайд 8
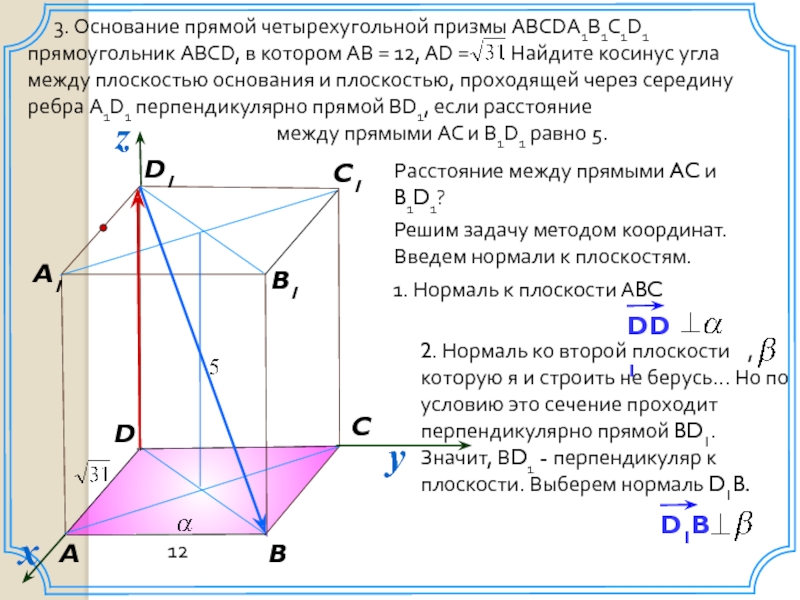
3. Основание прямой четырехугольной призмы ABCDA1B1C1D1 прямоугольник ABCD,
между прямыми AC и B1D1 равно 5.
D1
B
A
D
B1
C1
A1
12
Расстояние между прямыми AC и
B1D1?
C
Решим задачу методом координат. Введем нормали к плоскостям.
y
Слайд 11 4. В прямоугольном параллелепипеде ABCDA1B1C1D1 известны ребра:, AB
C
C1
B1
D
B
D1
A
A1
12
5
(12;0;0)
В данной задаче построение линейного угла не столь очевидно.
Поэтому применим метод координат.
Найдем вектор нормали плоскости AD1B1. Рассмотрим два вектора этой плоскости:
(0;0;5)
(0;5;0)
(12;5;5)
Получим систему
Вектор нормали плоскости AD1B1:
Слайд 12C
C1
B1
D
B
D1
A
A1
5
12
5
(12;0;0)
Найдем вектор нормали плоскости CD1B1. Рассмотрим два вектора этой плоскости:
(0;0;5)
5
(0;5;0)
(12;5;5)
Получим систему
Вектор
Слайд 14
7. В правильной четырехугольной призме ABCDA1B1C1D1 диагональ основания
C
C1
B1
D
B
D1
A
A1
1
В данной задаче построение линейного угла не столь очевидно. Поэтому применим метод координат.
Найдем вектор нормали плоскости АCB1. Рассмотрим два вектора этой плоскости:
Получим систему
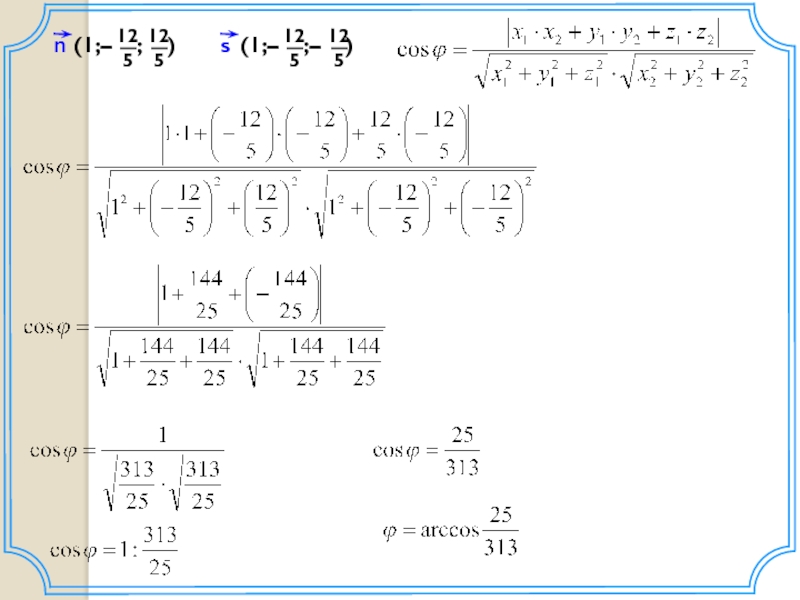
Вектор нормали плоскости ACB1:
Вектор нормали плоскости ВВ1С1:
Слайд 16Домашнее задание
1. Основание прямой четырехугольной призмы ABCDA1B1C1D1 прямоугольник ABCD, в котором
2. В прямоугольном параллелепипеде ABCDA1B1C1D1 AB = 3, ВС = 4, АА1 = 12. Через середину ребра АВ перпендикулярно диагонали ВD1 проведена плоскость. Найдите угол образованный этой плоскостью боковыми плоскостями параллелепипеда.
3. Основание прямой четырехугольной призмы ABCDA1B1C1D1 прямоугольник ABCD, в котором AB = 12, AD = . Найдите косинус угла между плоскостью основания и плоскостью, проходящей через середину ребра A1D1 перпендикулярно прямой B1D, если расстояние между прямыми AC и B1D1 равно 5.
4. В прямоугольном параллелепипеде ABCDA1B1C1D1 известны ребра: AB = 5, AD = 12, СС1 = 5. Найдите угол между плоскостями CD1B1и AD1B1.
5. В правильной четырехугольной призме ABCDA1B1C1D1 диагональ основания в 2 раза больше бокового ребра. Найдите угол между плоскостью DCB1и боковой гранью ВВ1С1С.