- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математика и искусство презентация
Содержание
- 1. Математика и искусство
- 2. Математика - царица всех наук,
- 3. Искусство - творческое отражение, воспроизведение
- 4. Математика владеет не только истиной,
- 5. К фундаментальным понятиям симметрии относятся
- 6. Общие
- 7. Многогранник - это трехмерное тело,
- 8. Платоновы тела Архимедово тело М.
- 9. Тесселляции, известные также как покрытие
- 10. Роберт Фатауэр "Фрактальные рыбы -
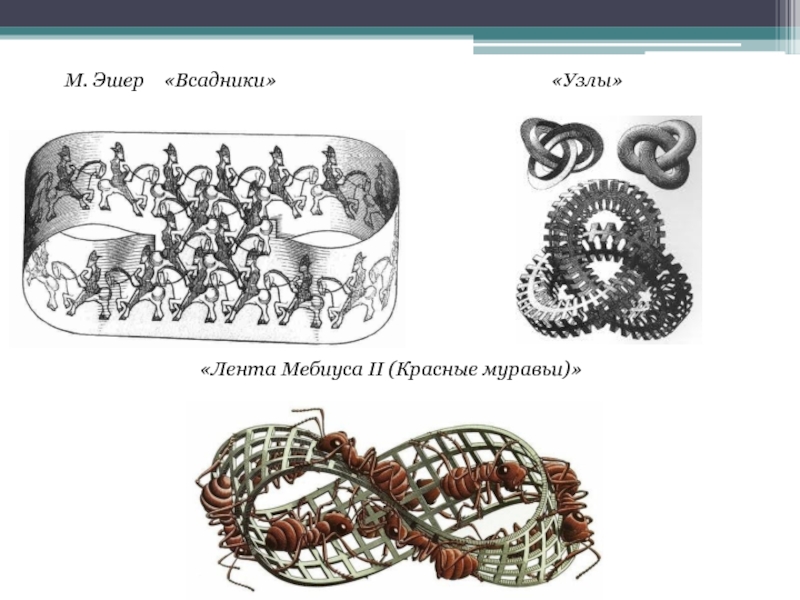
- 11. Лента Мебиуса - это трехмерный объект,
- 12. М. Эшер «Всадники»
- 13. Искаженные и необычные перспективы
- 14. М.Эшер «Наверху и внизу» «Дом лестниц» «Картинная галерея»
- 15. Невозможные фигуры - эти фигура, изображенная
- 16. Одним из примеров невозможной фигуры
- 17. Фрактал - это объект, повторяющий
- 18. Роберт Фатауэр "Композиция кругов" (2001) -
- 19. Математические изобразительное искусство процветает сегодня,
- 20. Нет ни одной области математики,
- 21. Источники: http://im-possible.info/russian/articles/vis_math_art/ http://mcesher.ru/
Слайд 1Октябрьский Нефтяной Колледж
Выполнил
студент группы 1Б3-16
Валиахметов Р.И.
Проверил..
Октябрьский 2016
Математика и искусство
Слайд 2 Математика - царица всех наук, символ мудрости. Красота математики
Слайд 3 Искусство - творческое отражение, воспроизведение действительности в художественных образах.
Слайд 4 Математика владеет не только истиной, но и высшей красотой
Бертран Рассел
Слайд 5 К фундаментальным понятиям симметрии относятся плоскость симметрии, ось симметрии,
Принцип "симметрии" широко используется в искусстве. Бордюры в архитектурных и скульптурных произведениях, орнаменты в прикладном искусстве, - все это примеры использования симметрии.
Принцип симметрии очень часто используется совместно с принципом "золотого сечения".
Слайд 6 Общие темы в математическом искусстве
Слайд 7 Многогранник - это трехмерное тело, гранями которого являются многоугольники.
Слайд 9 Тесселляции, известные также как покрытие плоскости плитками, являются коллекциями
Слайд 10 Роберт Фатауэр "Фрактальные рыбы - сгруппированные группы". Это компьютерная
Слайд 11 Лента Мебиуса - это трехмерный объект, имеющий только одну сторону.
Позднее, поверхности минимальной энергии стали вдохновением для многих математических художников. Брент Коллинз (Brent Collins), использует ленты Мебиуса и поверхности минимальной энергии, а также другие виды абстракций в скульптуре.
Слайд 13 Искаженные и необычные перспективы
Необычные системы перспективы,
Дик Термес "Клетка для человека" (1978). Это разукрашенная сфера, в процессе создания которой использовалась шеститочечная перспектива. На ней изображения геометрическая структура в виде сетки, сквозь которую виден ландшафт. Три ветки проникают внутрь клетки, а также по ней ползают рептилии. В то время как одни изучают мир, другие обнаруживают себя, находящимися в клетке.
Слайд 15 Невозможные фигуры - эти фигура, изображенная в перспективе таким способом,
Слайд 16 Одним из примеров невозможной фигуры служит картина современного венгерского
На картине изображены мосты, которые не могут существовать в трехмерном пространстве. Например, есть отражения в воде, которые не могут быть исходными мостами.
Слайд 17 Фрактал - это объект, повторяющий сам себя в различных
Слайд 18 Роберт Фатауэр "Композиция кругов" (2001) - не является вычисляемым фракталом,
Кэри Митчелл "Будда" - компьютерная картина основанная на множестве Мандельброта, исследованного Бенуа Мандельбротом
Слайд 19 Математические изобразительное искусство процветает сегодня, и многие художники создают
Слайд 20 Нет ни одной области математики, как бы абстрактна она
Н.И. Лобачевский