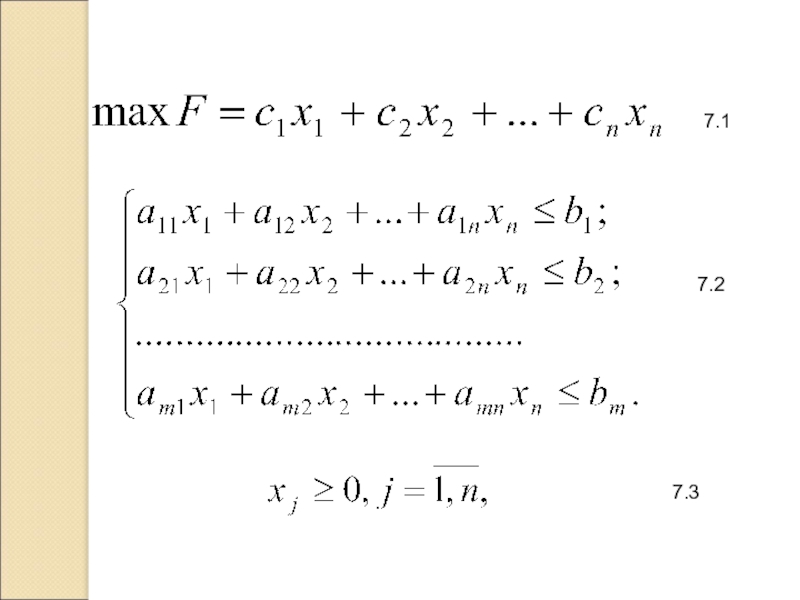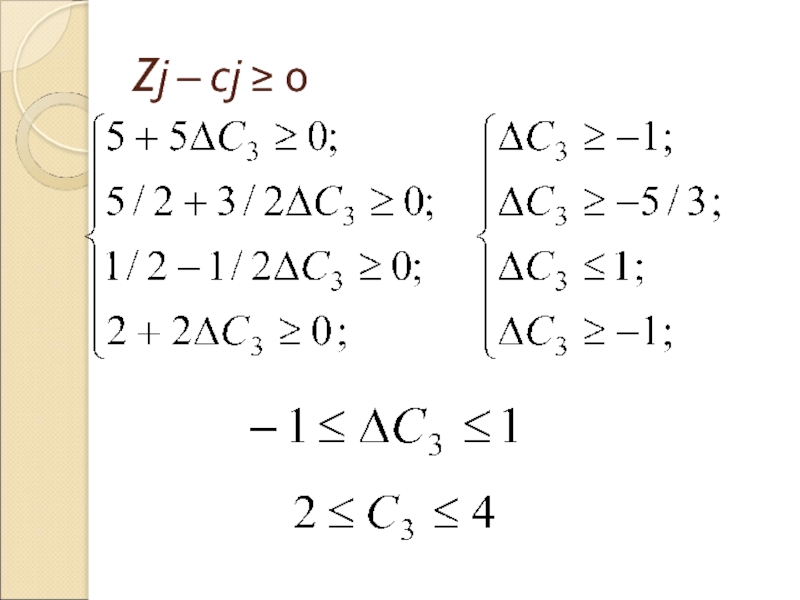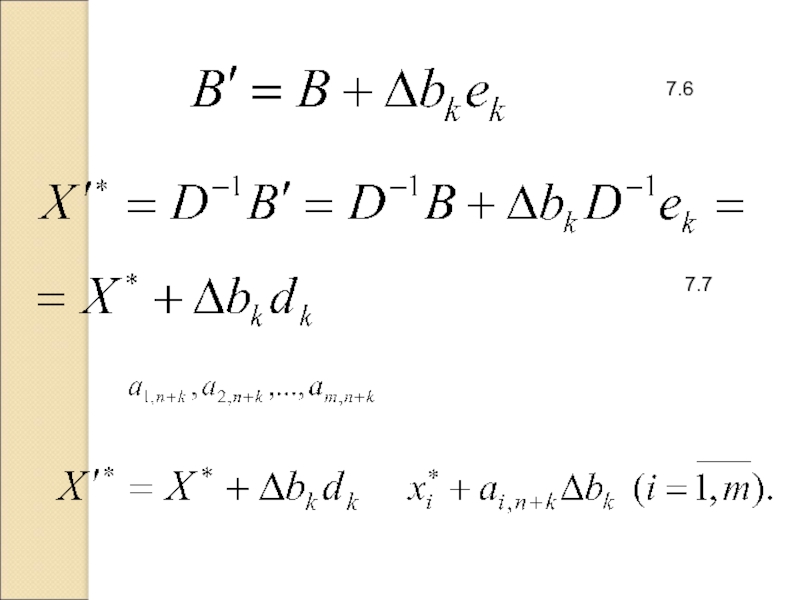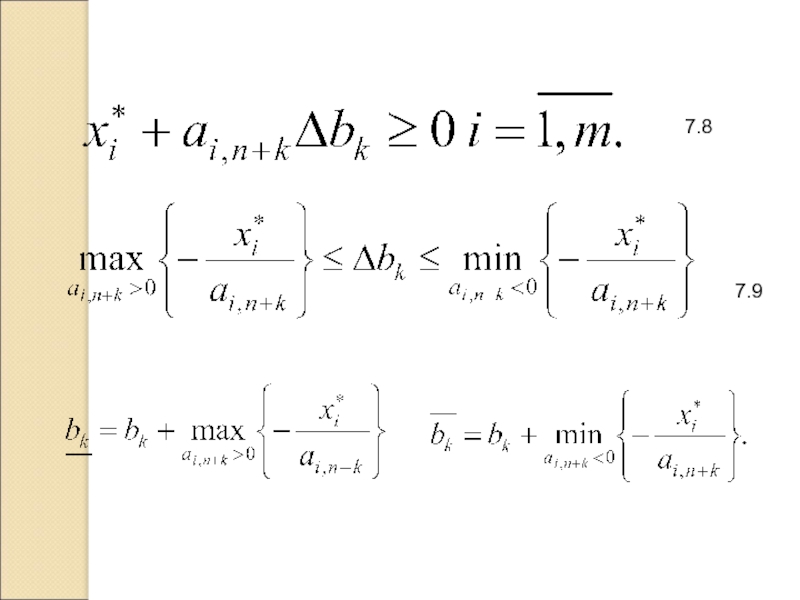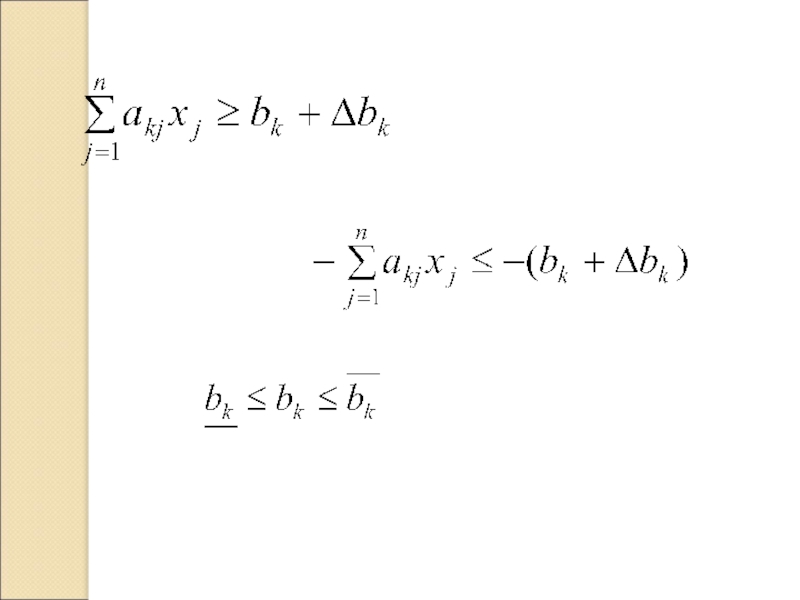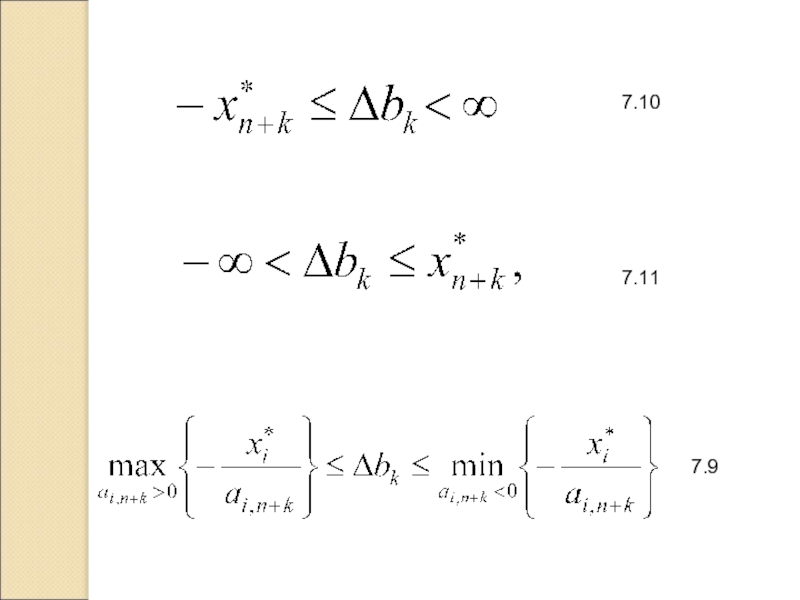- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Післяоптимізаційний аналіз задач лінійного програмування презентация
Содержание
- 1. Післяоптимізаційний аналіз задач лінійного програмування
- 2. План 7.1 Аналіз коефіцієнтів лінійних моделей: аналіз
- 3. 7.1 7.2 7.3
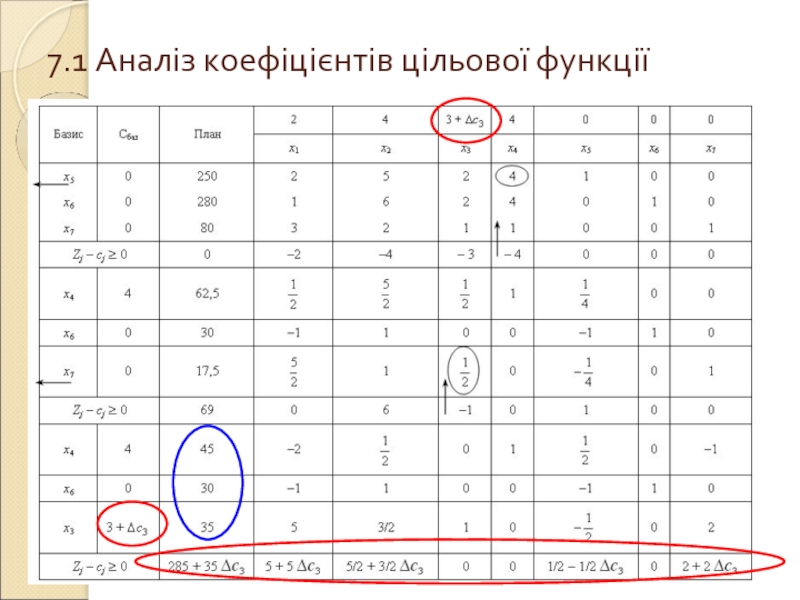
- 5. 7.1 Аналіз коефіцієнтів цільової функції
- 6. Для базисних змінних (F1–c1) = 4 ⋅
- 7. Zj – cj ≥ 0
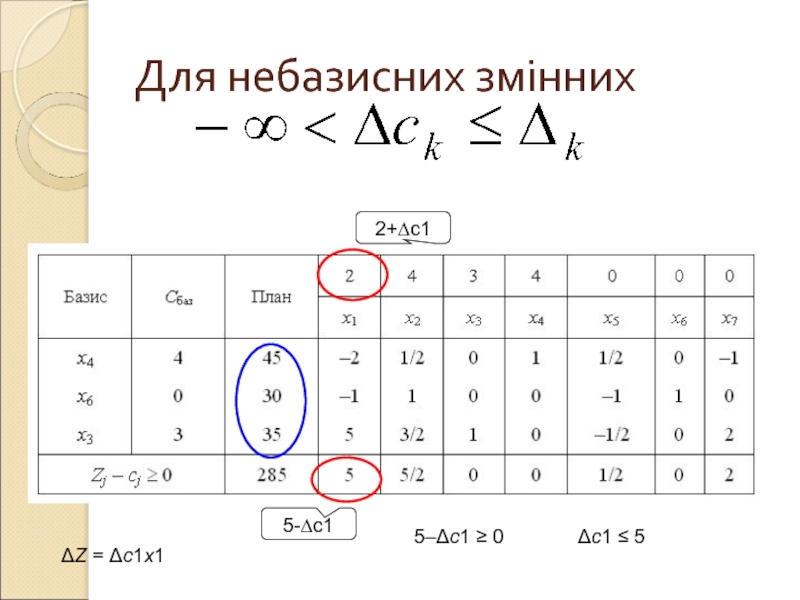
- 8. Для небазисних змінних 2+∆с1
- 9. 7.2 Аналіз діапазону зміни компонент вектора обмежень
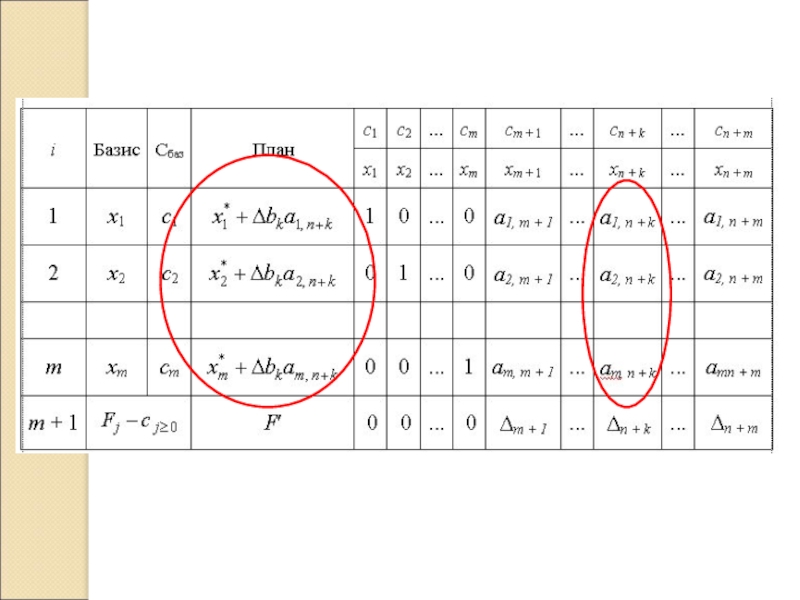
- 10. 7.6 7.7
- 12. 7.8 7.9
- 14. Додаткова змінна — базисна 7.7 7.8
- 15. 7.10 7.11 7.9
- 16. 7.3 Приклад практичного використання двоїстих оцінок у
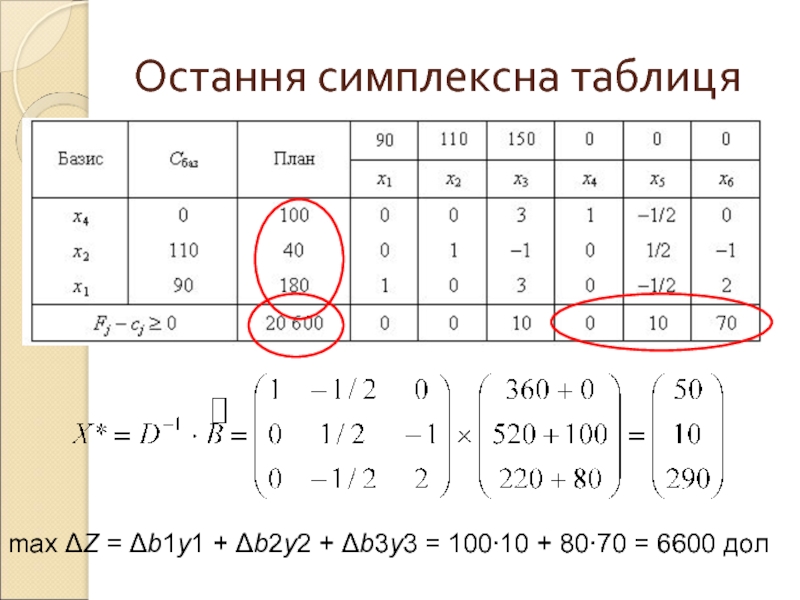
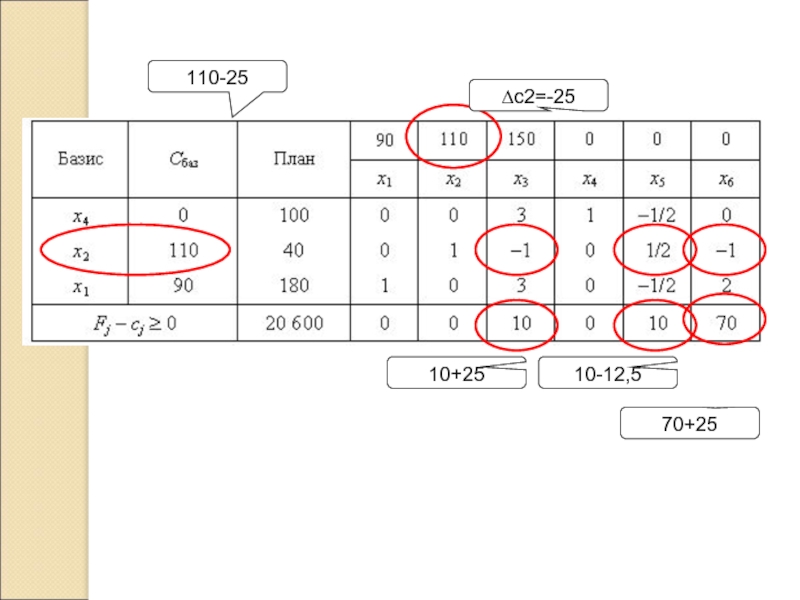
- 17. Остання симплексна таблиця
- 18. 110-25 10+25 ∆с2=-25 10-12,5 70+25
Слайд 2План
7.1 Аналіз коефіцієнтів лінійних моделей: аналіз коефіцієнтів цільової функції.
7.2 Аналіз діапазону
зміни компонент вектора обмежень.
7.3 Практичне використання двоїстих оцінок у аналізі економічної задачі (самостійна робота).
7.3 Практичне використання двоїстих оцінок у аналізі економічної задачі (самостійна робота).
Слайд 6Для базисних змінних
(F1–c1) = 4 ⋅ (–2) + 0 ⋅ (–1)
+(3 + Δc3)⋅ 5 – 2 = 5 + 5Δc3;
(F2–c2) = 4 ⋅ 1/2 + 0 ⋅ 1 + (3 + Δc3)⋅ 3/2 – 4 = 5/2 + 3/2Δc3;
(F5–c5) = 4 ⋅ 1/2 + 0 ⋅ (–1)+ (3 + Δc3) · (– 1/2 )– 0 = 1/2 – 1/2Δc3;
(F7–c7) = 4 ⋅ (–1) + 0 ⋅ 0 + (3 + Δc3) · 2 – 0 = 2 + 2Δc3
(F2–c2) = 4 ⋅ 1/2 + 0 ⋅ 1 + (3 + Δc3)⋅ 3/2 – 4 = 5/2 + 3/2Δc3;
(F5–c5) = 4 ⋅ 1/2 + 0 ⋅ (–1)+ (3 + Δc3) · (– 1/2 )– 0 = 1/2 – 1/2Δc3;
(F7–c7) = 4 ⋅ (–1) + 0 ⋅ 0 + (3 + Δc3) · 2 – 0 = 2 + 2Δc3
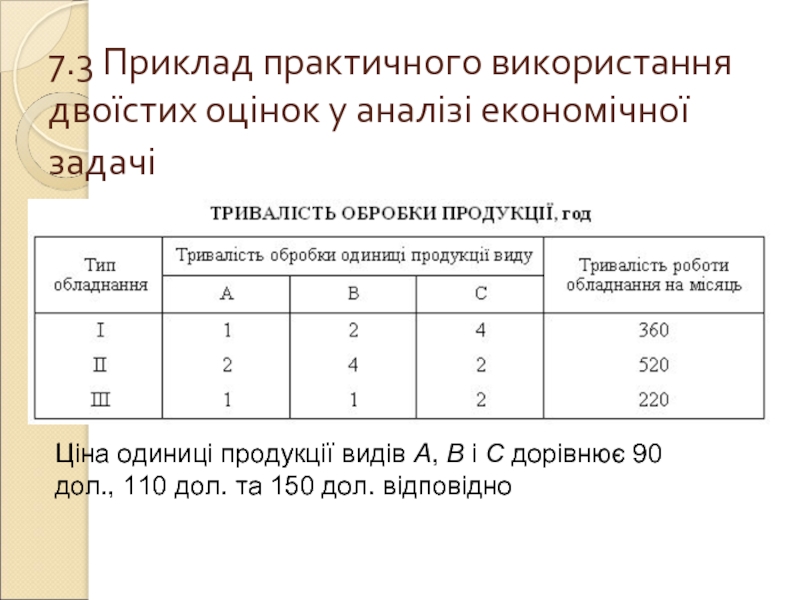
Слайд 167.3 Приклад практичного використання двоїстих оцінок у аналізі економічної задачі
Ціна
одиниці продукції видів А, В і С дорівнює 90 дол., 110 дол. та 150 дол. відповідно