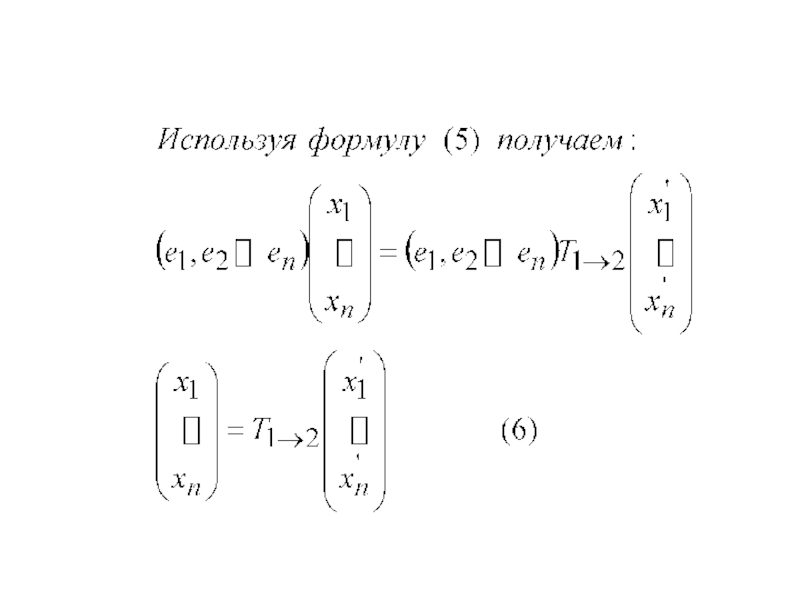- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Поля и линейные пространства презентация
Содержание
- 1. Поля и линейные пространства
- 2. Обозначения Заглавные латинские буквы (A, …)- множества Прописные латинские буквы (a,b…) – элементы множества
- 3. Поле Определение. Множество К называется полем, если
- 6. Простейшие свойства поля Нулевой элемент единственный Противоположный
- 7. Определение вычитания и деления в поле Определение.
- 8. Примеры полей Множество R – вещественных чисел
- 9. Линейное пространство. Определение. Множество V называется линейным
- 12. Простейшие следствия из аксиом ЛП Нулевой элемент единственный. Противоположный вектор единственный. Определение:
- 13. Линейная комбинация векторов V- ЛП Определение.
- 14. Линейная оболочка векторов Определение. Пусть
- 15. Выражение вектора через линейную комбинацию Определение. Если
- 16. Линейная зависимость Определение. Система векторов называется
- 17. Линейная независимость Определение. Система векторов
- 18. Алгебраические свойства систем линейных векторов. Если система
- 19. Геометрические свойства систем векторов. Система состоящая из
- 20. Базис линейного пространства V – ЛП Определение.
- 21. Размерность линейного пространства Определение. Количество векторов в базисе называется размерностью линейного пространства V. Обозначение. dimV=n.
- 22. Координаты вектора в базисе Из определения базиса
- 23. Координаты вектора в базисе Замечание. Координаты вектора
- 24. Подпространства линейного пространства
- 25. Подпространства и подмножества Определение. Подмножество W линейного
- 26. Примеры подпространств.
- 27. Равносильное определение. Утверждение. Множество W является линейным
- 40. Изменение координат вектора при замене базиса
- 41. Матрица перехода V – линейное пространство e1,
- 50. Свойства изоморфизма Рефлективность Симметричность Транзитивность
Слайд 2Обозначения
Заглавные латинские буквы (A, …)- множества
Прописные латинские буквы (a,b…) – элементы
множества
Слайд 3Поле
Определение. Множество К называется полем, если в нем введены две бинарные
операции: сложение и умножение
удовлетворяющие аксиомам:
удовлетворяющие аксиомам:
Слайд 6Простейшие свойства поля
Нулевой элемент единственный
Противоположный элемент единственный.
Единичный элемент единственный.
Обратный элемент единственный.
Слайд 7Определение вычитания и деления в поле
Определение.
Замечание. Такое определение корректно, благодаря единственности
противоположного и обратного элемента.
Слайд 8Примеры полей
Множество R – вещественных чисел является полем
Множество Q - рациональных
чисел является полем.
Множество F2 ={0,1} – из двух элементов является полем
Множество F2 ={0,1} – из двух элементов является полем
Слайд 9Линейное пространство.
Определение. Множество V называется линейным пространством над полем K, если
в нем введены две бинарные операции: сложение и умножение на число из поля
удовлетворяющие аксиомам:
удовлетворяющие аксиомам:
Слайд 12Простейшие следствия из аксиом ЛП
Нулевой элемент единственный.
Противоположный вектор единственный.
Определение:
Слайд 13Линейная комбинация векторов
V- ЛП
Определение. Выражение вида
называется линейной комбинацией векторов
Слайд 14Линейная оболочка векторов
Определение. Пусть
- система векторов. Множество всех линейных комбинаций данной системы векторов называют линейной оболочкой системы векторов:
Слайд 15Выражение вектора через линейную комбинацию
Определение. Если некоторый вектор
представлен в виде
то говорят, что вектор линейно выражается через вектора
Слайд 16Линейная зависимость
Определение. Система векторов называется
линейно зависимой, если существует ненулевой набор чисел
таких, что
таких, что
Слайд 17Линейная независимость
Определение. Система векторов
называется линейно независимой, если
тогда и
только тогда, когда все числа
равны нулю.
равны нулю.
Слайд 18Алгебраические свойства систем линейных векторов.
Если система векторов содержит нулевой вектор, то
она линейно зависима.
Если часть системы векторов (подсистема) линейно зависима, то и вся система векторов тоже линейно зависима.
Система векторов линейно зависима тогда и только тогда, когда существует вектор, линейно выражающийся через остальные вектора
Если часть системы векторов (подсистема) линейно зависима, то и вся система векторов тоже линейно зависима.
Система векторов линейно зависима тогда и только тогда, когда существует вектор, линейно выражающийся через остальные вектора
Слайд 19Геометрические свойства систем векторов.
Система состоящая из одного вектора линейно зависима тогда
и только тогда, когда этот вектор нулевой.
Система состоящая из двух векторов линейно зависима тогда и только тогда, когда вектора коллинеарны.
Система состоящая из трех векторов линейно зависима тогда и только тогда, когда три вектора компланарны.
Система состоящая из двух векторов линейно зависима тогда и только тогда, когда вектора коллинеарны.
Система состоящая из трех векторов линейно зависима тогда и только тогда, когда три вектора компланарны.
Слайд 20Базис линейного пространства
V – ЛП
Определение. Система векторов
называется базисом ЛП V,
если эта система ЛНЗ и любой вектор из V линейно выражается через
Замечание. В ЛП V базис определяется не единственным образом (можно выбрать несколько базисов), но количество базисных векторов n остается неизменной величиной.
если эта система ЛНЗ и любой вектор из V линейно выражается через
Замечание. В ЛП V базис определяется не единственным образом (можно выбрать несколько базисов), но количество базисных векторов n остается неизменной величиной.
Слайд 21Размерность линейного пространства
Определение. Количество векторов в базисе называется размерностью линейного пространства
V.
Обозначение. dimV=n.
Обозначение. dimV=n.
Слайд 22Координаты вектора в базисе
Из определения базиса ЛП V следует, что любой
вектор в этом ЛП линейно выражается через базисные векторы :
Определение. Координатами вектора x называются коэффициенты в разложении по базисным векторам:
Определение. Координатами вектора x называются коэффициенты в разложении по базисным векторам:
Слайд 23Координаты вектора в базисе
Замечание. Координаты вектора x зависят от выбора базиса.
В разных базисах у одного и того же вектора x разные координаты.
Слайд 25Подпространства и подмножества
Определение. Подмножество W линейного пространства V называется линейным подпространством,
если оно является линейным пространством относительно операций из V.
Обозначение.
Утверждение. (ноль принадлежит любому подпространству)
Утверждение. Для любого линейного пространства V подмножества {0} и V являются подпространствами.
Обозначение.
Утверждение. (ноль принадлежит любому подпространству)
Утверждение. Для любого линейного пространства V подмножества {0} и V являются подпространствами.
Слайд 27Равносильное определение.
Утверждение. Множество W является линейным подпространством V тогда и только
тогда, когда оно замкнуто относительно операций сложения и умножения на число:
Слайд 41Матрица перехода
V – линейное пространство
e1, e2,e3…..en – первый базис (1)
e’1, e’2,e’3,…e’n
– второй базис (2)
(количество векторов n=dimV, но сами вектора разные)
Выразим вектора второго базиса через вектора первого базиса:
(количество векторов n=dimV, но сами вектора разные)
Выразим вектора второго базиса через вектора первого базиса: