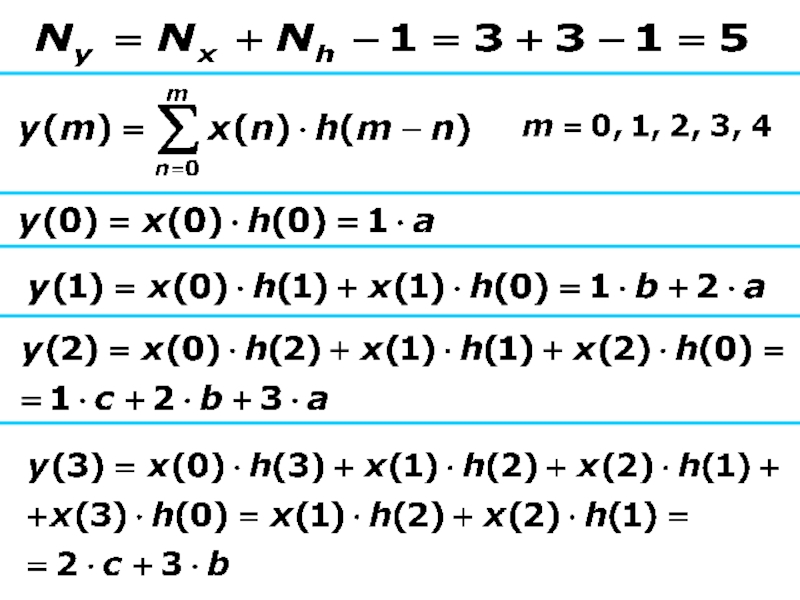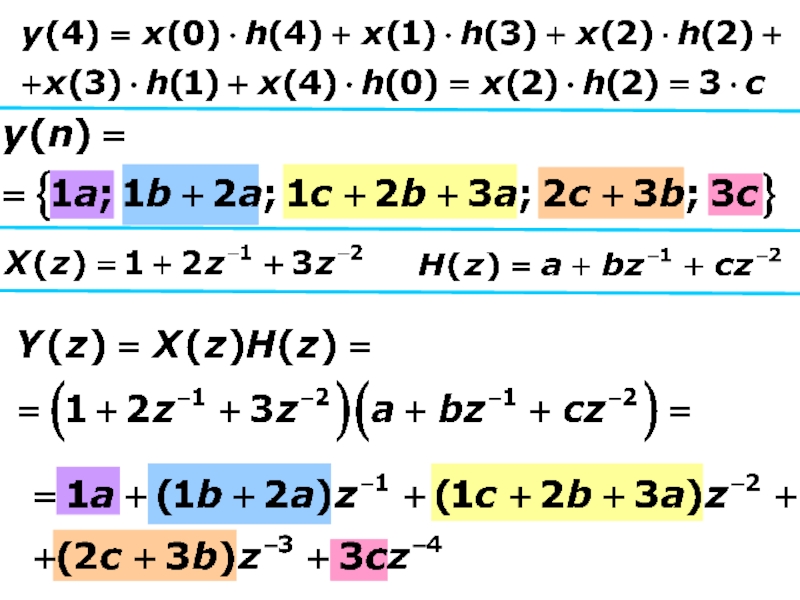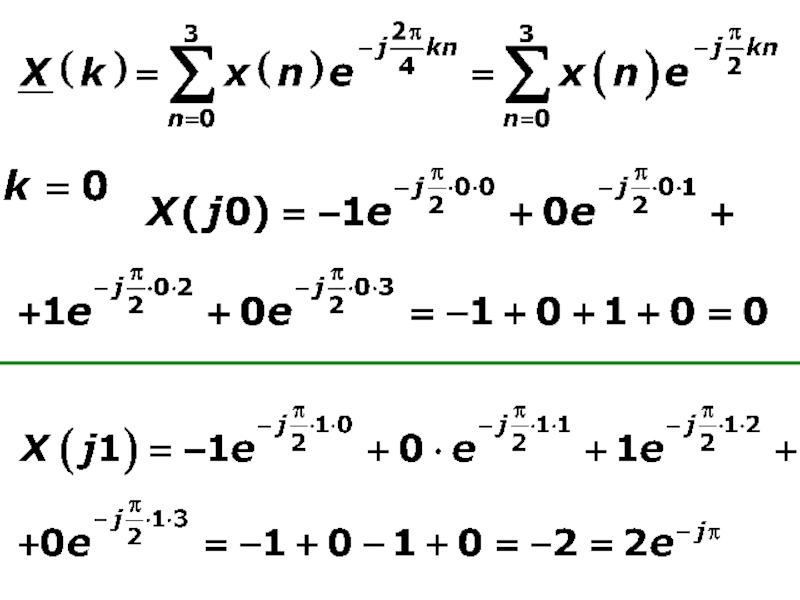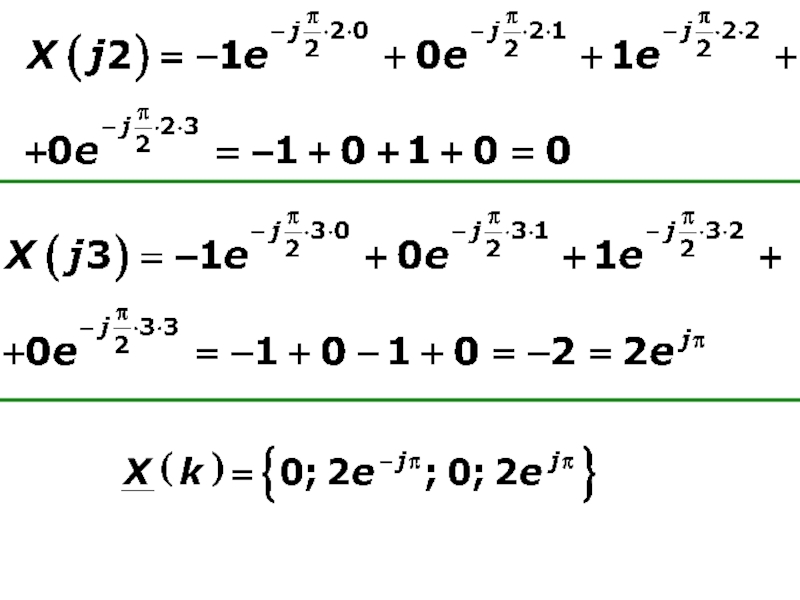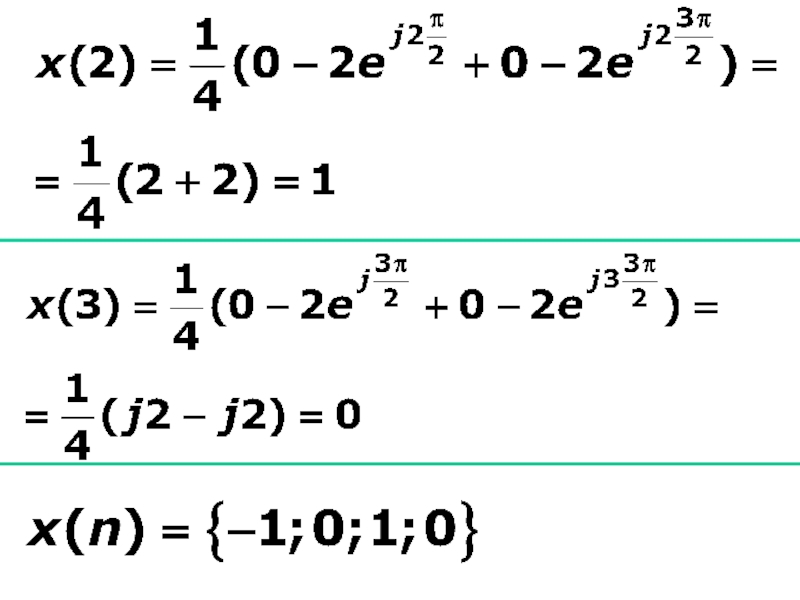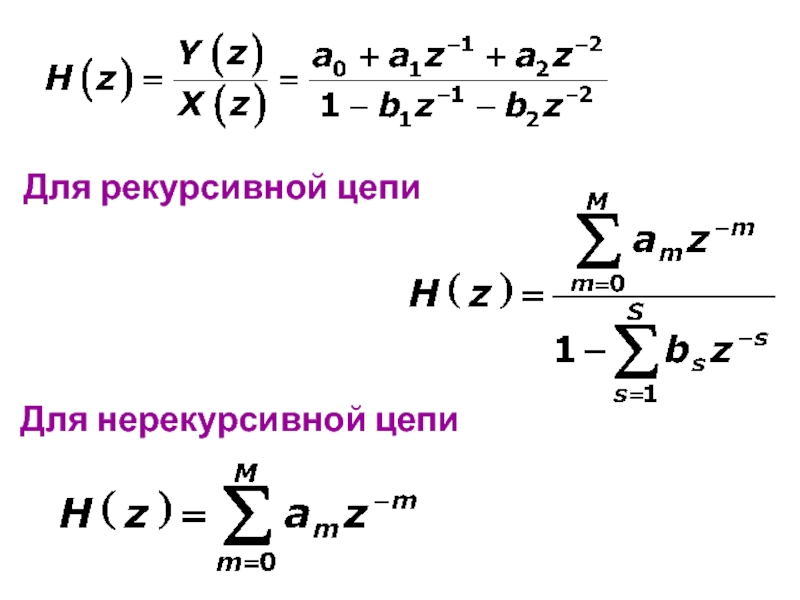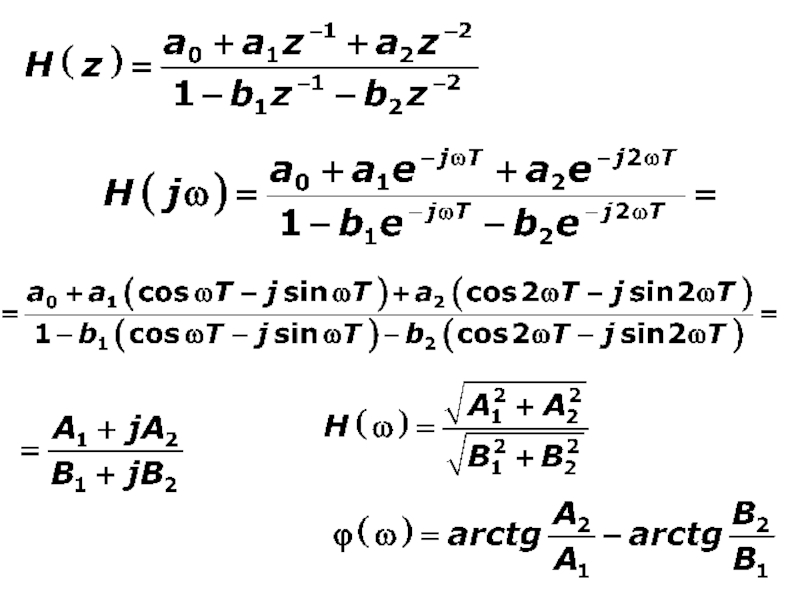- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
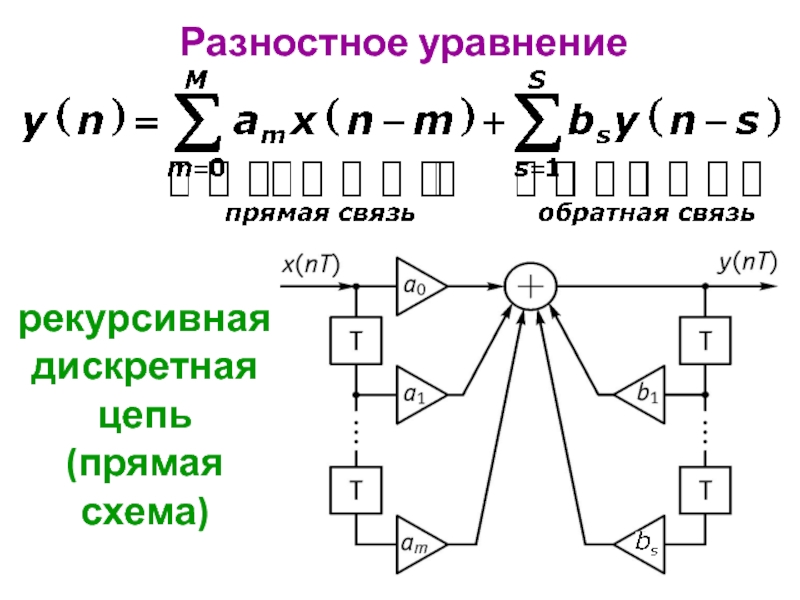
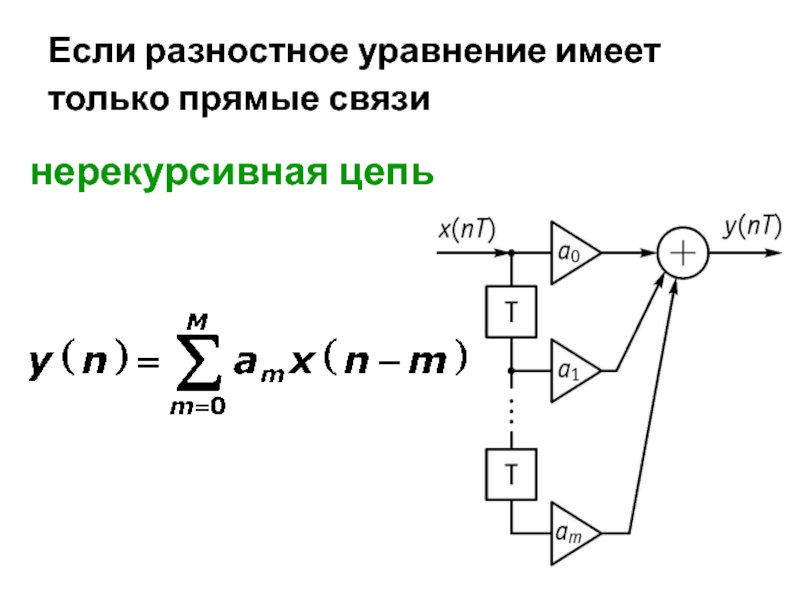
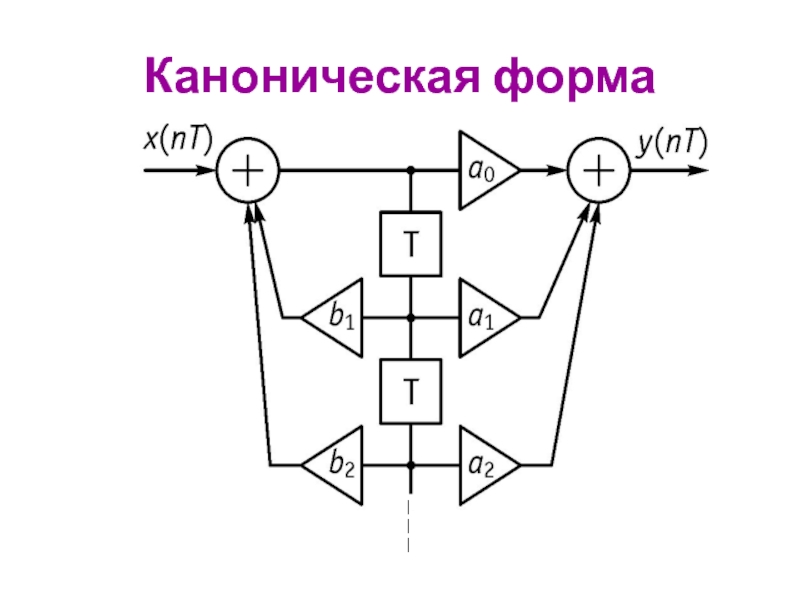
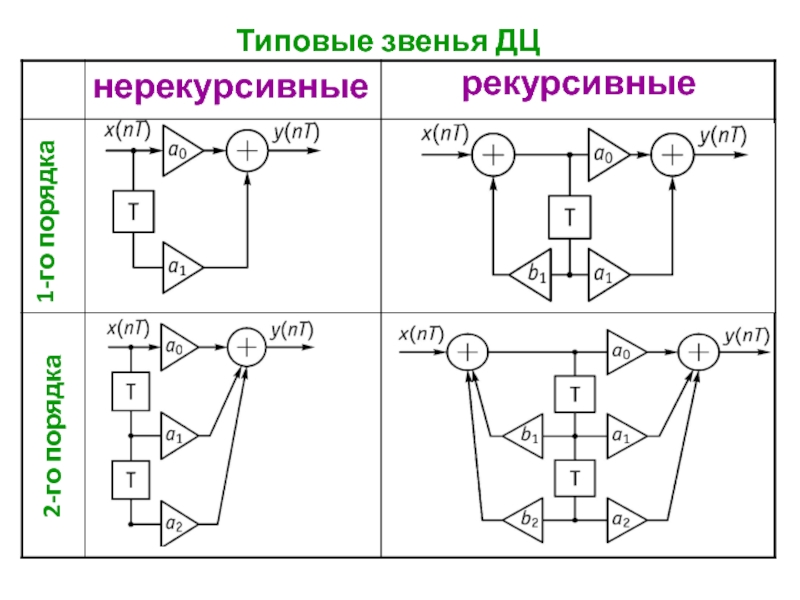
Математические основы цифровой обработки сигнала презентация
Содержание
- 1. Математические основы цифровой обработки сигнала
- 2. Литература Гоноровский И.С. Радиотехнические цепи и сигналы:
- 3. Карташев В.Г. Основы теории дискретных сигналов и
- 4. Дискретные сигналы
- 5. Аналоговый сигнал – непрерывная или кусочно-непрерывная функция
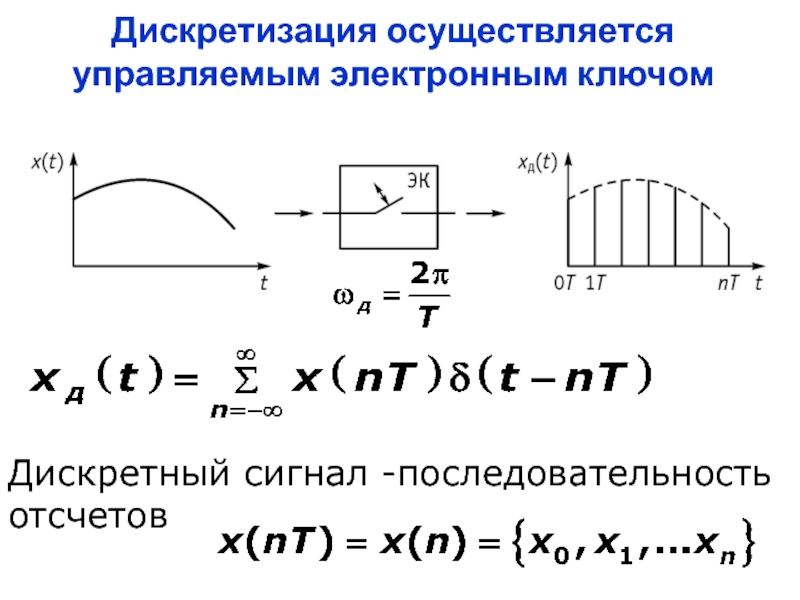
- 6. Дискретизация осуществляется управляемым электронным ключом Дискретный сигнал -последовательность отсчетов
- 7. Теорема Котельникова Если функция x(t) имеет
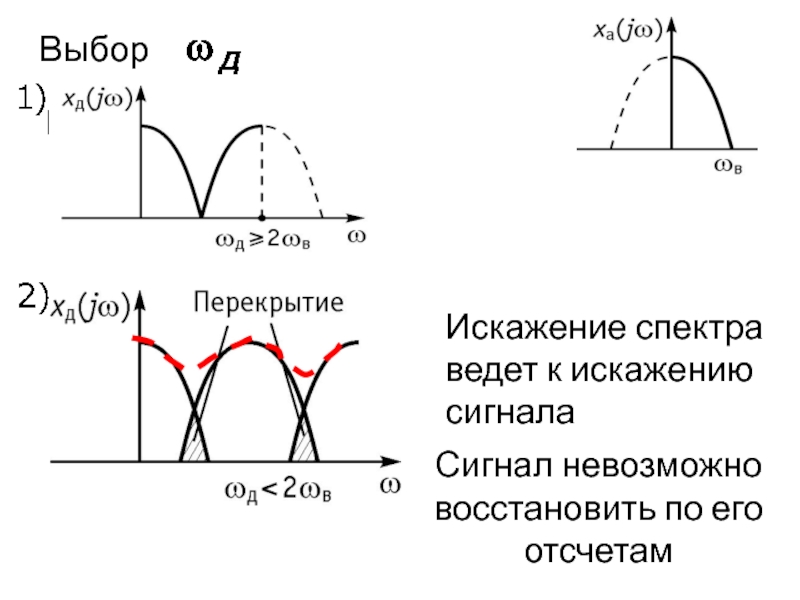
- 8. Выбор Искажение спектра ведет к искажению сигнала Сигнал невозможно восстановить по его отсчетам
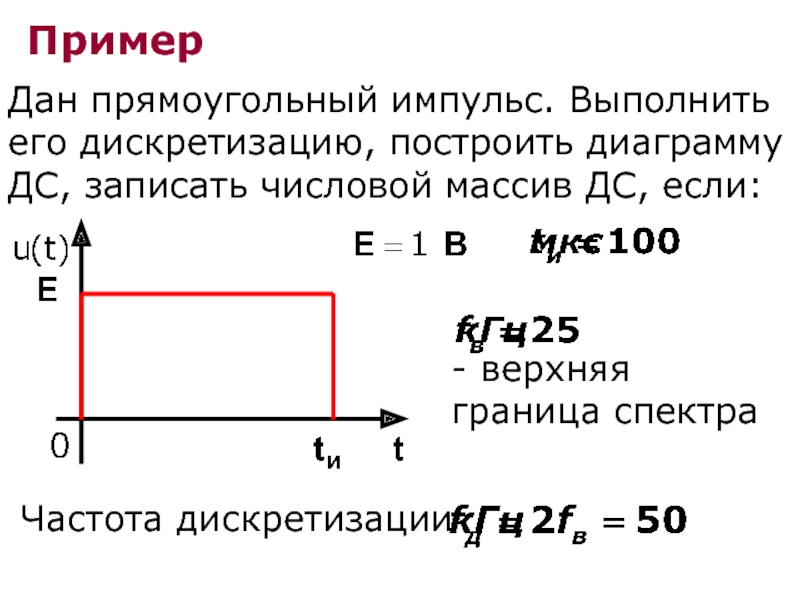
- 9. Пример Дан прямоугольный импульс. Выполнить его дискретизацию,
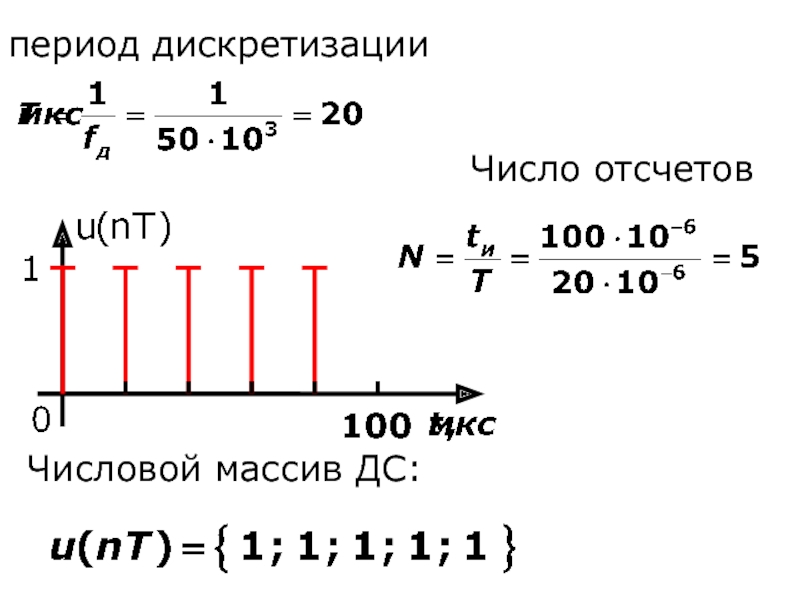
- 10. Числовой массив ДС: период дискретизации Число отсчетов
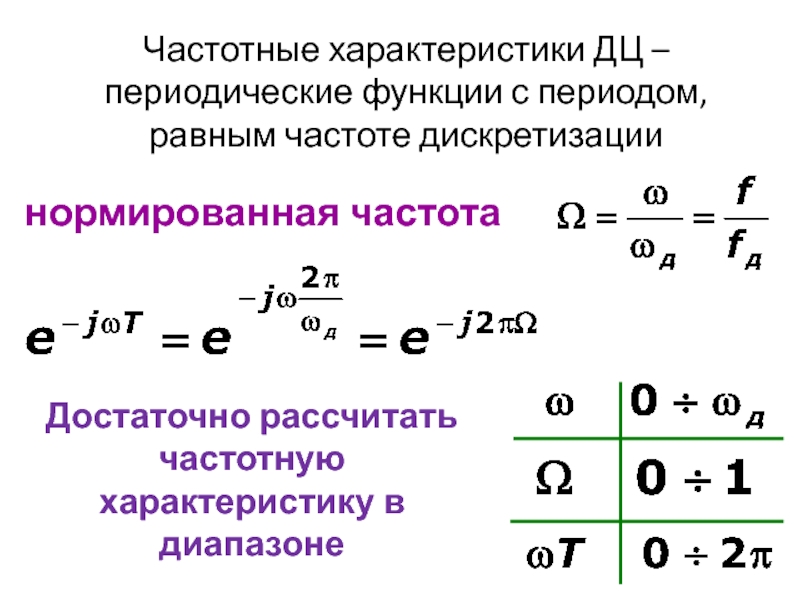
- 11. позволяет определить спектр дискретного сигнала
- 12. Спектр дискретного сигнала представляет собой периодическое повторение
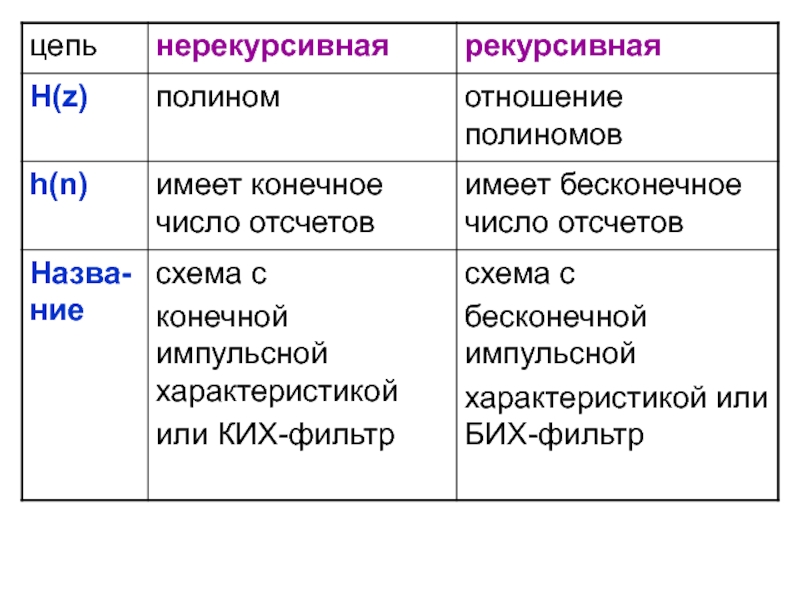
- 13. дискретный сигнал его Z-изображение Z-преобразование
- 14. Свойства Z-преобразования Свойство однозначности: каждой последовательности
- 15. 3. Теорема запаздывания: если
- 16. Выполнить линейную свертку входного сигнала
- 19. Z-изображения некоторых функций
- 20. Методы определения сигналов по его z-изображению 1. С
- 21. использование теоремы о вычетах Пример
- 22. Решение: приведем X(z) к виду полюсы X(z): тогда:
- 23. коэффициенты :
- 24. дискретный сигнал
- 25. отчеты ДС:
- 26. Пример Приведение функции к табличной
- 27. Пример
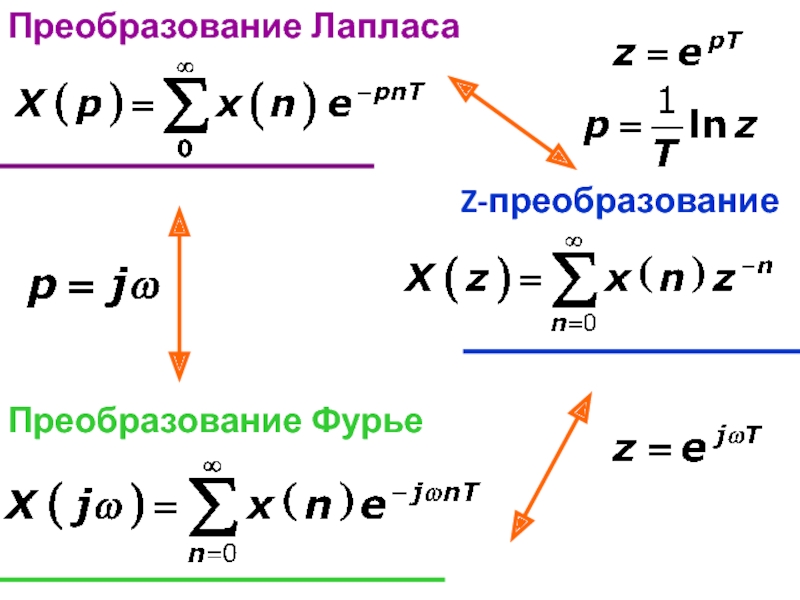
- 28. Преобразование Лапласа Z-преобразование Преобразование Фурье
- 29. Преобразование точек р плоскости в точки Z-плоскости
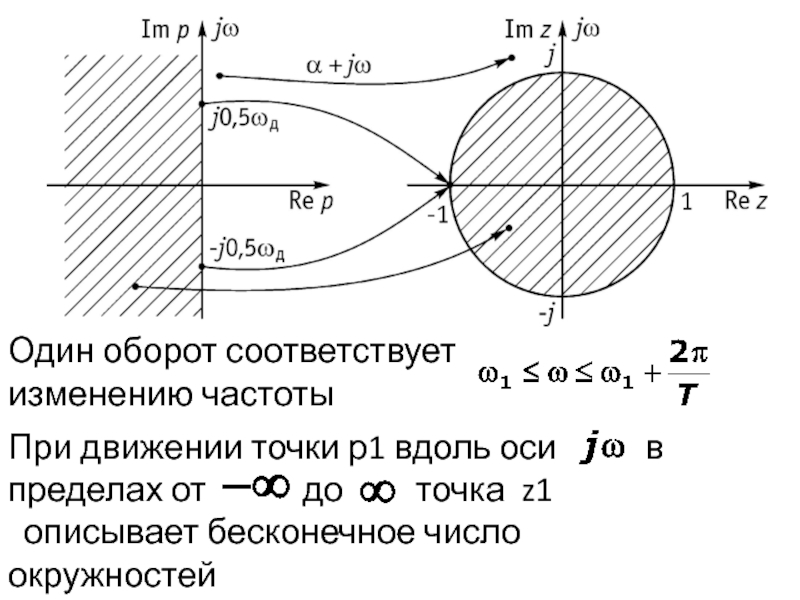
- 30. Один оборот соответствует изменению частоты При движении
- 31. Взаимно-однозначное отображение p на z существует
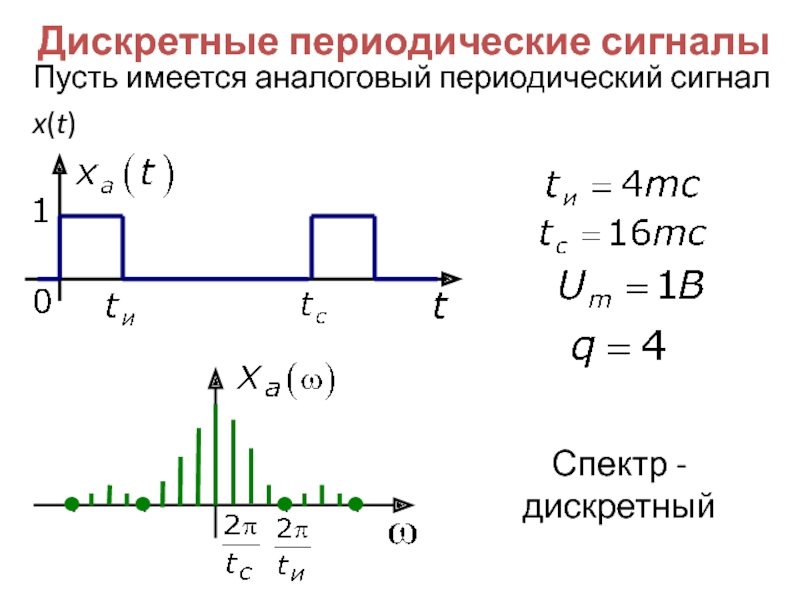
- 32. Пусть имеется аналоговый периодический сигнал x(t) Спектр -дискретный Дискретные периодические сигналы
- 33. Произведем дискретизацию аналогового сигнала с периодом T
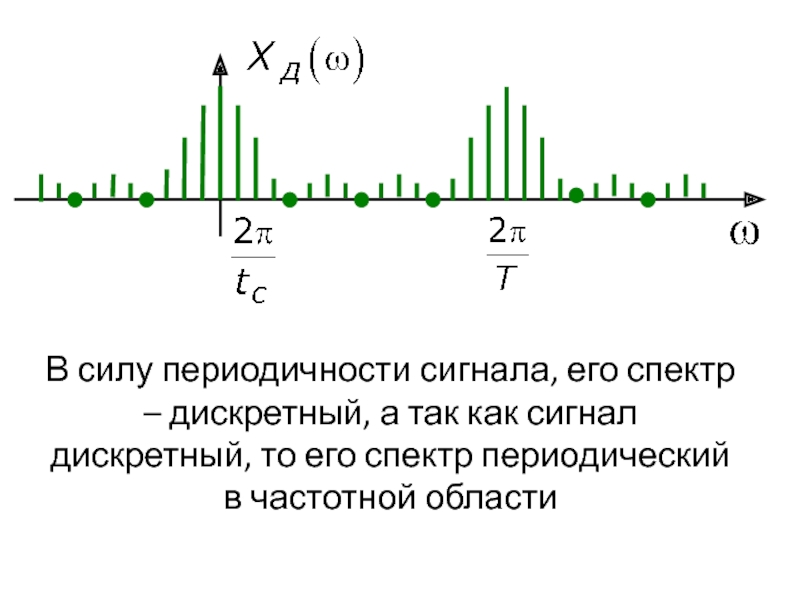
- 34. В силу периодичности сигнала, его спектр –
- 35. Дискретное преобразование Фурье (ДПФ) для
- 36. Огибающая спектра периодического дискретного сигнала совпадает со
- 37. Комплексные числа
- 38. Действия над комплексными числами Сложение и вычитание
- 39. Комплексно-сопряженные числа 4. Извлечение корня
- 40. Пример Применить прямое ДПФ к сигналу Делаем сигнал периодическим и ОДПФ к полученным коэффициентам ДПФ
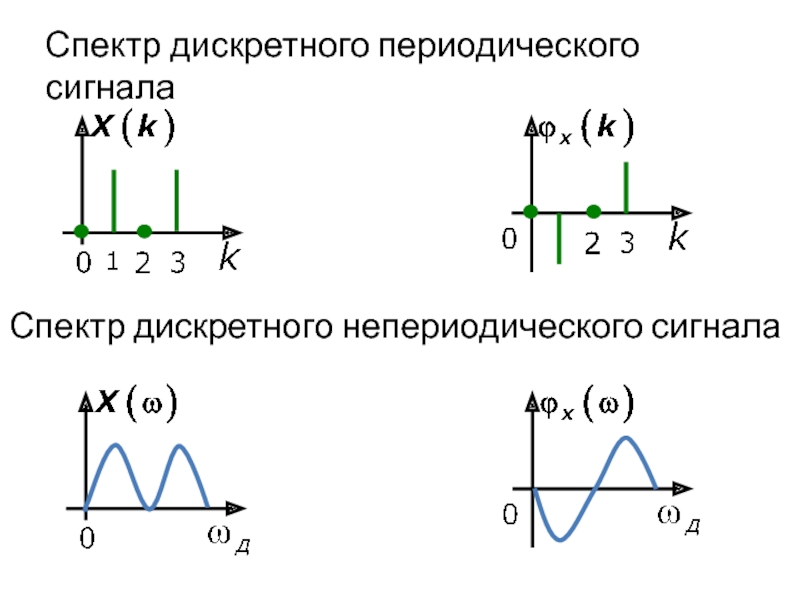
- 43. Спектр дискретного периодического сигнала Спектр дискретного непериодического сигнала
- 44. Рассчитаем отсчеты
Литература Гоноровский И.С. Радиотехнические цепи и сигналы: Учеб для вузов. – М.: Радио и связь, 1994. Гольденберг Л.М. и др. Цифровая обработка сигналов: Справочник. – М.: Радио и связь, 1985.
Слайд 2Литература
Гоноровский И.С. Радиотехнические цепи и сигналы: Учеб для вузов. – М.:
Радио и связь, 1994.
Гольденберг Л.М. и др. Цифровая обработка сигналов: Справочник. – М.: Радио и связь, 1985.
Гольденберг Л.М. и др. Цифровая обработка сигналов: Справочник. – М.: Радио и связь, 1985.
Слайд 3Карташев В.Г. Основы теории дискретных сигналов и цифровых фильтров. – М.:
Высшая школа, 1982.
Солонина А.И., Улахович Д.А., Арбузов С.М., Соловьева Е.Б., Гук И.И.. Основы цифровой обработки сигналов: Курс лекций. – СПб.: БХВ-Петербург, 2003.
Солонина А.И., Улахович Д.А., Арбузов С.М., Соловьева Е.Б., Гук И.И.. Основы цифровой обработки сигналов: Курс лекций. – СПб.: БХВ-Петербург, 2003.
Слайд 5Аналоговый сигнал – непрерывная или кусочно-непрерывная функция x(t)
Дискретный сигнал (ДС)
– последовательность отсчетов функции x(t), взятой в определенные моменты времени: 0Т, 1Т, 2Т, …, nТ, где Т – интервал времени, через которые берутся отсчеты (период дискретизации)
Дискретизация аналогового сигнала – процесс преобразования аналогового сигнала в последовательность временных отсчетов
Дискретизация аналогового сигнала – процесс преобразования аналогового сигнала в последовательность временных отсчетов
Слайд 6Дискретизация осуществляется управляемым электронным ключом
Дискретный сигнал -последовательность отсчетов
Слайд 7
Теорема Котельникова
Если функция x(t) имеет спектр, ограниченный некоторой частотой
, то сигнал x(t) может быть полностью восстановлен по его отсчетам, взятым через время
Слайд 8Выбор
Искажение спектра ведет к искажению сигнала
Сигнал невозможно восстановить по его
отсчетам
Слайд 9Пример
Дан прямоугольный импульс. Выполнить его дискретизацию, построить диаграмму ДС, записать числовой
массив ДС, если:
- верхняя граница спектра
Частота дискретизации
Слайд 11
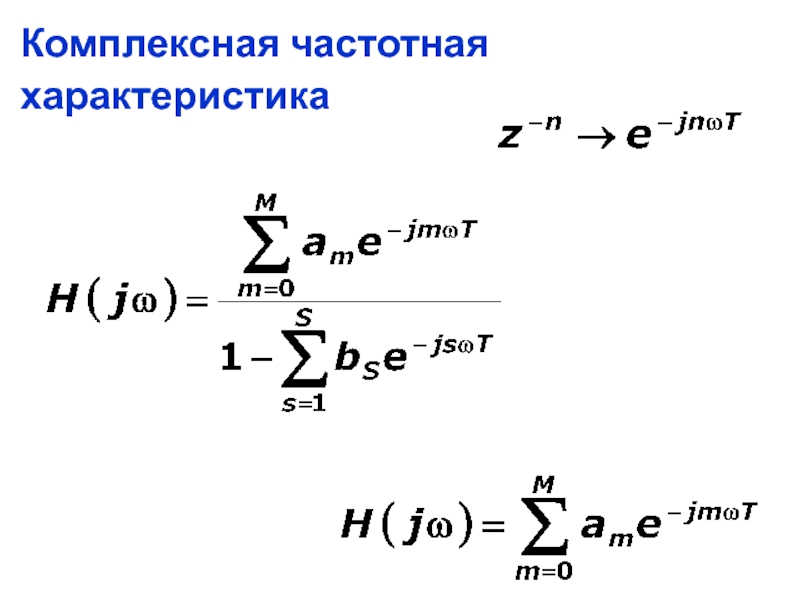
позволяет определить спектр дискретного сигнала по последовательности его отсчетов
Преобразование Фурье
Дискретные непериодические
сигналы
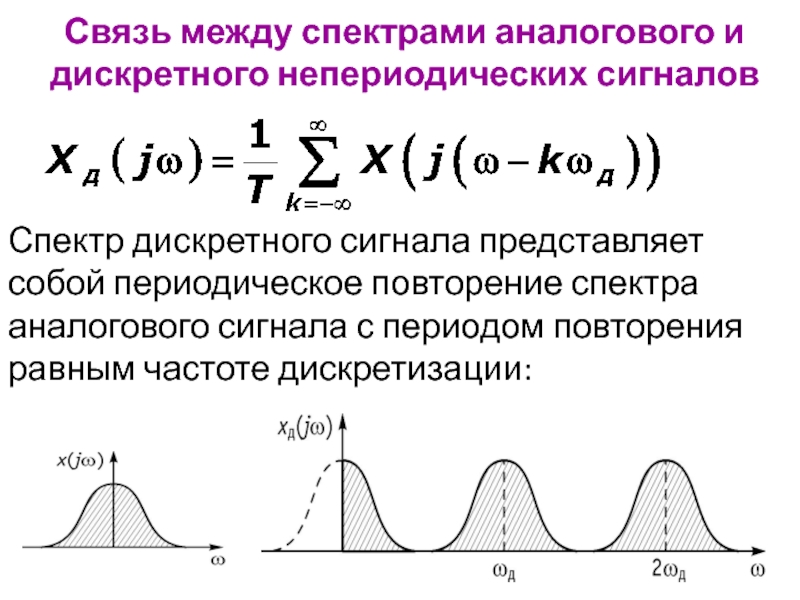
Слайд 12Спектр дискретного сигнала представляет собой периодическое повторение спектра аналогового сигнала с
периодом повторения равным частоте дискретизации:
Связь между спектрами аналогового и дискретного непериодических сигналов
Слайд 13
дискретный сигнал
его Z-изображение
Z-преобразование дискретного сигнала
получаются из формул преобразования Фурье для дискретного
сигнала путем замены:
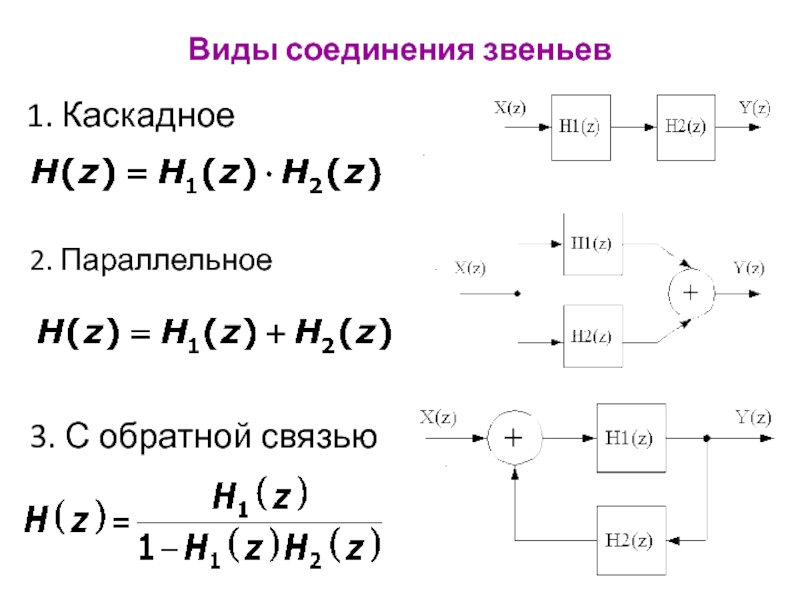
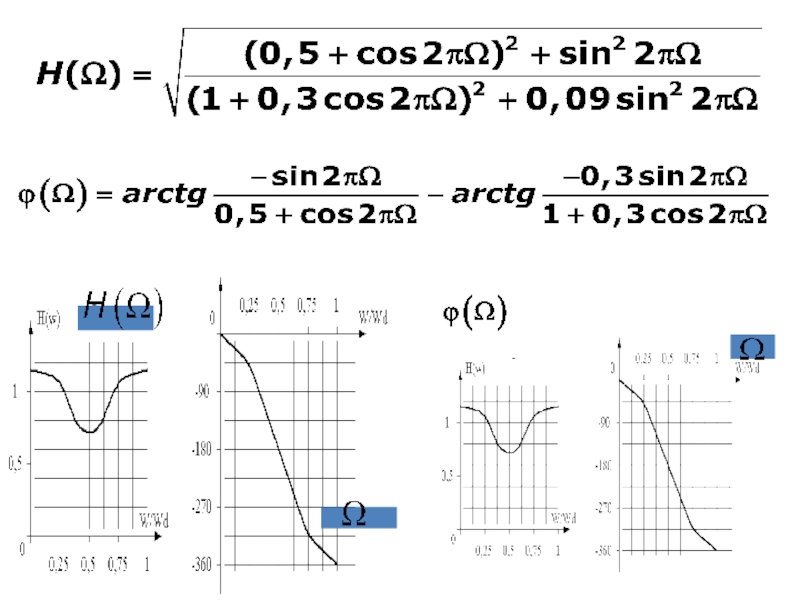
Слайд 14Свойства Z-преобразования
Свойство однозначности: каждой последовательности
соответствует одно и только одно z-преобразование.
Линейность:
Линейность:
Слайд 153. Теорема запаздывания:
если
, тогда
4. Теорема свертки: свертка сигналов соответствует умножению их z-преобразований
4. Теорема свертки: свертка сигналов соответствует умножению их z-преобразований
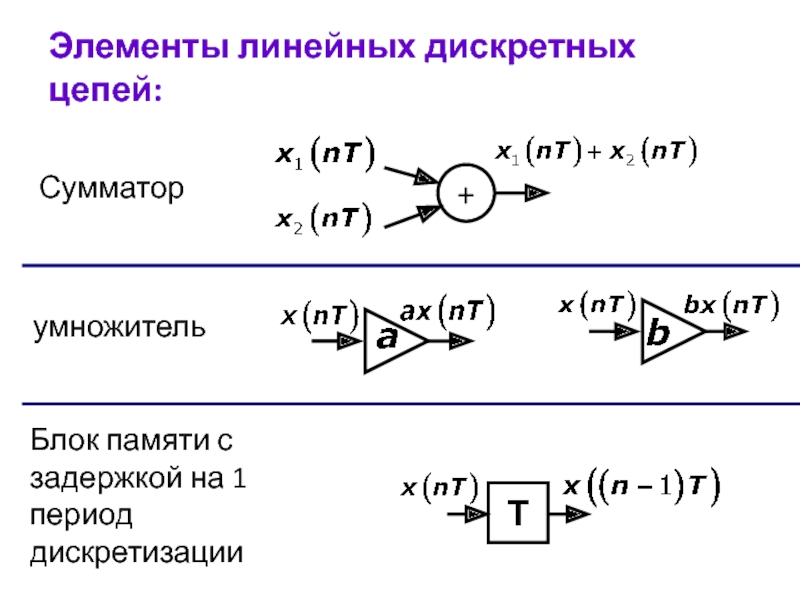
Слайд 16Выполнить линейную свертку
входного сигнала
и импульсной характеристики
Пример
Решение
длина выходной последовательности
- длина входной последовательности
- длина импульсной характеристики
Слайд 20Методы определения сигналов по его z-изображению
1. С помощью теоремы вычетов
3. Метод непрерывного деления
полинома числителя на полином знаменателя
2.Приведение функции к табличной
Если
то
Слайд 29Преобразование точек р плоскости в точки Z-плоскости
При движении точки на плоскости
Р вдоль оси , т.е. при , соответствующая ей точка плоскости Z описывает окружность единичного радиуса
- комплексное число
Слайд 30Один оборот соответствует изменению частоты
При движении точки р1 вдоль оси
в
пределах от до точка z1
описывает бесконечное число
окружностей
пределах от до точка z1
описывает бесконечное число
окружностей
Слайд 31
Взаимно-однозначное отображение p на z существует только для полосы р -
плоскости в пределах (левая полуплоскость - внутрь единичного круга, правая – во всю остальную z-плоскость)
Все параллельные полосы р-плоскости такой же ширины также отображаются на всю z-плоскость.
Все параллельные полосы р-плоскости такой же ширины также отображаются на всю z-плоскость.
С помощью ряда Тейлора
Билинейное Z-преобразование
Слайд 32Пусть имеется аналоговый периодический сигнал x(t)
Спектр -дискретный
Дискретные периодические сигналы
Слайд 33Произведем дискретизацию аналогового сигнала с периодом T = 1 мс
Дискретизация
периодического сигнала осуществляется на интервале, равном его периоду
- число отсчетов сигнала на периоде
Слайд 34В силу периодичности сигнала, его спектр – дискретный, а так как
сигнал дискретный, то его спектр периодический в частотной области
Слайд 35Дискретное преобразование Фурье (ДПФ)
для дискретного периодического сигнала,
имеющего периодический дискретный спектр
Число
отсчетов сигнала и число отсчетов его спектра одинаковы на периоде повторения
Слайд 36Огибающая спектра периодического дискретного сигнала совпадает со спектром дискретного непериодического сигнала.
Можно определить спектр непериодического сигнала, используя ДПФ, для этого необходимо сделать его периодическим
Слайд 37Комплексные числа
Алгебраическая форма записи
числа
Показательная форма записи
числа
Переход от одной формы
к другой
Слайд 38Действия над комплексными числами
Сложение и вычитание (в алгебраической форме)
Умножение (в показательной
форме)
Деление (в показательной форме)
Деление (в показательной форме)
Слайд 40Пример
Применить прямое ДПФ к сигналу
Делаем сигнал периодическим
и ОДПФ к полученным коэффициентам
ДПФ
