- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Параллельность прямых в пространстве презентация
Содержание
- 1. Параллельность прямых в пространстве
- 2. ЦЕЛИ УРОКА 1. Рассмотреть взаимное расположение прямых
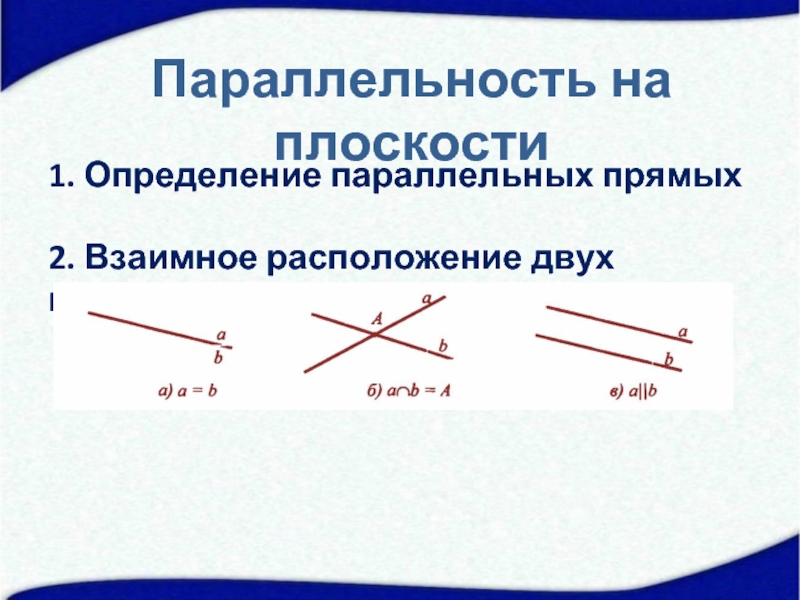
- 3. Параллельность на плоскости 1. Определение параллельных прямых 2. Взаимное расположение двух прямых
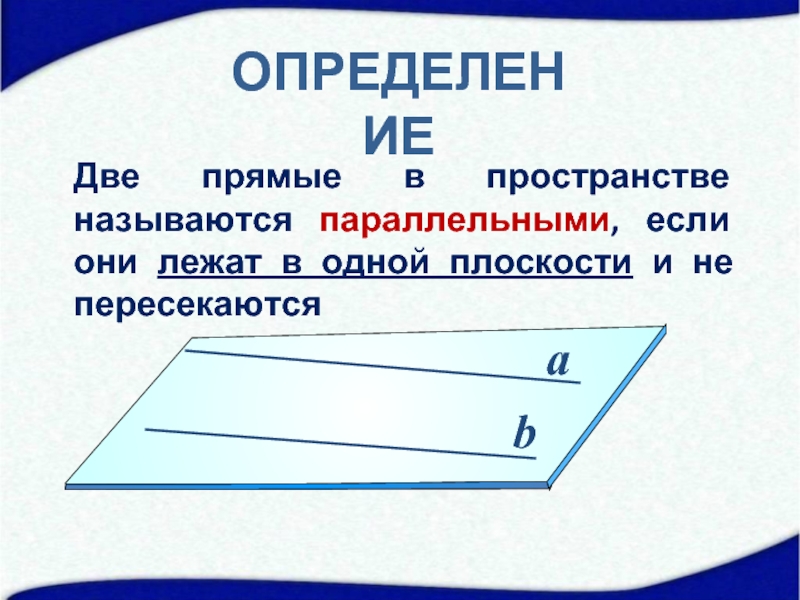
- 4. ОПРЕДЕЛЕНИЕ Две прямые в пространстве называются параллельными,
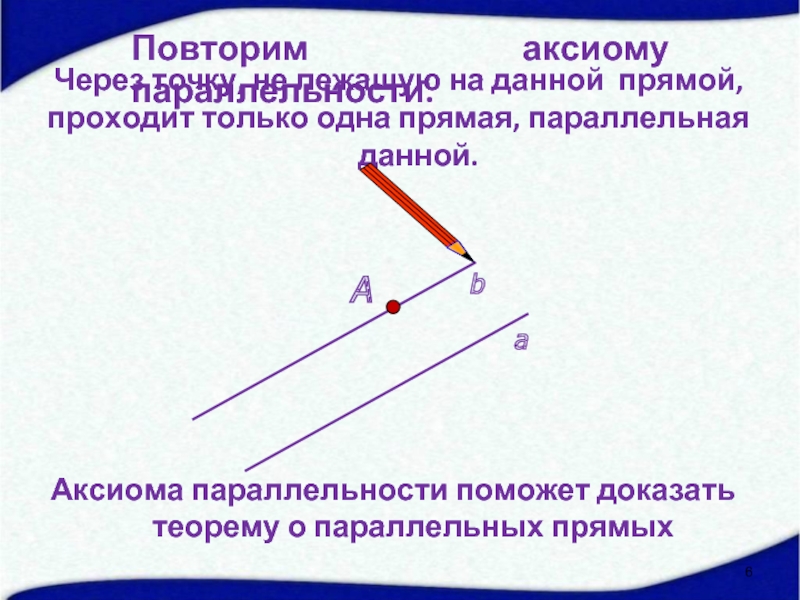
- 6. А Через точку, не лежащую на данной
- 7. ТЕОРЕМА Через любую точку пространства, не лежащую
- 8. М a b 1.
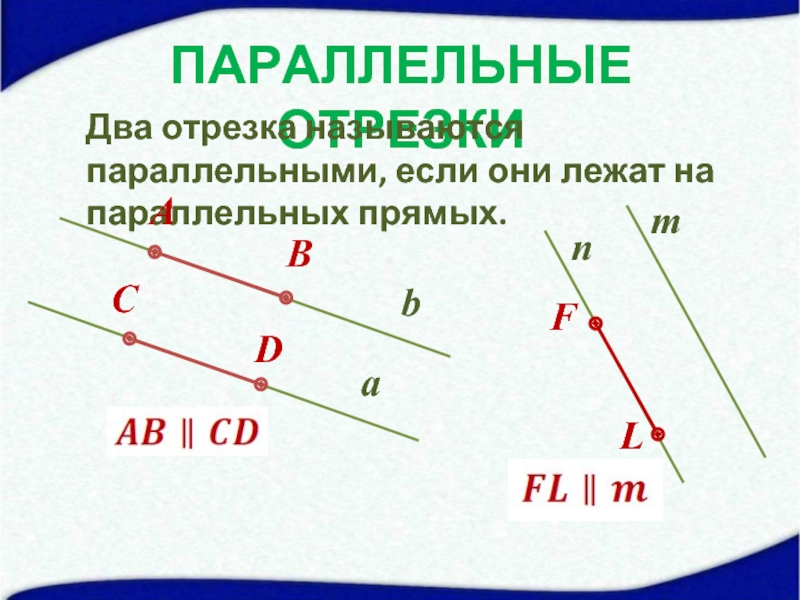
- 9. ПАРАЛЛЕЛЬНЫЕ ОТРЕЗКИ Два отрезка называются параллельными, если
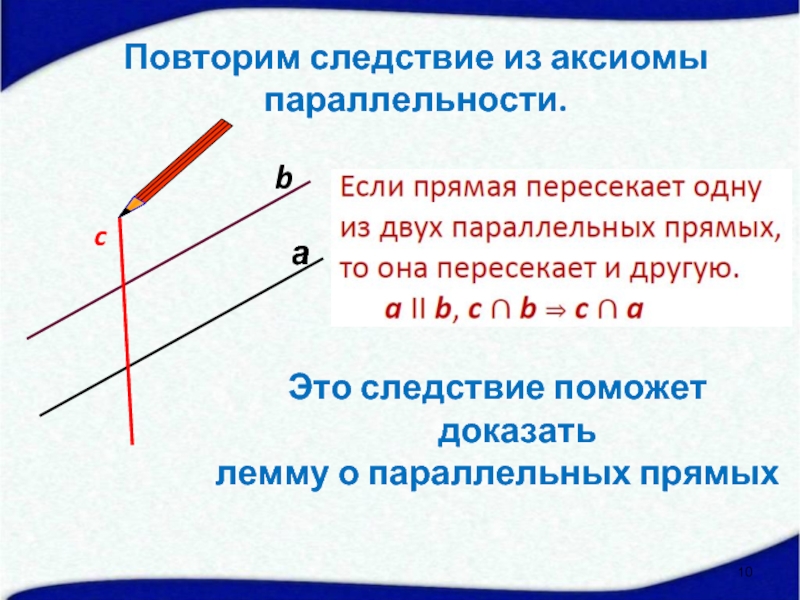
- 10. а c b Это следствие поможет доказать
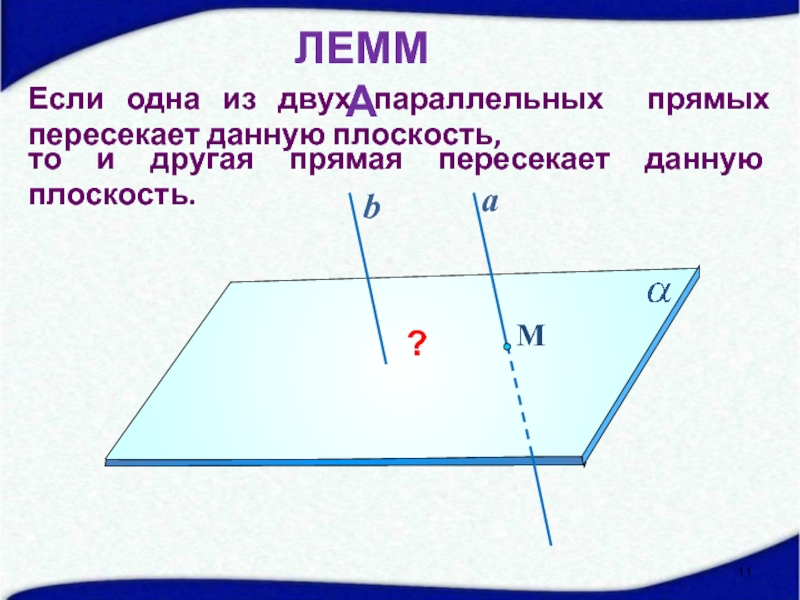
- 11. Если одна из двух параллельных прямых пересекает
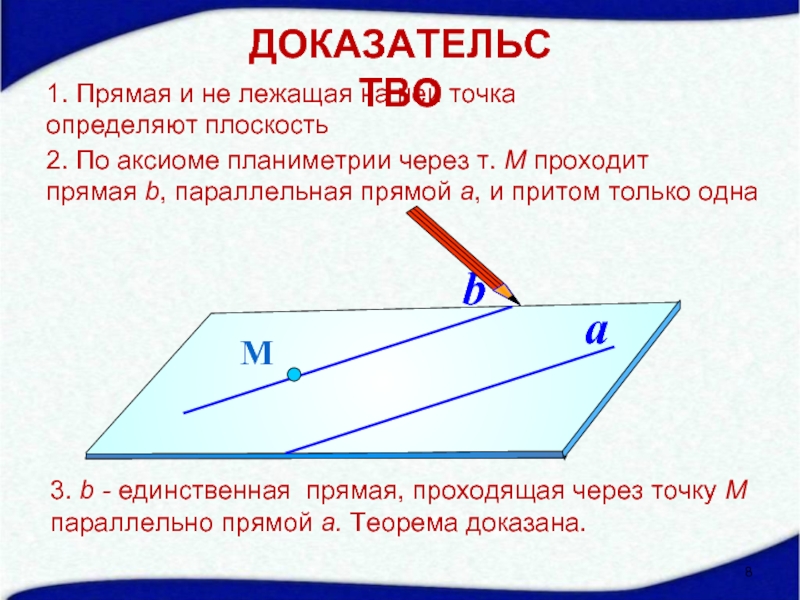
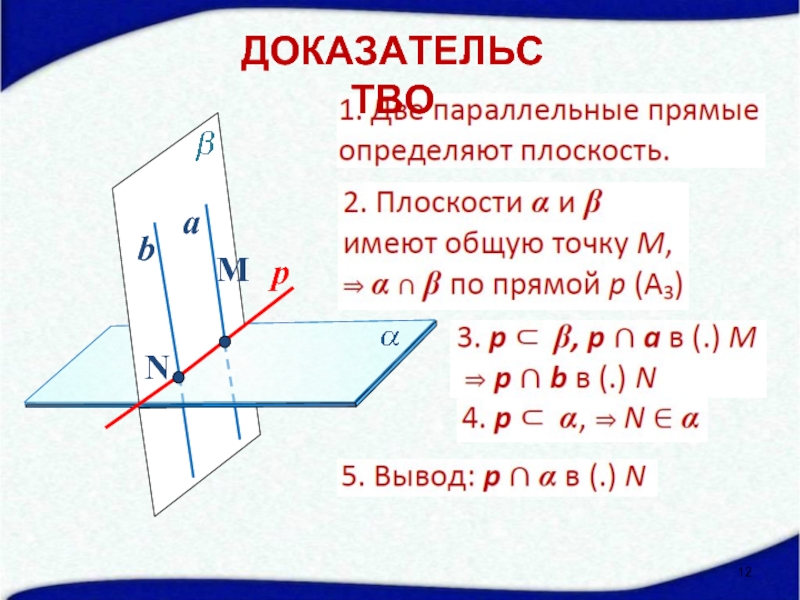
- 12. М a ДОКАЗАТЕЛЬСТВО
- 13. а b с Повторим следствие из аксиомы
- 14. ТЕОРЕМА Если две прямые параллельны третьей, то
- 15. a b с
- 16. Q
- 18. ДОМАШНЕЕ ЗАДАНИЕ П. 4 И 5 УЧИТЬ ТЕОРЕМЫ И ДОКАЗАТЕЛЬСТВА № 16
ЦЕЛИ УРОКА 1. Рассмотреть взаимное расположение прямых в пространстве 2. Доказать теоремы о параллельности прямых 3. Закрепить понятия на моделях куба, и пирамиды
Слайд 2ЦЕЛИ УРОКА
1. Рассмотреть взаимное расположение прямых в пространстве
2. Доказать теоремы о
параллельности прямых
3. Закрепить понятия на моделях куба, и пирамиды
Слайд 3Параллельность на плоскости
1. Определение параллельных прямых
2. Взаимное расположение двух прямых
Слайд 4ОПРЕДЕЛЕНИЕ
Две прямые в пространстве называются параллельными, если они лежат в одной
плоскости и не пересекаются
a
b
Слайд 6А
Через точку, не лежащую на данной прямой,
проходит только одна прямая,
параллельная данной.
а
b
Аксиома параллельности поможет доказать теорему о параллельных прямых
Повторим аксиому параллельности.
Слайд 7ТЕОРЕМА
Через любую точку пространства, не лежащую на данной прямой, проходит прямая,
параллельная данной, и притом только одна.
Слайд 8М
a
b
1. Прямая и не лежащая на ней точка
определяют плоскость
ДОКАЗАТЕЛЬСТВО
2. По
аксиоме планиметрии через т. М проходит
прямая b, параллельная прямой а, и притом только одна
прямая b, параллельная прямой а, и притом только одна
3. b - единственная прямая, проходящая через точку М
параллельно прямой а. Теорема доказана.
Слайд 9ПАРАЛЛЕЛЬНЫЕ ОТРЕЗКИ
Два отрезка называются параллельными, если они лежат на параллельных прямых.
b
a
А
В
D
С
m
n
L
F
Слайд 10а
c
b
Это следствие поможет доказать
лемму о параллельных прямых
Повторим следствие из аксиомы
параллельности.
Слайд 11Если одна из двух параллельных прямых пересекает данную плоскость,
М
a
?
b
ЛЕММА
то и
другая прямая пересекает данную плоскость.
Слайд 13а
b
с
Повторим следствие из аксиомы
параллельности.
Если две прямые параллельны третьей прямой,
то они параллельны.
Аналогичное утверждение имеет место и для трех
прямых в пространстве.
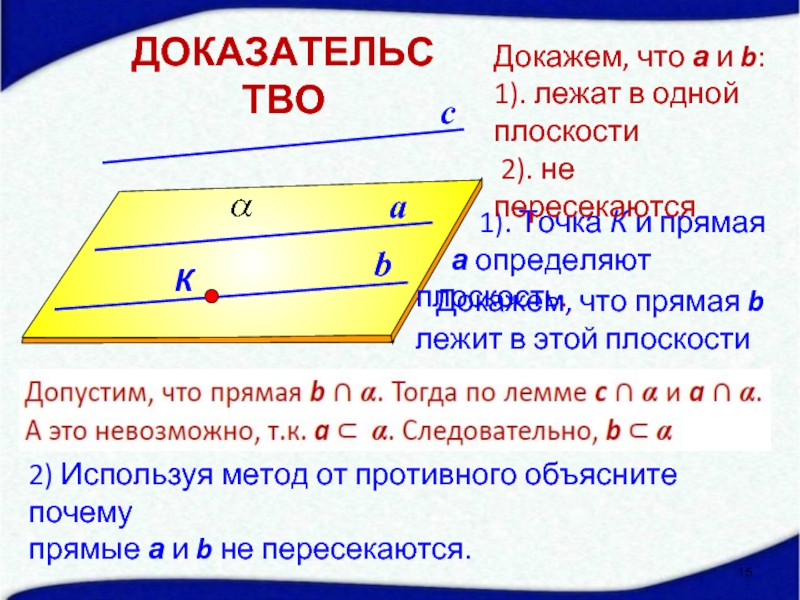
Слайд 15
a
b
с
1). Точка К и прямая
а определяют плоскость.
Докажем, что а и b:
1). лежат в одной
плоскости
2). не пересекаются
2) Используя метод от противного объясните почему
прямые а и b не пересекаются.
Докажем, что прямая b
лежит в этой плоскости
ДОКАЗАТЕЛЬСТВО
