Математические методы в инженерии презентация

полигон, и т.д.);
проверка статистических гипотез;
отсев грубых погрешностей измерений;
оценка истинного значения измеряемой величины;
оценка точности измерения;
Построение эмпирических формул
обработка результатов косвенных измерений;
подбор эмпирических формул;
определение параметров стохастических зависимостей
по выборочным данным;
Анализ и интерпретация результатов исследования
сглаживание и численное дифференцирование;
численное интегрирование;
интерполяция;

МАТЕМАТИЧЕСКИЕ МЕТОДЫ В ИНЖЕНЕРИИ

математические модели.
Пространство элементарных событий.
Операции над событиями.
Вероятность.
Дискретные и непрерывные случайные величины.
Функция распределения и плотность распределения
случайной величины.
Числовые характеристики случайных величин.

Выборочный метод. Общие понятия о генеральной совокупности и выборке.
Эмпирическая функция и плотность распределения и их
графическое изображение (гистограмма, полигон, полигон накопленных частот).
Числовые характеристики выборки: эмпирическое среднее, дисперсия,
размах выборки, коэффициент вариации, стандартное отклонение,
мода, медиана, моменты, асимметрия, эксцесс.

случайные факторы
∙ Пространство элементарных событий , составные события
∙ Операции над событиями (диаграммы Эйлера - Венна)

не произойти событие . Допустим, что эксперимент повторен раз, причем интересующее нас событие наступило раз.
Относительной частотой события называется отношение



Частота является случайной величиной, и в разных сериях из опытов она будет принимать различные значения. Но природа массовых случайных событий такова, что с увеличением числа опытов наблюдается свойство статистической устойчивости частоты. Суть этого свойства состоит в том, что при больших частота принимает значения близкие к некоторому постоянному неслучайному числу , которое и принимается за вероятность случайного события.

Теоретическим обоснованием близости относительной частоты и вероятности случайного события служит теорема Бернулли

СТАТИСТИЧЕСКАЯ УСТОЙЧИВОСТЬ ОТНОСИТЕЛЬНОЙ ЧАСТОТЫ СОБЫТИЯ

Оценка статистической вероятности наступления события после -го опыта

Первая серия опытов

Вторая серия опытов

Третья серия опытов

нулем и единицей

2. Относительная частота невозможного события равна нулю

3. Относительная частота достоверного события равна единице

4. Относительная частота суммы несовместных событий равна сумме
вероятностей этих событий

наступления в данном опыте.
Существует несколько подходов к определению вероятности; это – классическое, статистическое, геометрическое и аксиоматическое определения. Все они дополняют и обобщают друг друга.
Статистической вероятностью события называется число около которого колеблется относительная частота при достаточно большом числе повторных испытаний


Классическое определение. Если число исходов опыта конечно и они образуют полную группу равновозможных несовместных событий, то вероятность определяется как отношение числа элементарных исходов , благоприятствующих наступлению события , к числу всех возможных исходов испытания :



Геометрической вероятностью события называется отношение меры области (длины, площади, объема), благоприятствующей наступлению события, к мере всей области :

ВЕРОЯТНОСТЬ СЛУЧАЙНОГО СОБЫТИЯ

единицей

2. Вероятность невозможного события равна нулю

3. Вероятность достоверного события равна единице

4. Вероятность суммы несовместных событий равна сумме
вероятностей этих событий

5. Вероятности противоположных событий в сумме равны единице

появления в одном опыте) равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло:

Это правило обобщается на случай трех и большего числа событий. Для произвольного числа событий формула имеет вид:

т.е. вероятность каждого следующего по порядку события вычисляется при условии, что все предыдущие события произошли.
Для независимых событий их условные вероятности равны безусловным, и приведенные формулы приобретают простой вид (вероятность произведения независимых событий равна произведению их вероятностей):

вероятностей минус вероятность их произведения:

Эта формула обобщается на случай трех и большего числа событий:

Последняя формула выражает вероятность суммы произвольного числа событий через сумму их вероятностей и вероятности произведений этих событий взятых по два, три и т.д.
Для несовместных событий приведенные формулы приобретают особенно простой вид (вероятность суммы несовместных событий равна сумме их вероятностей):

или иное числовое значение, которое принципиально нельзя предсказать, исходя из условий опыта. Причина изменения случайной величины от испытания к испытанию при неизменном комплексе основных условий кроется в не учитываемых случайных факторах.
Случайные величины могут быть дискретными и непрерывными
Пример. Случайные величины:
(а) число очков, выпадающих при бросании игральной кости;
(б) время безотказной работы электрической лампочки;
(в) число выстрелов до первого попадания в цель;
(г) курсы валют;
(д) рост наугад взятого человека;
(е) число бракованных деталей в партии и т.д.
Дискретной называют случайную величину, возможные значения которой – это отдельные изолированные числа, т.е. между двумя соседними значениями нет других возможных значений. Дискретная случайная величина может принимать конечное или счетное множество значений


Непрерывная случайная величина может принимать любые значения, принадлежащие конечному или бесконечному интервалу ; множество ее возможных значений несчетно

основных понятий теории вероятностей, состоит в следующем:

Случайная величина – это числовая функция, определенная на пространстве элементарных событий , которая каждому элементарному исходу ставит в соответствие число .

Чтобы исчерпывающим образом охарактеризовать случайную величину, нужно, задать множество ее допустимых значений, и указать, как часто, т.е. с какой вероятностью она принимает те или иные эти значения. Иными словами, нужно задать распределение этой случайной величины.

Любое правило (функция, график, таблица), позволяющее находить вероятности всевозможных событий, связанных со случайной величиной (в частности, вероятности отдельных значений случайной величины или множества этих значений), называется законом распределения (или распределением) случайной величины.

это перечень ее возможных значений и соответствующих им вероятностей; он может быть определен формулой

позволяющей вычислить вероятность того, что в результате опыта случайная величина примет значение , или задан таблицей, которая называется рядом распределения

Закон (ряд) распределения случайной величины, принимающей конечное число значений, может быть изображен графически в виде многоугольника (или полигона) распределения, если по горизонтальной оси отложить возможные значения случайной величины, а по вертикальной оси – соответствующие вероятности, и соединить полученные точки ломанной линией.
Функция распределения дискретной случайной величины - ступенчатая функция:

, которая для любого числа определяет вероятность события
, т.е.

Свойства функции распределения:
1. Значения функции распределения принадлежат отрезку :

2. Функция распределения – неубывающая функция, т.е. если , то

3. Функция распределения обращается в ноль на минус бесконечности и равна единице в плюс бесконечности:

4. Вероятность того, что случайная величина примет значение, лежащее в интервале , равно приращению функции распределения на этом интервале:

Вероятность того, что непрерывная случайная величина примет одно определенное, заранее указанное значение, например , равна нулю:

РАСПРЕДЕЛЕНИЕ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

называют функцию - первую производную от функции распределения:



Функцию называют также дифференциальной функцией распределения,
а функцию интегральной функцией распределения.

Дифференциальная и интегральная функции распределения – две равноправные формы закона распределения непрерывной случайной величины; зная одну из них, можно вычислить другую:

)


2. Функция распределения может быть выражена через плотность в виде интеграла с переменным верхним пределом:



3. Условие нормировки (несобственный интеграл от плотности в бесконечных пределах равен единице )



4. Вероятность попадания непрерывной случайной величины в интервал определяется равенством

и плотность распределения , как математические модели случайных величин трудно оценить экспериментально. При решении многих практических задач полная информация о случайной величине (закон распределения) не нужна. В этом случае можно описать случайную величину ограниченным набором (неслучайных) числовых показателей. Минимальный набор включает два показателя: математическое ожидание и дисперсию. Более детальная информация о случайной величине содержится в моментах более высокого порядка. Распределение случайной величины будет полностью заданным, если известны все его моменты.

Наиболее важные числовые характеристики случайных величин, используемые при решении практических задач, можно разделить на три группы:
характеристики положения (математическое ожидание, мода, медиана);
характеристики рассеяния (дисперсия, среднеквадратичное отклонение);
характеристики формы (асимметрия, эксцесс)

определяется равенством

Свойства математического ожидания :

1. Математическое ожидание постоянной величины равно самой постоянной:


2. Постоянный множитель можно выносить за знак математического ожидания:


3. Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых:


4. Математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомножителей:

называется математическое ожидание квадрата ее отклонения от своего математического ожидания:


На практике дисперсию удобно вычислять по формуле («математическое ожидание квадрата минус квадрат математического ожидания»)


Для непрерывной случайной величины формулы для дисперсии могут быть записаны с использованием плотности распределения в виде



Среднеквадратичное отклонение (или стандартное отклонение, или просто стандарт) – квадратный корень (положительное значение) из дисперсии:

можно выносить за знак дисперсии, предварительно возведя его в квадрат:


3. Дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых:


4. Если к случайной величине прибавить константу, то ее дисперсия не изменится:

-квантилем), называется такое значение случайной величины , при котором функция распределения принимает значение, равное , т.е. квантиль - это решение уравнения



Медианой распределения называется квантиль, отвечающий значению т.е.


Из определения следует, что одинаково вероятно, окажется ли случайная величина меньше медианы или больше ее, т.е.


Модой непрерывного распределения называется значение случайной величины, при котором плотность распределения достигает максимума. Если мода единственна, то распределение называется унимодальным; если плотность распределения имеет два или несколько локальных максимумов, то распределение называется бимодальным или полимодальным.

более общего понятия – моментов случайной величины.
Начальным моментом порядка ( -м моментом относительно нуля) называется математическое ожидание -й степени случайной величины:



Начальный момент первого порядка – это математическое ожидание самой случайной величины .
Центральным моментом порядка ( -м моментом относительно математического ожидания) называется математическое ожидание -й степени центрированной случайной величины :



Центральный момент первого порядка всегда равен нулю . Центральный момент второго порядка – это дисперсия .

«скошенность» распределения. Этот безразмерный показатель позволяет сравнивать асимметрию распределений, имеющих различный масштаб. Для симметричного распределения (в частности, для нормального) он равен нулю

Эксцесс распределения вычисляется по формуле



Он характеризует «островершинность» распределения по сравнению с нормальным законом, для которого . При пик более острый,
при - более пологий, чем у нормального распределения.

к обработке наблюдений оказывается возможным благодаря тому, что производство наблюдений (измерений) полностью соответствует основной схеме статистических испытаний, называемой выборочным методом.
Выборочный метод в самой общей форме выглядит следующим образом. Имеется некоторая большая совокупность объектов, называемая генеральной совокупностью. Из этой совокупности извлекается независимо один от другого объектов, которые образуют выборку. Число называется объемом выборки. Эти объекты подвергаются детальному исследованию, по результатам которого требуется описать всю генеральную совокупность или какие-нибудь ее свойства, характеристики.
Интересующий нас признак может быть распределен по генеральной совокупности неравномерно, причем даже характер этой неравномерности может быть не известен. Поэтому не всякая выборка хорошо отражает структуру всей генеральной совокупности.
Выборка называется репрезентативной (представительной), если она достаточно хорошо представляет пропорции генеральной совокупности. Если о генеральной совокупности нет никаких сведений, единственный способ получения представительной выборки состоит в случайном отборе элементов выборки, все прочие способы будут необъективными.

образом колеблются вокруг истинного результата. Это означает, что с истинным результатом связана некоторая случайная величина , и каждое реальное наблюдение дает одно из возможных значений этой величины. Все допустимые значения случайной величины (при данном комплексе условий испытания) образуют генеральную совокупность.

Полученные при наблюдениях значения образуют выборку.
Эта выборка формируется в процессе наблюдений независимо от нашей воли, под действием фактора случайности. Это и позволяет применять для обработки наблюдений основные положения теории вероятностей.

Элементы выборки, записанные в порядке возрастания их значений


называются вариационным рядом .

, определяющая для каждого значения относительную частоту события . Строится она так: для данного числа подсчитывается число выборочных значений , меньших и делится на объем выборки.
- неубывающая функция, ее значения принадлежат отрезку :





В интервале между и функция имеет ступенчатый вид, причем все элементы выборки являются точками разрыва функции; величина скачка в каждой точке разрыва – .
Если объем выборки достаточно велик, то эмпирическое распределение должно быть близко к теоретическому распределению . Обоснование этого факта базируется на теореме Гливенко В. И.: при с вероятностью, равной единице, максимальная разница между функциями и стремиться к нулю, т. е. для любого справедливо равенство

является статистической аппроксимацией теоретической функции ; эта аппроксимация тем точнее, чем больше объем выборки.

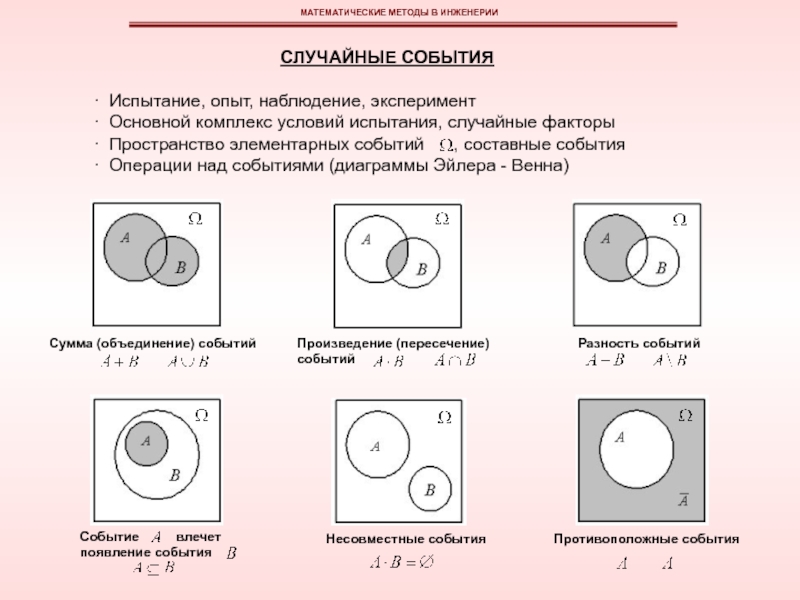
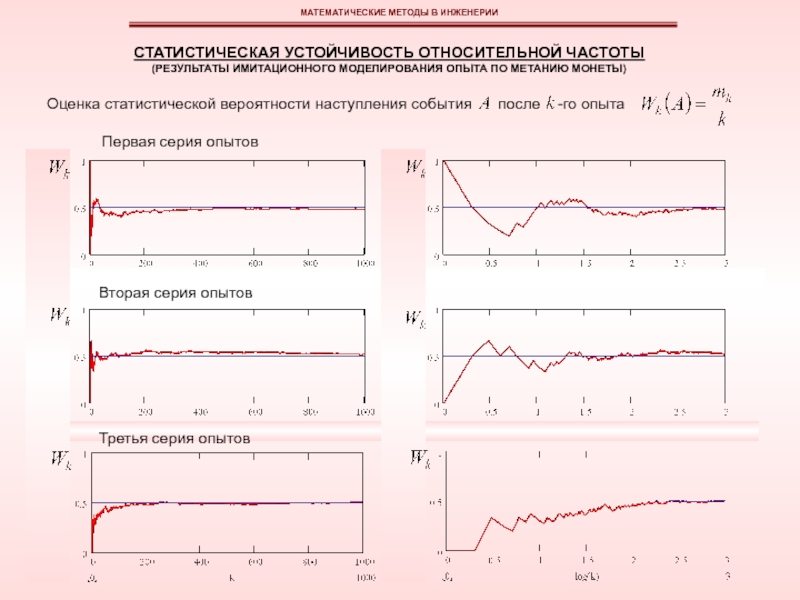
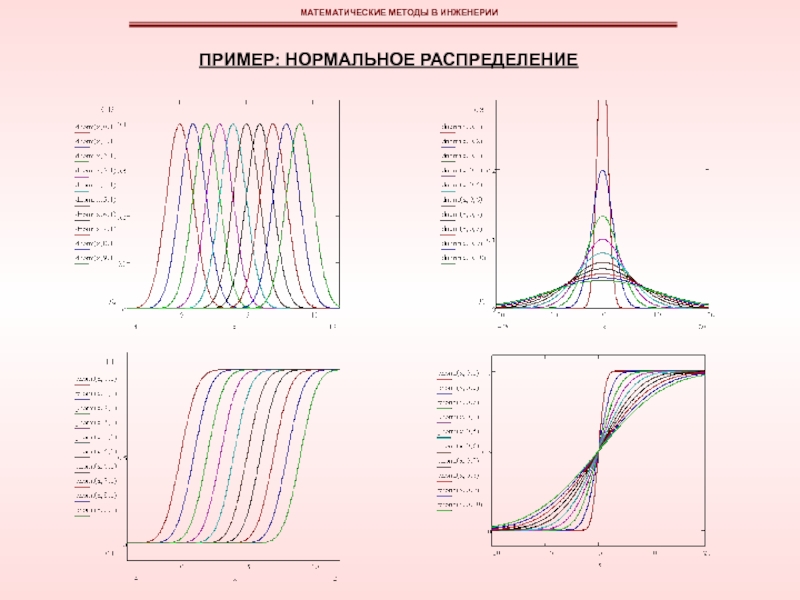
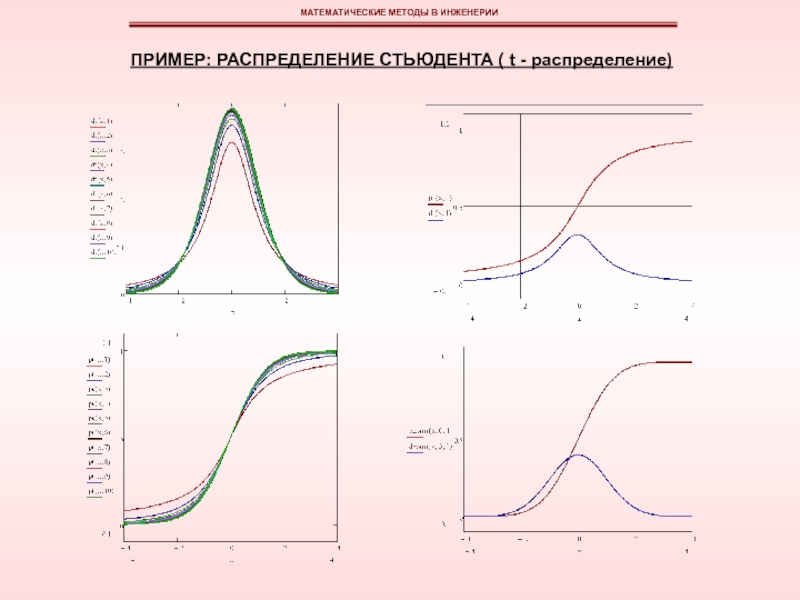
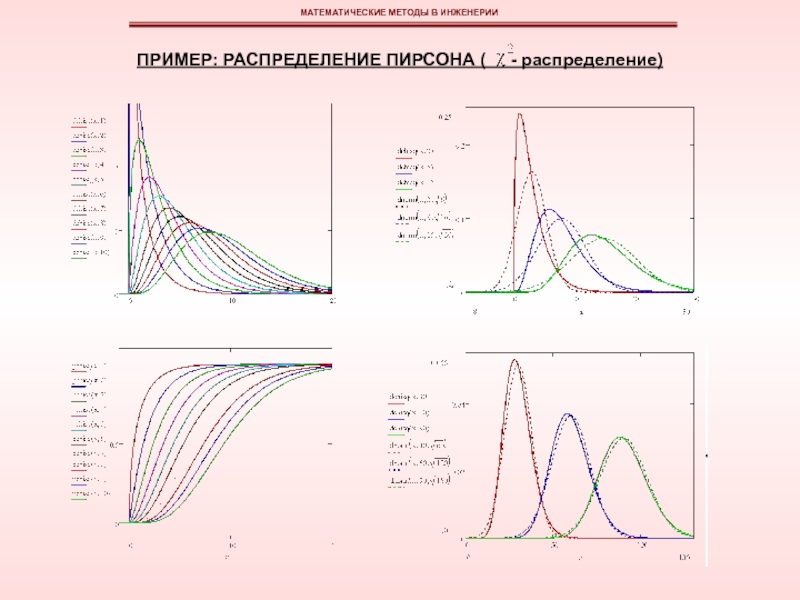
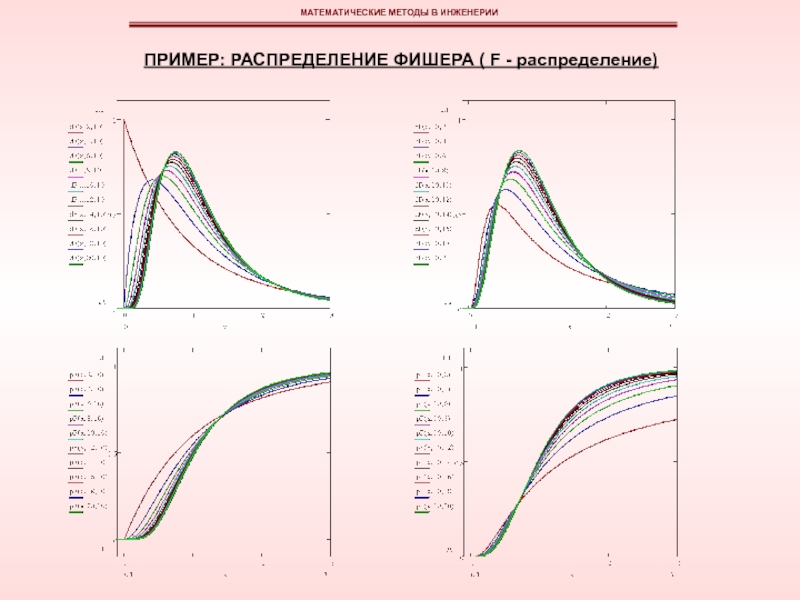
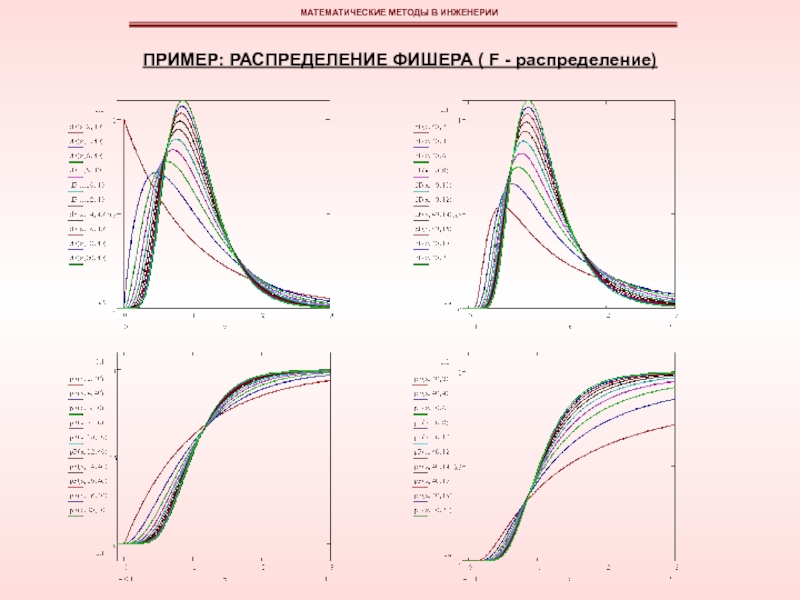
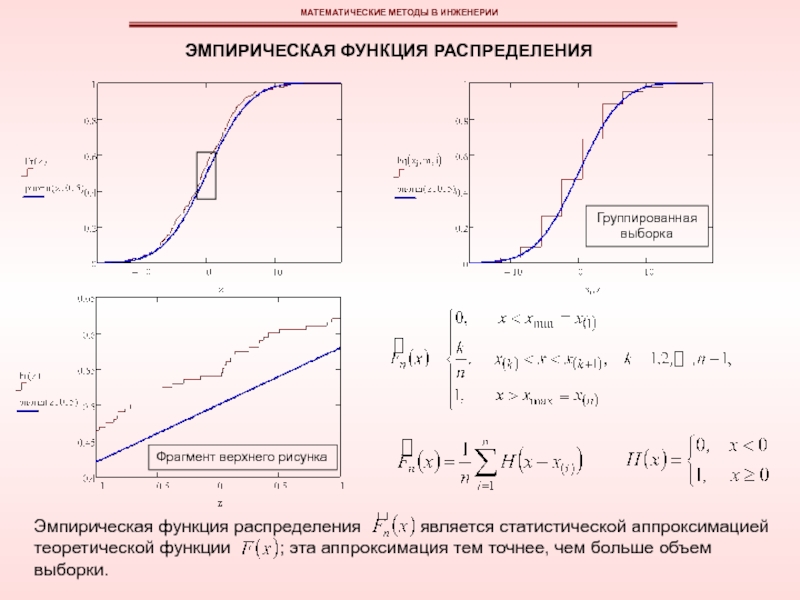
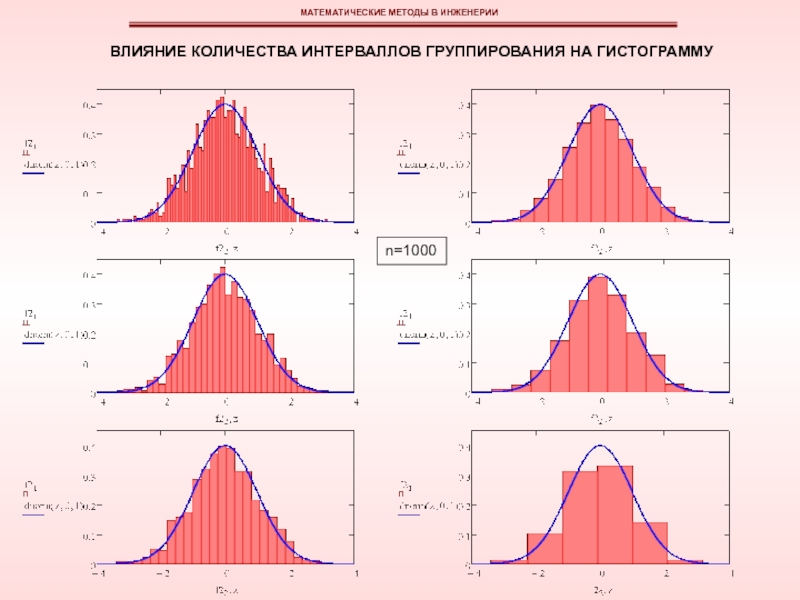
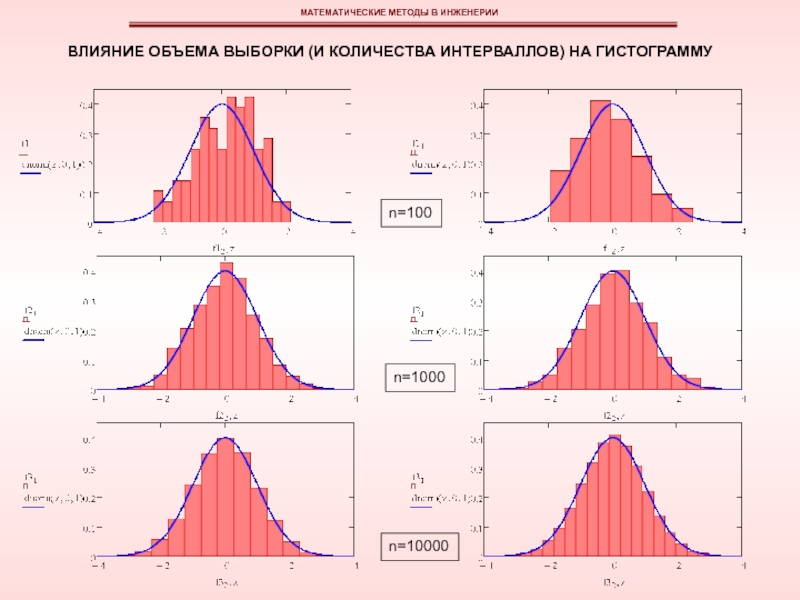
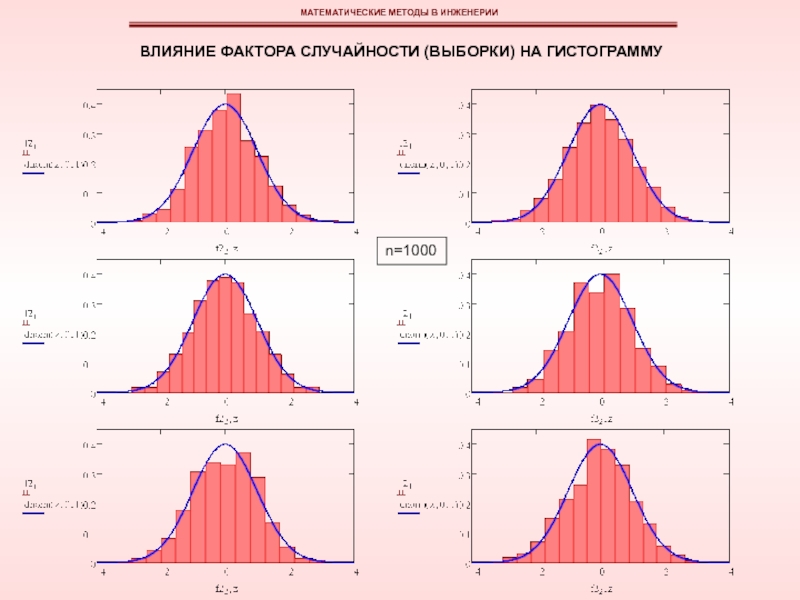
эмпирическая функция плотности вероятностей может быть изображена в виде гистограммы или полигона относительных частот.
С этой целью весь интервал , в котором заключены элементы выборки, разбивается на ряд частичных интервалов длины и подсчитывается частота – количество элементов выборки попавших в -й интервал (и относительная частота ) .
Гистограммой частот называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длины , а высоты равны отношению (плотность частоты). Площадь частичного -го прямоугольника равна -сумме частот элементов, попавших в -й интервал. Площадь гистограммы частот равна объему выборки .
Полигон частот получается при соединении ломаной линией точек
, т. е. середин верхних сторон прямоугольников гистограммы.
Аналогично определяется гистограмма и полигон относительных частот. В этом случае площадь частичного -го прямоугольника равна -относительной частоте элементов, попавших в -й интервал. Площадь гистограммы относительных частот равна сумме всех относительных частот, т. е. единице.
Гистограмма относительных частот (эмпирическая плотность распределения) является статистической аппроксимацией теоретической плотности распределения; эта аппроксимация тем точнее, чем больше объем выборки.

.
Числовые характеристики выборки вычисляются по следующим формулам.
Показатели положения
эмпирическое (выборочное) среднее (несмещенная и состоятельная, а при нормальном законе распределения и эффективная оценка мат. ожидания)


выборочный квантиль уровня - решение уравнения
выборочная медиана – квантиль уровня ½. (состоятельная и несмещенная оценка генерального среднего; оценка не эффективна, ее дисперсия в 1.5 раз больше дисперсии среднего ). При нечетном объеме выборки медиана – это средний элемент вариационного ряда, при четном – полусумма двух средних элементов.
минимальный и максимальный элементы выборки


мода – элемент выборки с наибольшим числом повторений (если в выборке многие элементы повторяются).

- смещенная, - несмещенная) оценка генеральной дисперсии



эмпирический стандарт (среднеквадратичное отклонение)



размах выборки (при среднем объеме выборки ( ) справедливо приближенное соотношение )

выборочный коэффициент вариации (относительное рассеивание случайной
величины)

С помощью удобно сравнивать различные случайные величины (выборки); коэффициент вариации показывает насколько велико рассеивание по сравнению со средним значением случайной величины.

(состоятельная, смещенная оценка)



выборочный эксцесс (состоятельная, смещенная оценка)



Несмещенные оценки коэффициентов асимметрии и эксцесса вычисляются по формулам:

неизвестных параметров следует приравнять теоретические моменты соответствующим эмпирическим моментам того же порядка. Приравнивая первые начальные моменты и вторые центральные моменты ,
получим оценки математического ожидания и дисперсии:


Метод наибольшего правдоподобия. Пусть задана выборка
объема из генеральной совокупности, плотность распределения которой зависит от неизвестного параметра . Значение этого параметра нужно оценить по выборке. Функцией правдоподобия называется функция параметра , определяемая соотношением

В качестве оценки параметра берется значение, при котором функция правдоподобия достигает максимума. Из решения уравнения


определяется функция выборки , которая называется наиболее правдоподобной оценкой параметра . Если существует эффективная оценка, она получается методом наибольшего правдоподобия.

статистики для технических приложений. – М.: Наука, 1965.
2. Пустыльник Е.И. Статистические методы анализа и обработки наблюдений. – М.: Наука, 1968.
3. Румшиский Л.З. Математическая обработка результатов эксперимента. – М.: Наука, 1971.
4. Львовский Е.Н. Статистические методы построения эмпирических формул. – М.: Высшая школа, 1982.
5. Гутер Р.С., Овчинский Б.В. Элементы численного анализа и математической обработки результатов опыта. - М.: Наука, 1970.
6. Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров. – М.: Высшая школа, 1994.
7. Плис А.И., Сливина Н.А. Mathcad 2000. Математический практикум для экономистов и инженеров. – М.: Финансы и статистика, 2000.
8. Ивановский Р.И. Компьютерные технологии в науке и образовании. Практика применения систем MathCAD Pro. - М.: Высшая школа, 2003.

и технике. – М.: Наука, 1977.
10. Щиголев Б.М.Математическая обработка наблюдений. – М.: Наука, 1969.
11. Вентцель Е.С. Теория вероятностей. – М.: Изд. центр «Академия», 2005.
12. Лагутин М.Б. Наглядная математическая статистика. М.: БИНОМ, 2007 .
13. Хан Г., Шапиро С. Статистические модели в инженерных задачах. – М.: Мир, 1969.
14. Линник Ю.В. Метод наименьших квадратов и основы теории обработки наблюдений. – М.: Физматгиз, 1962.
15. Кобзарь А.И. Прикладная математическая статистика. Для инженеров и научных работников. – М.: Физматлит, 2006 .
16. Кибзун А.И., Горяинова Е.Р., Наумов А.В. Теория вероятностей и математическая статистика. Базовый курс с примерами и задачами. – М.: Физматлит, 2005.
17. Крянев А.В., Лукин Г.В. Математические методы обработки неопределенных данных. – М.: Физматлит, 2006.
18. Чистяков В.П. Курс теории вероятностей. – М.: Дрофа, 2007.
19. Дрейпер Н., Смит Г. Прикладной регрессионный анализ. - М.: Изд. дом «Вильямс», 2007.
20. Зайдель А.Н. Ошибки измерений физических величин. – СПб.: Лань, 2005.
21. Протасов К.В. Статистический анализ экспериментальных данных. – М. Мир, 2005.
22. Калиткин Н. Н. Численные методы. – М.: Наука, 1978.
23. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. – М.: Наука, 1987.
24. Самарский А.А., Гулин А.В. Численные методы. – М.: Наука, 1989.

величине, чтобы описать ее математически? (минимальный набор числовых характеристик и полное, исчерпывающее описание).
Как связаны между собой понятия функции распределения и плотности распределения (вероятностей) непрерывной случайной величины?
Сформулируйте основные свойства функции распределения случайной величины.
Сформулируйте основные свойства плотности распределения вероятностей случайной величины.
Как вычисляются характеристики центра распределения – математическое ожидание, медиана мода? Как они соотносятся между собой? Проиллюстрируйте ответ графически (схематично).
Сформулируйте основные свойства математического ожидания случайной величины.
Что такое моменты случайной величины? Дайте соответствующие определения. Моменты какого порядка обычно используются в статистических расчетах?
Как определяются математическое ожидание и дисперсия произвольной функции случайного аргумента?
Сформулируйте основные свойства дисперсии случайной величины.
Что такое выборочный статистический метод? Как он соотносится с результатами экспериментальных измерений?
Что такое генеральная совокупность и выборка применительно к результатам измерений?
Как строится эмпирическая функция распределения? Сформулируйте теорему, гарантирующую близость эмпирической и теоретической функций распределения?
Как строится гистограмма и полигон частот (относительных частот)? С какой целью прибегают к построению этих графиков?
Какие методы получения точечных оценок Вы знаете?
Какие числовые характеристики выборки относятся к показателям положения, формы, разброса?

Литература: [1], [2], [9] - [18].