- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математические идеи в почвоведении. Методы статистического анализа данных. (Лекция 1) презентация
Содержание
- 1. Математические идеи в почвоведении. Методы статистического анализа данных. (Лекция 1)
- 2. ЦЕЛЬ КУРСА : овладение современными методами статистического
- 3. МЕСТО КУРСА В ПРОФЕССИОНАЛЬНОЙ ПОДГОТОВКЕ ВЫПУСКНИКОВ
- 4. Курс «Математические методы в почвоведении» проводится в
- 5. ТРЕБОВАНИЯ К УРОВНЮ УСВОЕНИЯ СОДЕРЖАНИЯ КУРСА:
- 6. СПИСОК РЕКОМЕНДОВАННОЙ ЛИТЕРАТУРЫ Владимирский Б.М.
- 7. План лекции: 1. Развитие математических
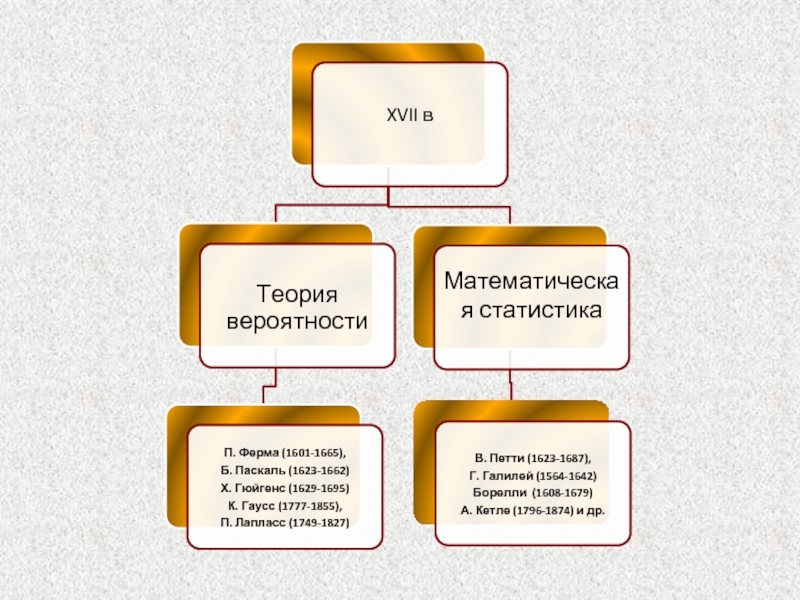
- 8. Развитие математических идей в биологии и почвоведении
- 9. В глубокой древности, с образованием государств
- 11. Адольф Кетле (22.02.1796 – 17.12.1874) Формирование статистики
- 12. Ф. Гальтон (1822-1911) Английский ученый основатель школы
- 13. Карл Пирсон (1857-1936) Пирсон считается одним
- 14. В. Госсет - «Стьюдент» (1876-1937) Открыл
- 15. Р.Э. Фишер (1890-1962) Работал научным сотрудником
- 16. Первые опыты по использованию статистических
- 17. До конца 50-х начала
- 18. Интенсивное внедрение статистических методов
- 19. Понятие генеральной совокупности и случайной выборки.
- 20. Испытание осуществление какого-нибудь определенного комплекса условий,
- 21. Величины, в процессе испытаний не меняющие своих
- 22. Если в некотором интервале переменная может принимать
- 23. Явления, происходящие в результате испытаний, в
- 24. Совокупность из которой отбирается некоторая часть ее
- 25. Часть генеральной совокупности отобранная тем или иным
- 26. Выборочный метод является основным при изучении статистических
- 27. Выборка должна быть представительной – репрезентативной
- 28. Рендомизация (от англ. random - случай) –
- 29. Способы отбора вариант из генеральной совокупности: Повторный
- 30. Виды отбора единиц из генеральной совокупности: Типический (или групповой); Серийный (или гнездовой); Механический.
- 31. Шкалы измерений: Именная (или классификационная); Порядковая шкала; Интервальная шкала; Шкала отношений.
- 32. Классификация признаков: Качественные Признаки, поддающиеся измерению на
- 33. Ели в основе классификации лежит группировка данных, то признаки делят на: Альтернативные; Порядковые; Ранговые.
- 34. Общей основой классификации признаков являются мера и
- 35. Процесс систематизации или упорядочения, первичных биометрических данных
- 36. Статистические ряды: Атрибутивные Вариационные Динамики Временные
- 37. Вариационным рядом называется ряд чисел, показывающий закономерность
- 38. Двойной ряд чисел, показывающий, каким образом числовые
- 39. Числа, показывающие, сколько раз отдельные варианты встречаются
- 40. Графическое представление экспериментальных данных: гистограммы, полигоны, кривые
- 41. Кривая распределения Линейный график,
- 42. Полигон распределения частот При построении графика
- 43. Полигон распределения частот: по оси абсцисс откладывают
- 44. Гистограмма распределения частот При построении графика
- 45. Эмпирический ряд распределения можно изобразить в
- 46. классы Накопленные частоты Кумулята получается,
- 47. Диаграмма «Ящик с усами» Результаты выборочных
- 48. Круговая диаграмма Термин "круговые диаграммы" впервые
- 49. Стьюдент из книги: Ермолаев О. Ю. «Математическая
- 50. Благодарю за внимание!
Слайд 2ЦЕЛЬ КУРСА :
овладение современными методами статистического анализа данных, получаемых в результате
В процессе освоения курса студент должен овладеть умением применять результаты статистического анализа для интерпретации полученных данных и делать содержательные выводы.
Слайд 3МЕСТО КУРСА В ПРОФЕССИОНАЛЬНОЙ ПОДГОТОВКЕ ВЫПУСКНИКОВ
Программа курса «Математические методы в почвоведении»
Слайд 4Курс «Математические методы в почвоведении» проводится в 4 семестре подготовки специалистов,
Слайд 5ТРЕБОВАНИЯ К УРОВНЮ УСВОЕНИЯ СОДЕРЖАНИЯ КУРСА:
Студент должен свободно ориентироваться в выборе
Слайд 6СПИСОК РЕКОМЕНДОВАННОЙ ЛИТЕРАТУРЫ
Владимирский Б.М. Математические методы в биологии. Ростов-на-Дону: РГУ,
Владимирский Б.М. Горстко А.Б., Ерусалимский Я.М. Математика. Общий курс. СПб.: Изд-во «Лань», 2002. – 960 с.
Дмитриев Е.А. Математическая статистика в почвоведении. М.: Изд-во Моск. ун-та, 1972 - 292 с.
Доспехов Б.А. Методика полевого опыта. М. Колос, 1968. -336 с.
Дюк В. Обработка данных на ПК в примерах. Санкт-Петербург: Питер, 1997. -240 с.
Дюран Б., Одел П. Кластерный анализ. М.: Статистика. 1997. - 128 с.
Лакин Г.Ф. Биометрия. М.: высшая школа, 1990. – 352 с.
Лебедева Н.В., Дроздов Н.Н., Криволуцкий Д.А. Биоразнообразие и его оценка. М.: МГУ, 1999. – 99 с.
Лебедева Н.В., Рыбянец Т.В. Математические методы в почвоведении. Задачи с методическими указаниями. Ростов-на-Дону: Биос, 2002. – 66 с.
Лоули Д. Максвел Л. Факториальный анализ как статистический метод. М.: Мир. 1967. - 144 с.
Применение методов математической статистики в почвоведении, мелиорации и сельском хозяйстве. Москва-Новочеркасск. – 1980. – 57 с.
Рожков В.А. Почвенная информатика. М.: Агропромиздат, 1989. – 221 с.
Рокицкий П.Ф. Биологическая статистика. Минск: Вышэйш. Школа, 1967. 328 с.
Справочник по прикладной статистике/ Под ред. Э.Ллойда, У. Ледермана, Ю.Н. Тюрина. Т. 1,2. М.: Финансы и статистика. 1989, 1990. 510 с., 526 с.
Слайд 7
План лекции:
1. Развитие математических идей в биологии и почвоведении.
2. Понятие генеральной
3. Графическое представление экспериментальных данных.
Слайд 8Развитие математических идей в биологии и почвоведении
Применение математического аппарата в исследованиях
Слайд 9
В глубокой древности, с образованием государств возникла необходимость в учете населения,
Такие сведения еще за несколько тысячелетий до н.э. собирались в Китае, Египте, Древнем Риме. В Средние века эпизодически проводились переписи населения, домашнего имущества, земельных угодий; велся учет лиц, пригодных к военной службе.
С развитием торговли и международных товаро-денежных отношений все более расширялся круг учитываемых явлений и собираемых о них сведений. Стали собираться данные о ввозимой продукции, ценах на товары и т.д.
Слайд 11Адольф Кетле (22.02.1796 – 17.12.1874)
Формирование статистики в научную дисциплину связано с
Одним из первых показал, что случайности наблюдаемые в живой природе вследствие их повторяемости, обнаруживают тенденцию, следуя определенной закономерности, некоторую можно исследовать и описать точным и математическими методами.
Труды:
1835 «О человеке и развитии его способностей, или Опыт социальной физики»
1848 «О социальной системе и законах, управляющих ею»
1871 «Антропология»
Совместно с ведущими математиками своего времени А. Кетле организовал так называемую Центральную статистическую комиссию, пропагандировавшую важность проведения серьезных статистических исследований.
С именем Кетле в истории науки связан переход социальной статистики от сбора и количественного описания данных к установлению постоянных корреляций показателей, или статистических закономерностей. Выявленные им с помощью математического вероятностного анализа постоянные соотношения показателей Кетле трактовал как объективные социальные законы.
Слайд 12Ф. Гальтон (1822-1911)
Английский ученый основатель школы биометриков.
Впервые применил статистический метод
Разработал методику регрессионного и корреляционного анализа.
Создал основной математический аппарат биометрии.
Слайд 13Карл Пирсон (1857-1936)
Пирсон считается одним из основателей статистики. В молодости у
Его интерес сформировался под влиянием эволюционной теории Дарвина, которую он хотел проверить с помощью различных методов.
Вместе с такими философами, как Юм и Мах, Пирсон разделял взгляды на причинность как сопряженную вариацию ("корреляция").
Ободренный сэром Фрэнсисом Гальтоном и Уолтером Велдоном, он предложил математическую формулировку идеи корреляции, о которой размышлял и сам Гальтон. Результатом явился широко известный коэффициент корреляции Пирсона.
С именем Пирснона связано понятие среднего квадратического отклонения, обоснование метода хи-квадрат. Он развил теорию линейной и нелинейной корреляции, разработал методику построения множественной регрессии.
Совместно с Гальтоном и Уэльдоном основал в 1901 г выпуск журнала «Биометрика».
Слайд 14В. Госсет - «Стьюдент»
(1876-1937)
Открыл закон распределения выборочных средних в зависимости от
Описанный закон распределения оказался применим к выборкам любого размера.
Критерий Стьюдента направлен на оценку различий величин средний значений двух выборок, которые распределены по нормальному закону.
Одним из главных достоинств критерия является широта его применения. Он может быть использован для сопоставления средних у связных и несвязных выборок, причем выборки могут быть не равны по величине.
t-критерий был разработан Уильямом Госсетом (1876-1937) для оценки качества пива на пивоваренных заводах Гиннесса в Дублине (Ирландия).
В связи с обязательствами перед компанией по неразглашению коммерческой тайны (руководство Гиннесса считало таковой использование статистического аппарата в своей работе), статья Госсета вышла в 1908 году в журнале «Биометрика» под псевдонимом «Student» (Студент).
Слайд 15Р.Э. Фишер (1890-1962)
Работал научным сотрудником Ротамстедской сельскохозяйственной опытной станции, а
Ввел науку такие понятия как: «варианса», «число степеней свободы», «даты».
Заложил основы теории планирования эксперимента.
Разработал метод комплексной оценки действия факторов и их возможных сочетаний на результативный признак – метод основанный на разложении дисперсии, получивший название дисперсионного анализа.
Слайд 16
Первые опыты по использованию статистических методов в почвоведении относятся к 20-м
Этому немало способствовало появление литературы по математической статистике прикладного характера (Голубев, 1920; Сапегин, 1922; Филиппченко, 1926; Поморский, 1927 и др.).
Слайд 17
До конца 50-х начала 60-х гг. статистические методы использовались очень скромно,
Слайд 18
Интенсивное внедрение статистических методов в почвоведение, было инициировано и подготовлено работами
(Немчинов, 1945; Перегудов и др., 1948; Федоров, 1957; Финни, 1957; Фишер, 1958; Снедекор, 1961; и др.).
Слайд 19 Понятие генеральной совокупности и случайной выборки.
Признаки: качественные и количественные
Выборочные распределения.
Слайд 20 Испытание осуществление какого-нибудь определенного комплекса условий, который может быть воспроизведен
Под комплексом условий понимают определенную методику выделения объекта изучения, способ его опробования и получение конечного результата измерений.
Слайд 21Величины, в процессе испытаний не меняющие своих значений, называются постоянными.
Если величина
Слайд 22Если в некотором интервале переменная может принимать любые значения (содержит все
Дискретная переменная может принимать лишь некоторые значения, разделенные промежутками.
Слайд 23
Явления, происходящие в результате испытаний, в математической статистике и теории вероятности
Переменная величина, значение которой до проведения испытаний заранее не может быть точно предсказано называется случайной величиной.
Слайд 24Совокупность из которой отбирается некоторая часть ее членов для совместного изучения
N – объем генеральной совокупности:
N →∞
Слайд 25Часть генеральной совокупности отобранная тем или иным способом называется выборочной совокупностью
n – объем выборки:
n≥2
Слайд 26Выборочный метод является основным при изучении статистических совокупностей.
Преимущества:
- сокращает время и
- позволяет получать информацию о таких совокупностях сплошное обследование которых практически невозможно или не целесообразно.
Слайд 27
Выборка должна быть представительной – репрезентативной (от лат. represento –представляю), т.е.
Слайд 28Рендомизация (от англ. random - случай) – случайный отбор вариант из
Слайд 29Способы отбора вариант из генеральной совокупности:
Повторный
возвращение учтенных единиц в генеральную совокупность
Бесповторный
учтенные
Слайд 30Виды отбора единиц из генеральной совокупности:
Типический (или групповой);
Серийный (или гнездовой);
Механический.
Слайд 31Шкалы измерений:
Именная (или классификационная);
Порядковая шкала;
Интервальная шкала;
Шкала отношений.
Слайд 32Классификация признаков:
Качественные
Признаки, поддающиеся измерению на именных шкалах
Количественные
Признаки, которые могут быть ранжированы
Порядковые
Признаки, поддающиеся количественной оценке
Слайд 33Ели в основе классификации лежит группировка данных, то признаки делят на:
Альтернативные;
Порядковые;
Ранговые.
Слайд 34Общей основой классификации признаков являются мера и счет, в зависимости от
Признаки
Счетные или меристические
мерные
или метрические
Непрерывные
(могут принимать любые числовые значения в пределах: от-до)
Дискретные
(их значения всегда выражаются только целыми числами)
Слайд 35Процесс систематизации или упорядочения, первичных биометрических данных в целях извлечения заключенной
Группировка по одному признаку называется простой (простая таблица), по нескольким признакам - сложной (корреляционная таблица).
Слайд 37Вариационным рядом называется ряд чисел, показывающий закономерность распределения единиц изучаемой совокупности
Слайд 38Двойной ряд чисел, показывающий, каким образом числовые значения признака (хi) связаны
Слайд 39Числа, показывающие, сколько раз отдельные варианты встречаются в данной совокупности называются
Σp=n, где:
Σ- суммирование частот вариационного ряда;
n – объем выборочной совокупности.
Слайд 40Графическое представление экспериментальных данных: гистограммы, полигоны, кривые накопленных частот, ящики с
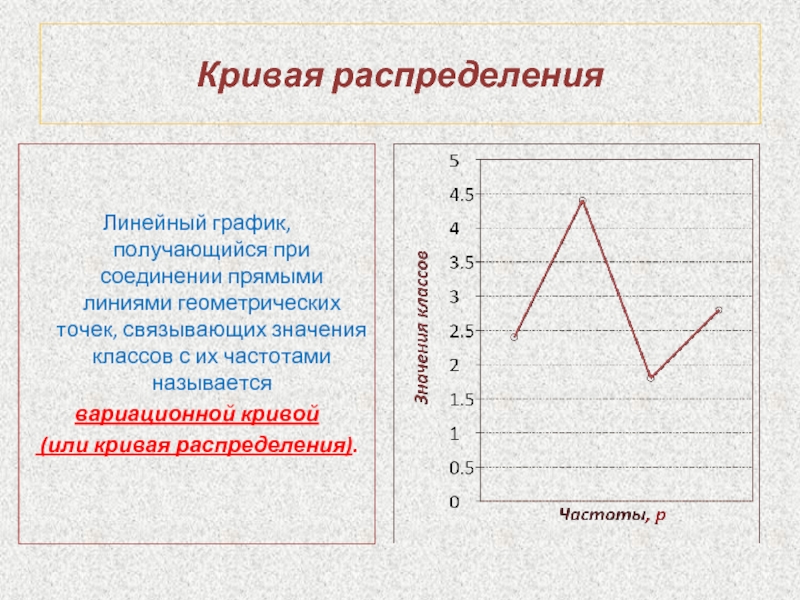
Слайд 41Кривая распределения
Линейный график, получающийся при соединении прямыми линиями геометрических точек,
вариационной кривой
(или кривая распределения).
Слайд 42Полигон распределения частот
При построении графика безинтервального вариационного ряда по оси
Высота перпендикуляров, восстановленных по оси абсцисс соответствует частотам классов. Соединяя вершины перпендикулярными линиями получаем полигон распределения частот.
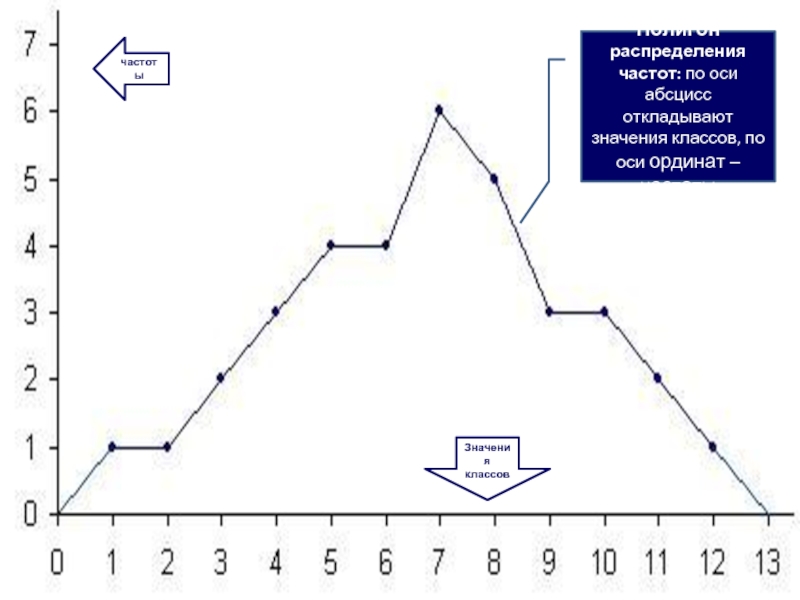
Слайд 43Полигон распределения частот: по оси абсцисс откладывают значения классов, по оси
частоты
Значения классов
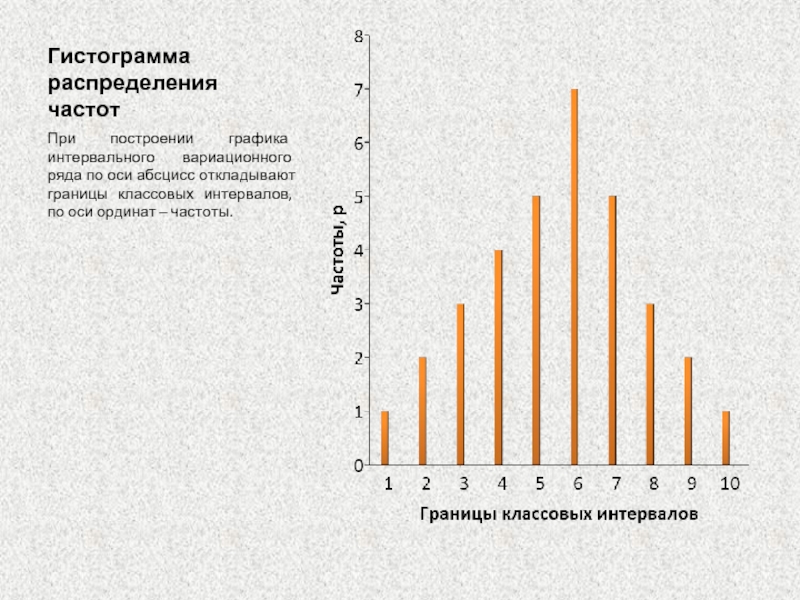
Слайд 44Гистограмма распределения частот
При построении графика интервального вариационного ряда по оси
Слайд 45
Эмпирический ряд распределения можно изобразить в виде кумуляты или огивы.
Накопленные частоты
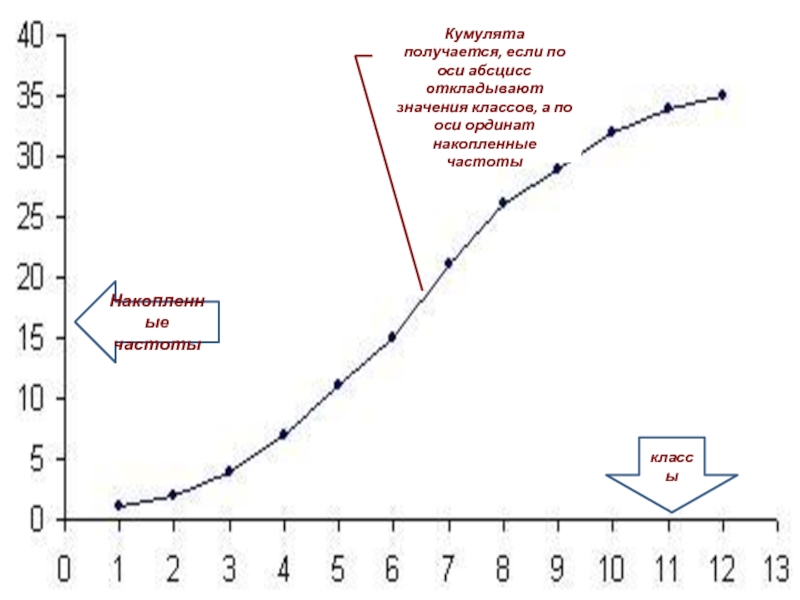
Кумулята получается, если по оси абсцисс откладывают значения классов, а по оси ординат накопленные частоты.
Огива. Если накопленные частоты откладывают по оси абсцисс, а значения классов по оси ординат.
Слайд 46
классы
Накопленные частоты
Кумулята получается, если по оси абсцисс откладывают значения классов, а
Слайд 47Диаграмма «Ящик с усами»
Результаты выборочных наблюдений могут быть представлены в
На диаграммах размаха этого типа вокруг средней точки (т.е. среднего или медианы) рисуются прямоугольник, представляющий выбранный диапазон (т.е. стандартную ошибку, стандартное отклонение, минимум-максимум или константу), и отрезок, также отражающий выбранный диапазон, концы которого расположены вне прямоугольника (см. следующий рисунок).
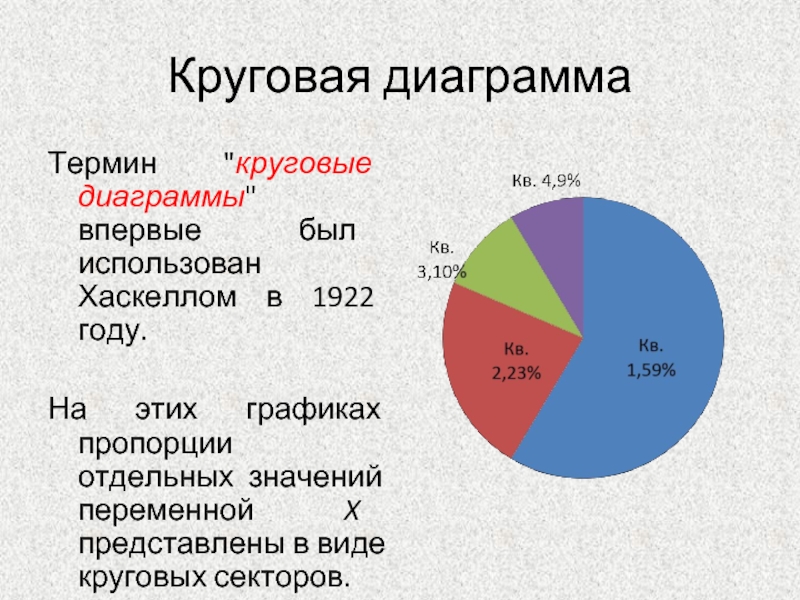
Слайд 48Круговая диаграмма
Термин "круговые диаграммы" впервые был использован Хаскеллом в 1922
На этих графиках пропорции отдельных значений переменной X представлены в виде круговых секторов.