статистической информации для получения науч-ных и практических выводов.
Теоретической основой математической статистики являются законы распределения и
предельные теоремы закона больших чисел.
ВЫБОРОЧНЫЙ МЕТОД
Определение 1. Вся совокупность единиц,









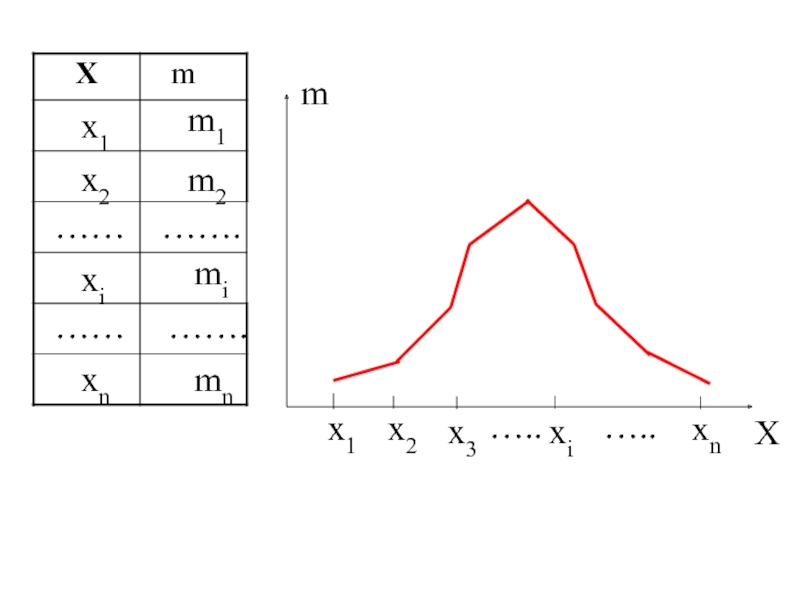
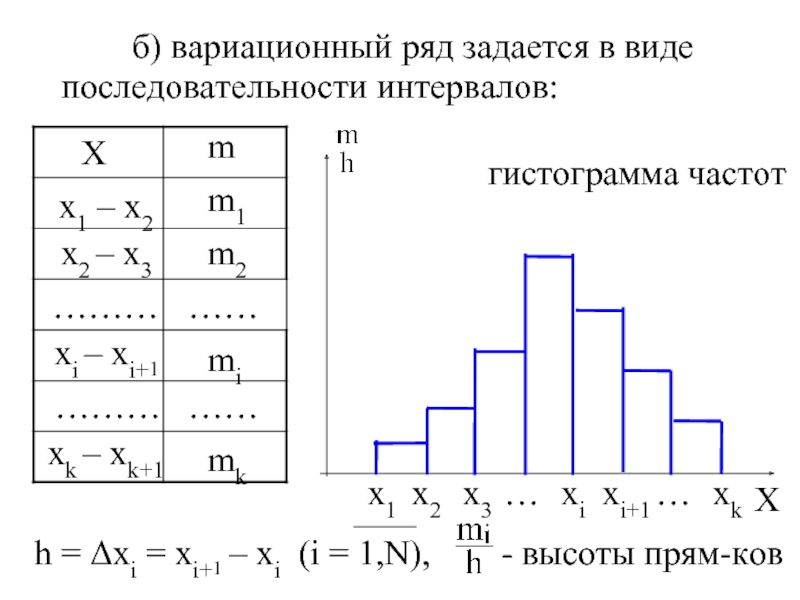
![Определение[ВТ1]. Значения признака Х: х1, х2,…, …, хn называются вариантами, а упорядоченная последовательность](/img/tmb/2/195992/0c4a1814fc9deea76dd3f433e8b83846-800x.jpg)
![Определение[ВТ1]. Соответствие между вариаци- онным и частотным рядами назыв. статистическим распределением выборки.](/img/tmb/2/195992/ce8fbe849876cf6a669d97a63f43e6a0-800x.jpg)