- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Зеркальная симметрия презентация
Содержание
- 1. Зеркальная симметрия
- 2. Симметрия - это гармония в расположении одинаковых предметов
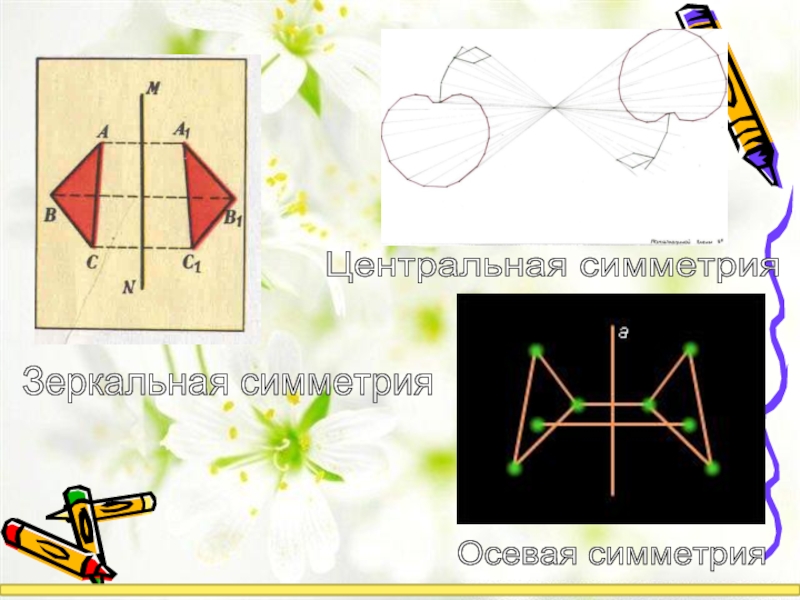
- 3. Виды симметрии а) Лучевая симметрия б) Осевая симметрия в) Центральная симметрия г) Зеркальная симметрия
- 4. Зеркальная симметрия Центральная симметрия Осевая симметрия
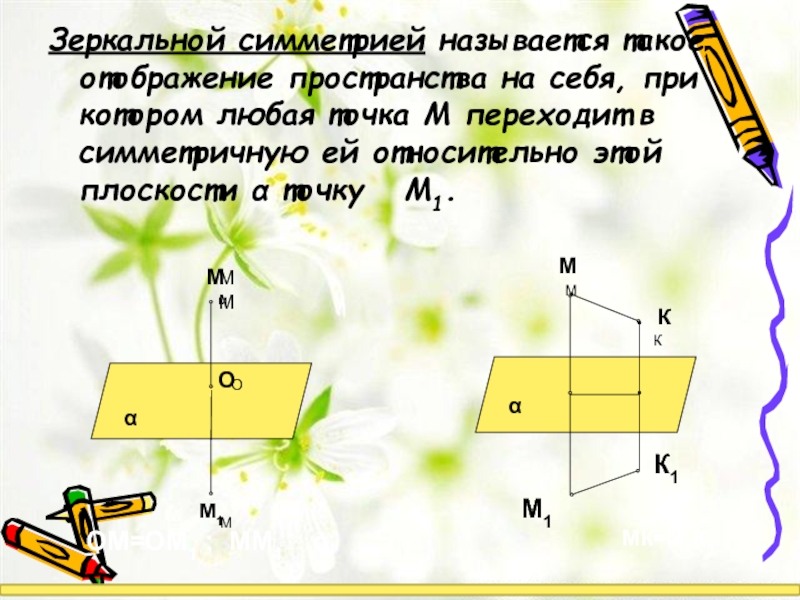
- 5. Зеркальной симметрией называется такое отображение пространства
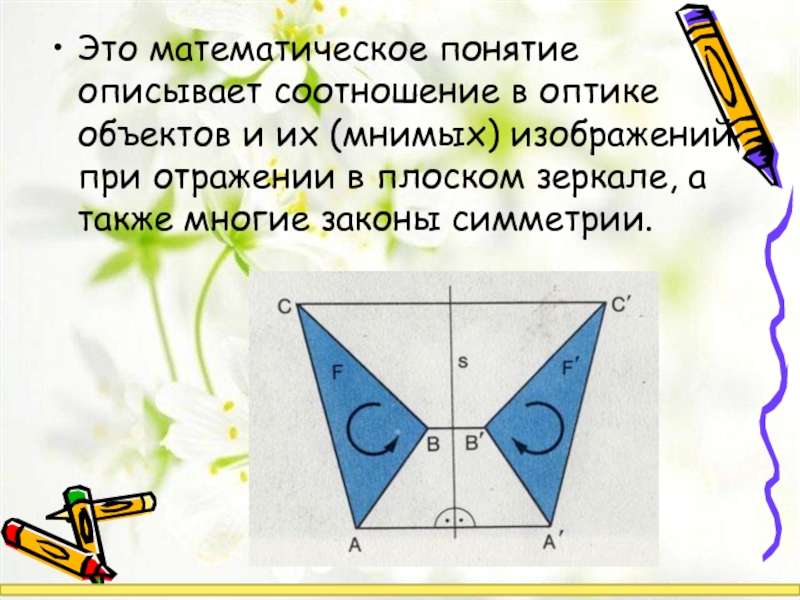
- 6. Это математическое понятие описывает соотношение в
- 7. Геометрическая фигура называется симметричной относительно плоскости S ( рис.104 ), если для
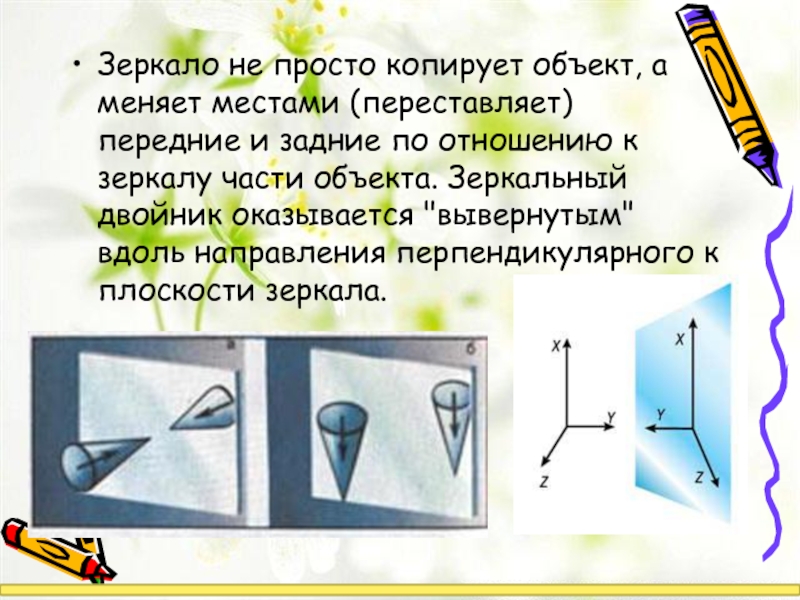
- 8. Зеркало не просто копирует объект, а
- 9. Докажем,что зеркальная симметрия есть движение. Введем прямоугольную
- 10. Если М не лежит в плоскости
- 11. Зеркально осевая симметрия. Если плоская фигура ABCDE ( рис.107
- 12. Многогранник, обладающий зеркально-осевой симметрией; прямая AB — зеркально-поворотная ось.
- 13. Прямая призма обладает зеркальной симметрией. Плоскость симметрии параллельна
- 14. Каждая деталь в симметричной системе существует
- 15. Зеркальная симметрия-это симметрия окружающего нас мира.
- 16. Зеркальная симметрия в природе
- 17. Спасибо за внимание! Десу, ня.
Слайд 1 Зеркальная симметрия
Работу выполнили ученики 11А класса
Константин Фонарь
Слайд 2
Симметрия - это гармония в расположении одинаковых предметов какой-либо группы или частей в
Слайд 3
Виды симметрии
а) Лучевая симметрия
б) Осевая симметрия
в) Центральная симметрия
г) Зеркальная симметрия
Слайд 5
Зеркальной симметрией называется такое отображение пространства на себя, при котором любая
ММ
м
М
М
М1
О
О
М
М
К
К
α
α
ОМ=ОМ1 ; ММ1⊥ α
МК=М1К1
М1
К1
Слайд 6
Это математическое понятие описывает соотношение в оптике объектов и их (мнимых)
Слайд 7
Геометрическая фигура называется симметричной относительно плоскости S ( рис.104 ), если для каждой точки E этой фигуры может быть найдена
Слайд 8
Зеркало не просто копирует объект, а меняет местами (переставляет) передние и
Слайд 9
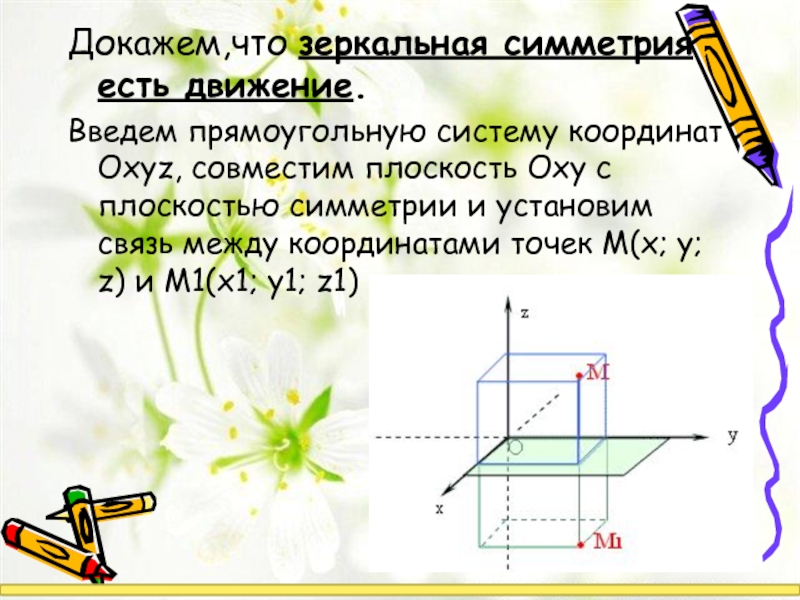
Докажем,что зеркальная симметрия есть движение.
Введем прямоугольную систему координат Оxyz, совместим плоскость Оxy
Слайд 10
Если М не лежит в плоскости Оху, то х =х1, у
Если М I Оху , то x=x1, y=y1, z=z1=0
Рассмотрим А(x1; y1; z1), В(x2; y2; z2), А—> А1, В—> В1 , тогда А1(x1; y1; -z1), В1(x2; y2; -z2), тогда
АВ=А1В1, т.е.Оху – движение.
Слайд 11
Зеркально осевая симметрия.
Если плоская фигура ABCDE ( рис.107 ) симметрична относительно плоскости S
( что возможно, если только
по которой эти плоскости пересекаются, являетсяосью симметрии фигуры ABCDE. В этом случае фигура ABCDE называетсязеркально-симметричной.
Слайд 12
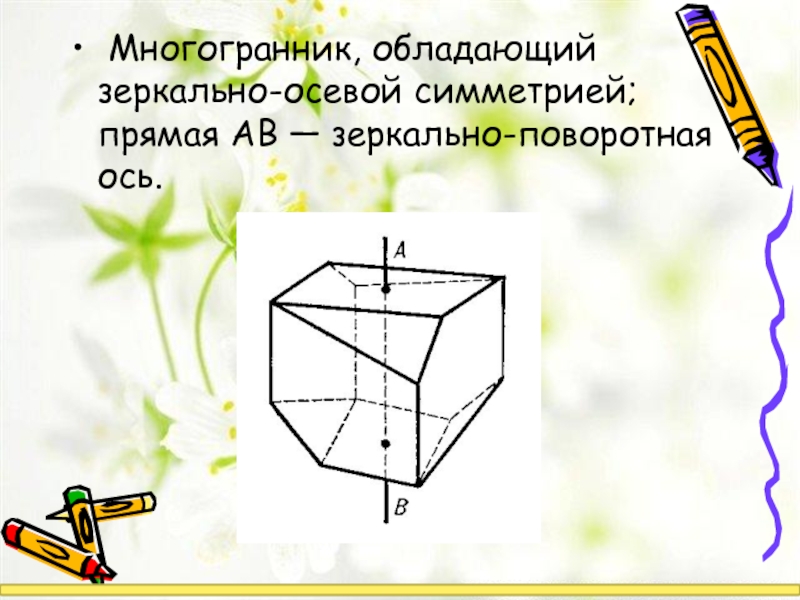
Многогранник, обладающий зеркально-осевой симметрией; прямая AB — зеркально-поворотная ось.
Слайд 13
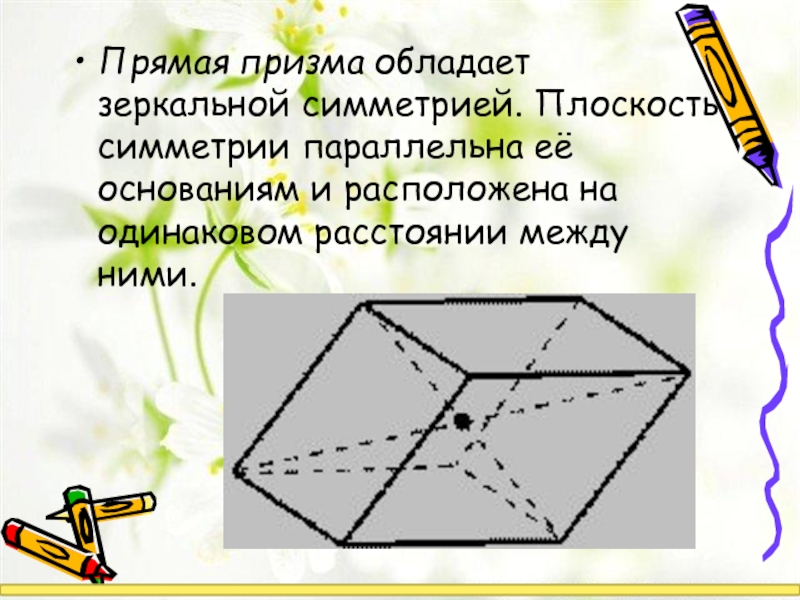
Прямая призма обладает зеркальной симметрией. Плоскость симметрии параллельна её основаниям и расположена на
Слайд 14 Каждая деталь в симметричной системе существует как двойник своей обязательной
Слайд 15
Зеркальная симметрия-это симметрия окружающего нас мира. Построение изображения с помощью зеркальной